Evaluation Compressive Sensing Recovery Algorithms in Crypto Steganography System

Published Online October 2016 in MECS

Recent years, data hiding including steganography and watermarking is important due to internet and telecommunication rapid development. There are three main attributes to be observed in a data hiding system known as capacity, imperceptibility, and robustness. The main issue for steganography is capacity where as the main concern for watermarking is robustness [1].

In general, the task of a steganography system is embedding data into a cover image and transferring to the destination without being detected not only by human visual system (HVS) but also by powerful machine vision techniques or steganalysis algorithms. The steganography are performed [2] either in spatial domain [3] or in transformed domain [4], [5].

Cryptography merely obscures the integrity of information so that it does not make sense to anyone except the administrator [6]. A cryptographic algorithm can be classified based on the number of keys used for encryption and decryption [7]. Accordingly, there are two groups of cryptography systems. The first group named symmetric key system uses single key for both sender and the receiver. The second group named public key system or asymmetric key system uses two keys, a public key which everyone knows and a private key that only the recipient knows. Although, the asymmetric key system enables secure communication via insecure channels, the symmetric key system is faster. RSA is an example of asymmetric key encryption system [6], [8].

While steganography and cryptography are both used to ensure data confidentiality, the cryptography focuses on keeping the contents of a message secret and the steganography focuses on keeping the existence of a message secret [6]. So, high security is achieved by using both steganography and cryptography as well [9], i.e. the encrypted message is hiding by steganography [6].

The traditional approach of reconstructing signals or images from measured data follows the well known Shannon sampling theorem [10] which states that the sampling rate must be twice the highest frequency. Recently, the theory of compressive sensing (CS) or sparse representation showed that a signal can be precisely reconstructed from only a small set of measurements if the signal be sparse. Sparsity has a rich history of applications in signal processing problems including de–noising, de– convolution, restoration and in painting [11]- [13]. It has been observed that sparse representation of signals provide very high compression ratios. Hence, it makes sense to exploit sparsity of signals for hiding secret message in steganography.

This ability of sparse representation was considered for encrypting image folding [13], and for image steganography [1]. In [14], it was shown that the CS based encryption does not achieve Shannon’s definition of perfect secrecy, but can provide a computational guarantee of secrecy. In [15], it was demonstrated that the CS based encryption under some circumstances achieves perfect secrecy.

In this paper, we use the compression and encryption data by CS theory. In CS, compression and encryption is achieved by a single linear measurement step. This step is performed by using a measurement matrix, the resultant compressed measurements are encrypted using asymmetric encryption algorithms that generated by RSA algorithm, next level of security to the compressed and encrypted data is provided with the help of steganography. This encrypted and compressed data is embedded in the cover or host image by using the singular value decomposition (SVD) algorithm. The resultant stego image is transmitted through the network. In receiver side, stego image is received and the CS recovery and decryption algorithms are used to get the secret image. In this paper, two groups of CS recovery algorithms (greedy and convex optimization) in terms of PSNR and time consuming are evaluated. The proposed system satisfies the explained conditions in [15] and achieves better results rather than the recent survey in [16]. Furthermore, a secret image greater than a cover image can be hidden and recovered as well.

This paper is organized as follows. Section 2 provides a background of this work including CS and cryptography by RSA and SVD based watermarking. Section 3 explains the proposed method that is crypto steganography based on CS theory. Section 4 gives the experimental results and compares the proposed method with six research papers [16]- [21]. Finally, Section 5 concludes the paper.

• II.    Reviewing CS, RSA, SVD

In general, CS theory requires that the sensed signal to be sparse in a given orthogonal basis and the sensing vectors to be incoherent with this basis. Due to the vast interest in this topic, there exist several review articles on the basics of CS [22]- [26].

• A.    Compressive Sensing (CS) Theory

CS relies on two principles; sparsity and incoherency. A signal is sparse if it only has few nonzero elements, or it is approximately sparse if it has few large elements and other elements are nearly zero. CS theory exploits the fact that many natural signals are sparse and so compressible when they are expressed in the proper basis. For example a Dirac or a Spike is sparse in time domain where as a sinusoid is sparse in frequency domain. The coherence property is defined between the measurement or sensing matrix, Φ , with size m x n , and the basis or sparse basis matrix, Y with size n x n ,

Д(Ф, у) = Vn max |< Ф z, V j >1 (1) 1< z, j < n where Φ is the z–th row of Φ and ψ j refers to the j–th column of ψ . According to CS theory, the matrices Φ and ψ should have maximum incoherency. It was shown that random matrices are largely incoherent with any fixed basis [25]. In this paper, the basis matrix ψ is determined in DCT domain and the measurement matrix Φ is considered a random matrix with normally distributed pseudorandom numbers. Based on the CS theory, any observed vector is written as:

y m x 1   ^Ф m x n ^x n x 1

where x is the true signal that can be written in some basis (like Fourier, wavelet, and DCT) as:

^x n x 1 ^V n x n s n x 1

where s has only k non–zero entries and so called k– sparse. According to (2) and (3), we have, y m x1  Ф mx n V n x n s n x1 Hmx n s n x1

where H named the dictionary. The CS theory states that such a sparse signal s can be reconstructed by taking m≥ (k logⁿ⁄) linear, non–adaptive measurements whenever a random sensing matrix Φ is used. Furthermore, Φ and ψ or H must satisfy the restricted isometric property (RIP) [23]. To support this theory, the sampling rate below Nyquist is considered. Suppose that m >  2 k and Ф has a uniform distribution and satisfies RIP. If there is not any null message in the set of source messages, perfect secrecy will be achieved via CS [15].

For underdetermined problem, with m <<  n , Eq. (4) does not have unique solution. In this case, the sparse recovery algorithms reconstruct the sparsest s by solving the following optimization problem:

minimize || s1 1 subject to y = Hs (5)

where Ц norm, defined as

||х|1 = У |x[n]| . Often the 1n observed vector includes additive noise, so it is modeled as:

^y m x 1   ^H m x n s n x 1 + e m x 1

where e is a stochastic or deterministic error term with bounded energy ||e|^< e and ^2 norm defined as ||x||2 =^ |x[n]|2 . Then, the sparsest s is obtained by solving the following optimization problem, minimize ||s ||1 subject to ||y-Hs ||2< e (7)

So far, different methods named recovery algorithms have been developed for solving the underdetermined or sparse approximation problems which may broadly be grouped into five different categories [27]. The first group includes greedy algorithms such as the matching pursuit, orthogonal matching pursuit (OMP) [28], compressive sampling orthogonal matching pursuit (CoSaMP) [29] and accelerated iterative hard threshold (AIHT) [30]. The second category of approaches are based on convex optimization like the basis pursuit (BP), focal underdetermined system solver (FOCUSS), L1–Magic toolbox [31] and fixed point continuation (FPC) [32]. The third group is based on some statistical parameters such as the maximum a posteriori (MAP) or minimum mean square error (MMSE). Apart from these, the fourth group is based on non–convex optimization and the fifth group is Brute Force [33] which are not popular.

In this paper we survey the first and the second categories i.e. greedy algorithms and convex optimization.

The greedy algorithms include OMP, CoSaMP and AIHT. In convex optimization we use L1–Magic toolbox that consist of minimum energy (ME) that is initial guess from solution for some of algorithms

Secret Image x

Compressive Sensing Measurement

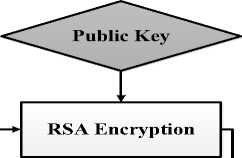
SVD

Stego Image Aw

Cipher Image W

Stego Image Aw*

Cover Image A

(a)

Cipher Image W*

SVD

Secret Image x*

Compressive Sensing Recovery

RSA Decryption

(b)

Fig.1. The block diagram of the proposed method for (a) embedding and (b) extracting.

which require initial value, L1_eq and TV1 that solve equality constrained total variation (TV) minimization, another algorithm that survey in convex optimization group is FPC.

• B.    Cryptography by RSA Algorithm

  The RSA algorithm was proposed in 1977 [6], [8]. The procedures of generating RSA either for public key or private key are written in following [34],

• 1.    Choose two prime numbers, named p and q, then obtain N= pq.

• 2.    Choose a number E, where it is relatively prime to Z= (p-1)(q-1). It means that the greatest common divisor (gcd) of E and Z is 1, i.e. gcd (E, Z)=1 and 1

• 3.    Obtain an integer d as a private key where Ed=1 (mod Z) and mod refers to the remainder of a division.

A message “M” with the public key (N, E) is encrypted and the cipher text “C” is generated as,

C = M^E mod N           (8)

Then at the receiver, the cipher text ' C ' is decrypted by using the known “private key”,

M = C ^d mod N            (9)

The above explained procedures are performed for all pixels of an image. Therefore, the image is encrypted by RSA algorithm.

Lena          Cameraman           Pepper           Airplane           Babon            Barbara            Boat

MRI1          MRI2           MRI3          MRI4          MRI5             MRI6           MRI7

Fig.2. Shown cover images (first row) and the corresponding secret images (second row).

(a)

(b)

Fig.3. Stego images are shown for the sampling rate 34% . (a) the secret image size is the same as the cover image, (b) the secret image size is greater than the cover image.

C. Steganography by SVD Based Watermarking

SVD has been used for different applications such as compression [35], hiding [36], [37], and watermarking [38]. Given a digital image matrix as A with size П х х V n , the SVD of real matrix A is:

A = UE V T =

Г u 11

^u 1 n

^v 11

^V 1 v n

• 1.    Decompose the cover image, A = UE V T .

• 2.    Embed the encrypted and compressed secret image into the diagonal matrix, E^ = E + a W . Where, α is the scale parameter with positive value that controls the strength of the hidden message. It means that we get the convenient stego image quality for the small value of α .

• 3.    Decompose matrix, E^ = U_wE w v W .

• 4.    Obtain the stego image, A_w = UE w V T .

I uTn 1

u Г г

>1 n^n 7

0 к

к ^v A 1   -

v v n v n J

where U and V are orthogonal matrix including the eigen vectors, (.)^T refers to the transpose operation and Σ is the diagonal matrix containing the singular value entries or eigen values in which

^n > 322 > ...> 3rr = ... = ^ > 0     (11)

In general, steganography based on using SVD includes the embedding and the extracting algorithms,

• Embedding

• • Extracting

The extraction algorithm requires U_w , V_w, E and a .

• 1.    Decompose the received stego   image,

• 2.    Obtain matrix, D * = U_w E * Vj .

• 3.    Approximate the encrypted and compressed secret image , W * = 1[D * - E] .

aW = u*eWv*t .

α

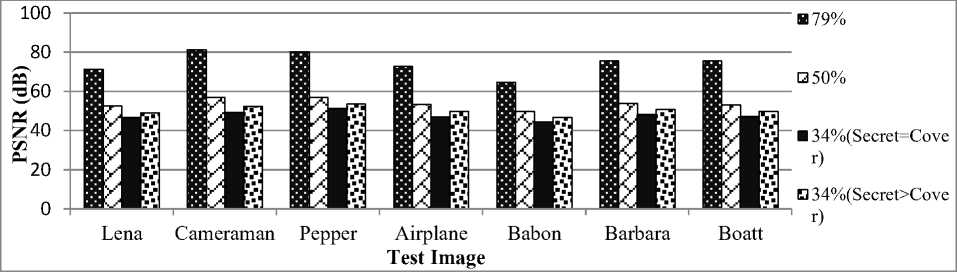
Fig.4. Obtained the PSNRs of 7 stego images for different sampling rates.

(a)

(b)

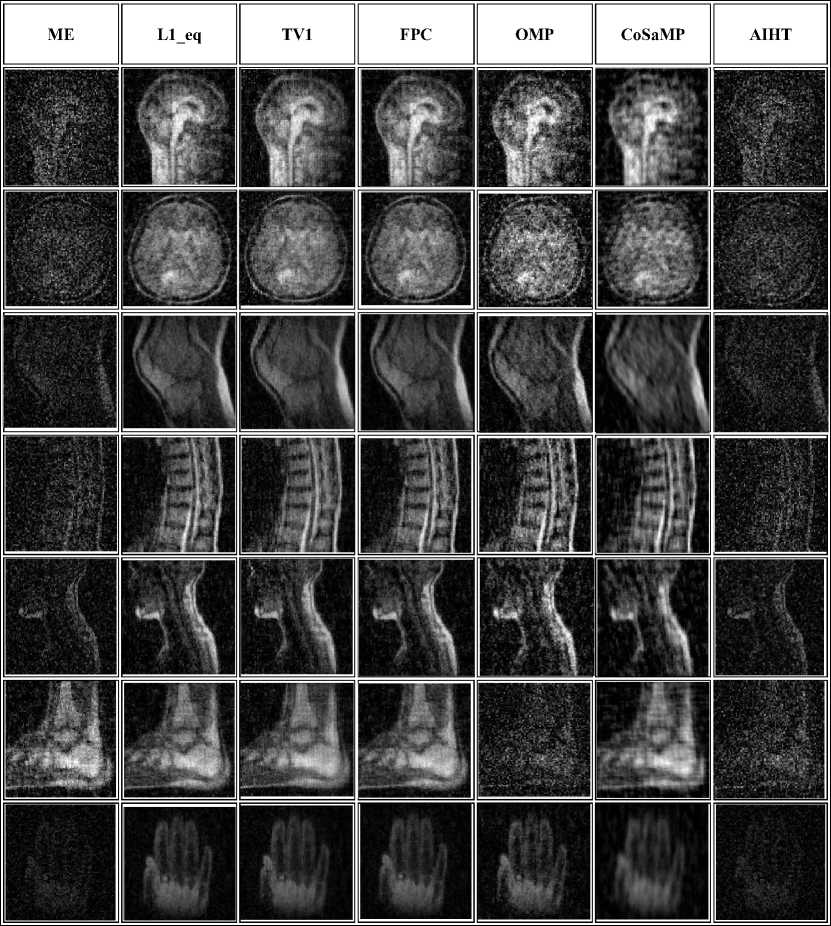
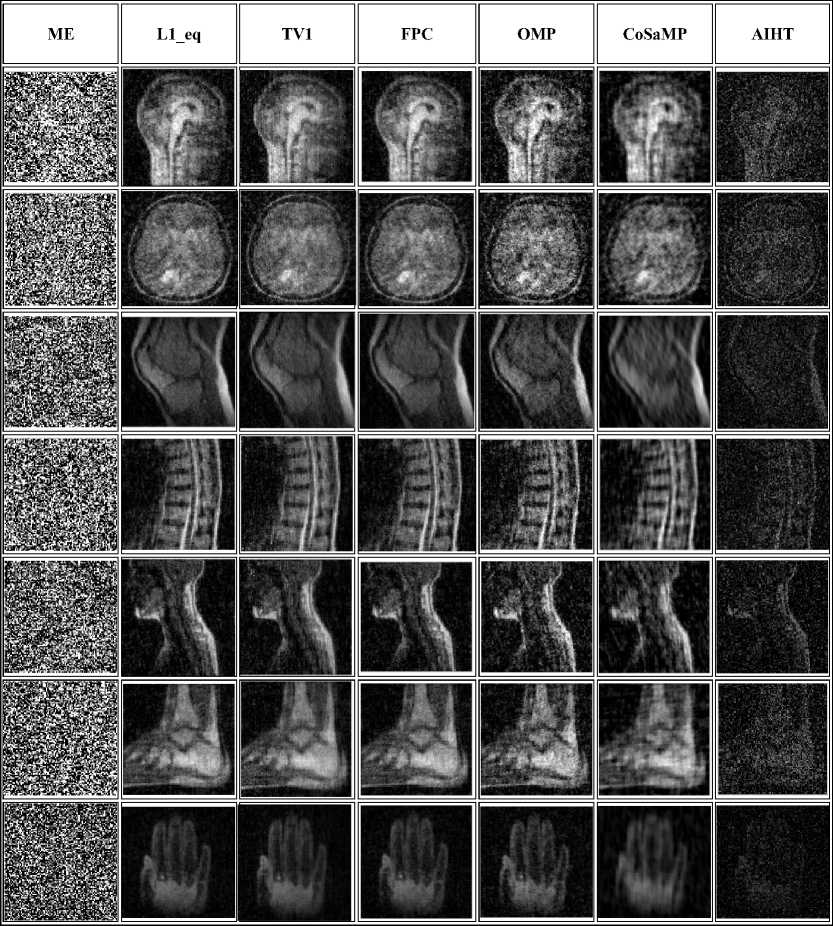
Fig.5. Shown the extracted hidden images by using 7 different CS recovery algorithms (ME, L1_eq, TV1, FPC, OMP, CoSaMP, AIHT) for sampling rates 34%, (a) secret and cover image are the same size, (b) secret image size is greater than cover image.

• III.    The Proposed Method

The block diagram of our proposed method is shown in Fig. 1. As seen in Fig. 1-a, using the CS measurement down size the secret image, ' x' . Therefore, in addition to more security, the system capacity is also increased. These are the main advantages of the proposed method using CS. The observed vector named 'y' is encrypted by RSA algorithm and the cipher image named 'W' is obtained. The cover image is decomposed by using the SVD and the cipher image is embedded. In this paper, according to experiments, the value of α = 10 ^{- 7} . The result image is stego named A

In the receiving stage, seen Fig. 1-b, at first the stego image is decomposed by SVD, the obtained cipher image is decrypted by RSA algorithm and then the secret image is recovered by £_x norm optimization algorithms. In this paper, the private key is used to generate the measurement matrix at the reconstruction stage. So the receiver that knows the correct key, can decrypt the extracted image.

According to [39], any information hiding technique must satisfy the following constraints.

• •    The perceived quality of the cover message should not be degraded due to embed the stego.

• •    The detection of the presence of a hidden message and subsequent determination of the same must require the knowledge of some secret “key”.

  

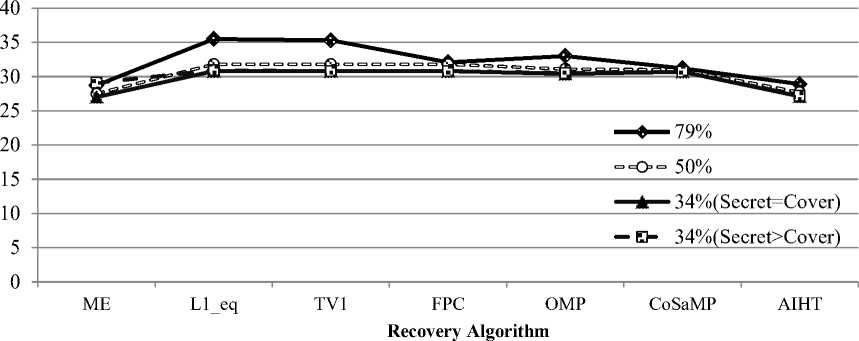
  Fig.6. Comparing the performance of 7 CS recovery algorithms based on average PSNRs.

  
  
  

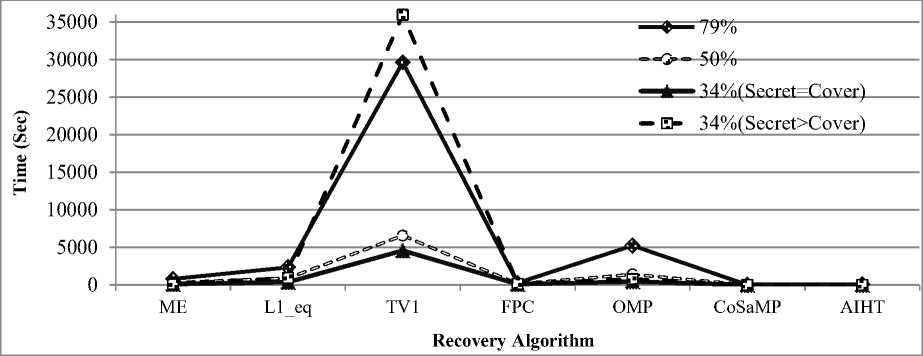
  Fig.7. Comparing the performance of 7 CS recovery algorithms based on average time consuming.

  
  

• •    If multiple messages are hidden within the same cover then they should not interfere.

• •    The hidden message should be robust to the most attacks that do not degrade the perceived quality of the cover message.

Generally, using cryptography and steganography together improve the security of embedded data. This combined chemistry will satisfy constraints in [15] and the requirements such as capacity, security and robustness for secure data transmission over an open channel [6], [8], [34], [40]. In this paper, we show that using CS achieves the appropriate performance, more security and capacity. Furthermore, the secret image size can be even greater than the cover image because of using CS. Accordingly, we get more capacity rather than other crypto steganography systems [16]- [21].

• IV.    Experimental Results

In this paper, as shown in Fig. 2, we choose 7 test images and 7 MRI images as cover and secret images with the same size, i.e. 90×90 pixels. Then in order to show the CS capability of increasing the steganography capacity, the secret image size is considered 101×101 pixels. The method is implemented by using MATLAB R2012b on a PC with CPU 2.20 GHZ 2Duo and RAM 4GB. At first, the secret images with size 90×90 and 101×101 pixels ( x      ) are vectorized into 8100×1, and 10201×1 ( x ), then the observed vector ( y ) is obtained based on Уmxi = Фmxn xnxi. In order to have the different sampling rate, three random entries sensing matrix Φ with size 6400×8100, 4096×8100, and 2809×8100 are generated (the cover and secret are the same size) where the

m sampling rate are defined as x 100 = 79.5,50, and 34%. n

Furthermore, in order to show that the CS increases the steganography capacity and preserves the performance, a sensing matrix Φ with size 3364×10201 is also generated (the secret image size is greater than the cover) where the m sampling rate is x100 = 34%. According to CPU and n

RAM hardware limitation, in this case, we couldn’t have any implementation for sampling rates 50% and 79%. In following the observed vector y is converted into a matrix with size V m x V m pixels and the matrix is encrypted by RSA algorithm. Then, the cipher image named W with size mm x mm pixels is generated.

Table 1. Details of references for comparison with the proposed system.