Evaluation of Performance on Open MP Parallel Platform based on Problem Size
Автор: Yajnaseni Dash, Sanjay Kumar, V.K. Patle
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 6 vol.8, 2016 года.
Бесплатный доступ
This paper evaluates the performance of matrix multiplication algorithm on dual core 2.0 GHz processor with two threads. A novel methodology was designed to implement this algorithm on Open MP platform by selecting time of execution, speed up and efficiency as performance parameters. Based on the experimental analysis, it was found that a good performance can be achieved by executing the problem in parallel rather than sequential after a certain problem size.
Open MP, parallel algorithm, matrix multiplication, performance analysis, speed up, efficiency
Короткий адрес: https://sciup.org/15014874
IDR: 15014874
Текст научной статьи Evaluation of Performance on Open MP Parallel Platform based on Problem Size
Published Online June 2016 in MECS
Parallel computing is the instantaneous utilization of several computer resources for solving a computational problem. The requirement of parallel computing arises to save time/money, to solve complex problems, to do multiple things at a time, to make better use of parallel hardware and to overcome memory constraints. The parallel programs composed of many active processes all at once solving a particular problem by divide and conquer technique. Multi-core processors employ more than one core to solve a problem. The advantage of using multi-core processors is to execute multiple tasks at a time. Performance evaluation is the process of assessing the information of program parameters. One such parameter for measuring the performance of an algorithm is execution time [1][2]. We have applied Open MP (OMP) parallel environment for evaluating the performance of matrix multiplication.
This paper is organized as follows. Section 2 deals with related work done in the current field. Implementation details were presented in section 3. Section 4 focuses on performance evaluation, experimental results and discussion followed by conclusion in section 5.
-
A. Open MP
Open MP stand for open multi-processing. It is the standard programming interface which provides a portable and scalable model for shared memory thread based parallel programming applications. It is an
Application Programming Interface (API) which jointly defined by a group of major computer hardware and software vendors. This API supports C/C++ and FORTRAN on broad variety of platforms including UNIX, LINUX and Windows. The flexibility and easy to use design of Open MP on a supported platform make it as simple as adding some directives to the source code [7][8][9][10][11].
All OMP programs begin as a single process i.e. the master thread. The master thread runs sequentially until the first parallel region construct is encountered. It uses the fork-join model of parallel execution. Here the approach to parallelism is explicit that means programmer has the full control over the parallelization [8][9][10][11]. Figure 1 represents the organization of master and slave threads in the OMP parallel environment.
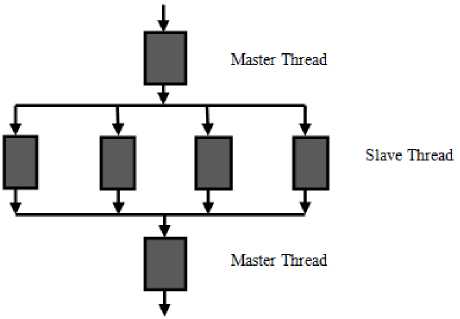
Fig.1. Organization of master and slave threads
-
B. Matrix Multiplication Method
According to an academic research at Berkeley University, USA [12] there were 13 problems important for science and engineering applications. Within these 13 problems was the ‘Dense Linear Algebra’ and it includes matrix multiplication method. Other reasons to choose matrix multiplication are its wide applicability in numerical programming and flexibility of matrix indexing. It is one of the essential parallel algorithms with respect to data locality, cache coherency etc.
[13][14]. The problem of computing the product C = AxB of two large (A and B), dense, matrices was considered.
-
II. Related Work
Parallel computing has gained its popularity since 80’s after the development of supercomputers with massively parallel architectures. There are several parallel computing platforms such as Open MP, Message passing Interface (MPI), Parallel Virtual Machine (PVM), Compute Unified Device Architecture (CUDA), parallel MATLAB etc. In the current study, we have selected OMP parallel environment for evaluating the performance of matrix multiplication algorithm.
Various researches have been carried out to assess the performance of different algorithms in parallel platform since the last decade. Dash et al. provided the overview of optimization techniques applicable for matrix multiplication algorithm [1]. The performance analysis of the matrix multiplication algorithm was studied by using MPI [3]. In a previous study, matrix multiplication problem has also been studied to recognize the effect of problem size on parallelism. But this study was limited to a smaller sample size [4]. Several studies [5][6][7] were carried out for evaluating the performance of matrix multiplication algorithm on multi-core processors by using OMP environment. In similar studies reported in papers [4][5][6][7], where efficiency was not calculated. We have calculated efficiency as one of the performance evaluation parameter. Earlier research was carried out for comparatively on smaller sample sizes. However matrix size up to 5000x5000 was considered for evaluating the performance in the current study.
-
III. Implementation Details
A sequential matrix multiplication algorithm was implemented in OMP and executed in Fedora 17 Linux operating system. The parallel codes have been written using OMP and executed in Intel core2duo processors with dual core for two threads only. The running time of the algorithm on different processors was noted down and the performance measures (speed up, efficiency) of the systems were evaluated accordingly.
-
A. Implementation using multi-core processor
The algorithm was implemented using OMP parallel environment using a multi-core processor. To overcome the limitations of single core processors, which rapidly reach the physical limits of possible complexity and speed, currently multi-core processors are becoming the new industry trend. In view of applicability, a multi-core processor has acquired more than 20% of the new Top 500 supercomputer list [15]. The shifting trend to decrease the size of chips while increasing the number of transistors that they contain has led to enhanced computer performance and reduction in cost. Manufacturers like AMD, IBM, Intel, and Sun have also moved towards production of chips with multiple cooler-running, more energy-efficient processing cores for servers, desktops, and laptops instead of one increasingly powerful core. Though speed factor can be compromised sometimes by use of multi-core chips than single-core models, but adhering to Moore's law they improve overall performance by handling more work in parallel [16]. Program for matrix multiplication was run in following environment. The multi-core processor which was used in this work with hardware descriptions are presented in the Table1 as follows.
Table 1. Multicore Processor with Specifications
|
Components |
Specifications |
|
Model |
Lenovo 3000 G430 |
|
Processor Cores |
Dual core |
|
Processor |
Intel ™ Core2Duo CPU T5800 @ 2.00 GHz |
|
RAM |
3.00 GB (2.87 GB usable) |
|
Operating System |
32-bit OS |
B. Implementation in OMP
Start
Dual Core Processor
Computation of Matrix Multiplication Algorithm
OMP Parallel Programming
Thread 1
*—
Thread 2
---------
Terminate Threads and Display Time Count

Fig.2. Flow graph of OMP module
In our simulation, Fedora 17 Linux operating system with Intel Core2Duo (2.00 GHz) processor was used. On this system, matrix sizes of different orders ranging from 10x10 to 5000x5000 were multiplied without OMP and with OMP. Elements of matrices randomly generated using rand () function and for getting computational time omp_get_wtime () function was used in OMP. In OMP, when time computation is done without using pragma directive, it is called serial time whereas with pragma command it is called parallel time. In this section, all the necessary steps of implementing the algorithm in OMP are described. Figure 2 represents the flow graph of OMP module.
-
C. Matrix multiplication without Open MP
Step 1: Declare variables to store allocated memory
Step 2: Declare variables to input matrix size
Step 3: Declare variable to calculate the time difference between the start and end of the execution.
Step 4: Enter dimension ‘N’ for ‘NxN’ matrix (105000)
Step 5: Allocate dynamic memory for matrix using malloc function.
Step 6: Initialize first and second matrix using randomization method.
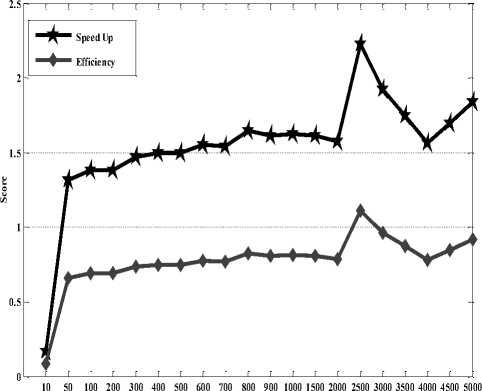
for(i=0; i arr2[i][j] = (rand() % n);} } Step 7: Start the timer. start = omp_get_wtime(); Step 9: Do naive matrix multiplication. for(i=0; i for(k=0; k } arr3[i][j] = temp; } } Step 10: End the timer. end = omp_get_wtime(); Step 11: Calculate the difference in start and end time. Difference = (end – start) / Clocks_Per_Second. Step 12: Print the time required for program execution without OMP. D. Matrix multiplication with Open MP Step 1: Declare variables to store allocated memory Step 2: Declare variables to input matrix size as i, j, k, n and temp. Step 3: Declare variables to be used by Open MP function for finding the number of threads, maximum number of threads and number of processors that can be used in the execution of the program. Another function [omp_in_parallel()] of OMP was also employed to know whether the code execution occurring in parallel or not. This function return 1 if code is in parallel otherwise it returns 0. Step 4: Declare variable to calculate the starting and ending time for computation. Step 5: Enter dimension ‘N’ for ‘NxN’ matrix (105000) Step 6: Allocate dynamic memory for matrix using malloc function. Step 7: Initialize first and second matrix using randomization method. for(i=0; i arr2[i][j] = (rand() % n);} } Step 8: Start the timer. start = omp_get_wtime(); Step 9: The Actual Parallel region starts here #pragma omp parallel for private ( nthreads, tid, maxt, procs, inpar) { /*obtain thread number*/ tid = omp_get_thread_num(); /* only master thread does this */ if (tid==0) { printf ("Threads %d getting environment info...\n", tid); Step 10: Get environment information maxt = omp_get_max_threads(); nthreads = omp_get_num_threads(); procs= omp_get_num_procs(); inpar= omp_in_parallel(); } Step 11: Print environment information printf (“Maximum threads = %d\n”, maxt); printf (“Number of threads = %d\n”, nthreads); printf (“Number of processors = %d\n”, procs); printf (“In parallel? = %d\n”, inpar); } } Step 12: Do naive matrix multiplication using parallel pragma directive of OMP. #pragma omp parallel for private (i, j, k, temp) for(i=0; i for(k=0; k } arr3[i][j] = temp; } } Step 13: End the timer. end = omp_get_wtime(); Step 14: Calculate the difference in start and end time. Difference = (end – start) / Clocks_Per_Second; Step 15: Print the time required for program execution with OMP. IV. Performance Evaluation The performance measures are employed to know the timeliness, efficiency and quality of a particular system. Here two performance measures i.e. speed up and efficiency are used in our study to evaluate the performance of matrix multiplication algorithm in OMP parallel environment. A. Performance Measures Speedup: Speedup is the ratio of the time required to execute a given program sequentially and the time required to execute the same problem in parallel as given in (1). SpeedUp(S) = OMPSequntialTime . OMPParallelTime Efficiency: It is one of the important metric used for performance measurement of parallel computer system. Efficiency metric is applied to find out how the resources of the parallel systems are being utilized. This is also called as degree of effectiveness. Here in this study, the numbers of processors are 2 as dual core systems have been used. The formula is given in (2). OMPSpeedUp Efficiency(E) = . (2) B. OMP Execution Time Results Computational execution times including both sequential and parallel run were recorded in Open MP parallel programming environment. These results were shown in Table 2 and a graph was plotted accordingly in Figure 3. Table 2. Execution Time of OMP Matrix size Sequential time Parallel time 10x10 0.000046 0.000273 50x50 0.001535 0.001167 100x100 0.01327 0.009603 200x200 0.029811 0.021555 300x300 0.335226 0.228125 400x400 1.000831 0.667475 500x500 2.127931 1.421125 600x600 3.94911 2.539687 700x700 6.070147 3.931948 800x800 10.625654 6.459272 900x900 15.43963 9.550435 1000x1000 21.336303 13.137191 1500x1500 112.655111 69.802859 2000x2000 177.362122 112.565785 2500x2500 418.590416 188.201826 3000x3000 574.658692 298.450969 3500x3500 812.505873 465.223017 4000x4000 1328.852847 850.408619 4500x4500 1770.902282 1042.201657 5000x5000 2213.815603 1203.885703 Table2 illustrates the comparison of both the sequential and parallel time of the matrix multiplication algorithm. The highest sequential time required to execute 5000x5000 matrix sizes is 2213.815603 seconds whereas it has taken only 1203.885703 seconds for parallel execution using OMP. Matrix Size Fig.3. Execution time of OMP C. OMP Performance Results Speed up and efficiency measures were calculated to analyse the performance of matrix multiplication algorithm in Open MP programming platform. These results were presented in Table 3 and Figure 4. Table 3. Performance Metrics Results for OMP Matrix size Speed up Efficiency 10x10 0.168498168 0.084249084 50x50 1.315338475 0.657669237 100x100 1.381859835 0.690929918 200x200 1.383020181 0.69151009 300x300 1.469483836 0.734741918 400x400 1.499428443 0.749714222 500x500 1.497356672 0.748678336 600x600 1.554959332 0.777479666 700x700 1.543801444 0.771900722 800x800 1.645023464 0.822511732 900x900 1.616641546 0.808320773 1000x1000 1.624114546 0.812057273 1500x1500 1.613903966 0.806951983 2000x2000 1.575630837 0.787815418 2500x2500 2.224157039 1.112078519 3000x3000 1.925471021 0.962735511 3500x3500 1.746486832 0.873243416 4000x4000 1.562605102 0.781302551 4500x4500 1.699193501 0.84959675 5000x5000 1.838891846 0.919445923 D. Discussion A dataset of 10x10, 50x50, 100x100, 200x200, …., up to 5000x5000 was considered for performance evaluation purpose. It was observed from the study, that in OMP, the time required for the sequential execution of multiplication of 10x10 matrix size was less as compared to the parallel execution time. However, the parallel execution gives better result from 50x50 size matrix onwards. This signifies that the size of problem also matters in achieving better parallelism. The small problem size leads to a parallel slowdown phenomenon, which results from the communication bottleneck. This means parallelism should be adopted beyond a certain size of problem only [4]. In current case for OMP and 2.00 GHz processor, parallelism is effective only after 50x50 matrix multiplication. Thus, effective parallelism can be achieved after 50x50 matrix size in OMP. It was also observed that speed up and efficiency both increase slowly with matrix size (problem size). From this study it has been found that ^ 1) ST < PT (for below 50x50 matrix size) 2) ST > PT (for above 50x50 matrix size) Here, ST denotes sequential time and PT denotes parallel time. Matrix Size Fig.4. Performance of OMP V. Conclusion OMP is a great tool for parallel computing environment having richness of functionalities. In this study, it was observed that the parallel algorithm cannot perform better than sequential algorithm when data set size is small. However, as we increase the size of the data set the execution of parallel algorithm starts performing better and provides much better outcomes than the sequential execution.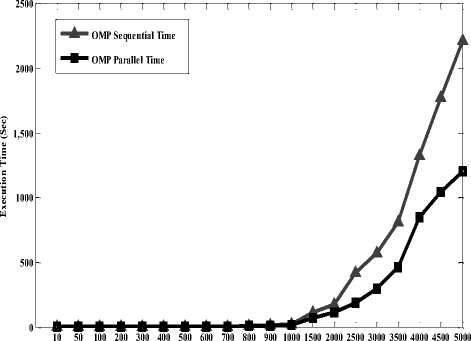
Список литературы Evaluation of Performance on Open MP Parallel Platform based on Problem Size
- Y. Dash, S. Kumar, V.K Patle. , "A Survey on Serial and Parallel Optimization Techniques Applicable for Matrix Multiplication Algorithm," American Journal of Computer Science and Engineering Survey (AJCSES), vol 3, issue 1, Feb 2015.
- K. Hwang, N. Jotwani, "Advanced Computer Architecture", Tata McGraw Hill education Private Limited, Second Edition, 2001.
- J. Ali, R.Z. Khan, "Performance Analysis of Matrix Multiplication Algorithms Using MPI," International Journal of Computer Science and Information Technologies (IJCSIT), vol. 3 (1), pp. 3103 -3106, 2012.
- R. Patel, S. Kumar, "Effect of problem size on parallelism", Proc. of 2nd International conference on Biomedical Engineering & Assistive Technologies at NIT Jalandhar, pp. 418-420, 2012.
- S.K. Sharma, K. Gupta, "Performance Analysis of Parallel Algorithms on Multi-core System using OpenMP Programming Approaches", International Journal of Computer Science, Engineering and Information Technology (IJCSEIT), vol.2, No.5, 2012.
- S. Kathavate, N.K. Srinath, "Efficiency of Parallel Algorithms on Multi Core Systems Using OpenMP," International Journal of Advanced Research in Computer and Communication Engineering, Vol. 3, Issue 10, pp. 8237-8241, October 2014..
- P. Kulkarni, S. Pathare, "Performance analysis of parallel algorithm over sequential using OpenMP," IOSR Journal of Computer Engineering (IOSR-JCE), Volume 16, Issue 2, pp. 58-62.
- P. Graham, "OpenMP: A Parallel Programming Model for Shared Memory Architectures," Edinburgh Parallel Computing Centre, The University of Edinburgh, Version 1.1, March 1999.
- M. J. Quinn, " Parallel Programming in C with MPI and OpenMP," McGraw Hill, 1st edition, 2004
- Uusheikh, "Begin Parallel Programming with OpenMP" CPOL Malaysia 5 Jun 2007.
- OpenMP: https://computing.llnl.gov/tutorials/openMP/.
- K. Asanovic, R. Bodik, B. Catanzaro et al., "The landscape of parallel computing research: A view from Berkeley," Technical Report UCB/EECS-2006-183, EECS Department, University of California, Berkeley, December 2006.
- K. Thouti, S.R. Sathe, "Comparison of OpenMP and OpenCL Parallel processing Technologies", UACSA, vol. 3, issue 4, pp. 56-61, 2012.
- R. Choy, A. Edelman, "Parallel MATLAB: Doing it Right," Computer Science AI Laboratory, Massachusetts Institute of Technology, Cambridge, MA 02139.
- L.Chai, "Understanding the Impact of Multi-Core Architecture in Cluster Computing: A Case Study with Intel Dual-Core System," Seventh IEEE International Symposium on Cluster Computing and the Grid, pp 471-478, 14-17 May 2007.
- D. Geer, "Chip makers turn to multicore processors," Computer, IEEE Explore, Vol.38, May 2005, pp 11-13.


