Evaluation of the dynamics of elastic plate and liquid section dynamic absorber
Автор: Mirsaidov M.M., Dusmatov O.M., Khodjabekov M.U.
Статья в выпуске: 3, 2022 года.
Бесплатный доступ
In this paper, the problem of studying the dynamics of transverse vibrations of plate, taking into account the elastic dissipative characteristics of the hysteresis type in conjunction with a liquid section dynamic absorber under the influence of kinematic excitations. In the differential equations of motion, the elastic dissipative characteristics of the plate material of the hysteresis type are taken into account by means of harmonic linearization coefficients based on the Pisarenko - Boginich hypothesis. The amplitude-frequency characteristic of the vibrating plate and the analytical expressions of the transfer function were determined using a differential operator from a system of differential equations of motion depending on the system parameters. In order to perform numerical calculations, the coefficients of the first three terms of the logarithmic decrement expression were found. In the amplitude interval, the function representing the vertical deviation of the amplitude-frequency characteristic decreases and the function representing the energy dissipation in the plate material increases. It has been shown that the efficiency of the liquid section dynamic absorber in quenching harmful plate vibrations at low frequencies can be evaluated based on the results of numerical calculations to ensure that the displacements of the plate point reach minimum values. Amplitude-frequency characteristics for plate points at different parameters were constructed for the distributed parametric system using the developed model and method. Recommendations for the selection of parameters of the system depending on the elastic dissipative and inertial properties are given.
Plate, liquid section dynamic absorber, hysteresis, vibration, vibration protection, logarithmic decrement, amplitude-frequency characteristic, transfer function, frequency, dynamics
Короткий адрес: https://sciup.org/146282551
IDR: 146282551 | УДК: 531: | DOI: 10.15593/perm.mech/2022.3.06
Текст научной статьи Evaluation of the dynamics of elastic plate and liquid section dynamic absorber
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2022PNRPU MECHANICS BULLETIN
The problem of protection of mechanical systems under the influence of various excitations used in modern techniques, technologies, mechanisms and their elements from harmful vibrations, taking into account their nonlinear characteristics, is one of the most urgent problems that need to be solved. So far, a lot of theoretical and experimental research has been done in this regard. However, there is a need to make important recommendations and research methods to protect mechanical systems, especially plates, from low-frequency harmful vibrations, taking into account the elastic dissipative characteristics of the hysteresis type, ie the use of liquid section dynamic absorber.
The work [1] studied the transverse vibrations of the hysteresis type elastic dissipative characteristic wire stretched along the length of the plate and its upper surface under the influence of multigarmonic excitations. The effectiveness of the wire in quenching plate vibrations is shown by the results obtained based on the analysis of the energy dissipation factor of the system. Numerical analyzes have shown that the vibration amplitudes are directly proportional to the energy distribution factor of the system. Aluminum, steel and rubbers were selected for the wire material and their effectiveness in quenching vibrations at low frequencies was compared.
The finite element method was used in the work [2] to solve the problem of plate vibrations. In this case, it is shown that the averaged equations of the energy equations with respect to time and coordinate represent the nature of the vibrations. It is shown that these equations can also be used to calculate the energies of complex systems in their vibrations. Expressions of plate energy distribution factors and external power frequencies were also determined and compared with the results obtained by other methods, revealing the reliability of the results.
In the works [3; 4], the vibrations of the rectangular plate with the edges mounted on elastic springs were studied using approaching rows. The natural frequency was determined depending on the system parameters and quantified. The analytical expression of the mode shapes satisfying the boundary conditions is proposed in a new form, i.e., in the form of the addition of additional polynomials to the Fury series. Mode shapes were analyzed numerically and the effect of system parameters on their change was evaluated as a result of numerical calculations.
The work [5] deals with the determination of analytical expressions of mode shapes and natural frequencies in the transverse vibrations of the plate. The method of integral substitutions was used. The plate base was taken as the Winkler elastic base, and the analytical expressions of the mode shapes and natural frequencies of the plate lying in the free tanks were analyzed numerically. It has been noted that energy methods are effective in determining natural frequencies. Recommendations are given for the identification of mode shapes that meet the boundary conditions.
The work [6] deals with the vibrations and stability of the layer of rectangular plates. In this case, several layers of plates are connected by a linear elastic characteristic. The natural frequency and the critical forces in bending are analytically expressed. The expression for the natural frequency depends on the number of plate layers is taken. Explored the stability and the geometric dimensions of the layers were analyzed at different values of stiffness. The practical significance of the results and the application of the obtained equations in engineering practice are shown.
The work [7] studies the vibrations and the stability of the plate moving along an axis along its length. The partial derivative differential equations of motion are determined using the moment expressions. Natural frequencies were found using both the Galerkin and differential quadrature methods. If the velocity of motion along the axis does not change, the boundaries of instability are determined and their change is analyzed, provided that the real part of the roots of the characteristic equation is positive. The minimum of unstable areas is determined depending on the system parameters.
The work [8] studies parametric vibrations and stability of complex shaped plates under the influence of static and periodic forces. Variational methods were used in the analysis of motion equations. The geometric parameters, boundary conditions, and the effect of the applied rectangular plate on the geometric center of the applied external forces on the domain are analyzed. In particular, an increase in the ratio of the side of the square hole to the smaller side of the plate has led to a decrease in the areas of instability.
The work [9] presents an effective method for studying the vibrations of the plate moving along an axis along its length in a liquid. This method was developed using Kirchhoff’s theory and finite difference methods. In this case, the fluid is considered to be an ideal fluid and its equations are derived in the form of Bernoulli equations. The Hamiltonian principle was used to obtain the equations of motion of a plate in a liquid. It has been shown that an increase in the density of the liquid or the depth at which the plate is immersed in the liquid leads to a decrease in the natural frequency.
The work [10] is devoted to defining the instability borders of plate motion. In this case, the equations of motion and boundary conditions are determined using the Hamiltonian principle. Analytical expressions of the boundaries of instability were derived from the Hurwitz criterion and the effect of damping coefficients on the areas of instability was investigated. The differential quadrature method was used to perform numerical calculations. Stability borders in the first four natural frequency and mode shapes were analyzed and conclusions were drawn.
The works [11–13] deal with the problem of structural modeling of distributed systems with linear elastic characteristics by the method of bond graph. The equations of motion are expressed by first-order derivatives, and the stability of motion explored from the system matrix. The vibration frequency ranges corresponding to the largest amplitudes are shown. Nonlinear free and forced vibrations of discrete and continuous systems have also been studied. The systems are mathematically modeled using the Lagrange equation.
In the work [14], the transverse vibrations of the plate in conjunction with the dynamic absorber were investigated using finite difference method. The lumped mass was obtained as a dynamic absorber. Placing a single lumped mass in the center of the plate as a dynamic absorber has been shown to be effective only at a certain frequency. It is necessary to install several masses in different parts of the plate in order to reduce the vibrations of the plate over a wide range of frequencies. The optimal value of the set mass is determined. In this case, the product of mass density, surface area, height is obtained, and the optimal values for surfaces and heights are given.
The work [15] deals with the problem of quenching the vibrations of right-angled, isotropic and orthotropic plates, which are protected from vibrations by fixed at the ends. As objects to protect against vibrations, in the first case, one mass is installed in the geometric center of the plate, in the second case, a total of four masses, one in the middle of the sides. In this case, the Reyleigh-Ritz method was used to determine the natural frequencies that satisfy the boundary conditions. The change in frequencies with the change in the aspect ratio was quantified. A methodology for determining mode shapes that satisfies boundary conditions has been developed.
The work [16] presents methods for determining the natural vibration frequencies of the rectangular plate attached to an elastic base by experiment. In this case, 6061-T6 aluminum was obtained for the plate material. The frequency values determined experimentally were compared with the results obtained according to Kirchhoff – Love theory and the reliability of the results was shown. It is revealed that the given frequency expression is effective in determining the natural frequencies of isotropic plates.
In the work [17], the natural frequencies, masses, and stiffness matrices of an isotropic thin plate were determined by the finite difference method. The obtained frequencies were compared with the analytical solutions of the frequencies obtained when the mode shapes were obtained in the Levi type. The results obtained show that it is identical to its analytical solution for the plate with a free boundary condition. In this case, it was found that the change in plate thickness had no effect on the change in frequency.
In the work [18], the transverse vibrations of the plate with a circular hole in the center were studied. The natural frequencies were determined by the Reyleigh – Ritz method. The characteristics of the hole are expressed by the Bessel function and the effect of vibration reduction is evaluated. The change in natural frequency with increasing diameter was analyzed under different boundary conditions and the optimal parameter for the radius was determined.
The work [19] examines the damping properties of a passive liquid section dynamic absorber, which is effective in quenching harmful vibrations of engineering systems. The problem of optimization to minimize the amplitude of vibration over a wide range of frequencies, taking into account the maximum rise limit of the fluid in the columns, was considered and solved using numerical methods.
The works [20; 21] focus on the optimal design of liquid section dynamic absorber to control the seismic impact of structures. Algorithms were used in the optimization process to achieve the optimal solution.
In the works [22; 23], several types of liquid section dynamic absorbers were compared. The impact properties of liquid section dynamic absorbers on the object have been shown to be modified by the application of their different shapes, the installation of additional barriers inside the shell surrounding the water, and the application of different types of fluid.
The works [24; 25] have shown that semi-active systems cover the properties of passive and active systems. A passive liquid section dynamic absorber converted to a semi-active system with variable damping properties was analyzed.
The work [26] analyzes the effect of a liquid section dynamic absorber on the motion of nonlinear systems under the influence of narrow and wide-band random excitations. The hysteresis type elastic dissipative properties of the system are based on the Bouc – Wen model. The equivalent statistical linearization method was used to analyze the dynamic nature of the system. The results showed that setting the liquid section dynamic absorber switch at frequencies close to the frequency of the system at wide-band random vibrations, and at frequencies with a high probability of external force vibrations at narrow-band random vibrations would be optimal values for its efficiency.
In the work [27], the liquid section dynamic absorber was used to quench low-frequency vibrations of the drilling platform. Initially, the equation of joint motion of liquid section dynamic absorber and the drilling platform was obtained and analyzed using numerical methods. In the rotational motion of the drilling platform, its interaction with the liquid section dynamic absorber was evaluated and the torsional vibrations in the rotational motion of the drilling platform at low frequencies were quenched.
In the work [28], a liquid section dynamic absorber was used as a new energy-absorbing mechanism to quench the horizontal vibrations caused by external influences in the vertical flat rotational motions of the underwater platform.
The use of liquid section dynamic absorber to protect structures from harmful vibrations has been studied in [29]. The statistical linearization method was used for random processes. The standard deviation values are expressed analytically depending on the system parameters
The works [30–32] study the dynamics of complex mechanical systems and the bending of systems consisting of several layers of distributed parameters.
A mathematical model of transverse vibrations under the influence of harmonic and random excitations of a plate with elastic dissipative characteristics of the hysteresis type, protected from vibrations, is presented and studied in [33]. The
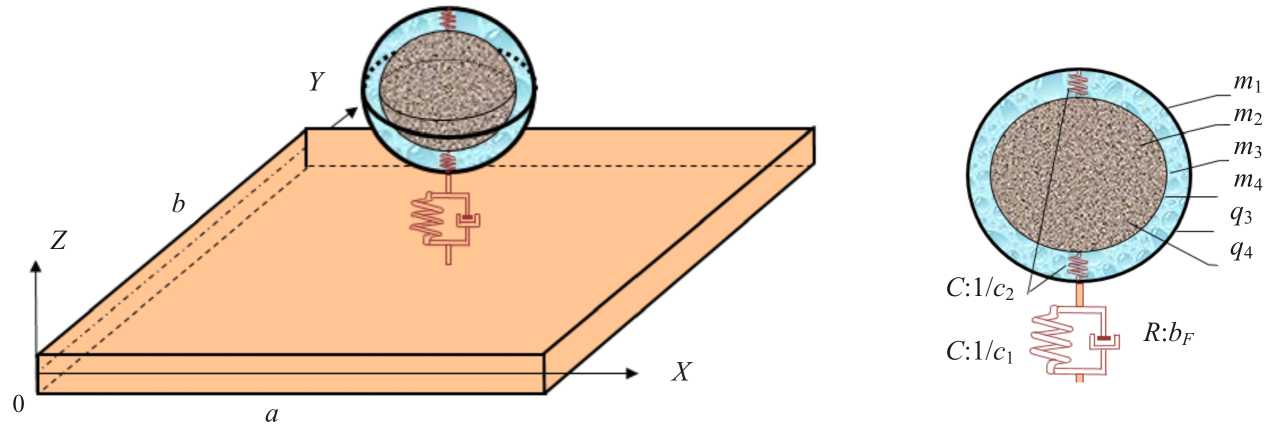
Fig. 1. Scheme of plate and liquid section dynamic absorbing system
elastic characteristics of the hysteresis type of the plate material are obtained on the basis of the Pisarenko – Boginich hypothesis. Quantitative calculations were performed and analyzed on the obtained results, conclusions were drawn and recommendations were developed.
In the works [34; 35], the mathematical model of transverse vibrations of systems of elastic dissipative characteristic of hysteresis type protected from vibrations is given and explored the stability. In this case, a conventional dynamic absorber is taken as an object that protects the plate from harmful vibrations.
In the work [36] considered the problem of determining the mode shapes of liquid section dynamic absorber when it is used as an object to quench the vibrations.
The analysis of the above works shows that one of the most important problems of mechanics is the solution of low-frequency vibrations in plates with elastic dissipative characteristics of the hysteresis type under the influence of kinematic excitations.
This work is devoted to solving the problem of studying the dynamics of nonlinear transverse vibrations of the plate in conjunction with the liquid section dynamic absorber under the influence of kinematic excitations.
1. Materials and methods
Under the influence of kinematic excitations, elastic dissipative characteristic of hysteresis type rectangular plate with sides a , b , and thickness h vibrates in conjunction with a liquid section dynamic absorber (Fig. 1): m 1 and q 3 are the mass and displacement of the outer body of the dynamic absorber surrounding the liquid, respectively; m 2 and q 4 are the mass and displacement of the solid of the dynamic absorber, respectively; m 3 is mass of the liquid; m 4 is mass of the liquid adhering to the body with mass m 2 ; bF is the coefficient of resistance of the damper; c 1 and c 2 are stiffness coefficients.
When the kinematic excitations consist of forces F L ( t ) = F L and F R ( t ) = F R placed between the opposite
sides of the plate, the motion of the elastic dissipative characteristic plate of the hysteresis type protected from the vibrations under consideration can be mathematically modeled as follows:
■ • ■
AQ + BQ + CQ = F ,
where
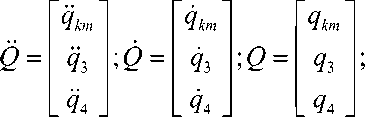
u km 0 FL
F.
kma R
F =
m km
( ml * + m 2 ) u km 1 ( m 2 - mv ) u m i
0 0
m13 * + m 2 m 2 + m v ;
m 2 - m v m 2 + m 4
|
" 0 |
- u km 1 b F |
0 " |
" C km |
- Ukm 1 c 1 |
0 " |
||
|
B = |
0 |
bF |
0 |
; C = |
0 |
c 1 |
0 |
|
_ 0 |
0 |
b s _ |
_ 0 |
0 |
2 c 2 |
q km are displacements of plate points; m 13 * = m 1 + m 3 ; m v is mass of the liquid squeezed by the solid with mass m 2 ; bS is the viscosity coefficient of the liquid; mkm and сkm are modal masses and stiffnesses, expressed as ( k , m = 1... n ):
a b mkm = Я Phukmdxdy;
0 0
c km
a b
( 1 + D 0 ( —П 1 + j П 2 ) )Я P hu km dxdy
0 0
3 Ds 1
+ — (-П1 + jП2 )EDR^kma tokm R=1
hR
2R (R + 3)
+
a b 2 2
Я U km [ (( ^^ km +
I о о d x d x
8 2 Urn + Ц n—km дy
д 2 u km , д2 u km д x2 + ц n д y2
\ д 2 /д 2 н^ д 2 u^ )
) + ~ ( -^T + Ц n^4m I х д y | д y д x )
2. Results and discussion
8 2 Ukm
-km +ц д У
n
^ Um
R 6 D s 2
)] dxdy + — ( 1 - Ц n ) (V 1 - j v 2 ) £ KN q m, x
» km N = 1
hN
x ——----
2 N ( N + 3 )
a b
∬ u
0 0
, д2
km дx дy
| 8 u km
8 2 u km
д x д y ) д x д y
N )
dxdy +
In order to determine the amplitude-frequency characteristic of the transverse vibrations of the plate with an elastic dissipative characteristic of the hysteresis type in conjunction with the liquid section dynamic absorber under the influence of kinematic excitations, we solve the system of equations (2) on the basis of Kramer's rule.
2 D
+77”( 1 -ц n )x W.
km
q ( S ) = b 3 ( b b 9 - b 6 b ) .
km Ь 1 ( Ь 5 Ь 9 - Ь 6 Ь 8 ) + Ь 2 ( Ь 6 Ь 7 - Ь 4 Ь 9 ) ’
a b д 4 и
X ( V 1 - j V 2 ) K0 $ u km я -m dxdy ] ® 2 m '; 00 д x д y
q 3 ( s ) = —b ’ ( b 6 Ь 7 - b 4 b 9 ) ------;;
Ь 1 ( Ь 5 Ь 9 - Ь 6 Ь 8 ) + Ь 2 ( Ь 6 Ь 7 - Ь 4 b 9 )
p is density of the plate material; U m = U m ( x , y ) are mode shapes; D 0, D 1,..., D R , K 0, K 1,..., KN are parameters
Eh 3
determined experimentally [37]; D = —- ------ - is a cylin-
12 ( 1 -Ц )
drical stiffness; E is Young’s module; ц n is Poisson's coeffi
q 4 ( S ) = b^--- ;
Ь 1 ( Ь 5 Ь 9 - Ь 6 Ь 8 ) + Ь 2 ( Ь 6 Ь 7 - Ь 4 b 9 )
where
cient; qkma are amplitude values of plate vibration forms; ® km are natural frequencies of the plate; n 1 , П 2 = П 22 sign ( ® ) , v 1 , v 2 = v 22 sign ( ® ) are constant coefficients depending on the dissipative properties of the plate material and are determined experimentally [33]; ® is a system frequency; j 2 = - 1 ;
f x f x )
u km 0 = Um I 2,0 l , u mb = Um I 2, b l and Um 1 = Um ( x 1 , y 1 ) are the values of the mode shapes at the points where the forces are applied and at the point where the liquid section dynamic absorber is installed.
In order to determine the amplitude-frequency characteristic of the system under consideration, we write the system of differential equations (1) as a system of algebraic equations by the differential operator S = d -, ie
( m kmS 2 + c km ) q km - Um 1 ( bFS + C 1 ) q 3 = u km 0 FL + UkmbFR ;
M 1 Uk m 1 S 2 q km + ( M 1 S 2 + b F S + C 1 ) q 3 + m 2 s 2 q 4 = 0; (2)
M 3 Ukm 1S2 qkm + M 3 S2 q3 +(M 4 S2 + bsS + 2 c 2) q 4 = 0, where
M 1 = m 13 * + m 2; M 2 = m 2 + m v ; M 3 = m 2 - m v ; M 4 = m 2 + m 4.
The obtained system of equations (2) is a system of linear equations with respect to the variables qkm , q 3, q 4. This allows us to solve this system of equations with respect to these variables. Given that the absolute values of the variables qkm , q 3, q 4 determine the amplitude values of the vibrations of the system under consideration, the solution of the system of equations (2) and the determination of their absolute values requires solution.
b 1 = m kmS 2 + c km ; Ь 2 = - u km 1 ( bFS + C 1 ) ;
b’ = Ukm 0Fl + UkmbFR ; Ь4 = M1 Ukm 1S'i b5 = M 1 S2 + bFS + c1; b6 = M2S2;b7 = M3Ukm 1 S2;
b 8 = M 3 S 2; b 9 = M 4 S 2 + bSS + 2 c 2.
Expressions (3) allow the study of the dynamic character of the hysteresis type elastic dissipative characteristic plate and the liquid section dynamic absorber.
Let the external forces FL and FR acting between the opposite sides of the plate give the system acceleration W0 = e p * cos ® t ( e p * is the amplitude value of the base acceleration, e is a small parameter). In that case
FL = FR = - m km e P * cos ® t ■ (4)
The system of equations (3) is a complex expression. In order to determine their absolute values, we define the real and imaginary parts. To do this, we move from the variable S to the variable j ® . In this case, we take into account that the expression of modal stiffnesses сkm is a complex expression, ie
Ckm = C 1 km + jC 2 km , (5)
where с 1 km and с 2 km are the real and imaginary parts of the expression of modal stiffnesses сkm , respectively.
As a result, the absolute value of the first equation of the system of equations (3) is:
I I P« 2 + P2
q kma = e P * m km |Ukm *U D2 , „2 , V R 0 + R1
where
p0 = p 0 + p 1 ®+ p 2 ® 2 + p 3 ® 3 + p 4 ® 4;
P1 = P 5 + P 6 ® + P 7 ® 2 + P 8 ® ’ ;
R 0 = r0 + r 1 ® + r 2 ® 2 + r 3 ® 3 + r 4 ® 4 + r 5 ® 6 ;
R 1 = r 6 + r 7 m + r 8 m 2 + r 9 m 3 + r 10 m 4 + r nm 5;
p 0 = 2 с 1 с 2; p 1 = 0; p 2 = - ( с 1 M 4 + bFbS + 2 с 2* M 1 ) ; p 3 = 0;
p. = A = MM, - MM, ; p, = 0; p, = 2 bF с. + b с ; p = 0;
4142356 F 2 S 17
p 8 = -( bFM 4 + b S M 1 ) ;
r 0 = 2 с 1 с 2 с 1 km ; Г 1 = - ( 2 bF с 2 + bS с 1 ) с 2 km ;
r 2 = - ( с 1 M 4 + bF b S + 2 с 2 M 1 ) с 1 km - 2 с 2 с 1 ( m km + u km 1 M 1 ) ;
r 3 = ( bFM 4 + bSM 1 ) с 2 km ;
r4 = Aс1 km + mkm (M4c1 + bFbS + 2с2M1 ) + uL 1 ( C1A + bFbSM1 ) • r5 = -mkm A; r6 = 2с1 с2с2km ; r7 = ( 2bFс2 + bSс1 ) с1 km ;
r 8 = - ( с 1 M 4 + bFbS + 2 с 2 M 1 ) с 2 km ;
r 9 = - ( b F M 4 + b s M 1 ) с 1 km - ( 2 bF c 2 + bs c 1 ) ( mm + u km 1 M 1 ) ;
-
r 4* = A с 1 km + u km 1 ( M 1 bFbS + A с 1* ) +
-
+ ( 1 - u km u km * ) m km ( M 4 c 1 + bFbS + 2 с 2 M 1 ) ;
-
r 5* = -A m km ( 1 - u km u km * ) ;
-
r 9* =- ( bFM 4 + bSM 1 ) с 1 km -
-
- ( m m + u km 1 M 1 + u km m km u km * ) ( с 1 bS + 2 с 2 bF ) ;
r 11* = U L1 bF A + ( 1 - ukmukm * ) m km ( M 4 bF + bSM 1 ) •
We obtain mode shapes for transverse vibrations with the liquid section dynamic absorber mounted on the ab geometric center x1 = 2, y1 = 2 of the plate, the two opposite sides of which are fixed and the other two opposite sides are free:
к x , П kx , n my . „ . , n kx . , n my . u. x , y = B, cos h ---cos h —— + B , sin h ---sin h —— + km , 12 ab ab
П kx n my . _ . n kx . n my
+ B, cos---cos —— + B. sin---sin ——,
3ab4ab r10 A с 2 km ;
r 11 = m km ( bFM 4 + bSM 1 ) + u k m 1 bF A u km * = u km 0 + u kmb •
The expression (6) represents the amplitude-frequency characteristic of the system under consideration.
Absolute acceleration of the plate
where
B 1 = B 3
S p * D 8 p *
± т 2 , B2 = + T 2 , 2qkma m 2qkma m
B 4 =±
ее ее
Wkma = W > + w km ,
4 D n2 ( ( mb ) 2 + ( ka ) 2 )
8 p * [ \ ' ' ' /
2 q kma l m 2 km ( ab ) 3
where w km = u km ( x , У ) 4 km ( t ) •
Using the absolute acceleration expression, we obtain the ratio of the acceleration expression to the base acceleration expression as follows:
(sinh ( n k ) sinh ( n m ) - ( cosh ( n k ) - 1 ) x
x( cosh (nm)-1)) ±
±m 2
( ( 2 с 2 M 1 -m 2 A ) + ( M 1 bs m ) 2 ) ( c 12 + ( bF m ) 2 )
w = 1 -
W km 1
m 2 u, q, km q km
• •
W 0
x
The result obtained (8) is the transfer function of the system under consideration.
We put the first equation of the system of equations (3) into the transfer function (8). As a result, we get its absolute value.
I W km l = a G + G • (9)
V R 0 + R 1
where
G о = r 0 + h™ + r 2 * m 2 + r 3 m 3 + r 4 * m 4 + r 5 * m 6 ;
G 1 = Г + Г 7Ю + / '8(1)2 + / 9*0)3 + Г №Ю4 + Г ц.Щ5 ;
f , kk , nm . , nk . , nm Y x cosh—cosh--sinh—sinh— I,
I 2 2 2 2 JJ
4 D n 2 ( ( mb ) 2 + ( ka ) 2 ) km ( ab ) 3
±m 2
( ( 2 с 2 M 1 - m 2 A ) + ( M 1 bs m ) 2 ) ( c 12 + ( bF m ) 2
P0 + P 1
r 2* = - ( с M 4 + bF b s + 2 с 2 M 1 ) с km + + 2 с 1 с 2 ( m km + u km 1 M 1 - u km m km u km * ) ;
In order to perform numerical calculations on the obtained results, we take the aluminum alloy AL19 for the plate material:
л N _ „ N
E = 6 964119 - 10 4 —f , G = 26 487 - 10 6 ;
m 2 m 2
p = 2780 kg 3 ; ц n = 0,32.
m 3
Let the sides of the plate be a = b = 2.6 m , and the thickness h = 3 - 10 - 3 m . In that case the natural frequency of the plate for k = m = 1 will be © 11 = 13.4 s - 1.
Based on the results obtained in the study [33], we take the parameters of the liquid section dynamic absorber as follows:
bS = 264,7 - 10 3 - —; m v = 0,524 kg ;
m m2 = 1,456 kg; m3 = 3,665 kg; m 4 = 0,314 kg.
We select the remaining parameters as follows:
NNs m1 = 6.987 kg; c1 = c 2 = 106 —; bF = 106 —.
mm
Here are the experimental relationships between logarithmic decrement and normal, shear stresses [37]:
Table 1
The relationship between normal stresses and logarithmic decrement
|
a , k— / m 2 |
29430 |
39240 |
58860 |
78480 |
98100 |
|
f ( 6 . ) , % |
0.36 |
0.45 |
0.57 |
0.65 |
0.69 |
Table 2
The relationship between shear stresses and logarithmic decrement
|
t , k— / m2 |
9810 |
19620 |
29430 |
39240 |
49050 |
|
f ( ^ * ) , % |
0.1 |
0.1 |
0.28 |
0.63 |
1.04 |
Based on Tables 1 and 2, using the method presented in [38], we define the first three terms of the coefficients of logarithmic decrements [33].
-
5 = D q kma +^ + D n q kma ; (11)
-
5 = K 1 q kma +- + KC a • (12)
As a result, these coefficients are as follows:
D 1 = 10.6662475; D 2 =- 55.22539871 - 10 2 ;
D 3 = 10.434 6 6067 - 10 5 ;
K 1 = 6.570000005; K 2 =- 13.85 1 00 0 02 - 10 3 ;
K 3 = 91.85400011 - 10 5 .
We obtain the coefficients v,, v,,, n , n,, as v, =n. = —, 122 1 22 1 1 4
-
V 22 = ^ 22 = [33].
П
The real and imaginary parts of the expression of modal stiffnesses сkm can be calculated:
c m = 4198.222003 - 22146.23517 q 11 a -- 1721230.096 q 121 a - 705218.2446 q 131 a ;
c 211 = 9399.154126 q 11 a + 730512.7413 q 121 a + + 299303.9188 q 131 a .
Based on the above values of the parameters, we make a numerical analysis of obtained analytical expressions ( £ p * = 0.01 m ). First we draw graphs of functions (13) and (14).
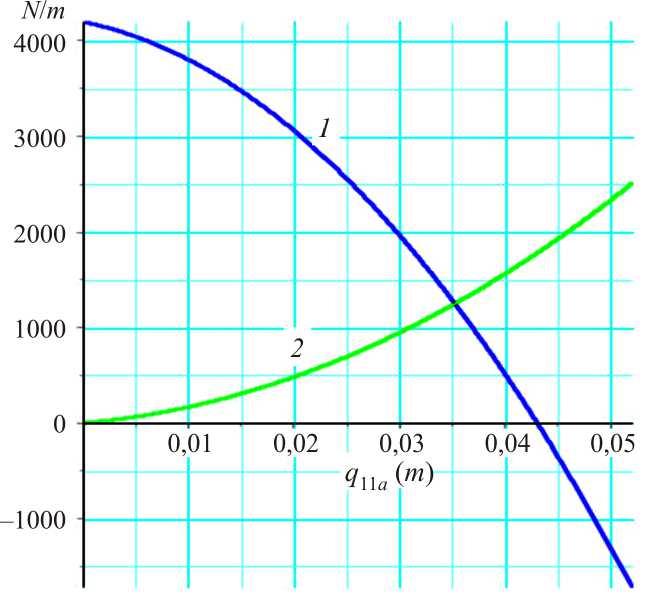
Fig. 2. Graphs of functions c 111 and c 211 (lines 1 and 2 , respectively)
As can be seen from Fig. 2, the c 111 function decreases with respect to the amplitude, while the c 211 function increases. Given that the c 1 km function represents the vertical deviation of the amplitude-frequency characteristic and the c 2 km function represents the energy dissipation in the plate material [33], it can be concluded that as the amplitudes increase, the vertical deviation of the system amplitude frequency characteristic decreases and the energy dissipation increases.
We draw the graph of the amplitude-frequency characteristic of the system under consideration.
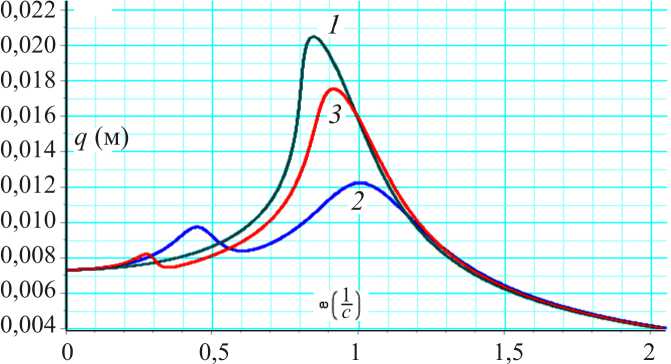
Fig. 3. The changing of the amplitude-frequency characteristic
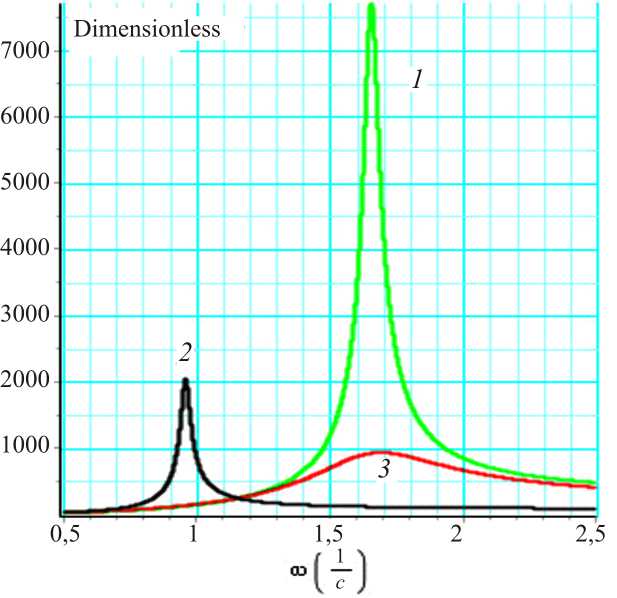
Fig. 4. The changing of the absolute value of the transfer function
Figure 3 shows the change in the frequency amplitude characteristic of the system under consideration depending on the elastic and damping elements of the liquid section
N , nN • s , dynamic absorber (c1 = 10—; bF = 10---- (dark green, mm line 1), c1 = 102 N; bF = 102 — (blue, line 2), c1 = 106 N; mm m
N • s bF = 106----- (red, line 3)). It can be said that the plate
m material has a soft characteristic from the vertical to the left shift of the graphs in the Fig. 3. It is also possible to see the effectiveness of the use of the liquid section dynamic absorber in the quenching of harmful vibrations of the plate at low frequencies.
In the field of values c1 < 104—; bF < 104 ^ s , the mm efficiency of the liquid section dynamic absorber is high, and the amplitudes reach the lowest values.
Draw the graph of the absolute value of the transfer function ( q 11 a = 0.009 m ).
Figure 4 shows the change in the absolute value of the transfer function depending on the elastic and damping elements of the liquid section dynamic absorber ( c 1 = 10 4— ; bF = 10 4 ^ s (green, line 1 ), c 1 = 0; bF = 0 mm
-
2 N , 2 N • s
(black, line 2), c1 = 102—; bF = 102----- (red, line 3)). It mm can be seen from these graphs that the transfer function
2 N 2 N • s reaches a small value when c1 = 10 —; bF = 10 ----.
mm
These values are the optimal values for the elastic and damping elements of liquid section dynamic absorber.
Conclusion
-
1. The amplitude-frequency characteristic and transfer function of the elastic dissipative characteristic of the hysteresis type plate vibrations, protected from vibrations under the influence of kinematic excitations, were expressed analytically depending on the system parameters.
-
2. A methodology for studying the dynamics of the plate protected from vibrations using amplitude-frequency characteristics and transfer function was developed.
-
3. It has been shown that the expression of the amplitude-frequency characteristic allows the selection of system parameters that achieve the minimum value of the displacement of the plate points protected from vibrations.
-
4. The effectiveness of the liquid section dynamic absorber in quenching low-frequency harmful vibrations of the plate has been demonstrated as a result of numerical calculations.
-
5. The resonance curves bend from vertical to the left, indicating that the plate material (when AL19 aluminum alloy is taken as the material) has a soft characteristic.
Список литературы Evaluation of the dynamics of elastic plate and liquid section dynamic absorber
- Birman V., Rusnak I. Vibrations of plates with superelastic shape memory alloy wires. J Eng Math., 2011, vol. 78 (1), pp. 223–237. DOI 10.1007/s10665-011-9483-3
- Zhili L., Xiliang Ch., Bo Zh., Zhili L., Xiliang Ch. Energy finite element analysis of vibrating thin plates at high frequency, IEEE International Conference on Cybernetics and Intelligent Systems and IEEE Conference on Robotics, Automation and Mechatronics, Ningbo, China, 2017, 17573973, DOI: 10.1109/ICCIS.2017.8274783
- Dal H., Morgül Ö.K. Vibrations of elastically restrained rectangular plates. Scientific Research and Essays, 2011, vol. 6 (34), pp. 6811–6816. DOI: 10.5897/SRE11.356
- Changjian J., Linquan Y., Jiping Sh., Tonghao H., Cheng L. In-plane free vibration of functionally graded rectangular plates with elastic restraint. Global Journal of Engineering Sciences. 2019, vol. 2 (3), pp. 1–8. DOI: 10.33552/GJES.2019.02.000537
- Zhong Y., Zhao X., Liu H. Vibration of plate on foundation with four edges free by finite cosine integral transform method. Latin American Journal of Solids and Structures, 2014, vol. 11, pp. 854–863. DOI: 10.1590/S1679-78252014000500008
- Stojanović V., Kozić P., Ristić M. Vibrations and stability analysis of multiple rectangular plates coupled with elastic layers based on different plate theories. International Journal of Mechanical Sciences, 2015, vol. 92, pp. 233–244. DOI: 10.1016/J.IJMECSCI.2014.10.027
- Xiao-Dong Yang, Li-Qun Chen, Jean W. Zu. Vibrations and stability of an axially moving rectangular composite plate. Journal of Applied Mechanics, 2011, vol. 78 (1), pp. 1–11. DOI: 10.1115/1.4002002
- Kurpa L., Mazur O., Tkachenko V. Dynamical stability and parametrical vibrations of the laminated plates with complex shape. Latin American Journal of Solids and Structures, 2013, vol. 10 (1), pp. 175–188. DOI: 10.1590/S1679-78252013000100017
- Wang Y., Wu H., Yang F., Wang Q. An efficient method for vibration and stability analysis of rectangular plates axially moving in fluid. Applied Mathematics and Mechanics, 2021, vol. 42, pp. 291–308. DOI: 10.1007/s10483-021-2701-5
- Zhang D., Tang Y., Chen L. Internal resonance in parametric vibrations of axially accelerating viscoelastic plates. European Journal of Mechanics – A/Solids, 2019, vol. 75, pp. 142–155. DOI: 10.1016/J.EUROMECHSOL.2019.01.02
- Stian S., Eilif P. The theory of bond graphs in distributed systems and simulations, Proceedings of the International Conference on Bond Graph Modeling and Simulation, Montreal Quebec Canada, 2016, pp. 147–156.
- Cezary O., Rafał H. Modelling and analysis of beam/bar structure by application of bond graphs. Journal of theoretical and applied mechanics, 2011, vol. 49 (4), pp. 1003–1017.
- Migdalovici M., Baran D. Theoretical research regarding any stability theorems with applications, Proceedings of the 14th international congress on sound and vibration, Cairns, Australia, 2007, pp. 575–581.
- Vinayak R., Ghosh M.K. Forced vibration response of thin plate with attached discrete dynamic absorbers. Thin-Walled Structures, 2005, vol. 43, pp. 1513–1533.
- Mohammad A.G., Amr M.O. Vibrations analysis of rectangular plates with clamped corners. Open Engineering, 2018, vol. 8, pp. 275–283. DOI: 10.1515/eng-2018-0030
- Patrick D., Dominic M., Fadi A., James A., Inès Ch. Simplified setup for the vibration study of plates with simply-supported boundary conditions. MethodsX, 2019, vol. 6, pp. 2106–2117.
- Ramu I., Mohanty S.C. Study on free vibration analysis of rectangular plate structures using finite element method. Procedia Engineering, 2012, vol. 38, pp. 2758–2766.
- Torabi K., Azadi A.R. Vibration analysis for rectangular plate having a circular central hole with point support by Rayleigh- Ritz method. Journal of Solid Mechanics, 2014, vol. 6 (1), pp. 28–42.
- Mohamed F.Y. Effect of different design parameters on damping capacity of liquid column vibration absorber. Journal of Engineering and Applied Science, 2018, vol. 65 (6), pp. 447–467.
- Linsheng H., Wenhe Sh., Hongnan L., Yaowen Zh. Optimal design of liquid dampers for structural vibration control based on GA and H norm. Smart Control Algorithms and Technology in Civil Infrastructures, 2013, vol. 2013, ID 191279, DOI: 10.1155/2013/191279
- Tanveer M., Usman M., Khan I.U., Ahmad S., Hanif A., Farooq S.H. Application of tuned liquid column ball damper for improved vibration control performance of multi-storey structure. PLoS ONE, vol. 14 (10), ID e0224436, DOI: 10.1371/journal.pone.0224436
- Jans V., Līga G. Overview of tuned liquid dampers and possible ways of oscillation damping properties improvement, Proceedings of the 10th International Scientific and Practical Conference. Rezekne, Latvia, 2015, pp. 233–238. DOI: 10.17770/etr2015vol1.230
- Alberto Di M., Mario Di P., Antonina P. Innovative modeling of tuned liquid column damper controlled structures. Smart Structures and Systems, 2016, vol. 18 (1), pp. 117–138. DOI: 10.12989/sss.2016.18.1.117
- Swaroop K.Y., Ahsan K., Jeffrey C.K. Semi-active tuned liquid column dampers for vibration control of structures. Engineering Structures, 2001, vol. 23, pp. 1469–1479.
- Swaroop K.Y., Ahsan K. Semiactive tuned liquid column dampers: experimental study. Journal of structural engineering, 2003, vol. 129 (7), pp. 960–971.
- Espinozaa G., Carrilloa C., Suazoa A. Analysis of a tuned liquid column damper in non-linear structures subjected to seismic excitations. Latin American Journal of Solids and Structures, 2018, vol. 15 (7), pp. 1–19. DOI: 10.1590/1679-78254845
- Hamidreza F., Mehdi Sh., Roozbeh P. Application of tuned liquid column damper for motion reduction of semisubmersible platforms. International journal of coastal & offshore engineering, 2020, vol. 4 (2), pp. 23–40.
- Xiaohui Z., Yang Y., Liang Zh., Qingquan L., Han W. A new energy-absorbing device for motion suppression in deepsea floating platforms. Energies, 2015, vol. 8, pp. 111–132. DOI: 10.3390/en8010111
- Alberto Di M., ·Thomas F., ·Christoph A., ·Antonina P. Optimal design of tuned liquid column dampers for seismic response control of base-isolated structures. Acta Mech, 2018, vol. 229, pp. 437–454. DOI: 10.1007/s00707-017-1980-7
- Ahmedov O., Mirsaidov M. Finite element of rotating wheelset and its natural frequencies determination. Materials Physics and Mechanics, 2021, vol. 47 (5), pp. 706–719
- Mirsaidov M.M., Khudainazarov Sh.O. Spatial natural vibrations of viscoelastic axisymmetric structures. Magazine of Civil Engineering, 2020, vol. 96, pp. 118–128. DOI: 10.18720/MCE.96.10
- Mirsaidov M.M., Mamasoliev Q. Contact problems of multilayer slabs interaction on an elastic foundation. IOP Conference Series Earth and Environmental Science, 2020, vol. 614 (1), ID 012089, DOI: 10.1088/1755-1315/614/1/012089
- Pavlovsky M.A., Ryzhkov L.M., et al. Nelinejnye zadachi dinamiki vibrozashhitnyh sistem [Nonlinear problems of the dynamics of vibration protection systems]. Kiev, Technique, 1997, 204 p.
- Mirsaidov M.M., Dusmatov О.М., Khodjabekov М.U. Stability of nonlinear vibrations of plate protected from vibrations. Journal of Physics: Conference Series, 2021, vol. 1921, ID 012097, DOI: 10.1088/1742-6596/1921/1/012097
- Mirsaidov M.M., Dusmatov О.М., Khodjabekov М.U. The problem of mathematical modeling of a vibration protected rod under kinematic excitations. IOP Conference Series Materials Science and Engineering, 2021, vol, 1030 (1), ID 012069, DOI: 10.1088/1757-899X/1030/1/012069
- Mirsaidov, M., Dusmatov, O., Khodjabekov, M. Mode shapes of transverse vibrations of rod protected from vibrations in kinematic excitations. Lecture Notes in Civil Engineering, 2022, vol. 170, pp.217–227. DOI.org/10.1007/978-3-030-79983-0_20
- Pisarenko G.S., Yakovlev A.P., et al. Vibropogloshhajushhie svojstva konstrukcionnyh materialov [Vibration-damping properties of construction materials]. Kiev, Dumka, 1971, 327 p.
- Pisarenko G.S., Boginich O.E. Kolebanija kinematicheski vozbuzhdaemyh mehanicheskih sistem s uchetom dissipacii jenergii [Vibrations of kinematically excited mechanical systems taking into account energy dissipation]. Kiev, Dumka, 1981, 219 p.


