Evolutionary Image Enhancement Using Multi-Objective Genetic Algorithm

Published Online November 2013 in MECS

Genetic Algorithm stands for a class of stochastic optimization methods that simulate the process of natural evolution. Multi-Objective Genetic Algorithm has been proposed to solve multi-objective optimization problems, accompanied with masses of multi-objective applications. Multi-Objective Genetic Algorithm has ability to exploit and explore solutions in parallel and to find a wide spread set of non-dominated solutions in a single run. A Multi-Objective Optimization Problems (MOOPs) differs from a Single-Objective Optimization Problems (SOOPs). it contains several objectives that requires optimization for a single objective problem, the goal is best single design solution. But with MultiObjective Optimization Problem with several objectives, there is usually no single optimum solution, so decision makers are required to select a solution from a finite set by making compromises or a complete set of pareto-optimal solutions. These solutions are optimal in the wider sense that no other solutions in the search space are superior to them when all the multiple objectives are consideration. Multi-Objective Optimization is sometimes referred as vector optimization, because a vector of objectives, instead of a single objective, is optimized. Multi-Objective Optimization Problems can be of many types:

• (a)      Linear MOOP

• (b)     NonLinear MOOP

• (c)     Convex MOOP

• (d)     NonConvex MOOP

If all the objective functions areli near, the resulting MOOP is called a Multi-Objective Linear Program (MOLP). For a NonLinear MOOP, if all the objective functions are non linear, the resulting MOOP is called a Non Linear Multi-Objective Problem. For Non Linear problems, the solution techniques often donot have convergence proof. And for a Convex MOOP, if all the objective functions are convex and the feasible region is convex.

There are two approaches for solving Multi-Objective Optimization Algorithm; they are Ideal Approach and Preference Based Approach. In Ideal approach, no special importance is given to any particular objective and a set of trade off or Pareto Optimal solutions are desired to be found. After a set of Pareto Optimal solutions (or near to Pareto Optimal solution) is found, some higher-level information is needed regarding the problem for choosing one solution from the obtained set of solutions. Evolutionary Multi-Objective Optimization Algorithm follows this approach. In Ideal approach of Multi-Objective Optimization, two tasks must do well, they are –

• (i)    Converge as close to the true Pareto Optimal solutions as possible.

• (ii)     Maintain as diverse a population as

possible classification.

In most of Multi-Objective Evolutionary Algorthms (MOEAs), convergence towards the Pareto Optimal front is achieved by assigning a fitness based on the non domination ranking of solution. Diversity among solutions is achieved by using an explicit niching or crowding operation.

In Preference Based Approach, Instead of finding a set of Pareto Optimal solutions, the focus is to find one of the Pareto Optimal solution based on a user-specified relative importance vector for the objectives.

Classical Multi-Objective Optimization Algorithms follows this approach. In Classical Multi-Objective Optimization there exist no studies related to nondominated sorting.

Various research has been done in the area of image enhencement using Multiobjective Genetic Algorithm. The First Multi-objective Genetic Algorithm was Vector Evaluated Genetic Algorithm (VEGA) which was proposed by Schaffer [1]. VEGA is based on population based approach means; it is able to produce multiple non-dominated solutions concurrently in a single simulation run. VEGA has many problems because its selection mechanism is opposed to the concept of Pareto dominance means that, Pareto dominance is not directly embedded in the selection process. This algorithm is only suitable in which the selection mechanism is biased. Afterward, Multi Objective Genetic Algorithm proposed by Fonesca and Fleming [2] came in to existence in which each individual in the population is ranked based on how many other points dominate them. Then after Niched Pareto Genetic Algorithm (NPGA) proposed by D. E. Goldberg [3] in which an interesting form of tournament selection called Pareto domination tournaments are used. In this scheme, two members of the population are chosen randomly and they are each compared to a subset of the population. If one is nondominated and the other is not, then the non-dominated one is selected. If there is a tie (means both are either dominated or non-dominated), then fitness sharing decides the tournament results. Afterwards Random Weighted Genetic Algorithm [4] was proposed which produces better results. N. Srinivas and K. Deb developed Non-dominated Sorting Genetic Algorithm (NSGA) [5] and implements a new stochastic remainder proportionate selection mechanism for fitness assignment in the algorithm. To preserve the diversity in the population, a new algorithm called Strength Pareto Evolutionary Algorithm (SPEA) [6] is best but it is not capable to preserve the boundary solutions. Another Multi-Objective Genetic Algorithm called Pareto Archieved Evolutionary Strategy (PAES) [7], which was developed by J. D. Knowles and D. W. Corne having the disadvantage in terms of performance on disconnected pareto fronts. In the field of image enhancement using multiobjective criteria, there is no general method at present because it depends on the quality of the image. Some particular methods has been explained in this field for a particular type of image by [8][9][10]. R. Poli [11] used some pseudo-coloring algorithm, J.S. DaPonte [12] used gradient operators, G. Ramaponi [13] used unsharp masking methods, Yang [14] used optimal feature extraction of ‘edge of the image’, K. Li [15] used a set of proper filter for image enhancement. C. Munteanu [16] proposed image enhancement criteria using eolutionary algorithms on the basis of three objectives namely entropy, number of edges and intensity. This paper proposes a method to enhance the gray scale image by sharpening the features or maximizing the three objectives namely intensity, no. of edgles and entropy with the help of Evolutionary Genetic Algorithm by incorporating multi objective criteria in order to find the best image. Since in any image, number of edgels, intensity and contrast plays an important role to explore most of the descriptions about the image. Therefore, we have taken multi objectives criteria and, Genetic Algorithm because the ability of an Genetic Algorithms is to find multiple optimal solutions in one single simulation run makes it's uniqueness. Also Genetic Algorithms uses a population of solutions in each iteration and other methods mostly uses only one solution that’s why Genetic Algorithms known as a population based approach and other methods known as a Point to Point based approach.

The present paper is organized in four sections. First section namely; Introduction, describes the introduction and previous research on genetic algorithm and image enhancement methods, second section describes proposed algorithm, third section describes experimental results. In this section we have compare our proposed method with other enhancement methods: Histogram equalization [9], 2D Median filtering method [19] and BPDF Histogram equalization method [20]. Last section describes conclusion of this paper and future prospects.

• II.    PROPOSED ALGORITHM DESCRIPTION : IMAGE

E NHANCEMENT M ETHOD B ASED O N E VOLUTIONARY A LGORITHM

Evolutionary Algorithms (EAs) are methods that take their inspiration from natural selection and survival of the fittest in the biological world. EAs are different from traditional optimization techniques in the way that they involve a search from a ‘population’ of solutions, not from a single point. Each iteration of an EA involves a competitive selection that weeds out poor solutions. The solutions with high ‘fitness’ value are recombined with other solutions by swapping parts of a solution with another. Solutions are also ‘mutated’ by making a small change to a single element of the solution.

The goal of image enhancement is to accentuate certain image features for subsequent image analysis, for example edge enhancement, change in contrast, noise filtering, sharpening and magnifying etc. Image enhancement is very useful in feature extraction, image analysis, visual information display and so on. We propose an enhancement method, which is similar to the local transformation based method proposed by Munteanu and Roas [16] is given as:

g ( x , y ) = k * { M/( a ( x , y ) + b } * { f ( x , y ) - c * m ( x , y ) } + m ( x , y ) a ⁽¹⁾

where,

g(x, y) stands for output pixel intensities,

f(x, y) stands for input pixel intensities,

M stands the global mean,

σ(x,y) and m(x, y) stands for the local standard deviation and mean calculated in the neighborhood of 3x3, a,b,c and k are tunable parameters.

3x3 neighbourhood around a point (x,y) in an image is shown below-

Chromosomes of image are represented as an array of real integer of length four [a, k, b, c] where a, k, b and c are the enhancement parameter, ranging from 0 to1.5, 0.5 to 1, 0 to 0.5 and 0 to 1.0 respectively. We proposed some changes in the value of the parameters a, k, b and c while in [16] to produce the better results. We proposed the enhancement criteria, by considering the hypothesis that a best image can have :

• (i)      high number of edges,

• (ii)      high intensity value,

• (iii)     high entropy value.

The number of edgels and itensity values are calculated with the help of ‘Sobel derivative’ method. Edges in an image can be defined as a rapid changes in image intensity over a small region. We are using Sobel operator to detect edges. Sobel operator consist of two masks which calculate the changes in both the direction i.e. in x-direction and y-direction both.

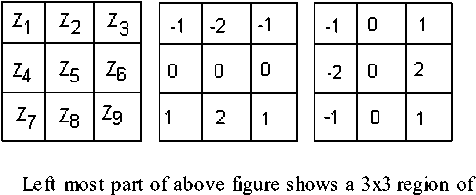
an image, Z’s are gray level values and masks are used to compute gradient at point Z5 . In middle part of the figure, Sobel mask for gradient component Gx and right most part of figure, Sobel mask for gradient component Gy has geen shown.

For image pixel I(x,y), labeled as Z₅ , as above-

Gy = ( Z 3 +2*Z 6 +Z 9 ) - ( Z 1 +2*Z₄+Z 7 )

and Gradient = [Gx ² + Gy ² ]^1/2

Now number of edgels are calculated by calculating gradients at every pixel in the image.

We have proposed a fitness function criteria which is based on individual objectives. After evaluating fitness of all individual objectives (Entropy, Edge and Intensity), combined fitness or cumulative fitness is calculated which is totally different from the way that fitness function is calculated by C. Munteanu [16] on the basis of all the objectives at a time.

We applied Tournament selection which operates by choosing some individuals randomly from a population and selecting the best from this group to survive in the next generation. The Crossover means Exchange of genetic material to form children. Once Selection has chosen fit individuals, they must be randomly altered with hope of improving their fitness for the next generation. In Crossover, two individuals are chosen to swap segments of their code, to produce offsprings. We have used Arithmetic Crossover [17]. In Arithmetic Crossover, some arithmetic operation is performed to make a new offspring and it can be defined as a linear combination of two chromosomes such as :

c1=a*x+(1-a)*y                                (2)

c2=(1-a)*x+a*y                                 (3)

Where c1 and c2 are offspring or child1 and child 2 respectively. x and y be two parents in the mating pool and a is a random number where a Є [0,1].

Algorithm Steps:

Step 1: Create an initial population

Step 2: Calculate the objective functions for the current population

Step 3: Apply cumulative fitness assignment criteria and selection procedure

Step 4: Apply the NSGA II [8] Algorithm for selection of new population.

Step 5: Find Pareto Optimal front (POF).

Step 6: Select the best individuals from the POF. For best individuals, find the number of individuals dominated by that individual, then select one of them having maximum number of dominated individuals.

Step 7: Apply Crossover and Mutation on the new population (obtained at Step 4) for creating a new population.

Step 8: Display Image using best individuals (obtained at Step 6).

Step 9: Apply local enhancement.

Step 10: Show the enhanced image.

Gx= ( Z 7 +2*Z 8 +Z 9 ) -Z 1 +2*Z₂+Z₃ )

• III.    EXPERIMENTAL RESULTS

We proposed an enhancement technique using multiobjective criteria via real coded genetic algorithm i.e. ‘IEEALGO (Intensity Edge and Entropy) algorithm’ and compared with Histogram equalization [9], C. Munteanu [16], Sobel method [18], 2D Median filtering [19] and BPDF Histogram equalization [20]. Visually, in Fig. 1-4; we have shown enhancement results using various methods. We have used 4 numbers of images and experimentally found that applying Genetic Algorithm in between 40 to 50 generations gives better results. We have choosen chrosome of length 4 with population size 48 and arithmetic crossover alongwith simple mutation is used.

In our experimental results, we have used various tables (Table I to Table V) and figures (Figure 1 to Figure 4). Table I shows size of experimental images and number of generations to run the Genetic Algorithm for those images; Table II displays the fitness values given by C. Munteanu [16] and our proposed method. In Table III we compared the number of edgels calculated with the help of Sobel Edge detector method, Histogram equalization, 2D Median filtering method, BPDF Histogram equalization and the edges generated by the proposed method. In Table IV we have shown the comparision of entropy value of different methods, and in Table V, we have shown and compare the third objective intensity.

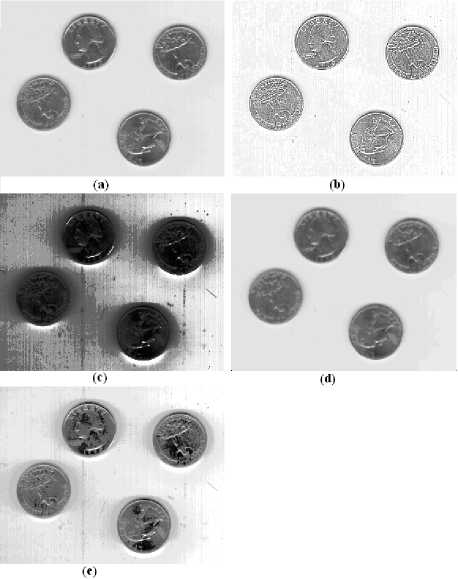
Figure 2. ‘eight’; Enhancement results (a) original image; (b) proposed method; (c) Method[9] (d) Method[19] (e) Method[20]

Figure 3. ‘pout’; Enhancement results (a) original image; (b) proposed method; (c) Method [9] (d) Method [19] (e) Method [20]

«■>

Figure 1. ‘cameraman’; Enhancement results (a) original image;(b) proposed method; (c) Method [9] (d) Method [19] (e)

Method [20]

(е)

Figure 4. ‘Tire’ ; Enhancement results (a) original image; (b) proposed method; (c) M ethod [9] (d) Method [19] (e)Method [20]

Now we are showing the mathematical results which are calculated by our proposed method and other methods with the help of tables.

TABLE I. IMAGE SIZE AND MAXIMUM NUMBER OF GENERATIONS USED IN THE PROPOSED METHOD

Sl. No.	Image Name	Size (in pixels)	Generations
1	Cameraman	256 X 256	40
2	Eight	242 X 308	50
3	Tire	205 X 232	40
4	Pout	291 X 240	50

In Table II, we have compared fitness value for different images with the method given by Munteanu and Roas [16] and the proposed method. As it is clear from the table that proposed method scores high values.

TABLE II. RESULTS OF FITNESS VALUE OF THE IMAGES

Sl. No.	Image Name	Munteanu & Rosa [16] Method	The proposed method
1	Cameraman	100.975	2666
2	Eight	159.947	2680
3	Tire	2.394	2703
4	Pout	124.001	2671

Table III shows a comparision of number of edgels calculated using our proposed method and other existing methods : Sobel edge detector method[18], Histogram equlization method[9], 2D Mean filterinmg method[19], BPDF Histogram equalization method[20]. It is interesting to note that, ‘pout’ image has less number of edgels, but for others, our proposed method scores higher values. Thus, overall, the proposed method shows better performances.

Table III. NUMBER OF EDGELS IN IMAGES

Sl. No	Image Name	Method [18]	Method [9]	Method [19]	Method [20]	The proposed method
1	Cameraman	2485	2405	2063	2497	2864
2	Eight	2658	1439	1726	2950	3656
3	Tire	1823	1963	1660	1653	1884
4	Pout	1492	1947	1463	2936	1904

In Table IV, Entropy values for different enhanced images by using the proposed method and other methods are given.

TABLE IV. ENTROPY VALUES OF IMAGES USING DIFFERENT METHODS

Sl. No	Image Name	Original	Method [9]	Method [19]	Method [20]	I The proposed method
1	Cameraman	7.009	5.910	6.948	6.712	7.42
2	Eight	4.879	4.184	4.791	4.723	5.577
3	Tire	6.926	5.614	6.899	6.549	5.985
4	Pout	5.759	5.459	5.715	5.595	7.173

In Table V, we have given intensity values of the original images as well as enhance images by different methods. Here intensity values are generated by our proposed method and other methods : Histogram equlization method[9], 2D Mean filterinmg method[19], BPDF Histogram equalization method[20]. The value of the Intensity which are calculated by our proposed method shows high.It is clear from the table that our proposed method perform best for all the images.

TABLE V. INTENSITY VALUES OF IMAGES (IN TERMS OF STRINGS)

Sl. No	Image Name	Original	Method [9]	Method [19]	Method [20]	The proposed method
1	Cameraman	2507.304	3346.8	1952.1	2830	4035.64
2	Eight	1767.642	3083.4	1396.9	2497.2	3922.098
3	Tire	1862.428	2679.7	1627.3	1774.9	3994.24
4	Pout	1076.217	3052	945.365	1836.4	3020.464

Here, we are showing the histogram of enhanced images i.e. cameraman, eight, tire and pout, using the proposed method.

• IV.    C ONCLUSION

  

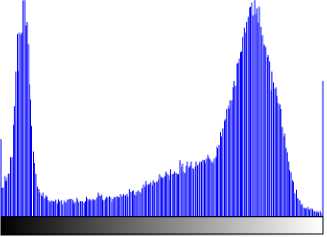
  Figure 5. histogram of enhanced image ‘cameraman’ using the proposed method

  
  

Image enhancement is intended to convert images in to a form that makes the use of capabilities of human visual system to perceive information to their highest degree. Therefore, to retrieve the maximum information about images, Image Processing techniques are used. Image enhancement procedures also utilize the computers to provide good and improved images for study by the human interpreters.

Figure 6 . histogram of enhanced image ‘eight’ using the proposed method

Figure 7. histogram of enhanced image ‘tire’ using the proposed method

As for future work we will concentrate on improving or extending our method in order to achieve better results by some modifications like mutation technique, fitness evaluation criteria, population size.