Exact relations between effective thermoporoelastic characteristics of porous composites

One of the important problem of the mechanics of heterogeneous materials is the so-called homogenization problem whereby a heterogeneous material is replaced by a homogeneous one having the same response to the external loading; see the review article [9] and books [7], [10], [13]. An interesting aspect of the problem is that certain effective characteristics of the homogenized material may be interconnected (cross-property relations). The simplest cross-property relations are due to mathematical analogy between the equations that govern different phenomena: dielectric and magnetic permittivity, electric and thermal conductivity etc. In such cases, results for one of the properties imply similar results for the other one in a straightforward way. In some cases, however the cross-property relations are much less trivial. An example is provided by heat transfer in a fiber reinforced medium in direction normal to the fibers and shear deformation along the fibers (see Hashin [5], Chap. 5.5.1). A more complicated example was given by Hill [6] who derived expressions for the transversely isotropic elastic moduli of a composite material reinforced by parallel fibers. Hill [6] showed that only three of the five elastic constants are independent for such a material. Similar relations have been obtained by Schulgasser [15] for the effective elastic, piezoelectric and dielectric characteristics of transversely isotropic piezoelectric composites with continuous reinforcement.

There is another grope of relations in which the characteristics of different properties are interconnected. The relations between the effective thermal expansion coefficients and effective elastic moduli of two-phase isotropic composites were established by Levin [8] (see also Schapery, [14]) and generalized by Rosen and Hashin [12] to the case of anisotropic materials. Relations between the thermal expansion and piroelectric coefficients and electroelastic moduli of thermoelectroelastic composites were obtained by Dunn [4]. Here we suggest a simple way to obtain cross-property relations for two-phase ther-moporoelastic composites. The poroelastic theory developed in the middle of the last century by Biot

[2], [3] found a wide application in geomechanics for modeling of the static and dynamic behavior of real porous rocks filled with fluids. Such geological material are often highly inhomogeneous, containing the regions with different poroelastic properties (different fluids, for example, different porosity and skeleton rigidity). Thus, the obtained in this paper cross-property relations may be usefull for the solution of the homogenization problem for inhomogeneous (composite) poroelastic materials.

The linear constitutive relations for an arbitrary anisotropic poroelastic medium with incorporated thermal effects can be written in the form

^j = Cijki£fci - ajP - nT, z = j + PP - YT,           (1.1)

5 = ПК - YP + cT, where εij and σij are the strain and stresses, p is the pore pressure, T is the temperature change from some reference temperature, Cijkl is the tensor of the frame (solid skeleton) elastic moduli, αij is the tensor of the effective stress coefficients, ηij is the tensor of the thermal stress coefficients, ζ is the pore strain, s is the entropy, c is the specific heat at the constant strain, β and γ are the Biot coefficients of thermoporoelastic coupling.

EFFECTIVE THERMOPOROELASTIC PROPERTIES OF TWO-PHASE COMPOSITES

We consider now a composite poroelastic material consisting of two homogeneous generally anisotropic components (phases) occupying the regions V , V , in some representative volume element V (V = V + V ₂). Suppose that the temperature T and pore pressure p are constant in V. The constitutive relations for such a material can be written in the form

^ ij ⁽ x ) = C ijki ⁽ x Ki ⁽ x ) ^{- a} j ⁽ x ) P ^- n j ⁽ x^)T , Z ( x ) = a j ( x K j ( x ) + в ( x ) P — Y ( x ) T ,         ^(2.1)

5 ( x ) = n j ( x ) £ y ( x ) - Y ( x ) P + c ( x )T ,

Exact relations between effective thermoporoelastic characteristics of porous composites

where is a point in 3D-space, Cijki ^{( x} ), О,- ^{( x} ), ⁿij ^{( x} ), ^e(x ), ^Y(^x ) and c ( x ) are random functions of coordinates taking the constant values ^, аЦ\..., c^m when x e V and C^, а^\ ..., c^<2) when x e V ₂ .

Let us introduce the characteristic function of the first phase V ( x )

( V ( x ) = 1 when x e V , V ( x ) = 0 when x t V ). Then, the functions C ijkl ^{( x} ), ^a j ^{( x} ), П , ⁽ x ) can be writ-

ten as	C ytt ( x ) = C iyti +A C yti V K x ), a ij ( x ) = a J 2) +A a y V ( x ), n iy ( x ) = n iy 2) + A n y V ( x ),	(2.2)
where	(l) _ л,(2) ijkl = ijkl       ijkl Aa y = a iy ) - a ij2) An ij = n J '’ - n iy 2)	(2.3)

We denote the averaging operation over the volume V as ⋅ . After averaging Eqs. (2.1) and accounting (2.2), we obtain

(^(x)) = Cit s (x)) + fACyH ^ B (x)) 1 - (a,(x^ p - (n,(x)} T, zz(x)) = ati2) (sti(x)}+fl Aati ^(x Д + e(x)) p - (y (x)} T,     (2.4)

(^c ) = n t 1 ²⁾ ( ^s ti ^{( x} )) ^{+ f} M_H fa ^{( x} )\ ^{+ Y ( x} )) p ^- c^{( ( x}»T .

Here (■ \ denotes the averaging over the region V , f is the volume concentration of the first phase.

Due to linearity of the problem tensor \sy(x)л has to be linear function of the average (sj(x)), pore pressure p and temperature T s s(x )\ = Qyki (s,(x))+qjp+KT,    (2.5)

where Q ijti , q , and ^K y are unknown quantities that are to be determined in some homogenization process.

Substituting relation (2.5) into (2.4) we have

(^ij ^{( x} )) = C ji ^h ^{( x} )) ^- j ^- n * ^T ,

(^{z (} x )) = a * i ^ ⁽ x ))+ ^e p - y* T ,        (2.6)

(^(x)) = nti ^ H (x)) - Y*p + c*T, where C*jkl, ai, nJ, в, У and c are the effective thermoporoelastic characteristics of composite material (the quantities that connect the averaged over V fields, pore pressure and temperature). These characteristics are defined by the relations

C j ti = C i ( x )} + f l A C m ( Q mnti - I _mnU ) , (2.7)

^a ij = ^a j ^{( x} )) ⁺ f l ^Aa ti ( QM u ^- IM j ) = j^x )) - f l ^{A C}._Jkl q kl , (2.8)

n * = ⁿ j ( x )} ⁺ f l ^An ti ( Q tij ^- I ki_IJ) = ⁿ j ( x )) - f l ^A С _уик_и , (2.9)

^e* = ( ^{e (} x ))⁺ f l ^{A a} j q ,j ,            (2.10)

Y* = ( Y ^{( x} ))- f l ^Aa j ^K ij = ( y ⁽ x ))- f l^A n ,j q j , (2.11) ^c * = ( ^{c ( x} ))⁺ f l ^An ij ^K ij ,              (2.12)

where ^I ijkl = ^A i( Д ) j and parenthesis denote symmetrization.

THE CROSS-PROPERTY RELATIONS FOR

TWO-PHASE THERMOPOROELASTIC COMPOSITES

Equations (2.7) imply that f (Qijti -Ijui) = (ACm)-1 (cmnti -C^nti^(x))). (3.1)

Now it follows from Eqs. (2.8), (2.9)

aij = (a,j (x)) + Aakl (ACtimn г1 (Cmnij - C^rnny (x))) , nij = (nij (x)) + Anti (ACtimn )-1 (Cmnij — (Cmn,j (x)}) - (3.3)

Because of flqj = -(ACJmn । ' (amn — (Omn (x))) , flKj =-(ACm । ' (nmn - (nmn(x))), we obtain from Eqs. (2.10) – (2.12)

^в‘ = ^{в ( x} )) ^-Aa ij ^{( A} C m г¹ ( ^a mn ^- ( ^a mn ^{( x} ))), (3.6)

У = ^{Y ( x} )) ^{+ Aa} ij ^{( A} C m ) - ( n mn ^- ( n mn ^{( x} )) ) =

= Y(x)> + An,j (ACijmn )- (a*mn - (amn (x))) , c‘ = (c(x)) + Anj(ACijmn г1 (nmn - ^mn (x))) - (3.8)

It follows that the tensor of the effective stress coefficients α ij , tensor of thermal stress coefficients ⁿ j , the Biot coefficients of thermoporoelastic coupling в , Y * and specific heat c * are not the independent characteristics, but are expressed in terms of those of two phases, the frame elastic moduli of two phases and effective elastic moduli of composite material. Equations (3.2), (3.3) and (3.6)–(3.8) are the exact results independent on the microstructure of the inhomogeneous poroelastic medium.

Hence, in any homogenization process for such a material it is necessary to find only the effective frame elastic moduli C yti . Then, the other effective constants of thermoporoelastic composite material can be calculated by the formulas (3.2)–(3.8).

Suppose that the both components of the inhomogeneous poroelastic medium are isotropic with bulk frame moduli Kl, K2, effective stress coefficients al, a2, thermal stress coefficients nl, n2. If the composite is also macroscopically isotropic with the effective bulk modulus Kj , then the formulas (3.2), (3.3) and (3.6)–(3.8) are transformed to ai = a8y, a = (a(x)) + 1 1 (К* - (K(x))), (3.9)

K 1 K 2

n * = nA , n* = ( n ⁽ x )) + ^{n n} ( к* -( K ⁽ x )) ) , (3.10) K 1 K 2

в=^xx^ - i-K (a * - a( x^)= r J у                  (3.11)

= e^ x »Aa-r I ( к * - K ( x )> ) , V K 1 K 2 )

У = (/to) = -^^(^ -('/to))

(а, -а.ХПх "ПЗ to-^2)²

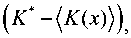
(3.12)

c * = cc ⁽ x )} ^- П - K ( n ^- ( n ^{( x} ))) =

,   1 V                   (3.13)

= < c ( x »-I .    .' I ( K • -( K ( x ») .

V K 1 K 2 )

These relations coincide with those obtained in [1], [11] by some other way.

CONCLUSIONS

The exact relations between the effective thermo-poroelastic characteristics (cross-property relations) of two-phase poroelastic composites were obtained and analyzed. These relations may be used in any homogenization procedure that establish the connections between the mathematical expectations of the field variables, pore pressure and temperature in the inhomogeneous poroelastic composite material.

Levin V. M., Mexican Oil Institute (Mexico City, Mexico)

EXACT RELATIONS BETWEEN EFFECTIVE

THERMOPOROELASTIC CHARACTERISTICS OF POROUS COMPOSITES