Excitation processes in Ar-Ar collisions

The importance of investigating non-elastic collisions of argon atoms is conditioned by their significant role in different scientific and technical applications. The determining of quantitative scattering characteristics in the conditions of a beam experiment plays a considerable role among the numerous research aspects of non-elastic collision of neutral particles. The low collision energy range is of special interest since theoretical treatment of non-elas-tic processes at such energies is rather complicated and, therefore, the quantitative data as well as the information on mechanisms of population of atomic levels can be obtained mainly in an experiment (see, for example, [7], [8], [10], [14], [15], [16]). The development of plasma physics, plasma chemistry, and astrophysics requires clarification of low energy atoms interaction principles which is of utmost interest for quantum theory of scattering.

The purpose of this work is the research of cross sections and mechanisms of Ar(3p5 4p) atomic levels excitation at collision energies that correspond with the adiabatic approximation conditions.

SETUP AND MEASUREMENT PROCEDURE

The measurements of the cross sections at interaction of an atomic beam with a gas target were carried out by optical methods on a setup, controlled by computer [3].

The beam of neutral atoms was produced by means of charge exchange of Ar ions in its own gas

in extending electrode channels of an ion source. The density of the atom beam was defined by secondary electron emission from the detector surface. The dependence of the secondary emission coefficient on the energy of atoms was measured. The flux density of fast atoms in the collision chamber reached 1016 particle/(m2s). The angular divergence of the neutral beam did not exceed 3 × 10– 4 sr.

The target gas pressure in the collision chamber varied from 5 × 10– 2 to 2,5 × 10– 1 Pa, the residual gas pressure did not exceed 3 × 10– 4 Pa. The gas pressure at the ion source varied in the range 8 ÷ 15 Pa.

The investigated area was at 123 mm distance from the extending electrode of the fast particles source and at 12 mm distance from the atom beam detector inlet. The distance between the detector target electrode and its input aperture was equal to 47 mm. The scattering of particles from the beam was taken into account in determination of the flux density of fast atoms.

The emission of excited particles was observed at right angle to the atomic beam; therefore, radiating particles of the beam and the target were not distinguished. The analysis of polarization was implemented using the Glan – Taylor prism. The compensators from the quarter-wave mica plates were applied to remove the influence of polarizing effect of the optical monochromator.

The measurement procedure was described in detail in the work [3].

The emission cross section was directly measured in the experiment. Note that the emission cross section is determined by measuring the spectral line intensity, the flux density of fast atoms and target particle density [17].

Taking angular divergence of the dipole radiation into account, emission cross section is equal to

4 71 S ( Я ) G 1

О                           , ij Q K(X) IpNtL 1 + 7

where Ω – a solid angle, defined by the optical system aperture; S(λ) - photon count rate; K(λ) - absolute sensitivity of the registration system at the given wavelength; I_p - beam intensity of the fast particles; N_t - target particle density, and L - observation zone length. The coefficient G – shows the angular distribution of dipole emission:

G

3 P

3(1 P cos² О ) ,

where P - a degree of polarization, θ - an angle between a beam of fast particles and an optical axis of a system. The degree of polarization is determined by the following expression

P (I par Iper) /(I par Iper), where Ipar and Iper - intensities of components which are polarized in parallel and transversely to the beam of fast particles respectively. The value η takes into account a part of the excited fast atoms, which irradiate before leaving the observed zone. It is equal to

1 xLi exp( l/xi)(1 exp( L/xi)), where l – the distance between the entry point of fast particles in the collision chamber and the observation zone and xi=υτi, where υ – colliding particle velocity, τi - excited state life time. The multiplier 1/ (1+η) was obtained from the condition that excitation cross sections of fast and slow particles in symmetric collisions are equal.

The atom beam intensity in the observation zone was defined in the following way:

Ip

J eУ0(E)exp(аs(E)Ntd),

where J - detector current, e – charge of electron, γ⁰(E) - coefficient of secondary electron emission from the detector surface under the action of fast atoms, σ_s(E) - cross section of fast atoms reduction from atomic beam, а d - distance from the observation zone up to the detector surface.

While calculating the excitation cross sections the transition probabilities were taken from work [9], excited-states lifetimes – from [2].

RESULTS AND DISCUSSION

The excitation cross sections of Ar I 4p[3/2]₂, 4p′[3/2]₁, 4p′[1/2]₁ and 4p′[3/2]₂ levels and degree of polarization for 4s[3/2]⁰ ₂ – 4p[3/2]₂ and

4s[3/2]⁰ ₂ – 4p ′ [1/2]₁ transitions are represented in figures 1–4.

The statistical errors for the excitation cross sections and the polarization functions are represented in the figures (with probability of 95 %). The maximal estimate of systematic error could reach ±55 % when we take into account the inaccuracy of measurements of the absolute spectral sensitivity, the inaccuracy of the definition of the secondary electron yield from the detector surface of the fast particles, and the inaccuracy of the definition of the gas pressure of the target.

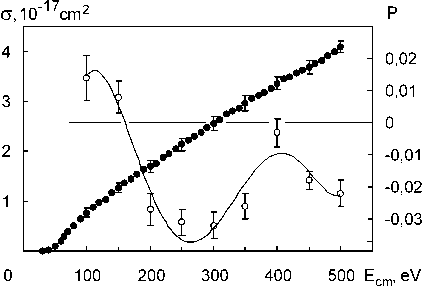
Fig. 1. Ar I 4p[3/2]₂ level excitation cross section (•) and degree of polarization for 4s[3/2]⁰ ₂ – 4p[3/2]₂ transition (о) plotted against collision energy of Ar atoms

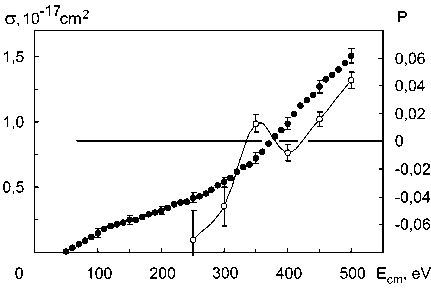
Fig. 3. Ar I 4p′[1/2]₁ level excitation cross section (•) and degree of polarization for 4s[3/2]⁰ ₂ – 4p′[1/2]₁ transition (о) plotted against collision energy of Ar atoms

ст,10"17ст2

О 100    200    300    400    500 Ест, eV

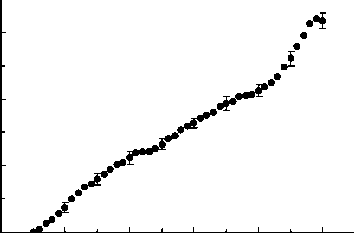
Fig. 2. Ar I 4p ′ [3/2]₁ level excitation cross section plotted against collision energy of Ar atoms

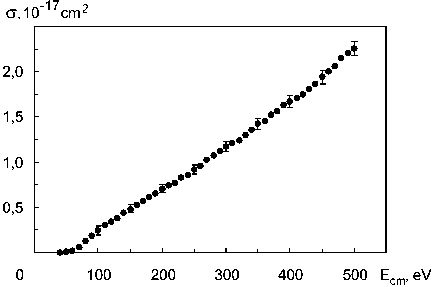
Fig. 4. Ar I 4p′[3/2]2 level excitation cross section plotted against collision energy of Ar atoms

The obtained results demonstrate that the polarization degree of emission significantly depends on collision energy: when the latter goes up, the former changes its sign. The fact that the sign of the polarization degree changes with the interaction energy change, proves that the mechanism of level population changes too [6].

For instance, since the angular momentum of 4p ′ [1/2]₁ excitation level is equal to 1, the positive polarization degree shows that the magnetic sublevel σ ₀, which is zero momentum projection onto internuclear axis of the Ar₂ quasimolecule, is mostly populated. Negative polarization degree, in its turn, means that there is a dense population at magnetic sublevels σ ₁, corresponding to ±1 projections. Therefore, according to the data obtained, if collision energy is higher than 400 eV, the population at the mentioned above level is determined by Σ _g– Σ '_g transactions. If collision energy is equal to or lower than 300 eV, level population is determined by Σ _g – Π _g transactions due to radial coupling of even terms of the Ar₂ quasimolecule.

It is important to note that since output Σ _g terms of the quasimolecule are actually double excited terms, it can be assumed that the other interacting atom is excited too. This fact agrees with Wigner’s law (system spin unchanged at collision) and with the research results described in works [14], [15].

The diabatic molecular orbital diagram for homo-nuclear system [5] and measurement results of the emission polarization lead to the following conclusion: if collision energy is less or equal to 300 eV, the population of 4p ′ [1/2]₁ level is determined by 4p σ – 4p π transactions due to rotational coupling at small nuclear distances. In case of higher energies, the population is governed by 5f σ – 5d σ transactions due to non-adiabatic radial coupling.

It is known (e. g. [1]), that at the interaction of atomic particles of the type

A+B^A+ B ^*( n )

the excitation cross section of the atomic particle at fixed collision energy σ ∼ n ^–3, where n is a main quantum number. However, the obtained data have allowed to make a conclusion that in this case the emission cross sections of Ar I in spectral series depend on the main quantum number as follows: σ ∼ n ^{– α} , where α characterizes serial dependence and varies from 12 up to 17. The values of α as a parameter of straight lines fitting ln σ ( n ) dependence in interval of main quantum numbers from 4 to 6 for a number of transitions are shown in table (large confidence intervals indicate that the dependence of ln σ ( n ) is non-linear).

The parameter α for transitions between Ar(3p5 4s) and Ar(3p5 n p) states (4 ≤ n ≤ 6) at 450 eV collision energy
Transitions	α
4s′[1/2] 1 0 – np′[1/2]0	12 ± 1
4s′[1/2] 0 0 – np′[1/2]1, 4s[3/2]0 2 – np[3/2]1, 4s [3/2]0 2 – np [3/2]2	14 ± 3
4s′[1/2] 0 0 – np′[3/2]1, 4s[3/2]0 2 – np[5/2]2	16 ± 3
4s [3/2] 1 0 – np [1/2]0, 4s[3/2]0 2 – np[5/2]3	17 ± 3

These results are in agreement with our data obtained earlier under similar conditions for the Ne I 2p⁵ 3p – 2p⁵ n d series (4 ≤ n ≤ 10) and 2p⁵ 3s – 2p⁵ n p series (3 ≤ n ≤ 8), and also with the data for He–He system [3, 4, 11–13]. Let us note that when n is small for helium α maximum value is 6, for neon it is 12 and for argon it reaches such values as 16–17. It is obvious from these data that at small n the value of α increases with the increase of the atomic mass and the number of atomic electrons of colliding atoms (figure 5).

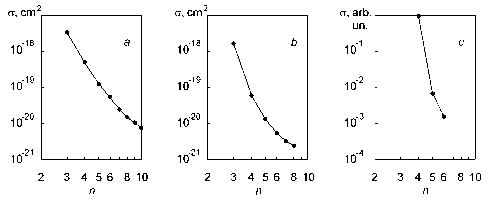
Fig. 5. The cross sections for He I 2¹S – n¹P (a), Ne I 3s[3/2] ₁ ⁰ – n p[3/2]₁ (b) and Ar I 4s′[1/2] ⁰ ₀ – n p′[3/2]₁, 4s[3/2]⁰ ₂ – n p[5/2]₂ ( c ) transitions at 450 eV collision energy plotted against main quantum number

ACKNOWLEDGMENTS

We would like to express our gratitude to the laboratory head I. P. Shibaev for support of this work as well as to A. S. Kashuba and A. S. Filatov.

* Работа поддержана Министерством образования РФ, программа «Научные и научно-педагогические кадры инновационной России» (проект № 14.В37.21.1066, № 14.В37.21.0755), и Программой стратегического развития (ПСР) ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012– 2016 гг.