Experimental Analysis of Xie and Kuek's Traffic Model with Handoff Scheme in Wireless Networks

Published Online February 2012 in MECS

The rapid growth in the demand for mobile communications has led to an intense research effort to achieve an efficient use of the scarce spectrum or channel allocated for cellular communications. Traffics (request and demand for service) in the wireless networks are ever increasing and are expected to be extremely non stationary [1][2]. The channel associated with the current connection serviced by a Base Stations (BS) is changed while a call is in progress. The Non Stationary Calls simply called Mobile Stations (MSs) are when away from the current BS (also called Mobile Ter min al, (MT)) the chances of Handoff [3] are increased. It is often initiated either by crossing a cell boundary or by deterioration in quality of the signal in the current channel. The existing call is then changed to a new nearest BS . Continuous service is achieved by supporting Handoff mechanism from one cell to the next adjacent cell as the MSs move through the coverage area is shown in Figure 1 below. We assume that every cell in the system is of the same size and has the same fixed number of channels. There are no guarded channels for Handoff calls in any cell, i.e., both new and Handoff calls have access to all the channels. Each MS is associated with a call at any given time. If a new call that is generated in a cell cannot find an idle channel in that cell, the call is discarded (blocked) immediately. An Handoff algorithm determines the dynamics of the MS which moves through the network. Therefore, Handoffs in a mobile cellular communications environment have become an increasingly important issue accommodating an increasingly large demand for services with simultaneous reduced cell sizes [3][4][5][6][7][8][9][10].

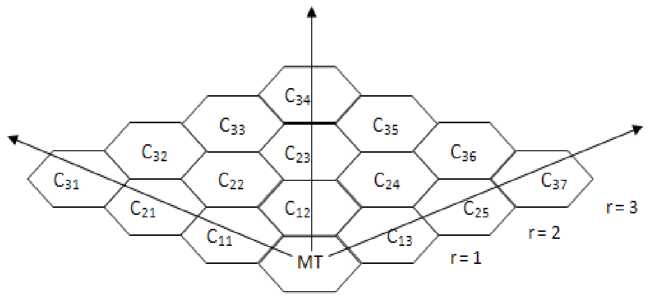
Figure 1. Same Column and Non-column Cellular Configuration for r = 3

In urban mobile cellular radio systems, especially when the cell size becomes relatively small, the Handoff mechanism has a significant impact on primary system performance criteria: Blocking probability of originating calls ( B O ) , Blocking probability of Handoff calls ( B H ) , and the forced termination probability of ongoing calls [3][8]. Before analyzing these performance criteria, it is important to establish a traffic model. In this paper we propose to modelling, implement and simulate the Xie and Kuek ' s Traffic Model [3] with Handoff behavior for mobile network. A simulation model EATM (Experimental Analysis of Traffic Model) with priority Handoff scheme is developed to investigate the Handoff performances. Simulation results show that measurement of blocking probabilities for both originating and Handoff calls is an impressive achievement of the model. In addition to this, the proposed model can increase Call Blocking Rate ( CBR ) as derived in [1][8][11][12] and shown in Equation (11) of Handoff calls.

2.    Proposed Work

Every cell in cellular network architecture (shown in Figure 1) is served by an underlying BS that is MT . BSs are connected together by using a wireless network. Figure 2(a) shows the fact that each hexagonal cell A, D, Q, P, X, Y, and Z are nothing but each MT . MSs generally move in the coverage area (each hexagon) similar to Figure 2 [13][14][15] and Table I [8] and when moving from a cell to another cell, Handoff occurs [3]. Movements may be made away from and/or towards the MT . h owever , movements away from the current MT is primarily responsible for Handoff to be taken place. For the time being suppose cell a in f igure 2(a) is our current BS . h owever , one-third of the coverage area of this BS is considered in this paper and equivalent to Figure 1.

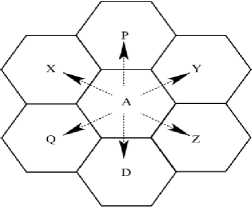
(a)

(b)

Figure 2. Mobility of Mobile Stations ( MSs )

When MSs move irrespective of the direction of movements in the cell of the current servicing BS then the following two cases and their corresponding sub cases [15] may arise: First, Call Acceptance - (a) A successful Handoff completion to the target cell, (b) New call arrival in the target cell, and (c) Active mobile terminal increases its resource demands. Second, Call Rejection - (a) A successful Handoff completion from the target cell. (b) Call termination in the target cell and (c) Active mobile terminal decreases its resource demands.

The current researches on Handoff mainly involve following two issues: (1) How does the Handoff process affect performance of wireless cellular system; (2) How do we design Handoff scheme so that channel resources are used efficiently and quality of service (QoS) is still guaranteed.

Recently, many analytical and simulation models have characterized the Handoff problems. Our approach provides high precise location and tracking of MTs by exploiting advanced traffic models. Some of these we have studied it in [1][7][8].

Table I: Generated Handoff Approaches

Approach	Movement of MSs w.r.t MT		Adjacent Level		Position of Cells Column
	Towards	Away from	Upper	Lower	Same Column	Not Same Column
I	N	Y	Y	N	Y	N
	Y	N	N	Y	Y	N
II	N	Y	Y	N	Y	N
	Y	N	N	Y	N	Y
III	N	Y	Y	N	N	Y
	Y	N	N	Y	Y	N
IV	N	Y	Y	N	N	Y
	Y	N	N	Y	N	Y

Here we have extended our work [16] with Xie and Kuek ' s Traffic Model [3]. Our approach EATM Model takes more advantages over previous models described in [1][7][8]. Major functionalities of the proposed model in this paper are organized in as follows:

First, we present an expression to Determine Arrival Rate ( λo ) of the calls followed by the expression of their Departure Rate ( µ ) Determination. Next, we choose a model through Traffic Model Selection. Next, we are going to implement a Priority Handoff Scheme. And last we have determined Call Blocking Rate of both originating calls and Handoff calls.

• 2.1    Determination of Arrival Rate

• 2.2    Determination of Departure Rate

• 2.3    Selection of Traffic Model

Number of MSs (also called Traffic Density [17]) varies location to location. And this location on the contrary affects arrival rate λo of originating calls from MSs to nearest BS ( MT ) . Likewise number of BSs varies. Assuming distance D [18][19] between two base stations is 1 km, λo [3] has been determined in S 2 BPQ model [16] as:

_{λ o =} Total Numberof Subscriber(S) in thatRegion ₍₁₎ Total Numberof MTs (X)

The departure rate µ (say, number of mobile stations get serviced in unit time) should be at least equal to arrival rate λo such that waiting for getting service becomes zero. Although in reality µ is much larger than λo . e xploiting p oison d istribution [17], with the traffic intensity factor ρ (defined as λo/µ ) lies between 0 and 1, departure rate µ has been established in S 2 BPQ Model [16] as:

0 ≤ λ o ≤ µ (2)

Every cell in cellular network architecture ( shown in f igure 1) is served by an underlying BS . e stablishment of a traffic model, in cellular system, is more imperative before analyzing the performance of the system [8][16]. Several traffic models [3][20] as well as different schemes [21][22][15][10] have been established on basis of making different assumptions about user mobility. o ne of them is the e xpected r ate of Handoff ( λ_H ) .

For our purpose Xie and Kuek ' s Traffic Model [3] shown in Equation (3) has been chosen as underlying implementation model with the assumption that the Arrival Rate of Handoff calls ( λ_H ) is determined by:

λ H = ∏ ( E [ c ], µ c - dwell )      (3)

Where,

E [ c ] = the average number of calls in a cell µc - dwell = the outgoing rate of mobile users

• 2.3.1    Determination of E[c]

For a maximum radial distance R _max (maximum distance from the current BS that provides services its MSs and after the distance an MS forcefully changes from current BS to another BS ) from the underlying network, total cells N under a BS is given by:

∑ R max (2 × r + 1)         (4)

r = 1

Average number of MSs we called here as Subscribers ( Subs ) , in any cell j at radial distance r (represented as Crj in Figure 1) is obtained by Equation (5):

Subs =

Total Number of MSs (S)

Total Number of Cells (N)

Let us consider average number of calls originated by a Sub ( MS ) is Calls Per Day Per Subscriber ( CPD ) . Thus,

E [ c ] = П ( ^Subs , CPD ) (6)

• 2.3.2    Determination of µc—dwell

Assuming that MSs move any one of the three directions - outwards, inwards and along the same radial level (shown in both Figure 1 and Figure 2) , the probability of MSs for simplicity moving outwards is one - third . Since, in every radial distance r <  R max , there are 2 x r + 1cells, thus, average number of calls going outwards (away from the current BS ) for N cells are given by:

Calls ( T ) = - Y R max Subs x CPD x (2 x r + 1)   (7)

• 3 ^ ^r = 1

Out of the total number of callers ( MSs ) going out from one radial level to the other, let us assume for the time being again one - third of them come back to the previous radial level. Therefore, total number of calls coming inwards (towards the underlying BS ) is:

Calls (Ф) = П(1Д   Calls (T))

Effective outgoing calls for the base station are therefore obtained by the Equation (9) as:

Effective Calls (T) = Calls (T) - Calls (Ф)(9)

Now, for Equation (3) we can compute the outgoing rate of mobile users’ pc - dwell and it is given by:

_J „ Effective   Calls( T )

pc - dwell =

Total Number of Cells (N)

• 2.4 . Priority Handoff Scheme

• 2.5    Determination of Call Blocking Rate

3.    Numerical Results

• 3.1    Observation I

An MS approaches cells from a cell with significant signal strength as priority set to Handoff requests by assigning channels S_R exclusively for Handoff calls out of S channels. Both originating calls and Handoff requests share the remaining S_C = S - S R channels. The blocking probabilities, B O for an originating call, and B_H of a Handoff request have been determined by Equations 1.22, and 1.23 in [3]

with the steady-state probabilities P (0) and P ( i ) at states "0" and " i "as expressed in Equations. 1.20 , and 1.21 in [3] respectively.

An MS when initiates a call generally expects to be serviced and enqueued in priority queue. Afterward a call gets serviced by its current MT taking advantage of Splay operations [16][23] on the Splay Tree [23] implementation of the priority queue followed by selection of the call from the tree using SIRO [16][17] queuing principle for providing service. At particular level r , 1 <  r <  R _max number of calls blocked i.e. Call Blocking Rate ( CBR_r ) can be decided by the Equation (11). This blocking does not mean discard of calls rather number calls gets serviced.

CBR r = 3 П ( ^R j , B o ,(2 x r + 1)) (11)

It is generally expected to be 90-100% so that the Call Dropping Rate ( CDR_r ) at a r <  R _max [1][8] is minimum as much as possible.

The parameters used for simulation are commonly used to analyze Handoff performance. Simulation of the suggested model has been performed in MATLAB Version 7.6.0.324 (R2008A). Numerical values of the fundamental parameters for Handoff initiation, arrival rate A O , and the departure rate p are based on COAI Report [24][25] for our beloved Megacity Kolkata. And they are set as A O = 1991 , and p = 2212 [13]. Exploiting these numerical values and inheriting necessary data from [16], all the Equations (3) through (10) and section 2.4 in this paper we have shown two observations.

Let us suppose that a mobile station makes at least 5 requests per day. Other values are shown in Table II. Graphical views of the Table II and followed by it, have been shown for the parameters A H , B O , and B H with varying radius (radial) distance in Figures 3 to 5 respectively.

Table II: Performance Metrics for Different Parameters at Radial Levels

Parameters	Outgoing Calls	Incoming Calls	Effective Calls	µ c	λ o	µ	P(0)	Average B o
	221.249	73.749	147.499	0.6584	22.885	25.427	0.2363	0.7636
λ h	29.26776 185.3625	48.77959 204.8743	68.29143 224.3861	87.80327   107.3151   126.8269   146.3388 243.898     263.4098   282.9216					165.8506
Bo	0.25456 0.82524	0.40729 0.86543	0.51639 0.9018	0.60124 0.935		0.67066 0.96555	0.72941 0.99383		0.78032 1.0202
B h	0.092985 0.3365	0.12777     0.16256 0.37129    0.40608		0.19735         0.23214 0.44087      0.47566			0.26693 0.51045		0.30172 0.54524

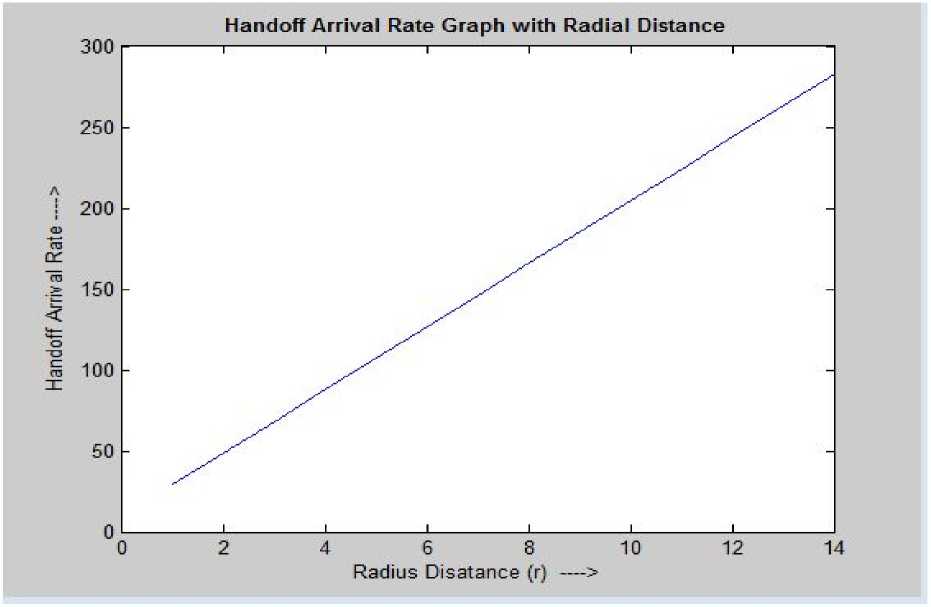
Figure 3. Handoff Arrival Rate vs. Radial Distance

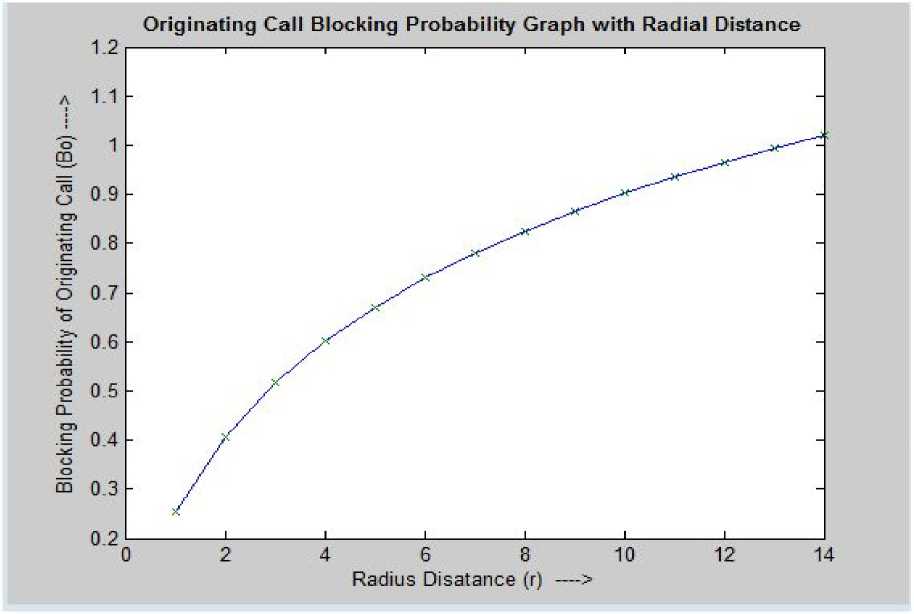
Figure 4. Blocking Probability of Originating Call vs. Radial Distance

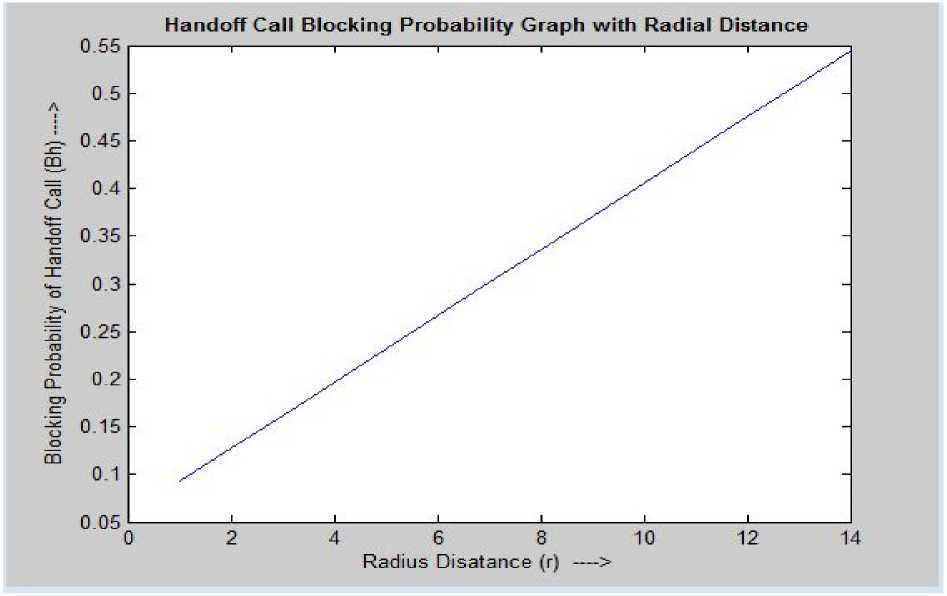
Figure 5. Blocking Probability of Handoff Call vs. Radial Distance

• 3.2    Observation II

Let us suppose that a mobile station makes at least 6 requests per day. Other values are shown in Table III. Similarly graphical views of the Table III and followed by it, have been shown for the parameters λH , BO , and BH with varying radius (radial) distance in Figures 6 to 8 respectively.

Table III: Performance Metrics for Different Parameters at Radial Levels

Parameters	Outgoing Calls	Incoming Calls	Effective Calls	µ c	λ o		µ	P(0)	Average B o
	221.2494	73.7498	147.4996	0.8779	26.546		29.496	0.1662	0.833
λ h	52.03157 294.8455	86.71928 329.5332	121.407 364.221	156.0947 398.9087		190.7824    225.4701 433.5964			260.1578
Bo	0.2779   0.44465   0.56375   0.65638   0.73217 0.94481      0.98451   1.0208   1.0541						0.79631	0.85189	0.90093
B h	0.18773 0.59019	0.24523 0.64768	0.30272 0.70517	0.36021 0.76267		0.41771		0.4752	0.53269

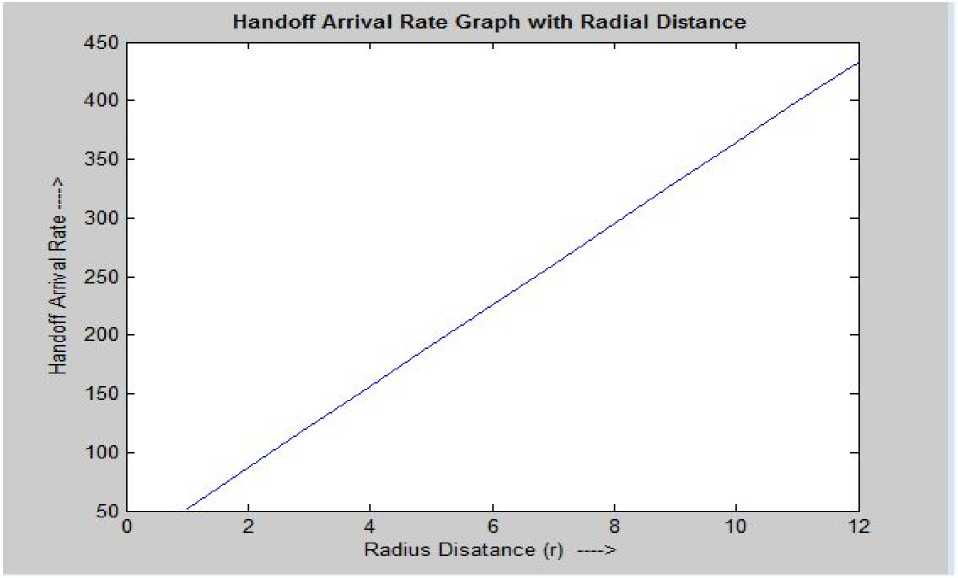
Figure 6. Handoff Arrival Rate vs. Radial Distance

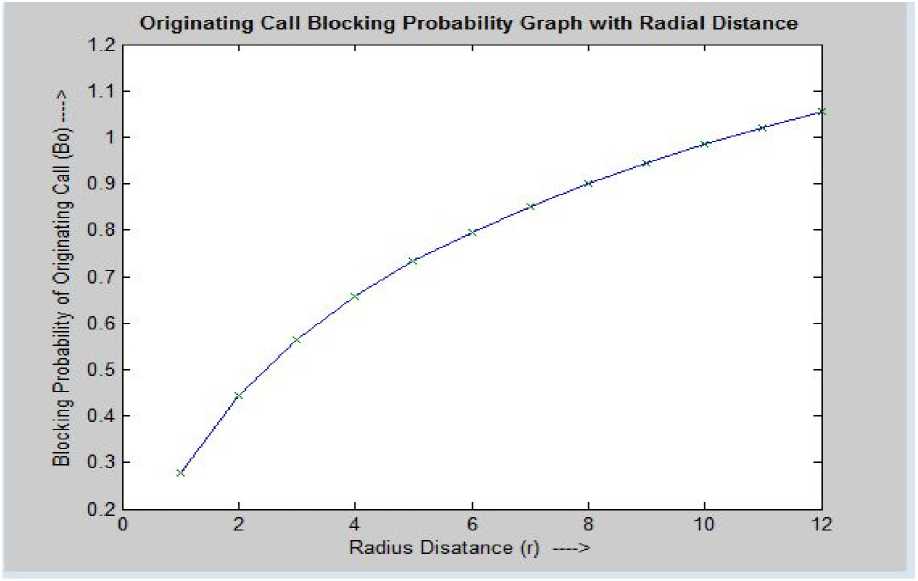
Figure 7. Blocking Probability of Originating Call vs. Radial Distance

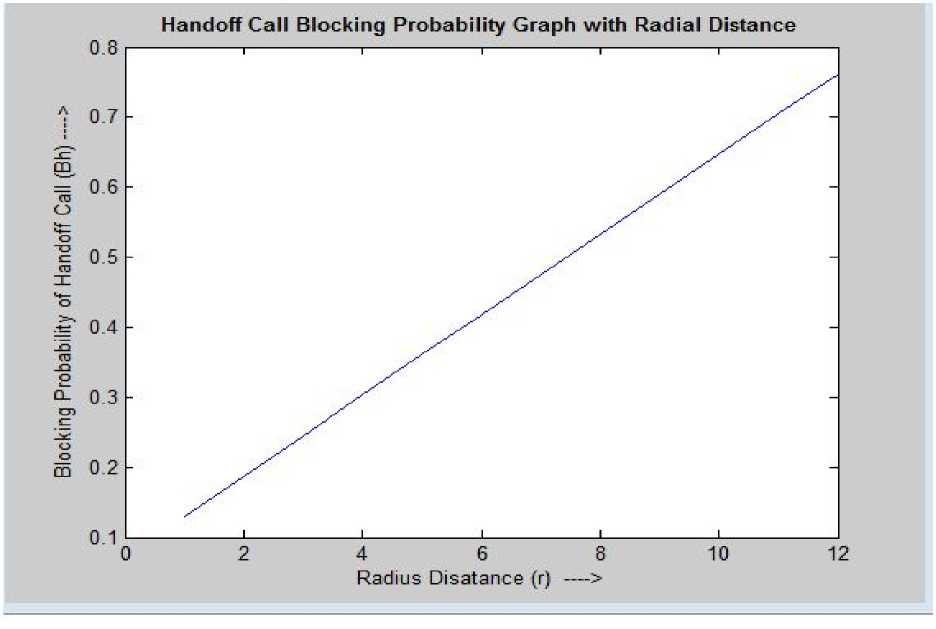
Figure 8. Blocking Probability of Handoff Call vs. Radial Distance

4.    Concluding Remarks

In this paper we claim that simulated results guarantee that our approach or the model described performs better like some existing algorithms for Handoff scheme. It is observed that increasing average number of calls per mobile station per day helps in improvement of the blocking probabilities for both originating calls and Handoff request calls. And these values are nearer to their actual values. Another achievement of the proposed model is working out of rate of blocked calls CBR , in addition. Although its behavior is not shown in this paper but similar job has been done in [1][8]. Simulation shows that CBR is increasing in nature with the increase in certain radial distance. After that increases slowly and saturates at r = Rmax . Surprisingly at r > Rmax it is decreasing in nature. It shows that a Handoff just occurred.

However, exact analytical models are difficult to define for the schemes, and if data traffic also needs to be incorporated, it becomes very difficult to have even an approximate model. This is an interesting topic that calls for further research.

Acknowledgements