Exploiting SIMD Instructions in Modern Microprocessors to Optimize the Performance of Stream Ciphers

Published Online May 2013 in MECS

Modern cryptographic protocols like TLS, SSL, etc. provide communication security by employing symmetric or secret key algorithms for encrypting the data and asymmetric or public key algorithms for key exchange. So, overall throughput of the communication system is largely influenced by throughput of the symmetric key algorithm used. Dedicated Stream cipher designs are more advantageous than block ciphers in counter mode, mainly in those areas where exceptionally high throughput is required. There is no doubt in the fact that the principal goal guiding the design of any stream cipher algorithm is security but along with that its performance matters a lot in real world applications, where data with high bit rate such as streaming video, streaming audio, VOIP, etc., has to be encrypted “on the fly”. By the advent of processor technology in desktop computers, the opportunity for improvement in software performance of cryptography algorithms has increased than ever.

The purpose of this paper is to discuss about the low-level software optimization techniques that can be achieved in latest desktop processors and how they should be applied in the design and implementation of stream ciphers. General design principles for using Single Instruction Multiple Data (SIMD) instructions are presented. Even though they are applicable to almost all modern Central Processing Units (CPU), specific attention has been given to INTEL CORE 2 processor family (core 2 duo, core 2 quad, etc.) and its further generations. Four stream cipher algorithms, namely, HC-128, Rabbit, Salsa 20/12 and Sosemanuk were thoroughly examined to show how they violate these optimization principles and which functions can be further efficiently implemented and how these optimizations improve the performance. All of them have been selected to the final portfolio of eSTREAM project which was meant for 'Stream ciphers for software applications with high throughput'. HC-128 and Rabbit ciphers are included in the latest release version of CyaSSL, a lightweight, open source embedded implementation of the SSL/TLS protocol. Rabbit is described in Internet draft RFC 4503 and it is also included in ISO/IEC 18033-4 [1].

Some of the cryptographic algorithms available now are not able to appreciate the optimization features of modern CPUs. Even when the algorithms are highly secure enough, some of the functions which are designed without considering the available performance optimizations, results in significant performance losses. Most of these performance issues could have been avoided in the design stage without impairing security. The main goal of this paper is to create greater awareness of these performance issues, so that the cryptographer can design an algorithm in such a way that, it efficiently makes use of the processing power available in modern processors.

The rest of the paper is arranged as follows. Section-II provides the general guidelines to be followed for optimizing a cryptographic algorithm. The principles to be followed while designing and implementing a stream cipher algorithm to efficiently incorporate MMX or SSE instructions have been discussed in section-III. In section-IV, the four eSTREAM final portfolio software stream ciphers are experimentally analyzed based on the guidelines presented and the performance improvement achieved is tabulated. Based on the experimental results, conclusions have been drawn and some recommendations for future work have been proposed in section-V.

• II.    Basic Optimization Principles

Optimization of a computer algorithm can be done at different stages viz. design level, source code level, compiler level and assembly level. Design level and source code level optimization of algorithms is a widely studied topic. Some general guidelines for cryptographic algorithm designers have been drawn out by Bruce Schneier et al. [2] which are enumerated below as seven statements.

• •    Conditional jumps have to be avoided whenever possible. INTEL processors from Pentium onwards has branch prediction capability and if a predicted branch from a conditional statement is wrong, penalty can be even greater than 12 clocks due to the flushing of pipeline.

• •    Loop unrolling can be done to reduce the number of jumps required for executing a function. Designer should take care to prevent formation of any dependencies between two consecutive iterations, which will otherwise cause pipeline stalls.

• •    Designer should try to use more numbers of less expensive RISC operations like addition, exclusive-OR, etc. than expensive instructions like multiply, divide, etc.

• •    Number of variables should be limited so that they will fit in the available registers.

• •    Size of the state tables, such as S-boxes, should be limited so that they will fit in CPU's on-chip data cache which is of size 32 KB per core for core 2 duo processor.

• •    In order to completely exploit the available pipelines and superscalar feature, algorithm should have parallelism.

• •    Table index must be computed as far ahead as possible before accessing tables, because it can avoid some penalty that will incur otherwise, between index calculation and table access.

Apart from these, some more basic optimizations can be made while implementing an algorithm.

• •    Some of the clock consuming functions can be implemented as inline assembly functions. Today, almost all compilers support inline assembly functions. It is true that there are highly optimizing compilers which can create faster assembly codes. The main advantage of inline assembly is that system specific instructions such as Multimedia Extension (MMX) and Streaming SIMD Extension (SSE) instructions can be incorporated along with general purpose instructions which will further enhance the performance of the algorithm. It also helps the programmer to reduce the number of jumps used in the implementation by removing the function calls.

• •    Instructions with different latencies but using the same stack of execution units should not be mixed together because it can cause write back bus conflicts when all of them needs the write back bus at the

same time. Write back bus conflicts can reduce the overall throughput [3].

• •    If instructions that uses different execution units are chosen then CPU pipelines can be efficiently utilized. For example, in core 2 duo processor add, shift and rotate instructions can simultaneously use three execution units and give the result in 1 clock cycle [4].

Performance of a well-designed cryptographic algorithm also depends upon the compiler used. As mentioned earlier, compiler level optimizations can be done which can even bring about more than 3 times increase in speed. Early in the history of compilers, compiler optimizations were not as good as hand-written ones. As compiler technologies have improved, good compilers can often generate better code than human programmers, and good post pass optimizers can improve highly hand-optimized code even further. Effect of compiler optimization on the four stream cipher algorithms compiled using GCC compiler is given in Table III.

• III. Advanced Optimization Techniques Using SIMD Instructions

In stream cipher algorithms, there will be a key-stream generating function which will be executed in each iteration. If that alone is implemented as inline assembly function, an observable amount of performance optimization can be achieved. Implementing the entire algorithm in assembly language can result in a significant increase in performance, but it is going to be a big burden for the programmer who is going to implement it for different platforms. Since present day compilers are so efficient in generating more optimized assembly codes than hand written ones, it will be a waste of labour to implement inline assembly functions with general purpose assembly instructions. Most of the modern microprocessors are supporting Single Instruction Multiple Data (SIMD) instructions which are vector instructions, operating in parallel on different data. Both INTEL and AMD microprocessors available today support MMX instruction set and SSE instruction set. MMX instructions process data stored in 64 bit MMX registers and SSE instructions process data stored in 128 bit XMM registers. When a general purpose instruction can process only one unit of 32 bit size at a time, MMX and SSE instructions can process two and four units, respectively. Therefore, incorporating these instructions in the inline assembly function can ultimately result in a code which is faster than the compiler optimized code. But before implementing an encryption algorithm using MMX or SSE instructions, certain issues have to be considered.

• i.        Possibility of Parallelism

• ii.      Availability of single MMX or SSE instruction

for realizing the operation.

• iii.      If the algorithm is implemented in such a way

that multiple MMX or SSE instructions are used to realize a single operation, then will it be faster than the compiler optimized code?

By using MMX or SSE instructions, software level parallelization of the algorithm is achieved. Therefore, in order to use these instructions, algorithm should be parallelizable. Since general design goal of an encryption algorithm is to maximize cascading of bits, it cannot be fully parallelized. Even then, it is possible to provide a limited amount of parallelizable operations in the algorithm without causing impairment to the security. Not all the general purpose instructions have equivalent MMX or SSE instructions. For example, rotation of the data inside MMX or XMM registers. In order to do rotation, three instructions – shift right, shift left and exclusive-OR – has to be executed, which will consume 3 cycles minimum instead of 1 cycle. If the operation used cannot be realized using a single XMM instruction then throughput may be either equal to or less than that of general purpose instruction. If only a few operations need multiple instructions and remaining can be executed in one clock cycle, then MMX or SSE instructions can be tried. Superscalar execution feature is available for many of the general purpose instructions where as it is rarely available for MMX or SSE instructions and most of the general purpose instructions are RISC instructions which have a very small latency and high throughput when compared with MMX or SSE instructions. Hence, if a significant amount of operations need multiple MMX or SSE instructions, then the code generated by an optimized compiler will surely overwhelm it. If special care is taken about certain aspects of MMX and SSE instructions while designing the stream cipher algorithm, then it can be implemented in a highly optimized way. Following are a few guidelines to be followed while designing and implementing a stream cipher algorithm in order to efficiently incorporate MMX or SSE instructions: • Algorithm should be vectorizable. There should not be any dependency between 128 bit input and corresponding 128 bit output of an SSE instruction. For example, if an operation gives 32 bit output in each i^th iteration and that output is feedback to the input of the same operation in i+1^th , i+2^th or i+3^th iteration, then this operation cannot be implemented efficiently using SSE instruction due to the dependency present between the input blocks and corresponding output blocks. The same principle is applicable for MMX instructions as well.

• •    128 bit memory accesses using SSE instructions will

be faster if it is a 16 byte aligned memory location. For aligned memory access MOVDQA instruction is used which has a latency of 2-3 clock cycles whereas for unaligned memory accesses MOVDQU instruction is used which has a latency of 2-8 clock cycles. It won’t be always possible to design an algorithm which restricts memory accesses to aligned locations but it can be made possible by applying some tweaks during implementation [3].

• •    Rotations are time-consuming if rotation length is not a multiple of eight. Since a dedicated rotation instruction is not present in MMX or SSE instruction

set, implementation of rotation operations using them can reduce the efficiency. Therefore it will be always better to replace such operations with something else while designing the algorithm after making sure that replacement is not going to cause any kind of security flaws. Newer versions of core microarchitecture processors supports PSHUFB (Packed Shuffle Bytes) instruction which is meant for shuffling the byte values stored in an MMX or XMM register. This can be used for performing packed rotations of the data, where the number of bit positions to be rotated is eight or multiples of eight. Whereas in the original Core 2 (Conroe) architecture PSHUFB takes 4 micro ops to complete, Penryn architecture introduced a dedicated shuffle unit which allows it to complete in just 1 micro ops. The Core i7 (Nehalem) architecture has 2 of these shuffle units, allowing 2 PSHUFB instructions to be executed per cycle [4]. Hence, algorithms which are designed with eight bit or multiples of eight bit rotations can be efficiently implemented using MMX or SSE instruction set.

• •    Look up tables should be used only if it is unavoidable. Accessing look up tables cannot be efficiently implemented using MMX or SSE instructions because if each table entry is of 32 bit size and independent of each other, then two or four table accesses are required to fill the MMX register and XMM register, respectively.

• •    Always use faster and least number of instructions while implementing an operation which cannot be implemented using a single instruction. Normally, more than one option will be available for implementing an operation and to select the best one, programmer should be aware of all MMX and SSE instructions and their clock cycle requirement. For example, to move low order double words of registers MM0 and MM1 to a single register MM1, two ways can be adopted. These two methods are given below and among them the second one with 1 clock cycle latency is preferred over the first one with 2 clock cycle latency in a core 2 duo processor [4].

  Method 1	Method 2
  psllq mm0,32 por mm1,mm0	punpckldq mm1,mm0

• •    Always use MOVDQA instruction for copying an entire array to another. Since it can complete a 128 bit memory read and write in 5 cycles compared to the 5 cycles taken by the MOV instruction for a 32 bit memory read and write [4], a four-fold increase in speed of the copying operation can be achieved.

• IV.    Analysis of eSTREAM Algorithms

In this section, the four eSTREAM final portfolio software stream ciphers, namely, HC-128, Rabbit, Salsa

20/12 and Sosemanuk are analyzed in terms of the guidelines presented above. This scrutiny is not meant to question the efficiency of these algorithms, but rather to provide some practical examples about the general principles to be followed to efficiently design and implement a stream cipher algorithm. Only the key portions of inner loops, such as, key-stream generation function and initialization function are examined. Optimization of the algorithms using SIMD instructions is the main topic of analysis and feasibility of implementing each function using these instructions is studied. Performance improvement achieved by the stream ciphers using these techniques on an INTEL core 2 duo processor is also listed at the end of this section.

• A.    HC-128

HC-128 [5] is a software stream cipher designed by Hongjun Wu. This cipher makes use of a 128-bit key and 128-bit initialization vector. Its secret state consists of two tables, each with 512 32-bit elements and at each step one element of one of the tables is updated using a non-linear feedback function, while one 32-bit output is generated from the non-linear output filtering function. There are two main functions in HC-128 algorithm – table updating function used in the initialization process and output generation plus table updating function used in key-stream generation process. C implementation of these functions is shown below:

/*h1 function*/

#define h1 (ctx, x, y) {\ char a,c;\ a = (char) (x);\ c = (char) ((x) >> 16); \ y = (ctx->T[512+a])+(ctx->T[512+256+c]); }\

/*update P and generate 32 bits keystream*/

#define step_P(ctx,u,v,a,b,c,d,n) {\ unsigned long tem0,tem1 ,tem2,tem3;\ h1((ctx),(ctx->X[(d)]),tem3);\ tem0=rotr((ctx->T[(v)]),23);\ tem1=rotr((ctx->X[(c)]),10);\ tem2=rotr((ctx->X[(b)]),8);\

(ctx->T[(u)]) += tem2+(tem0 ^ tem1); \

(ctx->X[(a)]) = (ctx->T[(u)]);\

• (n) = tem3 ^ (ctx->T[(u)]) ;} \

void generate_keystream(ECRYPT_ctx* ctx, u32* keystream) {/* some operations are here*/ if (ctx->counter1024 < 512){ ctx->counter1024=(ctx->counter1024 + 16) &0x3ff; step_P(ctx, cc+0, cc+1, 0, 6, 13,4, keystream[0]);

step_P(ctx, cc+1, cc+2, 1, 7, 14,5, keystream[1]);

step_P(ctx, cc+2, cc+3, 2, 8, 15,6, keystream[2]);

step_P(ctx, cc+3, cc+4, 3, 9, 0,7, keystream[3]);

step _ P(ctx, cc+15,dd+0, 15,5, 12,3, keystream[15]); }}

• H. Wu designed HC-128 in such a way that dependency between operations is very small (for e.g. 3 rotation operations performed in each step are independent of each other) and so it is suitable for modern superscalar processors. He has also given an optimized code in which loop unrolling is used and only one branch decision is made for every 16 steps. Key generation function can be efficiently implemented in a high level language like C

with an optimized compiler and it offers a very impressive performance to encrypt large streams of data. The main drawback of HC-128 is its time-consuming initialization process.

Since all 16 steps in the key generation function are the same with inputs having a regular order, it is possible to implement the step_P macro using SIMD instructions. If MMX instructions are used, then each step_P macro can generate 64 bit output key-stream at an instant and if SSE instructions are used, then 128 bit output key-stream can be generated at an instant. The step_P macro has to be analyzed to identify if there is any operation in it which cannot be directly implemented using MMX or SSE instructions. In h1 macro, two byte values obtained from the input x is used as a pointer to the two locations in P-table and sum of the contents of those locations is given as the output. In MMX or SSE instruction set, there are no instructions to perform this table access in a single step for four different values of input x . Therefore, h1 macro has to be implemented using general purpose instructions and its outputs have to be moved to an MMX or XMM register. All the arrays used, like the secret table T , buffer table X & Y and key-stream array can be aligned to 16 byte memory locations to make the memory access using SSE instruction faster. If step_P macro is implemented using SSE, then instead of 16 macro calls only 4 calls are needed.

step_P(ctx, cc+0, cc+1, 0, 6, 13,4, keystream[0]); step_P(ctx, cc+4, cc+5, 4, 10, 1,8, keystream[4]); step_P(ctx, cc+8, cc+9, 8, 14, 5,12, keystream[8]); step_P(ctx, cc+12, cc+13, 12, 2, 9,0, keystream[12]);

Some of the inputs to the macro step_P(ctx,u,v,a,b,c,d,n) are not aligned to a 16 byte memory location. Inputs u, a & d used in these four steps are pointing to 16 byte aligned memory locations where as remaining inputs v, c & b are not. Therefore, memory accesses corresponding to these nonaligned inputs will reduce the efficiency. This issue can be solved to some extend by making a few changes in the macro definition and inputs. Since memory pointed by the input variables u & v have 12 overlapping bytes, unaligned input variable v can be avoided. Remaining 4 bytes of variable v can be accessed using a general purpose instruction and all of them can be merged into an XMM register. Likewise, by limiting the values given to the inputs a, b, c & d to 0, 4, 8 or 12, they can be made to point to 16 byte aligned memory locations. Modified macro calls are shown below:

step_P(ctx, cc+0, 0, 4, 8,12, keystream[0]);

step_P(ctx, cc+4, 4, 8, 12,0, keystream[4]);

step_P(ctx, cc+8, 8, 12, 0,4, keystream[8]);

step_P(ctx, cc+12, 12, 0, 4,8, keystream[12]);

All these issues and implementation techniques work well for update function also. Due to the above mentioned issues, MMX implementation of HC-128 didn't show much improvement in performance but SSE implementation outperformed the compiler-optimized C implementation of HC-128. In a similar manner, SSE implementation of the initialization function is also providing an impressive performance enhancement in the encryption of packet data. From a design standpoint, it would have been better to have the feedback between ith step and i+5th step instead of ith step and i+4th step. This would have improved the performance of the algorithm by a fairly good amount. Also, out of the three rotations two of them could have been multiple of byte rotations. It is possible that some of these proposed changes might raise some security issues. If cryptanalytic studies can prove that algorithm is still secure with such changes then encryption speed of the modified algorithm will be improved significantly by implementing it using SIMD instructions.

• B.    Rabbit

Rabbit [6] is a high speed stream cipher designed by Martin Boesgaard, et al. It uses a 128-bit key and a 64-bit initialization vector. In each iteration an output block of 128 pseudo-random bits from a combination of the internal state bits are generated. The size of the internal state is 513 bits divided between eight 32-bit state variables, eight 32-bit counters and one counter carry bit. The eight state variables are updated by eight coupled non-linear functions based on simple arithmetic and other basic operations such as rotation. C implementation of the state updating function is given below:

static unsigned long RABBIT_g_func(unsigned long x) { unsigned long a, b, h, l;

a = x & 0xFFFF;

b = x>>16;

h = ((((a*a)>>17) + (a*b))>>15) + b*b;

l = x*x;

return (h^l);           } static void RABBIT_next_state(RABBIT_ctx *p_instance) { unsigned long g[8], c_old[8], i;

/* some operations are here*/ for (i=0;i<8;i++)

{                                                             g[i] =

RABBIT_g_func((p_instance->x[i] + p_instance->c[i])); }/*

Calculate new state values */ p_instance->x[0] = (g[0] + ROTL32(g[7],16) + ROTL32(g[6],16));

p_instance->x[1] = (g[1] + ROTL32(g[0], 8) + g[7]);

p_instance->x[2] = (g[2] + ROTL32(g[1],16) + ROTL32(g[0], 16));

p_instance->x[3] = (g[3] + ROTL32(g[2], 8) + g[1]);

p_instance->x[4] = (g[4] + ROTL32(g[3],16) + ROTL32(g[2], 16));

p_instance->x[5] = (g[5] + ROTL32(g[4], 8) + g[3]);

p_instance->x[6] = (g[6] + ROTL32(g[5],16) + ROTL32(g[4], 16));

p_instance->x[7] = (g[7] + ROTL32(g[6], 8) + g[5]);  }

Rabbit was among the most efficient stream ciphers submitted to the eSTREAM project and it was designed to be faster than most of the commonly used ciphers. In this stream cipher, major part of the key generation function is made of addition operation and complicated table accesses are absent. Therefore, it can be efficiently implemented in modern superscalar processors using an optimized compiler. Rabbit's inner loop has a counter updating function which is made of simple additions with carry. Addition operation can be efficiently implemented using the general purpose instruction ADD which has superscalar execution units. Since carry from one step has to be added to the other, MMX instructions cannot be used for efficient implementation. Absence of double quad word addition (four steps of addition with carry can be implemented in a single step) in SSE instruction set prevents the use of SSE instructions to improve the performance of counter updating function. Due to all these reasons, it was concluded that it is better to implement counter updating using general purpose instructions.

State updating is the most time-consuming part of the key generation loop. Totally 12 rotations are present in a single iteration and since rotations are clock consuming operations, this part of the key generation loop cannot be optimized using general purpose instructions. From the code given above, it can be observed that all the even steps are performing one type of operation and odd steps are performing another type. There are four steps each in both group and hence, it is possible to implement this function using MMX or SSE instructions. Before implementing it using SSE instructions, all the arrays used such as g & X , should be pointing to a 16 byte aligned memory location. Inputs to the even steps and inputs to the odd steps should be arranged in separate XMM registers, so that instead of 8 steps, function can be completed in two steps.

p_instance->x[e] = (g[e] + ROTL32 (g[],16) + ROTL32(g[], 16));

p_instance->x[o] = (g[o] + ROTL32(g[], 8) + g[]);

Another best feature of Rabbit design is that all the rotations are multiple of byte rotations – 8 bit and 16 bit. Therefore PSHUFB instruction can be used to rotate four

double words in one clock cycle which will ideally save 9 clock cycles in each iteration and result in a significant increase in the performance of the cipher. Same approach can be also used for implementing it using MMX instructions but performance increase will be only half that of SSE implementation. Therefore it is preferred to use SSE instructions. In short, from the design standpoint, Rabbit is a well-designed algorithm in which a fairly good amount of optimizations can be made to make it an even faster cipher.

• C.    Salsa 20/12

Salsa 20/12 [7] is a software-oriented stream cipher designed by Bernstein. During the operation of the cipher the key, a 64-bit nonce (unique message number), a 64-bit counter, and four 32-bit constants are used to construct the 512-bit initial state of the cipher. After 12 iterations of the Salsa 20/12 round function, the updated state is used as a 512-bit output. Each such output block is an independent combination of the key, nonce, and counter and, since there is no chaining between blocks, the operation of Salsa20/12 resembles the operation of a block cipher in counter mode. Salsa20/12 therefore shares the very same implementation advantages, in particular, the ability to generate output blocks in any order and in parallel. The round transformation of Salsa uses a combination of three simple operations: addition modulo 232, bit rotation and bitwise exclusive-OR (what has since become known as an ARX construction). C implementation of the key generation function of Salsa 20/12 is given below:

static void salsa20_wordtobyte(char output[64], long input[16]) { for (i = 0;i < 16;++i) x[i] = input[i];

for (i = 12;i > 0;i -= 2) {

x[ 4] = XOR(x[ 4],ROTATE(PLUS(x[ 0],x[12]), 7));

x[ 8] = XOR(x[ 8],ROTATE(PLUS(x[ 4],x[ 0]), 9));

x[12] = XOR(x[12],ROTATE(PLUS(x[ 8],x[ 4]),13));

x[ 0] = XOR(x[ 0],ROTATE(PLUS(x[12],x[ 8]),18));

x[ 1] = XOR(x[ 1],ROTATE(PLUS(x[ 0],x[ 3]), 7)); x[ 2] = XOR(x[ 2],ROTATE(PLUS(x[ 1],x[ 0]), 9)); x[ 3] = XOR(x[ 3],ROTATE(PLUS(x[ 2],x[ 1]),13)); x[ 0] = XOR(x[ 0],ROTATE(PLUS(x[ 3],x[ 2]),18)); x[ 6] = XOR(x[ 6],ROTATE(PLUS(x[ 5],x[ 4]), 7));

x[10] = XOR(x[10],ROTATE(PLUS(x[ 9],x[ 8]),18));

x[12] = XOR(x[12],ROTATE(PLUS(x[15],x[14]), 7));

x[13] = XOR(x[13],ROTATE(PLUS(x[12],x[15]), 9));

x[14] = XOR(x[14],ROTATE(PLUS(x[13],x[12]),13));

x[15] = XOR(x[15],ROTATE(PLUS(x[14],x[13]),18)); } for (i = 0;i < 16;++i) x[i] = PLUS(x[i],input[i]);

for (i = 0;i < 16;++i) U32TO8_LITTLE(output + 4 * i, x[i]);  }

Old location	New location
X[0] X[1] X[2] X[3] X[4] X[5] X[6] X[7] X[8] X[9] X[10] X[11] X[12] X[13] X[14] X[15]	X[12] X[9] X[6] X[3] X[0] X[13] X[10] X[7] X[4] X[1] X[14] X[11] X[8] X[5] X[2] X[15]

After completing 12 iterations, following inverse operation of the above mapping has to be done to generate the output.

for (i = 0;i < 4;i++)    { output[4*i]=x[(12+(4*i))%16];

output[4*i+1]=x[(9+(4*i))%16];

output[4*i+2]=x[(6+(4*i))%16];

output[4*i+3]=x[3+(4*i)];   }

All the above data structure restructuring operations create an overhead on the encryption speed which was experimentally measured to be 0.7 cycles per byte. Even though the above method of rearranging elements of the state table doesn’t completely eliminate the need for shuffling elements within a register, it helps in efficiently implementing Salsa 20/12 using SIMD instructions. In spite of giving special attention on performance while designing this algorithm, it has a drawback (which cannot be considered as a drawback from security point of view). There are four types of rotations in Salsa key generation function and none of them are having a byte or multiples of byte rotation distance. If at least one or two of them had multiples of byte rotation distance, performance would have been much more increased while using SIMD instructions.

• D.    Sosemanuk

Sosemanuk [8] is a stream cipher developed by Come Berbain, et al. It has a variable key length, ranging from 128 to 256 bits, and takes an initial value of 128 bits. It uses design principles similar to the stream cipher SNOW 2.0 and the block cipher SERPENT. Sosemanuk aims to fix some potential structural weaknesses in SNOW 2.0 while providing better performance by decreasing the size of the internal state. As for SNOW 2.0, Sosemanuk has two main components: a linear feedback shift register (LFSR) and a finite state machine (FSM). The LFSR operates on 32-bit words and has length 10. At every clock a new 32-bit word is computed. The FSM has two 32-bit memory registers. At each step the FSM takes as input some words from the LFSR, updates the memory registers, and produces a 32-bit output. On every four consecutive output words from the FSM, an output transformation, based on SERPENT, is applied. The resulting four 32-bit output words are exclusive-ORed with four outputs from the LFSR to produce four 32-bit words of key-stream. The relevant portion of the key generation loop is given below:

static void sosemanuk_internal (sosemanuk_run_context *rc) { #define MUL_A(x) (u32)(((x) << 8 ) ^ mul_a[(x) >> 24]) #define MUL_G(x) (((x) >> 8) ^ mul_ia[(x) \ tt = XMUX(r1, s ## x1, s ## x8); \ or1 = r1; r1 = (u32)(r2 + tt); \ tt = (u32)(or1 * 0x54655307); r2 = ROTL(tt, 7); \

} while (0)

#define LRU(x0, x1, x2, x3, x4, x5, x6, x7, x8, x9, dd) do { \ dd = s ## x0; \ s ## x0 = MUL_A(s ## x0) ^ MUL_G(s ## x3) ^ s ## x9; \

} while (0)

#define CC1(x0, x1, x2, x3, x4, x5, x6, x7, x8, x9, ee) do { \ ee = (u32)(s ## x9 + r1) ^ r2; \

} while (0)

#define STEP(x0, x1, x2, x3, x4, x5, x6, x7, x8, x9, dd, ee) do { \ FSM(x0, x1, x2, x3, x4, x5, x6, x7, x8, x9); \ LRU(x0, x1, x2, x3, x4, x5, x6, x7, x8, x9, dd); \ CC1(x0, x1, x2, x3, x4, x5, x6, x7, x8, x9, ee); \ } while (0)

/* some more operations are here */

STEP(00, 01, 02, 03, 04, 05, 06, 07, 08, 09, v0, u0);

STEP(09, 00, 01, 02, 03, 04, 05, 06, 07, 08, v3, u3);

SRD(S2, 2, 3, 1, 4, 64);

/* some more operations are here */  }

Sosemanuk was designed in such a way that it could be efficiently implemented in most of the platforms. LFSR length was chosen as 10 for efficient implementation. Designers of the cipher anticipated that physical shifting of the LFSR is going to be an inefficient process and to improve the performance, a few number of steps, which is equal to a multiple of the LFSR length, have to be rolled back. Since, a 128 bit key-stream output is generated only after four consecutive shifts of the

LFSR, at least 20 steps of the LFSR operation has to be unrolled. This implementation enhanced the performance of LFSR operation. The selection of the fastest serpent S-box (S 2 ) for output transformation was also meant for improving the performance.

Despite having these many features to increase the efficiency, Sosemanuk have some design deficiencies which prevent it from getting parallelized. Since only after 4 LFSR shifts one key-stream output is generated, it will be better to implement these 4 shifts in a single step using SSE instructions. This will be possible only if finite state machine supports parallelization. For this purpose, STEP function has to be analyzed. It consists of 3 macros viz. FSM, LRU, CC1. FSM updates the 32 bit finite state machine registers r 1 & r 2 in a sequential manner, i.e. new value of r 1 depends on old value of r 1 & r 2 and new value of r 2 depends on old value of r 1 . Existence of this dependency feature prevents use of SIMD instructions for implementing FSM . LRU updates the linear feedback shift register based on a complex feedback polynomial. In order to implement it, two lookup tables, namely mul_a & mul_ia , are used. The t^th and t+3^rd elements from the LFSR are used to point towards an element in the corresponding look up table. As mentioned earlier, look up table accesses cannot be efficiently implemented using SIMD instructions because each 32 bit value point towards a different location. Hence, it becomes an infeasible task to efficiently implement LRU macro using SIMD instructions. CC1 is a combination function used to combine the new states of LFSR and FSM and therefore, it is inappropriate to consider the parallelization of this function when process of updating LFSR and FSM are not parallelizable. Gladman [9] has implemented Serpent S-boxes using MMX instructions which allows two blocks to be processed in parallel. This implementation can be used for performing output transformations and also in the initialization process. This is the only parallelization possible for Sosemanuk algorithm and the proportion of parallelization performed is too small to observe any substantial improvement in performance.

• E.    Experimental Results

  In order to validate the theoretical studies, performance of all the four stream ciphers were tested in a Core 2 Duo processor platform. Read Time Stamp Counter (RDTSC) instruction [10] was used to measure the exact number of clock cycles consumed by each algorithm for generating a byte of the key-stream. Four different modes of encryption were tested based on the size of the data to be encrypted, which are long stream (LS) data, 40 Byte data packets, 576 Byte data packets and 1500 Byte data packets. In long stream data encryption mode 4096 bytes of data are encrypted after a single key and IV initialization whereas in packet encryption mode for each packet a new IV initialization is performed. Therefore, encryption of packet data depends on the efficiency of both key-stream generation and IV initialization process. Except Sosemanuk, all other algorithms were implemented using SSE instructions inside inline assembly functions and the

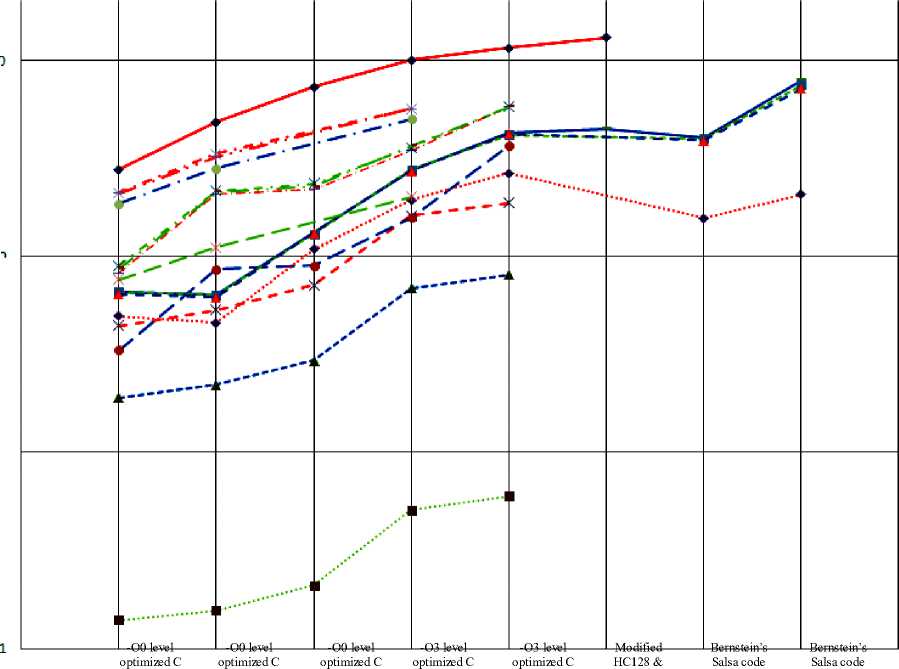
performance improvements were calculated. Encryption speed achieved by various implementations of the four eSTREAM stream ciphers when compiled using GCC compiler under –O0 level compiler optimization is tabulated in Table I. In order to demonstrate the effect of compiler optimization, these implementations were again tested using GCC compiler under –O3 level compiler optimization and the result obtained is given in Table III. A different set of implementations of Salsa20/12 stream cipher by Bernstein is available under eSTREAM submission list. It has been implemented using a new programming tool named qhasm which is used for implementing high speed computations in much easier manner than assembly language programming. Performances of two of these implementations were also tested and are given in Table IV. In the above subsections some modifications to the algorithms for improving their speed were suggested. Modified versions of HC-128 stream cipher and Salsa20/12 stream cipher were implemented and tested. These results are tabulated in Table V. In order to have a better comprehension of all these performance results, they were plotted in a graph and it is shown in Figure 1. System specifications are given in Table II.

TABLE I. E ncryption S peed of e STREAM C iphers in C ycles / B yte with –O0 L evel C ompiler O ptimization

Algorithm	Basic C code				C Code with inline General assembly				C Code with inline SSE instructions				% gain in cycles for LS encryption
	LS	40B	576B	1500B	LS	40B	576B	1500B	LS	40B	576B	1500B
HC-128	10.8	2145	157.7	67.6	6.2	1916.4	135.7	56.2	4.1	1429	102.2	41.9	62%
Rabbit	33.5	90.2	36.7	34.7	13.9	34.8	14.5	14.1	12.8	33.5	13.6	13.2	61.8%
Salsa20/12*	45.7	60.6	45.3	46.7	47.2	65.6	47.2	48.5	22.8	27.5	23	22.8	50.1%
Sosemanuk*	14.2	39.4	16.2	14.3	9	27	10.7	9.3	x	x	x	x	36.6%

TABLE II. System Specification

Processor - INTEL Core 2 Duo E8400 Clock frequency - 3 GHz RAM – 2 GB

Compiler - GCC version 4.6.1

TABLE III. Encryption Speed of eSTREAM Ciphers in Cycles / Byte with –O3 Level Compiler Optimization

Algorithm	Basic C code				C Code with inline SSE instructions				% gain in cycles for LS encryption
	LS	40B	576B	1500B	LS	40B	576B	1500B
HC-128	3	591.3	43.7	18.6	2.6	500.4	37.1	16	13.33%
Rabbit	8.4	19	8.6	8.2	5.2	8.2	5.2	5.2	38%
Salsa 20/12*	11	15.5	10.8	11	7	11.3	7.2	7.1	36.4%
Sosemanuk*	5.3	14.9	6	5.3	x	x	x	x	x

TABLE IV. Encryption Speed of Bernstein’S Implementation of Salsa20/12* in Cycles / Byte

	Code with x86 instructions	Code with SSE instructions
LS	7.4	3.8
40B	19.2	14.5
576B	7.5	4
1500B	7.7	4.2
% gain in cycles for LS encryption	48%

—*— HC12B (IS)

- Ж- Rabbit (LS)

-------Sa Isa 20/12 (LS)

— K— Sosemanuk (LS)

■ - HC12B (40B)

—e— Rabbit (40B)

■■ Sa Isa 20/12 (40 B)

— Sosemanuk (40B)

-*— HC123 (576B)

- Rabbit (576B)

—■ --Salsa20/12 (576B)

—•■ - Sosemanuk (576B)

- № - HC12B (15OOB)

---- Rabbit (1500B)

- * ~Salsa20/12 (1500B)

---1-- ■ Sosemanuk (1500B)

LOGO

Encryption speed in MB/s

Code

Salsa20/12

code

Code with inlined General assembly

Code with inlined SSE instructions

Code with inlined SSE instructions with x86 instructions with SSE instructions

Algorithm	Modifications	Encryption speed for LS data (cycles/byte)
HC-128	a.         All rotation lengths were converted to multiple of 8. b.         Feedback between ith step and i+4th step was removed and a new feedback loop between ith and i+5th step was established.	2.3
Salsa20/12*	Two of the four rotation lengths were converted to multiple of 8.	6.7

* Tested using 256 bit key

Tested Implementations

Figure 1: Encryption speed of various implementations of eSTREAM ciphers in Megabytes/sec.

• V.    Conclusions

The test results given above have proven that SIMD implementations can improve the performance of an encryption algorithm. HC-128 was able to cross the 1 GB/s encryption speed limit using SSE instruction set. But the extent to which efficiency enhancement can be achieved depends upon the design of the algorithm. For example, HC-128 could achieve only 13.33% performance improvement whereas Rabbit and Salsa 20/12 achieved 38% and 36.4%, respectively. In Bernstein’s implementations, SSE version of Salsa20/12 achieved a 48% gain in speed. Another significant result was that the SSE implementation of Rabbit could overwhelm Sosemanuk in speed. We also achieved significant improvement in the performance of packet data encryption. 40 byte, 576 byte and 1500 byte packet encryption using HC-128 could save 91 clocks per byte, 6.6 clocks per byte and 2.6 clocks per byte, respectively.

The modifications done on HC128 and Salsa20/12 algorithms resulted in gaining 0.3 cycles per byte but it is undesirable to make changes in the design of an encryption algorithm after performing security analysis. Therefore, it is better to consider both security and efficiency while designing the algorithm. The designer should have a thorough knowledge about the computer architecture for which he is designing the algorithm and the general optimization principles must be kept in mind. Algorithm should be designed in such a way to exploit the processing power of a computer to its maximum. It should be parallelizable to a fair extend without impairing any security feature. Thus, fast encryption systems with a high quantum of security strength can be developed.

In this paper, all implementations were based on 32 bit architecture and the processing power of only a single core was utilized. But today 64 bit multicore processors are very popular. Both Intel’s and AMD’s x86-64 architecture support Advanced Vector Extensions (AVX) which offer 256 bit YMM registers to handle SIMD operations [10]. Hence, the level of vectorization can be doubled in 64 bit processors when compared with 32 bit processors. Some recent works on implementations of SHA-3 candidates using AVX instructions show very reasonable results [11]. Similarly, an operation which is well suited for SIMD parallelization can take advantage of multi-core processors as well. Therefore performance improvement studies of stream ciphers using AVX instructions and multi-core processors such as graphics processing units (GPU) will be an interesting extension to this work.