Extended forecast of economic results: instrumental potential of the fuzzy sets theory

The issues of assessing economic results are highlighted in the works of many economists and mathematicians. In order to ensure the commensurability of diverse costs, the principle of discounting was introduced, on the basis of which the most popular method of net present value has been developed, as well as other methods ideologically close to it. It is proposed to take into account an inherent uncertainty that arises while forecasting the flow of revenues and expenses in the implementation of projects through the following: the consolidated assessment of sustainability; the calculation of the break-even levels; the variations of the project’s parameters; the project’s evaluation considering the quantitative characteristics of uncertainty [1]. At that, it is recognized that these approaches are effective, when the project’s key parameters have no more than 15 – 20% of variations. And in the case of longterm estimates, for example, of the economic efficiency of the development of oil and gas resources, such key parameter, as their volume may differ manifold from the actual one. From the standpoint of the above-mentioned approaches, the task of evaluating such projects is unsolvable, and there is no methodological research on the forecast of economic efficiency of investments in long-term projects, which would take into account the inherently high uncertainty of their implementation conditions.

The fuzzy sets theory, developed since the 1960s, has been widely used in the spheres, where it isn’t expedient to apply the methods requiring a high accuracy of the source data due to the complexity of simulated processes and objects. This concerns natural, biological, and social systems in particular, in which the number of parameters and factors determining their development is so great, and the complexity of interaction is so diverse that any modeling accuracy is out of the question. The methods of the fuzzy sets theory are naturally applied in this sphere, and this has been going on for the last 10 – 30 years [7].

For estimating economic efficiency, a fuzzy sets method appears particularly suitable, which aggregates a variety of information in a uniform indicator under the conditions of low reliability of the source data [6]. The fact, that the use of generally accepted methods in such case can only give an approximate idea concerning the project’s economic parameters, also leads to the idea of the priority of methods that do not require time-consuming detailed forecasting of the streams of revenues and costs, but ultimately provide the similar generalized evaluation. The present work was aimed at identifying the opportunities for using the economic parameters assessment methods on the basis of the fuzziness principle.

Conventionally, the uncertainty in the conditions of functioning and development of economic agents is considered to be a source of risk and an obstacle to the adoption of sound managerial decisions (especially in the long-term perspective, when the uncertainty is high). And this is well-grounded. But as the uncertainty is fundamentally unavoidable, we can only try to reduce it, we have to develop methods of decision-making with an eye to this regular companion of any activities beyond the scope of immediate interest. And the question arises: if it is impossible to eliminate the negative effects of uncertainty, then can we find among its characteristics the aspects, the use of which would help in the planning of one’s activities? Such positive point may consist in the identifying the heterogeneity, the variability of the uncertainty and the use of such information for assessing the options for the operation or development of an object of research. It is clear that in this case we speak not about time heterogeneity, but, for example, space or element-by-element heterogeneity (in the framework of the system under consideration).

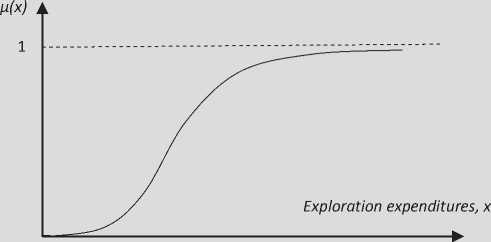
Such an opportunity is available in the business related to the search for and exploration of mineral resources, where the aspects of uncertainty, that have a spatial character, are of a significant and often crucial importance. If you learn to assess the uncertainty and find its spatial distribution, then it would be possible to structure the uncertainty. This will provide the basis for the differentiation of information concerning the structure of the subsurface and the presence of minerals by the levels of its reliability for different parts of an area, which directly determines the risk when choosing a solution. It is proposed to assess the accuracy of the information using membership functions μ(x) of the fuzzy sets theory [2]. When modeling the reliability, among the well-known models of membership functions, the function ц ( х ) = 1 - е ^{- кх} 2 , х >  0, к >  0 (fig. 1) (where the x-axis measures the expenditures on the exploration of the territory) most adequately describes the non-linear approximation of geological models of the structure of the earth entrails to the actual situation according to the expansion of its exploration. The problem of scaling the membership function is solved on the basis of the author’s modification of the analytic hierarchy process developed by T. Saaty [5].

Figure 1. Standard graph of the membership function for the modeling of reliability of geological constructions

The implementation of the proposed approach requires the skill of expressing numerically the uncertainty (or its opposite – validity) of the level of knowledge on the oil and gas bearing capacity of territories and the ability to register the spatial distribution of these resources. The next important step in making sound decisions concerning the choice of optimal directions of exploration work, capable of reducing the uncertainty to an acceptable level, will be the calculation of their cost estimates. Methods based on the fuzzy sets theory have been also developed for this purpose. The modeling of the certainty index is carried out by means of the membership function [2]. The most adequate to the task at hand was the S-shaped function, similar to the one above. Numerically, the uncertainty index was calculated in each elementary cell of the map in accordance with the 4-component model of the hydrocarbon deposit [3], when it is viewed as the result of the implementation of the following conditions:

• •    geometric (reflects the depth of layers in the subsoil and the possibility of existence of a trap);

• •    porosity and permeability (indicates the presence of container rocks and their permeability);

• •    presence of insulation (detects the presence of impermeable layers, keeping the oil and gas fluid in the trap);

• •    presence of the fluid in the depths.

In the cells, where the wells have been drilled, the value of the membership function is the maximum, and in the rest of the cells it decreases in accordance with the function of accounting the informational impact, that is as follows: f ( х ) = - (fig. 2) , where the

1 + k • x ²

parameter k (1 ≤ k ≤ 3) determines the speed of decreasing informational influence, depending on the distance x .

The obtained maps of the validity index distribution (fig. 3) can essentially serve as a working tool for selecting the exploration direction and decision-making by, for instance, comparing “white” and “light gray” areas on the validity map with the forecasts of their exploitability.

The evaluation of the amount of funding required for the additional exploration of the territory or its part, possessing the major exploratory interest, up to the level enabling the sound decision-making will contribute to a more balanced approach to the planning of geological exploration activities. The numerical value of this validity level is determined in accordance with the membership function (see fig. 1). It can be seen that in the area of an inflection point, the ordinate of which is equal to 1 - e ^{- 0,}5 = 0.4, with the increase in the volume of exploration works, the validity is increasing most rapidly, and then it abruptly slows down.

Figure 2. The function of accounting the informational impact

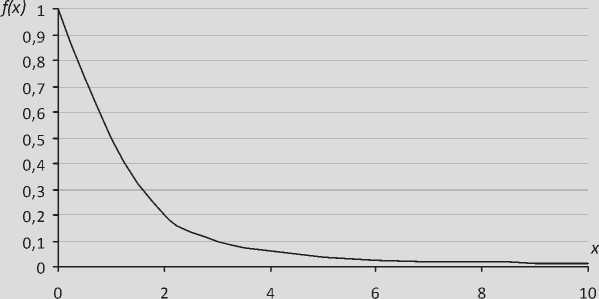
Figure 3. Schematic map of the validity index for the search of hydrocarbon deposits (the case of the Timan-Pechora oil-and-gas province) [4]

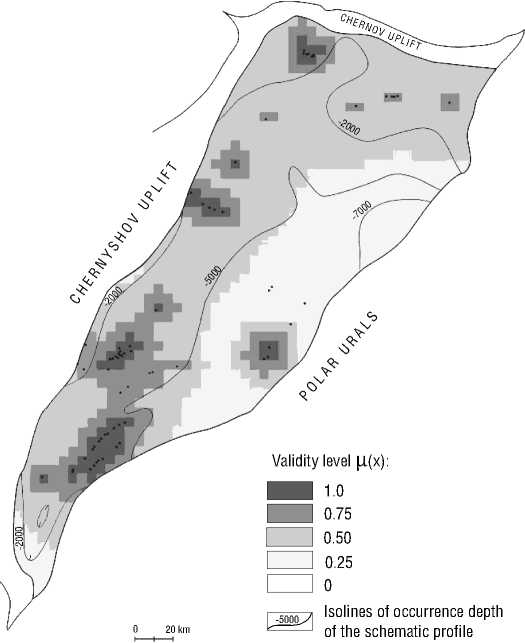
of the surface, m

Therefore, from a practical point of view, it is expedient to limit the validity value at 0.7 and consider it the threshold of information sufficiency (for complex areas its value may be increased, but not more than 0.8) [4].

The validity of the models of constructing and evaluating the prospects for oil and gas content of the territory under exploration is calculated for each elementary cell of the territory – the arithmetic average of the

Hamming distances for each component of the model of the oil-gas field is calculated:

d (A, B) = ¹ ₄-SI μ_A (x_i ) – μ_B (x_i ) , ⁴ i = 1

where μA and μB are the values of the membership function, corresponding to the appropriate level of information adequacy and the current state of exploration, i is the number of the component of the above model of the oil-gas field.

The map in fig. 3 has been created on the basis of such calculations. The transition to the value indicator of the amount of works for a detailed exploration of the territory (with the unit cost indicators for its imple- mentation being 300 rubles/ ton of fuel oil equivalent) gives a value between 1.2 + 0.2 billion rubles.

Thus, with respect to the exploration of oil and gas, it became possible to change the uncertainty from the factor that impedes the adoption of sound managerial decisions into an instrument of making such decisions. And this approach will be useful in many industries, where there is a possibility to select the factors, crucially influencing the economic performance of a studied object or system, and to simulate the level of validity of the current knowledge concerning these factors, as well as the influence of the factors on the results by means of the fuzzy sets theory.