Face recognition based on cross diagonal complete motif matrix

Published Online March 2018 in MECS

Since last century many researchers worked and derived many models or methods for automatic face recognition [1], [2]. It has great potential in various applications, like, photo album management in social networks, human machine interaction, and digital entertainment, etc. Face recognition method, tries to find act the matching face, for the given test or input face of a person, from the database. Building an automatic Face Recognition that matches with the human eye is a challenging task. These challenges are mainly because of large or moderate variations of human faces due to illumination, expression, pose, corruption, and occlusion [3], [4]. Due to these reasons, face recognition can be categorized as a special subset of object recognition. However, face recognition has to tolerate more difficulties in identifying or defining small, distinct and significant features from each face of a person (intra-object categorization) contrary to usual object recognition (inter-object categorization). Therefore one needs to identify a good, precise and accurate feature extraction strategy for efficient face recognition.

The feature extraction methods of Face Recognition are mainly divided into two categories: i) Holistic feature based [5]–[7] ii) Local feature based [8]. The popular methods of Face Recognition like Independent Component Analysis [6], Linear Discriminant Analysis (LDA) [7] and Principal Component Analysis (PCA) [5] are the best examples for holistic approaches. Recently, local feature based methods have become more popular and significant than holistic methods because the local features are more stable to local variations, such as illumination, expression, and occlusions [9],[10]. The Gabor wavelet [11], [12] is a successful local descriptor because of its biological relevance and computational properties [11]. The most popular feature extraction techniques used in face recognition are: the scale invariant feature transform (SIFT) [13], the histogram of oriented gradients (HOG) [14], the local binary pattern (LBP) [15]. LBP identifies the spatial relationships amongst the pixels in the local neighborhood of the facial images in an efficient manner. The LBP methods proved to be highly robust to even nonlinear illumination variations. Further the local face recognition methods are more preferable than global feature extraction methods because one can derive more meaningful information of the face. The familiar and popular ones in this model are: contour curve and angular points [16] model, Hidden Markov Model [17], linear discrimination analysis [18], local binary model [19], deep hidden identity feature [20]. The local phase quantization (LPQ) [21], and the binarized statistical image features (BSIF) [22] are also popular local models. The main disadvantage of deep learning methods is they always require a very huge amount of training data and computation cost.

This paper is motivated by the static motifs [23], where the initial peano scan position (PSP) is fixed on a 2 x 2 grid, the LBP model (3 x 3 neighborhood) and GLCM features. This paper with the above motivations derived a cross and diagonal complete motif matrices by dividing the 3 x 3 neighborhood into dual 2 x 2 neighborhoods. The initial Peano Scan Position (PSP) of complete motif begins with the least pixel intensity value position of the 2 x 2 grid.

This paper is organized as follows; the section two gives the related work, section three gives the derivation of proposed method followed by results and discussions in section four. The conclusions are given in section five.

• II.    Related Work

Various approaches based on space filling curves were studied [24, 25] in the literature for various applications like CBIR [24, 25], data compression [26], texture analysis [27, 28] and computer graphics[29]. Space curves are basically straight lines that pass through each and every point, of bounded sub space or grid, exactly once in a connected manner. The Peano scans are basically space filling curves or connected points , spanned over a boundary and known as space filling curves. The connected points may belong to two or higher dimensions. The Peano scans are more useful in pipelined computations where scalability is the main performance objective [30-32]. The Peano Scans also provide an outline for handling larger dimensional data, which is not easily possible by the use of conventional methods [33].

To capture the low level semantics of space filling curves on a 2 x 2 grid a set of six Peano scan motifs (PSM) are proposed in the literature recently [23]. The Peano scan motif’s moves around the 2x2 grid, by visiting each pixel location exactly once. The path or shape of the motif is guided by the incremental pixel intensity values of the 2x2 grid. The six motifs derived by Jhanvir et al. [23] are shown in Fig.1 and they are initiated from top left most corner of the 2x2 grid. Each of these six different motifs represents a distinctive shape of pixels on the 2 x 2 grid (starting from top left corner) as shown in Fig.1. A compound string may result from all six motifs, if one traverses the 2 x 2 neighborhood based on a contrast value. Based on the texture contrast features over 2 x 2, grid a particular motif out of the above six motifs will be resulted. Each motif on the 2 x 2 grid is represented with an index value ranging from 0 to 5. This transforms the input image into a motif image with six index values. A cooccurrence matrix on this motif index image is derived and named as Motif co-occurrence matrix (MCM) and used for CBIR [23].

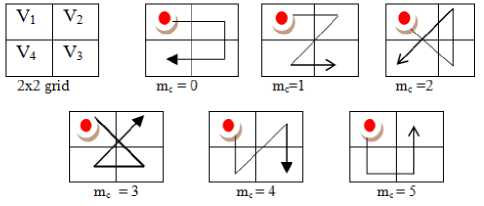
Fig. 1. A 2x2 grid and six Peano motifs.

• III.    Proposed Method

• A.    Derivation of complete motif matrix (CMM) image

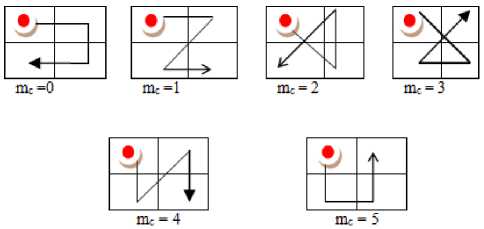
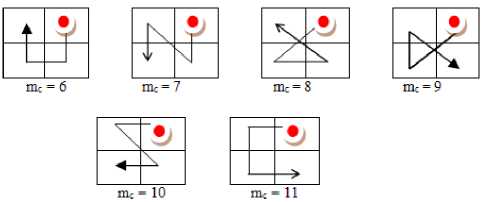
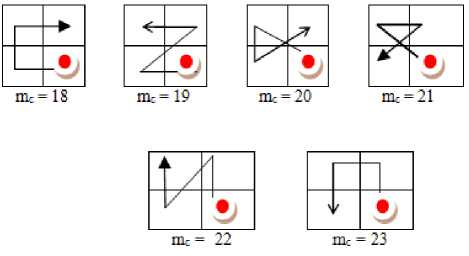
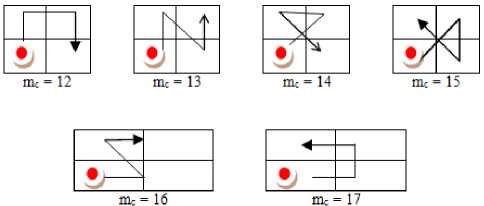
Jhanvar et al. [23] derived Motif matrix (MM) on a 2 x 2 grid by fixing the initial Peano scan position (PSP) and then derived co-occurrence matrix on MM. This approach has several disadvantages: i) basically it is static , as it always assumes the least pixel value of a 2 x 2 grid is at top left most position. ii) it does not represent complete Peano Scan information and hence fails in representing complete shape information. To overcome this issue , in this paper initially derived Complete Peano Scan (CPS) or Complete Motif Matrix (CMM) on the 2 x 2 grid by not fixing the initial PSP i.e. in CMM approach , the initial PSP starts from a pixel position whose pixel intensity value is least. Thus the proposed CMM method is completely dynamic. On a 2 x 2 grid the initial PSP can be at one of the following four positions: i) top most left; ii) top most right; iii) bottom most left ; iv) bottom most right. This CMM approach can generate twenty four different complete motifs, each representing a particular shape , if one does not fix the initial point i.e. the initial point of the motif starts from a pixel position whose pixel intensity value is least. The complete motif matrix (CMM) code M c ranges from 0 to 23. Fig.2 displays the 24 different motifs that can be derived from a 2x2 grid. The motifs M c ranging from 0 to 5, 6 to 11, 12 to 17 and 18 to 23 are derived based on incremental pixel intensities by assuming the least pixel intensity value is at top left most corner, top right most corner, bottom left most corner and bottom right most corner of 2x2 grid respectively as shown in Fig.2 2(a), 2(b), 2(c) and 2(d) respectively.

(a)

(b)

the second set consists of diagonal pixels (Fig 3). The values of cross and diagonal pixel intensities are computed by considering the absolute difference between central pixel and neighboring pixels of 3 x 3 neighborhood as given in equation 1 (Fig . 3) .

C i =| E c – E i | where i=2|4|6|8             (1)

D i =| E c – E i | where i=1|3|5|7

(d)

Fig.2. The complete motifs on a 2x2 grid: 2(a) PSP initiated from top left most corner 2(b) PSP initiated from top right most corner 2(c) PSP initiated from bottom leftmost corner (d) initiated from bottom right most corner.

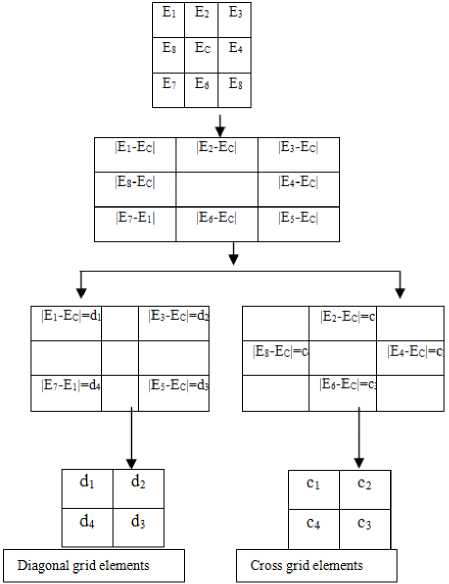
Fig.3. Formation of cross and diagonal 2 x 2 grids from 3 x 3 neighborhoods.

(c)

• B.    Derivation of cross diagonal complete motif cooccurrence matrix (CD-CMM) on 3 x 3 neighborhood

Most of the ‘local feature’ models in the literature, extracted the neighboring pixel information around the central pixel to obtain an efficient Face Recognition model. The GLCM method characterizes the spatial relationship between a pixel and a neighboring pixel based on a given specific distance and angle. For the same distance‘d’ the GLCM method can extract spatial relationship between pixel with different angles. The motif based methods are popular in the literature for texture classification, analysis and retrieval. The earlier methods derived the partial or static motifs on a 2x2 grid and this paper extended the concept by deriving complete or dynamic motifs on 3x3 grids. The 3 x 3 neighborhood approaches identify the spatial relationships among the pixels of the local neighborhood more precisely than 2x 2 grid approaches. The LBP based methods, derive texture information based on the neighboring pixels around the center pixel mostly on a 3 x 3 neighborhood. A 3 x 3 neighborhood will have 8-neighboring pixels {E1,E2 ….E8} around the central pixel Ec (Fig.3). This paper divided the 3 x 3 neighborhood into two sets, each with four pixels or 2 x 2 grids as shown in Fig. 3. The first set consists of cross pixel elements and

This paper derived CMM on cross and diagonal grids of 3 x 3 neighborhood. The present paper derived local texture information from the mathematical model representing the two groups of 3 x 3 neighborhood i.e., Cross Complete motif matrix (CCMM) and Diagonal complete motif matrix (DCMM).The elements of CCMM and DCMM are located in the cross and diagonal directions with respect to the reference of central pixel of the 3 x 3 neighborhood. The CCMM and DCMM are represented by one of the possible complete motif index values from 0 to 23 and each pattern represents a particular shape of PSP. The advantage of CMM is, its index does not depend on the order of PSP. An example of transforming an image neighborhood into CCMM and DCMM is shown in Fig 4. Based on the index values of CCMM and DCMM, this paper derived “cross diagonal complete motif co-occurrence matrix (CD-CMM)”.The CD-CMM measures the relative frequencies of CCMM and DCMM i.e., the index values of CCMM on x-axis and DCMM on Y-axis. This paper derived a set of Haralick features on CD-CMM to obtain more precise and prominent local texture information from facial images. This new matrix i.e.,CD-CMM combines the merits of both complete motifs matrix, LBP and GLCM methods of texture analysis and hence it gives more complete texture information about the facial image. The dimension of the CD-CMM is 24*24. Further, the grey level of the image has no effect on the dimension of the CD-CMM, so that it reduces the dimensionality problem and hence time complexity or computational time is reduced considerably. The process of transformation of a 3 x 3 neighborhood in to CDCMM is Fig. 4 Example of transforming a 3 X 3 neighborhood into CD-CMM.

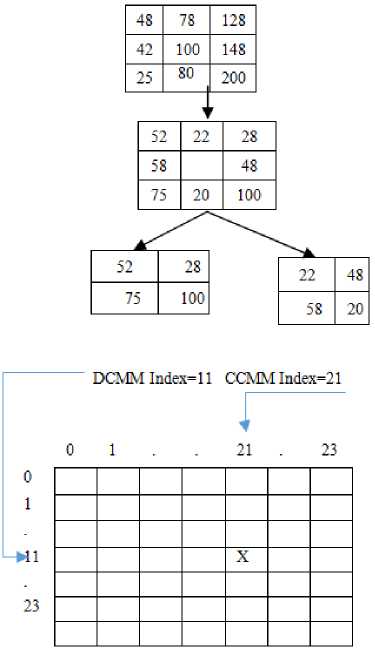
Fig.4. Example of transforming a 3 X 3 neighborhood into CD-CMM.

• IV. Results and Discussions

To test the efficacy of the proposed method, this paper selected the popular facial data bases that are used for face recognition in the literature i.e., ORL data set, Yale B Face Database, FERET and CMU Multi-PIE. The performance of the proposed CD-CMM descriptor is computed on these facial data bases and compared with seven state-of-the-art face image descriptors, i.e., MCM[23], LBP [19], LTP [34], LPQ [21], multi-scale LBP (MsLBP) [35], Multi-scale DLBP (MsDLBP) [36]. The above existing descriptors are based on local features. This paper used Chi-square distance metric as given in equation 2.

R(d,t)=min B (^ (i=1)^An^(( K d i-t i) 3 ^A2/(d i+t i))/2)

Where d, t are two image features and R(d,t) is the histogram distance for recognition.

A brief description about these databases is given below.

• A.    The ORL Face Data Set

The ORL data set [37] contains images from 40 subjects and each subject contains ten face images. This results a total of 400 (40 x 10) face images in ORL data base. For most of the subjects, the images are captured at different times with varying facial details i.e., with glasses and without glasses; with varying lighting conditions; with varying facial expressions like open/closed eyes, smiling/not smiling, etc. The first 2-6 face images of each subject were used as training samples and the remaining face images were used as test samples. Fig. 5 shows some face images from this data set. The experimental results are presented in Table I.

Fig.5. Sample facial images of ORL database.

• B.    The Extended Yale B Face Data Set

  The Extended Yale B [38] face data set contains frontal facial images of 38 individuals and more than sixty facial images per each individual and a total of 2414 facial images. Images are captured under varying lightening conditions. The 20 facial images were selected randomly of each individual for training purpose and the remaining face images were viewed as testing samples. Fig. 6 shows some face images from the Extended Yale B face data set. The experimental results are presented in Table I

Table I. Classification accuracies of different methods on the ORL Face Data set.

Table II. Classification accuracies of different methods on the Yale Data set.

Number of training samples per subject	2	3	4	5	6	Avg:
Proposed CD-	90.87	91.44	95.78	95.63	97.12	94.17
LBP	84.26	86.35	91.20	91.56	93.25	89.32
LTP	85.63	88.47	92.01	92.11	94.75	90.59
LPQ	89.67	90.35	95.64	94.26	96.75	93.33
MsLBP	86.45	90.25	93.21	93.14	95.62	91.73
MsDLBP	83.12	85.14	89.47	90.45	92.14	88.06
MCM[23]	85.95	87.91	84.75	83.87	83.89	85.27

Number of training samples per subject	8	10	12	14	16	18	Avg:
Proposed CDCMM	81.63	84.63	86.67	89.56	89.98	90.32	87.13
LBP	77.41	78.48	79.89	81.54	84.68	85.64	81.27
LTP	79.84	81.46	82.47	84.57	86.48	87.65	83.75
LPQ	76.15	80.41	84.56	88.32	89.11	89.63	84.70
MsLBP	80.11	82.78	83.66	85.14	86.52	88.52	84.46
MsDLBP	74.69	74.85	76.35	78.56	82.56	84.62	78.61
MCM[23]	72.91	73.79	78.89	76.99	80.99	80.10	77.27

Y2_F1

Y2_F2              Y2_F3

Y2_F4

Y2_F5              Y2_F6

Y3_F1

Y3_F2

Y3_F3              Y3_F4              Y3_F5              Y3_F6

Fig.6. Sample facial images of Yale database

• C.    The FERET Face Data Set

  This paper used a subset of FERET face data set [39] that contains facial images of 200 people or subjects with 7 images per person. This leads to a total of 1400 face images.

The first 2–5 face images of each person were used as training set and the remaining face images were used as probe or test samples. Fig. 7 shows some of these face images.

Fig.7. Sample facial images of FERET database.

Table III. Classification accuracies of different methods on the FERET Face Data set.

Number of training samples per subject	2	3	4	5	Avg:
Proposed CD-CMM	75.61	70.23	84.25	91.32	80.35
LBP	64.63	59.15	79.68	88.26	72.93
LTP	72.65	68.52	81.25	89.42	77.96
LPQ	73.15	69.86	82.69	90.15	78.96
MsLBP	73.10	69.72	82.21	89.96	78.75
MsDLBP	63.67	58.25	77.97	82.68	70.64
MCM[23]	66.98	69.86	74.89	71.12	70.77

D. The CMU Multi-PIE Face Data Set

Fig.8. The sample facial images from CMU-PIE database.

The CMU Multi-PIE face data set is composed of a face image of 337 persons. These images are captured with variations of poses, expressions, and illuminations. In this paper, we have selected a subset of 249 persons face images under 7 different illumination conditions with a smile expression and with a frontal pose under 20 different illumination conditions. For training purpose , this paper selected only one face image from 7 smiling images and face images corresponding to the first 3, 5, 7, 9 illuminations from the 20 illuminations. The remaining face images of this data base were used for probe sets. Fig. 8 shows some face images from this data set. Table IV displayed the experimental results on this database.

From the experimental results the following are noted.

• 1.    The MCM descriptor exhibited a mean recognition rate of 85.27 percent and other LBP based descriptors shown an improvement than MCM by 4 to 8 percent on ORL face dataset. However the proposed CD-CMM has shown almost a high mean recognition rate by 9 percent when compared to MCM and a high mean recognition rate by 1 to 8% when compared to other LBP based

• 2.    The proposed CD-CMM descriptor exhibited a 10% high performance when compared to its counterpart MCM on Yale B Face Data set. Our method shown with superior mean recognition rate by as much as 3 to 6 percent when compared to other variants of LBP based descriptors.

• 3.    Good performance is achieved by all descriptors on FERET database; however, the proposed CDCMM achieved with superior mean recognition rate by as much as 2 to 10 percent than other descriptors.

• 4.    The existing methods and proposed method shown a high Face Recognition rate of above 90% on CMU-Multi-PIE face database.

• 5.    Out of the five LBP based descriptors, the LPQ followed by MsLBP and LTP achieved a good recognition rate with a mean variation of 2 to 4 percent on all face data sets.

• 6.    The Face Recognition rate, for all descriptors and on all databases, shows an increasing trend as the number of training samples per subject increases.

descriptors on ORL face dataset. The LPQ and our method exhibited almost similar classification rates.

Table 1V. Classification accuracies of different methods on the CMU Multi-PIE Face Data set

Number of training samples per subject	4	6	8	10	Avg:
Proposed CD-CMM	98.23	98.63	99.11	99.72	98.92
LBP	90.11	92.45	94.32	95.61	93.12
LTP	92.10	94.52	96.33	97.23	95.05
LPQ	96.68	98.65	99.12	99.46	98.48
MsLBP	94.32	96.32	98.65	99.12	97.10
MsDLBP	91.32	92.68	95.36	96.10	93.87
MCM[23]	92.32	94.96	96.86	97.88	95.51

Our proposed CD-CMM obtains better face recognition rate than other LBP based methods and MCM approach. It indicates that our method is more robust to various variations (illuminations, facial expressions, and poses) of human face images. The existing LBP and its variants i.e., LBP, LTP, LPQ, MsLBP, MsDLBP, the motif based approach MCM and the proposed CD-CMM exhibited high performance on relatively small-scale data sets (e.g., the ORL data set) and the data sets with slight pose or expression variations (e.g., the CMU-Multi-PIE data set).

The excellent performance of CD-CMM explained as follows. The Complete motif matrix is capable to encode more discriminative texture information. The novelty of this paper is the derivation of complete motif matrix on a 3x 3 neighborhood by partitioning it in to cross and diagonal grids, which has provided the significant local information more precisely than MCM. The second-order statistics in the form of GLCM features on CD-CMM encoded most informative directions on human face; and the dual-cross and diagonal grouping strategy ensures good complementarity between the two encoders.

The main contributions of this paper are given below:

• 1.    The existing MCM [22] is derived on the 2 x 2 grid by fixing the initial position of the PSM, however the proposed CD-CMM is derived on the 3 x 3 neighborhood by dividing it in to two separate 2 x 2 grids and the initial position of the PSM is not fixed. Therefore the proposed CD-CMM derives complete motif information instead of partial information in the case of MCM.

• 2.    The existing methods derives PSMs on the 2 x 2 grid and transforms the grey level image in to motif indexed image with index value ranging from 0 to 5; However the proposed CD-CMM derives complete motif indexes on a 3 x 3 neighborhood with index values ranging from 0 to 23, and thus provides more significant and precise information.

• V. Conclusion

The proposed CD-CMM method derived a strong facial representation and it is more efficient in representing the facial image features than the other methods because this paper integrated i) local neighborhood strategy, ii) cross and diagonal complete texton matrices iii) GLCM features. The local neighborhood strategy i.e., the absolute difference of grey levels between neighboring and central pixel, captured the local information around the central pixel more precisely. The complete motifs on the 3 x 3 neighborhood are computed by dividing it into cross and diagonal matrices of 2 x 2 grids. This derivation of GLCM on cross diagonal complete motifs has established the strong relationship between the cross and diagonal motifs and derived CD-CMM. The choice of a particular motif over a 2 x 2 grid depends upon the local texture occupying the grid. The statistical features on CD-CMM provided the rich description of the low level semantics of the facial image. The CD-CMM approach is different from many other intensity based methods as well as gradient magnitudes and gradient orientations based ones. The CD-CMM descriptor also enriches discrimination power with meaningful visual features i.e. local contrast, edges, borders, shapes based on intensity differences, discontinuities properties etc., thus making CD-CMM more robust against face recognition challenges such as illumination, pose and time-lapse variations.