Face Recognition Based on Principal Component Analysis

Face Recognition area is one hot research area in the field of computer vision. There has been plenty of work done in face recognition some of the work has been mentioned here for reference [1, 2, 3, 4, 5]. Face Recognition has been used in various applications where personal identification is required for example in Visual Attendance system where student identification and recognition is achieved through face recognition, in gaming applications, in security applications, in short face recognition applications are used in widely in many corporate and educational institutions. Many techniques can be used for face recognition but Principle Component Analysis is mostly followed and good technique. Principal component analysis (PCA) involves a mathematical procedure that transforms a number of possibly correlated variables into a smaller number of uncorrelated variables called principal components. The first principal component accounts for as much of the variability in the data as possible, and each succeeding component accounts for as much of the remaining variability as possible. Now it is mostly used as a tool in exploratory data analysis and for making predictive models. PCA involves the calculation of the eigenvalue decomposition of a data covariance matrix or singular value decomposition of a data matrix, usually after mean centering the data for each attribute. Some of the work regarding eigen faces has been mentioned for literature [3, 6]. The results of a PCA are usually discussed in terms of component scores and loadings. PCA is theoretically the optimal linear scheme, in terms of least mean square error, for compressing a set of high dimensional vectors into a set of lower dimensional vectors and then reconstructing the original set. It is a non-parametric analysis and the answer is unique and independent of any hypothesis about data probability distribution. However, the PCA compressions often incur loss of information.

The paper is organized as follows: In section II, previously developed systems related to this work have been discussed. Section III presents the proposed system architecture. In section IV the proposed methodology of the system has been discussed. In section V experimental setup and results has been presented. Section VI depicts the conclusion and future work.

• II.    LITERATURE REVIEW

Human often use faces to recognize individuals and the advancement in computing capability over the past few decades now enable similar recognition automatically. Early face recognition algorithms use simple geometric models, but the recognition process has now matured into a science of sophisticated mathematical representations and matching processes. The proposed system for face recognition required the administrator to locate features (such as eyes, ears, nose, and mouth) on the photographs before it calculated distances and ratios to a common reference point, which were then compared to reference data. Goldstein, Harmon, and Lesk [7] used 21 specific subjective markers such as hair color and lip thickness to automate the recognition. The problem with both of these early solutions was the manual computation of the measurements and locations. Kirby and Sirovich[8] applied principle component analysis, a standard linear algebra technique, to the face recognition problem. This was considered somewhat of a milestone as it showed that less than one hundred values were required to accurately code a suitably aligned and normalized image. Turk and Pentland[9] discovered that while using the Eigen faces techniques, the residual error could be used to detect faces in images, a discovery that enabled reliable real-time automated face recognition systems. Although the approach was somewhat constrained by environmental factors, it nonetheless created significant interest in furthering development of automated face recognition technologies. Kwang In Kim, Keechul Jung, and Hang Joon Kim [10] proposed a kernel principal component analysis (PCA) as a nonlinear extension of a PCA. The basic idea of kernel PCA is to first map the input data into a feature space via a nonlinear mapping and then principal components has been computed in that feature space. This letter adopts the kernel PCA as a mechanism for extracting facial features. Through adopting a polynomial kernel, the principal components can be computed within the space spanned by high order correlations of input pixels making up a facial image thereby producing a good performance. Xin, Patrick, Kevin [11] uses the PCA algorithm to study the comparison and combination of infrared and typical visible-light images for face recognition. This study examines the effects of lighting change, facial expression change and passage of time between the gallery image and probe image. Experimental results indicate that when there is substantial passage of time (greater than one week) between the gallery and probe images, recognition from typical visible-light images may outperform that from infrared images. Experimental results also indicate that the combination of the two generally out-performs either one alone. Neerja and Ekta Walia[12] proposed a system in which the database is sub grouped using some features of interest in faces. Only one of the obtained subgroups is provided to PCA for recognition. The performance of the proposed algorithm is tested on our university database of faces.

• III.    SYSTEM ARCHITECTURE

The proposed system captures the images of the same object from different angles by using static digital camera. The alignment of the object is performed in the preprocessing phase. Noise removal has also been achieved in the preprocessing phase by applying Gaussian filter. The cropping of the face portion from the image has been done after capturing the image.

Face detection has been applied on the images after preprocessing. Face detection is a starting point for face recognition. The system performs the face detection of all images taken by the digital camera. In database phase, the proposed system creates a database and stores all the preprocessed images in this database and finally system creates a database matrix and the system perform all the operations on the database matrix. The Principle Component Analysis technique has been applied on the images of the database system. The proposed system uses the test images stored in the database. The system implement Principal Component Analysis algorithm on the test images. Now system compares the capture images taken by digital camera and test images one by one. Finally the system provides the results which show the name of the person and face marked by the bounding box. The system flow chart is shown in Fig.1.

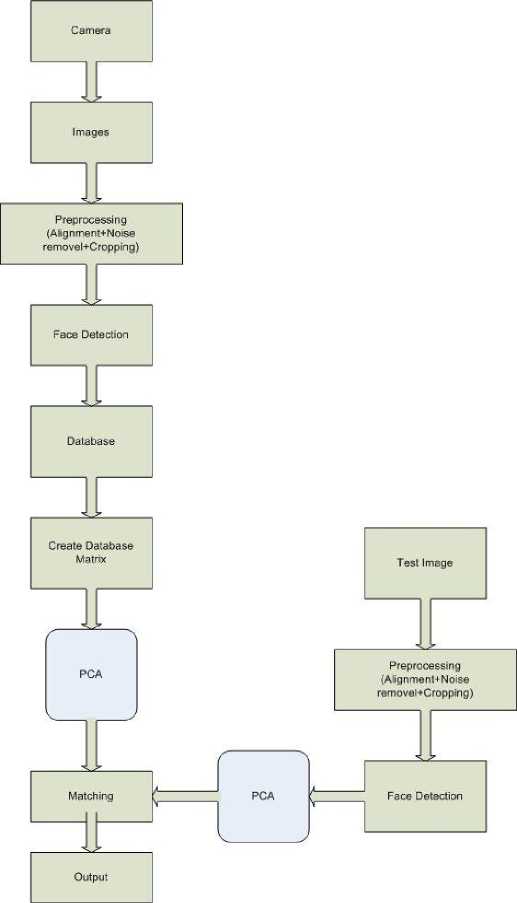
Figure 1: System Architecture

• IV.    PROPOSED METHODOLOGY

Face detection can be regarded as a specific case of object-class detection. In object-class detection, the task is to find the locations and sizes of all objects in an image that belong to a given class. Examples include upper torsos, pedestrians, and cars. Face detection can be regarded as a more general case of face localization. In face localization, the task is to find the locations and sizes of a known number of faces (usually one). The proposed system implements the face-detection task as a binary pattern-classification task. The image is transformed into features and the trained classifier decides whether that particular region of the image represents the face or not. The proposed system employs a window-sliding technique. That is, the classifier is used to classify the (usually square or rectangular) portions of an image, at all locations and scales, as either faces or non-faces (background pattern).PCA is mathematically defined as an orthogonal linear transformation that transforms the data to a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so on. PCA is theoretically the optimum transform for given data in least square terms. For a data matrix, XT, with zero empirical mean (the empirical mean of the distribution has been subtracted from the data set), where each row represents a different repetition of the experiment, and each column gives the results from a particular probe. In the proposed system given a set of points in Euclidean space, the first principal component (the eigenvector with the largest eigenvalue) corresponds to a line that passes through the mean and minimizes sum squared error with those points. The second principal component corresponds to the same concept after all correlation with the first principal component has been subtracted out from the points. Each eigenvalue indicates the portion of the variance that is correlated with each eigenvector. Thus, the sum of all the eigenvalues is equal to the sum squared distance of the points with their mean divided by the number of dimensions. PCA essentially rotates the set of points around their mean in order to align with the first few principal components. This moves as much of the variance as possible (using a linear transformation) into the first few dimensions. The values in the remaining dimensions, therefore, tend to be highly correlated and may be dropped with minimal loss of information. PCA is often used in this manner for dimensionality reduction. The proposed system has the distinction of being the optimal linear transformation for keeping the subspace that has largest variance. This advantage, however, comes at the price of greater computational requirement if compared, for example, to the discrete cosine transform.   Nonlinear dimensionality reduction techniques tend to be more computationally demanding than PCA.

• A.    Image acquisition

The first step in proposed system is to acquire the images of the persons from different angles by the use of static digital camera.

• B.    Image preprocessing

The face images of the persons have been aligned in the preprocessing phase. The next process in the preprocessing phase involves the operation of cropping on the images.

• C.    Face detection

The proposed model can contain the appearance, shape, and motion of faces. There are several shapes of faces. Some common ones are oval, rectangle, round, square, heart, and triangle. In the proposed system, motions include, but not limited to, blinking, raised eyebrows, flared nostrils, wrinkled forehead, and opened mouth. The face models will not be able to represent any person making any expression, but the technique does result in an acceptable degree of accuracy. The models are passed over the image to find faces, however this technique works better with face tracking. Once the face is detected, the model is laid over the face and the system is able to track face movements.

• D.    Create a database

First there is a need to create an image database of different people. It has been considered that there can be a change in the expression of the people so database has been created with 2 or 3 different expressions for better results. The environment will be controlled and the background and light will be uniform so this will handle the illumination problem. In the proposed system frontal as well as side poses have been considered.

• E.    Reshaping the images

The shape of each image has been changed in order to create a data matrix of all the images. A m x n matrix has been converted into m*n x 1 matrix having number of rows equal to the product of number of rows and columns of the original matrix, and a single column

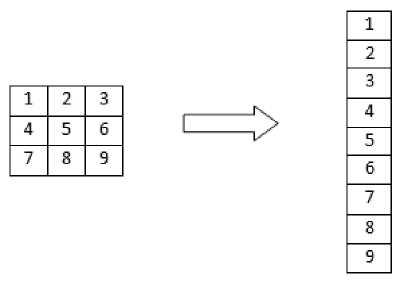
Figure 2: Reshaping image

• F.    Create the data matrix

The system will insert all the reshaped images into a new matrix (data matrix) as columns. For example in this case N images of m x n dimension the data matrix will have N columns and m*n rows.

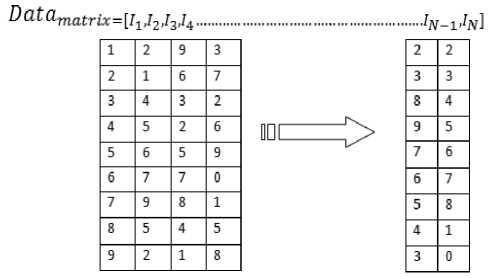
Figure 3: Arranging Reshaped images in the data matrix

• G.    Creating a mean matrix

The proposed system creates a mean matrix of all the different image matrices. The dimension of mean matrix will be the same as that of a single image matrix. The mean matrix will be calculated by adding all the columns of data matrix divided by the total number of columns i.e. N in this case is mean ^Z^14                       (1)

• H.    Subtract the mean from each column

The algorithm then subtracts the mean image from all the image matrices to get the mean subtracted data matrix.

A = [(^ - mean), (I₂ - m ean), . (I_w - me an)]     (2)

• I.    Create the covariance matrix

The system will make the covariance matrix by multiplying the mean subtracted matrix by its transpose to make it a square matrix in the next phase

C = A A^T                                     (3)

As Dim (A) = (m*n) x N and Dim (AT) = N x (m*n) SO Dim(C) = (m*n) x (m*n) which is very large and computation will be difficult. So another matrix has been created by rearranging

L = A^T A                                      (4)

Dim (L) = N x N which is easy to handle

• J.    Find the eigen values and vectors

Then the system finds the Eigen vectors and Eigen values. For N dimensional vector there will be N Eigen values and Eigen vectors.

• K.    Create an eigen image

The proposed system then creates an Eigen image by multiplying mean subtracted data matrix with the Eigen vectors.

EigIm ад e = (Л)^ ig V e c)                       (5)

• L.    Choosing highest eigen vectors

The proposed system then choose the highest eigen vectors by looking for highest eigen values let say 50% and then picking up the corresponding columns of the eigen image as they have the highest eigen vectors. Eigen vectors with the highest eigen values are the principle components of the data set having maximum information. This will also reduce the size of final data set.

• M.    Creating the weight matrix

The main data set known as the weight matrix has been created which is used for the identification process. This weight matrix has been calculated by multiplying the transposed large eigen image with the mean subtracted data matrix.

We ightMa ^=(lrg eig image^T)(A)              (6)

After this step the system can recognize any face image by comparing it with the main weight matrix.

• N.    Test image

On the other side a test image will be taken for comparison. Now preprocessing will be implemented on the test images similar to the preprocessing which is implemented on the real time image taken from camera

• O.    PCA algorithm on test images

The proposed system implements the Principle Component Analysis algorithm on the test images.

• P.    Matching

Now the real time image and the test image will be matched after the implementation of Principle Component Analysis algorithm.

• Q.    Output

Finally output images will be taken which will show the difference between the two images

• V.    EXPERIMENTAL SETUP AND RESULTS

• A.    Application Interface

The proposed system is designed to operate with a single static camera which is fixed at a particular location. Sony 8.1MP static camera is used for image acquisition which captures images at a spatial resolution of 640 x 480 pixels having a frame rate of 25 frames per second. A low cost camera is used for capturing images because one of the objectives of this research work was to design an economical system. The distance between the camera and the persons is roughly 7 to 8 meters.

• B.    Results

The performance of the proposed Face Recognition System is tested on different images in different poses recorded in different conditions. Some of the images include one person, some includes two persons and some includes more than that. In case of huge crowd encapsulating in image, the rate for correct recognition is little low as compared to the images with fewer persons where the false recognition rate goes pretty below around 1 to 2% resulting the correct recognition in the range of around 98 to 99% which shows excellent results.

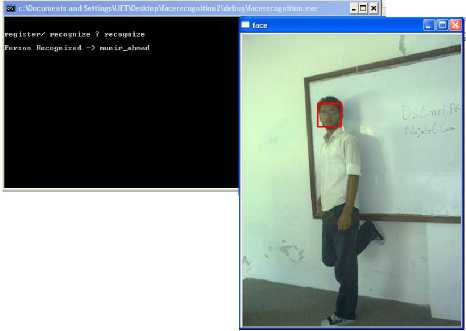
Figure 4: Angled Face view with one person in the scene

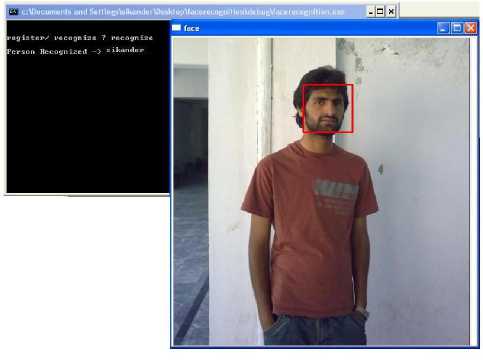
Figure 5: Frontal Face view with one person in the scene

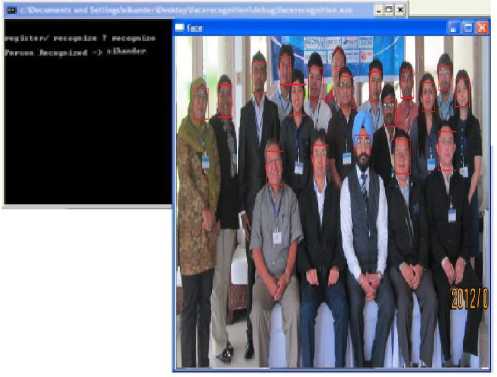
Figure 8: Frontal Face view with big audience in the scene

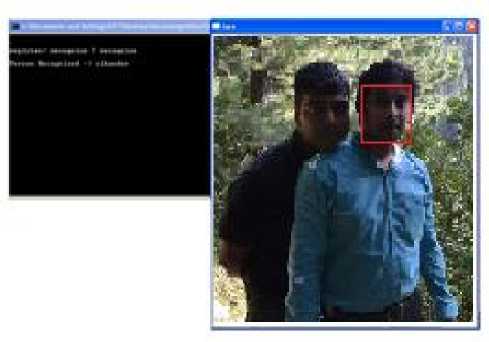
Figure 6: Frontal Face view with two persons in the scene

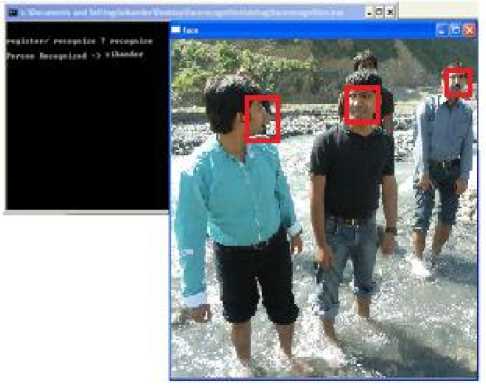
Figure 9: Frontal and Angled Face views in the scene

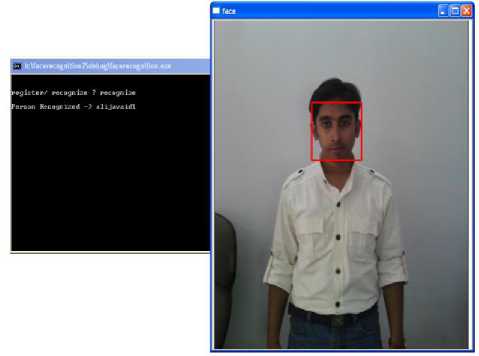
Figure 7: Frontal Face view with one person in the scene

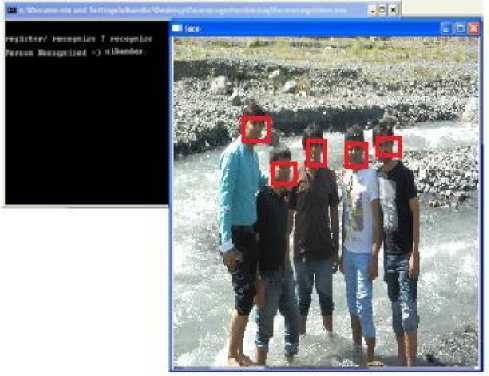
Figure 10: Frontal and Angled Face views in the scene

Fig. 11 presents some of the results of recognized faces from the experiments performed on proposed algorithm. The proposed algorithm performs very well especially in scenes of fewer persons and frontal views but also gives acceptable results for faces at different angles and with huge audience in the scene.

Figure 11: Recognized Faces

The experimental results of the proposed system are shown in fig. 12 and fig. 13. In fig. 12, the results show the correct and false recognition ratios for the four cases. Case 1 considers the scene where more than 10 persons exists in the captured image, Case 2 shows the case of around 10 persons, Case 3 is for 2 persons and last case shows the results of 1 person in the captured image. The Correct Recognition rate for Case 1 is around 80%, its 87% for Case 2, 93% for Case 3 and 99% for Case 4.

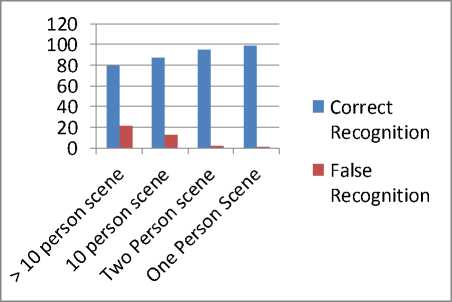
Figure 12: Recognition Results with varying audience in the scene

Fig. 12 shows the experimental results in case of different face angles of persons in the scene, obviously the audience in this case also varies form one person to multiple persons in the scene.

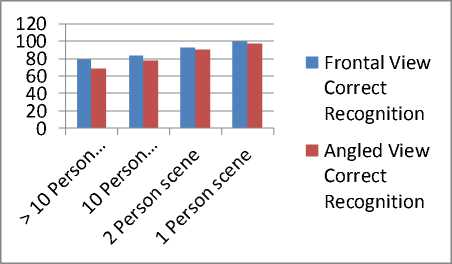
Figure 13: Recognition Results with varying angle of faces in varying audience in the scene

• VI.    CONCLUSION & FUTURE WORK

The proposed research work has implemented a face recognition system by using PCA which is eigenvector based multivariate analyses. Often, its operation can be thought of as revealing the internal structure of the data in a way which best explains the variance in the data. By implementing PCA the proposed Face Recognition System supplies the user with a lower-dimensional picture, a "shadow" of this object when viewed from its most informative viewpoint. The algorithm has been tested with multiple audiences in the scene and also captured faces at different angles in the scene. The algorithm delivers quite good results but there is a room to improve the algorithm performance in case of huge audience and also in the case of faces captured in the scene at some angle, so proposed system can be extended in the future to cover this aspect. The efficiency of the algorithm also can be increase further so there is also a room for future work in this area. The proposed system can be enhanced further in terms of achieving more efficiency by ease of analysis of patterns in the data.