Face Super Resolution: A Survey

Published Online May 2017 in MECS DOI: 10.5815/ijigsp.2017.05.06

Real-world applications involving face image/video analysis, biometric analysis, medical image analysis, remote sensing, etc. all suffer from the poor quality of the captured image. A viable enhancement is to super-resolve the low resolution (LR) input images/videos to high-resolution (HR) output images/videos. Two possible ways of actions are, either by enhancing the hardware or by enhancing the image quality using software. Using software-based techniques has been successful for past few decades. But, improving the hardware of the imaging equipment has proved to be costlier and carries more shot noise [1]. Face super-resolution (FSR), alternatively known as face hallucination (FH) is a super-resolution

(SR) problem, specific to a particular domain, that focuses on super resolving face images captured from surveillance cameras, or any other imaging system.

The algorithms formulated for SR cannot be applied to FSR due to the complex structural features in the face images. Techniques involved in FSR, pay much more attention to the structural details of the face. One of the pioneering works in FH was developed by Baker and Kanade [2]. A pyramid of features from LR images using Gaussian and Laplacian pyramids were used to reconstruct the HR image. However, the approach failed to model the face prior well, and also the facial HR suffered artifacts. A novel two-step approach invented by Liu et al. [3] processes a global model for retrieving the global structure of the face and a local model that captures the high-frequency details of the image separately and then integrates them to generate the HR image. A learning based algorithm for SR was suggested by Freeman et al. [4], that learns the association between the LR and HR images of the k-nearest neighbors (k-NN) of the input LR image.

Most of the methods in literature fail to accommodate all the variations that could be present in an image from the natural world, like disparity regarding illumination, pose, expressions, etc. This paper surveys some of the recent and state-of-the-art techniques in FSR. A brief overview of the imaging system used for FSR is discussed in Section II. The methods in the literature that work in the spatial domain have been reviewed in Section III.A and Section III.B. FSR methods in the frequency domain are discussed in Section III.C. Section IV consolidates the works discussed in the above sections with a subjective and objective analysis of their results. Section V concludes the work.

• II.    Image Observation Model

The image model is generated explicitly for testing the SR methods for its efficiency in the practical domains. The model generates the LR test images from the available HR images.

The LR image is created from a HR image by applying various image degradation forms like downsampling, blurring, noise addition, warping, etc. The general image model for single LR input image is depicted in Fig. 1. The original image is taken as the HR image and is downsampled to get an image of lower dimension. The downsampled image is further degraded by blurring it with a Gaussian kernel and adding noise to it. The degraded image acts as the input LR image for the SR technique. The reconstructed HR result from the SR method is compared with the original HR image to evaluate the SR technique.

Fig.1. Degrading HR image to form Single LR image

A similar model is adopted to produce multiple LR images (Fig. 2). The original HR image is degraded using downsampling, blurring, warping, noise addition, etc. To introduce multiple frames of the same image, linear transformations like rotation, translation, etc. are applied on the single LR image. Each frame differs from the other with slight orientations.

Fig.2. Degrading HR image to form Multiple LR image

The FSR problem can be put as; given an input LR image, find its corresponding HR image. This is an ill-posed problem as more than one HR image after degradation can be represented by the same LR image, i.e. a multi-valued association exists within the LR image and the HR image. So, a direct correspondence from LR to HR is hard. Predicting the correct association of the LR and its corresponding HR representation thus becomes crucial.

• III.    Face Super-Resolution Techniques

The input obtained from the imaging equipment can either be video sequence (multiple frames) or a single image. A single frame carries very limited information required for an accurate HR reconstruction. The reconstructed HR frame has more pixels when compared to the available LR frame. To fill in these missing pixels, a conjecture of the intensity values are performed to super-resolve the images. This technique of FSR from single frame input is called as Face Hallucination (FH). The missing data on the HR frame are estimated via learning mechanisms.

Contrary to single frame input, video/multi-frame inputs contain more information as they are images of the same scene with a minor distortion. The distortions/misalignment could be due to object or camera movement which could be fixed by a registration mechanism between the frames. Registration is a very crucial step, as it's accuracy has a direct influence on the resultant HR image. The better the accuracy, the better is the HR image quality. By registering the multiple frames onto a single frame and extracting information from different frames, an enhanced HR image could be reconstructed [5-7]. Even though FSR using single frame images are devoid of registration, the use of a vast and diverse training dataset is vital for its superior performance.

The most basic technique for hallucination would be to interpolate the given LR image to the desired HR image dimension. Widely used methods for interpolation are the nearest-neighbor interpolation, bi-cubic interpolation, interpolation using box kernel, etc. An interpolation based SR on natural images has been discussed by Shijo et al. [8]. However, interpolation based techniques lead to images that are poor in quality. Interpolation is better served as a sub-process in the super-resolution procedure. It is often combined with other techniques like learning and reconstruction. A major highlight of interpolation is its ability to retain the low-frequency details of the image intact.

The state-of-the-art techniques in FSR performed in the spatial domain can be broadly classified into two: Reconstruction based techniques and Learning based methods. The former technique mostly uses multiple frame input and reconstructs the final HR image from the various frames. While the latter learns the relationship between the HR and LR images of the training set to derive a mapping function and applies it on the input LR to generate its corresponding HR. A summarization of the notable FSR techniques using the Reconstruction approach is given in Section III.A. Section III.B summarizes FSR methods that adopt a learning-based technique for super-resolution. Other than the spatial domain methods, techniques that work in the frequency domain are briefed in Section III.C.

• A.    Super Resolution Using Reconstruction Techniques

Getting multiple images of the same person without illumination, pose and expression variation from realtime systems, like surveillance cameras, is nearly unattainable. Methods have been developed to use information from different image frames to reconstruct the HR frame. Each frame contains sub-pixel level information that could be combined with information from other such frames to reconstruct the HR frame. Fig 3 illustrates the structural model of the reconstruction based FSR.

Fig.3. Reconstruction-based FSR model

A general outline of the process can be summarized as follows:

• 1.    Multiple frames of the same scene may not be aligned with one another, so, as a pre-processing step, registration of the multiple frames has to be done. It has to be noted that the quality of reconstructed HR depends mainly on the accuracy of registration.

• 2.    Data from the registered LR images are interpolated onto the HR frame and optimized to yield the superresolved HR.

• 3.    A deblurring of the super-resolved output enhances the HR output.

The quality of the reconstructed HR image mainly depends on the registration accuracy. Imperfect registration results in a poorly reconstructed HR. To seizure, the complex structure of the face, Satiro et al. [9] states that optical flow technique is better equipped to capture the pixel motion between frames rather than parametric registration. As there is no training involved, all information required for the reconstruction of HR is to be extracted from the input images itself.

Various combinations of techniques have been used for each of the above mentioned steps. In [5], a unique method focusing on the shape of the face for registration is discussed. Multiple LR face images from a video are registered using Active Appearance Model (AAM). Then a reconstruction approach is adopted for the SR of the registered images. SR is applied on the illumination part of the image and combined with the chrominance part by interpolation. However, the method requires HR faces for detecting landmarks for the registration process.

A simultaneous SR and recognition (SSRR) method was proposed [10]. The model was initially developed to recognize a single LR frame and later, modified to work on several frames [6]. The given frames are distinct images of a person with the same pose and therefore belong to a single class. The method computes a template using features extracted from one class of images. A fitness measure of the template produces a feature space for the classifier to perform recognition. Recognition accuracy had increased when multiple frames were given as input rather than a single LR input. The method does not produce a super resolved image, but, directly uses the features extracted for recognition of the face.

Another approach to reconstruction-based FSR has been modeled by Satiro et al. [9]. The method detects the faces directly from the video sequence and pre-processes it to remove artifacts present during the face detection. Initially, a clustering is done to group similar LR frames based on the number of key point matches in SIFT features. For the SR step, frames in each cluster are registered using the optical flow technique onto a single frame within the cluster that has the best illumination. A blind deconvolution algorithm is applied to the registered image to deblur it. The deblurred image from each group is then fused using an alpha-blending procedure thereby producing the reconstructed HR.

In most of the reconstruction-based methods, the final HR image degrades as the magnification factor increases. As these methods do not include any prior information regarding the final super-resolved image, they are less significant in facial SR domain. Recent works combine both reconstruction and learning based techniques to outperform the state-of-the-art methodologies. Wang et al. [11] combines Iterative Back Projection (IBP) with PCA to reconstruct HR image with better quality. A framework based on IBP that preserves the high-frequency information which is usually lost during the degradation step has been proposed along with the PCA method to enhance the local high-frequency information. Initially, a wavelet transform for edge detection is performed to keep the edges intact and then a bicubic interpolation is applied to produce an estimation of the initial HR. The algorithm converges when the reconstruction error is minimized. Later, a PCA technique extracts more high-frequency information to enhance the result. The method converges faster by identifying and removing the acceptable pixel after every iteration.

Table 1. Summary of Reconstruction techniques

	[5]	[6]	[9]	[11]	[7]
Alignmen t Method	Active Appeara nce Model (AAM)	―	Optica l Flow	―	Face Trac -king
Regularization Term	Bilateral Total Variatio n	Tikhono v	―	―	―
Initial HR image estimatio n	Done during AAM	Interpolation	BI	BI	BI
No.    of Input frames	10	5	5	1	Multiple
Dependen t on	P,E, I	P, E	E	P,E,I	P,E,I
P: Pose Dependent, E: Expression Dependent, I: Illumination Dependent, BI: Bicubic Interpolation

Another method by Jia et al. [7] captures images from a surveillance camera using a face tracking algorithm. The captured LR and the eigenface generated from each

LR are combined using the sparse representation coefficients and added to the interpolated LR face to enhance the low-frequency details. Also, the high-frequency information is boosted up by an example-based SR technique using Approximate Nearest Neighbor (ANN). Computational time increases as training data increases. Enhancement incorporated by combining the global shape and the local high-frequency information results are empirically proven by Jia et al. [7]. Furthermore, the technique need not perform registration explicitly and avoids noise in the final HR.

Image alignment method for reconstruction from multiple LR images differs between each technique. The approximation of initial HR estimation from the given LR inputs can also vary. Other such factors that differ in each of the methods have been summarized in Table 1.

• B.    Super Resolution using Learning Techniques

Another category of FSR algorithms called Learning/Example based algorithms adopts learning mechanism to determine the relation that binds the HR representations with the LR representations in the training dataset. The coefficients required for producing a reconstructed HR from the input LR image are learned using a manifold learning technique. Manifold learning is a non-linear dimensionality reduction method. Most commonly used manifold learning method in FSR algorithms is the Locally Linear Embedding (LLE) [12], which finds the k-NN, using Euclidean distance, of the given LR representation and computes a weight matrix that can reproduce the input LR as a linear fusion of its k neighboring representations. The computed weight matrix is combined with the HR images corresponding to the k LR neighbor images to reconstruct the final HR image. It is assumed that the HR patches hold a similar local neighborhood structures like that of the LR patches [13].

Ma et. al. [14] points out that the non-feature information which contributes to a better super-resolved result is excluded when using dimensionality reduction methods like LLE, PCA, etc. A novel approach exploiting the position information of each patch is presented in the paper. Each patch of the input LR is reproduced by the union of patches at the similar position of each LR training image. The weight matrix computed and the HR patches at the same position of corresponding HR training image together reconstruct the final superresolved HR. In the case of noisy LR inputs, the method enlarges the noise content also.

The methods discussed in this section differ only in techniques used to super-resolve the input. Section III.B.1

summarizes few recent works that use sparse representation either for representing the features alone or the images as a whole. Section III.B.2 briefs out recent works using manifold learning and patch-position based learning. Learning methods including prior information of final HR image adopt a Bayesian framework for FH. Few of the Bayesian learning methods have been discussed in Section III.B.3. Some stand-alone non-conventional learning-based works in FH are also discussed in Section III.B.4.

• B.1.    Methods using Sparse Representation

A different representation scheme for image patches has been used in this category for FH. Traditionally, learning-based approaches work directly on the image patches sampled from the training LR and its corresponding HR images. But here, a more compact representation for the training patches has been formulated using the Sparse Representation. A basic outline of SR using sparse representation has been depicted in Fig 4. Samples of LR and HR patches from the training dataset form individual dictionaries D l and D h . Upon the arrival of an LR input, it is divided into patches, and similar patches are found from the dictionary D_l. These patches are sparse coded and combined with the sparse coefficient and dictionary D_h to reconstruct the final HR output.

Employing the fact that LR patches and HR patches have the same sparse representation, Yang et al. [15] proposes a two-step FH model. Initially, a non-negative matrix factorization (NMF) [16] is used to learn the subspace in parts. Then a coupled dictionary is used for the sparse representation of patches, and a patch-based learning is performed to get the super-resolved output face. The method fails to use the prior knowledge of the face thereby limiting the HR output regarding its visual clarity.

Instead of selecting a fixed K number of neighbors, an adaptive selection of neighbors is proposed by Jiang et al. [17]. To avoid the over-fitting or under-fitting condition that prevails, a locality adaptor is incorporated. By choosing the neighbors adaptively, the FH becomes more robust to noise.

An analysis to find the factor that improves face recognition using the sparse representation had been performed by L. Zhang et al. [18]. The investigation shows that collaborative representation gives more recognition accuracy. Based on this finding, Q. Zhang et al. [19] proposed a learning based FH. In addition to using the collaborative representation, a position based

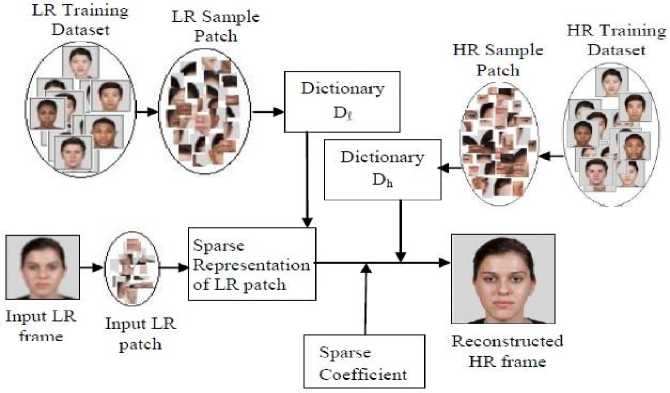
Fig.4. FSR model using sparse representation for dimensionality reduction

learning of LR and HR patches is employed in this method rather than learning a set of randomly selected patches. The resultant HR is constructed by integrating the HR patches according to their positions. The representation gives more recognition accuracy. However, it lacks in reducing the blurring effect of the reconstructed HR image. To overcome this flaw, image contrast enhancement is applied.

Instead of using two separate dictionaries for learning, a single dictionary implementation using K-SVD is discussed by Felix et al. [20]. In this method, the SR problem has been reframed as a missing pixel problem. The model considers the HR image as the interpolated LR image with many of its pixels missing from their positions, i.e. pixels from the LR image are placed at prespecified positions in the interpolated image. In this manner, different combinations of the pixels of LR can be generated to form the interpolated image. The resulting interpolated images are learned using the solo dictionary learning technique. A mean pooling of the recovered images is performed to produce the super-resolved image. A significant advantage of the approach is that the single dictionary need not retrain itself when magnification factor changes and also more details of the facial features can be reconstructed.

The sparsity in the representation scheme is brought in by the l 1 norm regularization term. A replacement for l 1 norm penalty in the conventional sparse representation has been suggested in [21] using the Cauchy penalty term. The Cauchy Regularization term is used to reduce the sparseness in the Sparse Representation for better hallucinated images. The method proves to produce more facial details when compared to other non-regularized methods. The resulting images are clear and similar to the original HR images.

Another work by Wang et. al. [22] presented a weighted adaptive sparse regularization (WASR) approach over the l1 norm regularization. A generalization of the l1 norm term to a general lq norm term helps to choose a proper sparse domain. The shrinkage parameter q of the lq norm regularization term is automatically approximated from the data to learn the linear coefficients for FH. This method shows a remarkable improvement in hallucinating images with noise for a q greater than 1.

Table 2. Summary of techniques using Sparse Representation

	[15]	[19]	[20]	[21]	[22]
Level	Patch	Positio n-patch	Image	Positio n-patch	Position -patch
Alignment	Yes	Yes	Yes	Yes	Yes
Position	Front al	Fronta l	Frontal	Frontal	Frontal
Patch-size	5x5	3x3	―	3x3	3x3
Coefficient	l 1 norm	―	Orthogonal Pursuit	Cauch y	Adaptiv e l q norm
Dependent on	P,I	P,I	P,E,I	P,I	P
P: Pose Dependent, E: Expression Dependent, I: Illumination Dependent

Table 2 summarizes the coefficient computation method used in different sparse representation techniques along with other factors differing in each of the methods discussed in this Section. The table also includes the dependency of each method on the input image specifications like the pose, expression, and illumination.

• B.2.    Methods using Neighbor Embedding

Neighbor Embedding (NE) [23] follows the conventional LLE approach. Fig 5 exhibits a general approach for LLE considering images as a whole. Euclidean distance between input LR image and images from the data set are computed to find its k-nearest neighbors. The given LR is represented as a fusion of these k-adjacent images. The coefficient matrix and the corresponding k-HR images from HR dataset integrate to reconstruct the HR output.

In NE, instead of taking each data point of the input LR image, the entire input image is divided into patches of fixed size and its k-NN corresponding to the image patch is searched in the training LR dataset. A brief description of the NE mechanism is as follows.

• 1.    Initially, a set of HR images is degraded (blurring, down-sampling, etc.) to form the LR training dataset. Both the LR and the HR training dataset images are divided into patches of fixed sizes.

• 2.    Given an input LR image, align it with the LR training set and then divide it into patches of fixed size. Take one LR patch at a time and find its k optimal neighbors using Euclidean distance. Compute the values

• 3.    Compute the final HR patches using the k corresponding HR samples along with the reconstruction weights obtained.

• 4.    Integrate all the HR patches linearly based on their position to form the resultant HR image. For pixels in the final HR that belong to more than one patch, its intensity values are calculated by averaging the pixel values.

  

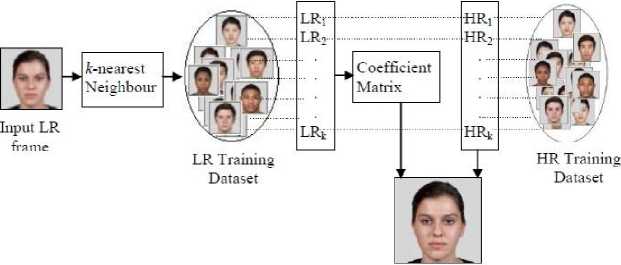
  Reconstructed

  HR frame

  Fig.5. FSR Learning model using Neighbor Embedding

  
  

needed for the linear fusion of k neighbors to form the input patch by reducing the reconstruction error.

Fang et. al. [24] uses an Adaptive Neighborhood Selection (ANS) instead of the k-NN technique to find the nearest neighbors of the input patch from the training set. Results show that the local geometry of the face manifold is captured accurately. In addition to using ANS, Deng et al. [25] uses a Dual tree complex wavelet transform to obtain the feature vector from the image. A position-patch based approach using ANS is used for learning the optimal nearest neighbors. Results show that sharper and more detailed images are produced when the neighborhood size varies for each test LR patch when compared with those algorithms that use fixed neighborhood size.

Nguyen et al. [26] proposes a double refinement of nearest neighbors by coupling LLE algorithm with Local Correlation Coefficients. In this, two methods are used to find the nearest neighbors of each patch of LR input. Initially, z-NN are calculated by the Euclidean distance. Further, a local correlation between the input patch and the z selected patches are done to determine the k true nearest neighbor. The reconstruction weights derived from the k-NN patches are used for reconstruction of the final HR image from the training set.

A frame alignment free FH has been presented by Li et al. [27]. The method involves a facial component-wise reconstruction using NE. The training and testing images are initially decomposed into five separate face components (eyes, nose, mouth, eyebrows and rest part). For every input LR patch of a component, its k-NN are identified from the training dataset. Then the reconstruction coefficients derived are combined with the HR patches to synthesize the HR output. The method can handle various poses and expressions.

A novel approach for alleviating the effect of illumination on the training and testing patches has been addressed in [28] by Song et al.. NE via illumination adaptation (NEIA) method initially aligns the testing and training faces through a dense correspondence, followed by an image decomposition approach to extract the illumination details from the images. Each training image is then adapted according to the illumination conditions of the testing image. The extended dataset, therefore, formed acts as the training set to identify the k-NN in the NE algorithm. The reconstruction weights thereby computed assists in synthesizing the final HR image. Results recover the edge details and the highlights of the image better. Extending the training set to incorporate the illumination details whenever a new LR image arrives is a major drawback.

Other than using the pixel intensity as a feature in NE, [13] introduced a method using the intrinsic features of the patches. Performing SVD on an image patch yields a unique single valued diagonal matrix representing the image. This matrix is used as the singular-value-unique (SVU) feature of the image. Including gradient feature makes the approach more sensitive to noise. Thus Tang et al. uses the Histogram of Gradient (HOG) as a feature to characterize the local geometry of the image patch. SVU combined with HOG forms the new coupled feature space. Combining the HR patches with the computed reconstruction weights, the super-resolved image is reconstructed.

Type of matching and features considered for matching in each of the methods discussed in the Section varies. Similarly, the patch size considered, the value of k (neighbors), overlapping pixels are all specific for each method. All these have been summarized in Table 3.

Table 3. Summary of techniques using Neighbor Embedding

	[24]	[25]	[27]	[26]	[28]	[13]
Align	Yes	Yes	No	Yes	Yes	―
Match	Patch	Positionpatch	Patch	Positionpatch	Patch	Patch
Patch size	5x5	5x5	―	3x3	―	16x16
K	10 60	3-20	9	―
Overlap	3	2	―	1	―	13
Feature	Pixel value	DTCWT of patch	Pixel value	Pixel value	―	SVU
Dependent on	P,E,I	P,E,I	I	P,E,I	P,E	P,E,I
P: Pose Dependent, E: Expression Dependent, I: Illumination Dependent

• B.3.    Methods using Bayesian Learning

The above discussed methods infer the output HR image from the given LR input and the training samples without any prior knowledge of the expected HR output. In the Bayesian approach, initially, a mapping function between the LR and HR images of the training dataset is learned as a prior model. Fig 6 shows a layout of the basic structure of FSR technique using the Bayesian framework. The learnt prior along with the likelihood is utilized to estimate the HR image for any given LR image by the following formula.

P(I H |I L ) = P(I L | I H ) • P(I H ) (1)

As mentioned earlier, predicting the correct HR image from the given LR image is crucial due to the one-to-many mapping. From the Bayesian theorem, a probability relation held by the given LR and the final HR can be defined as in equation (1). Maximizing the posterior probability P(I H |I L ) aids to find the optimal I H . A maximum a posteriori (MAP) criterion that maximizes the product of likelihood p(I_L | I_H) and prior P(I_H) is involved.

I H = argmax _Zfi P(I L | I H ) • P(I H ) (2)

To estimate the prior, it may require an extensive collection of training sample. So to avoid that, a two-step improvement to this methodology has been adopted. The global features representing the structure of the face and the local features representing the high-frequency details of the face are reconstructed separately.

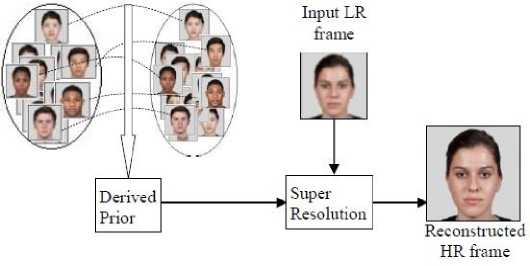
Fig.6. FSR Learning model using Bayesian Inference

Tanveer and Iqbal [29] have proposed a sample of this two-step approach for FH. Initially, the global structure is reconstructed using Direct Locality Preserving Projections (DLPP) with Maximum a posteriori estimator to estimate the high-resolution output. The second step involves an enhancement of the high-frequency details of the face using kernel ridge regression. Results from both the levels are combined to form the final super-resolved HR image.

Another approach [30] approximates the global structure of the reconstructed HR by estimating the coefficient vector from the low-dimensional domain using MAP estimate. The local enhancement is performed by basis selection on each facial part based on overcomplete non-negative matrix factorization (ONMF). Usage of ONMF guarantees better reconstruction of local facial features.

A novel approach for FH based on the alignment of the images was given by Tappen and Liu [31] using the Bayesian approach. The procedure initially picks up images similar to the input LR from the training set using a PatchMatch algorithm and then employs an SIFTFlow algorithm to find the correspondence between the selected images and the input LR. The SIFTFlow algorithm wraps each selected image from the dataset to the LR input. Finally using the Bayesian framework, the MAP estimate of the output HR image is computed. The method produces poor quality hallucinated images when warped examples are not similar to the input LR.

Innerhofer and Pock consider the alignment of selected images and input LR to be more important than the similarity between them for a better hallucinated image. Skipping the PatchMatch algorithm from [31] and applying the SIFTFlow algorithm for both selecting and aligning the images of training set has proved to give better results [32]. A fast converging primal-dual algorithm [33] with a unique solution is used for hallucination.

Li et. al. [34] proposed a nonparametric subspace learning technique in which the LR training images are clustered into k different groups using a nonparametric Bayesian method, distance dependent Chinese Restaurant process (ddCRP). Cluster centers are calculated by the mean of patches in that cluster. Regression coefficients that map to the corresponding HR patches are calculated. On arrival of an input LR image, the image is split into patches, and its corresponding similar clusters are found. Using the mapping coefficients found off-line, the HR patches are formed and integrated together to form the final HR image.

As discussed, the Bayesian framework requires a prior knowledge of the resultant HR image. Various prior have been considered in each of the techniques discussed. A summarization of the details regarding the prior used, level of operation of each method and its dependence on input specifications like pose, expression, and illumination has been organized in Table 4.

Table 4. Summary of techniques using Bayesian Framework

	[29]	[30]	[31]	[32]	[34]
Prior	Zeromean Gaussian	Prototype faces	Total variation norm	Total variation norm	―
Level	Patch	Image	Patch	Image	Patch
Face Position	Frontal	Frontal	Frontal and Profile	Frontal and Profile	Frontal
Align	―	AAM (semiautomatic)	SIFT Flow	SIFT Flow	―
Dependent on	P,E,I	E			P,I
P: Pose Dependent, E: Expression Dependent, I: Illumination Dependent

B.4. Other Learning Techniques

Example-based FH methods are time consuming process as the size of training dataset increases. The quality of the reconstructed HR mainly depends on the matched LR images from the training dataset. A mismatch could result in a poor reconstructed HR image. Avoiding these two problems, [35] has proposed an SVM based FH. The learning process is modified into a classification step, where the sample dataset is preclassified into subclasses initially. When an input LR arrives, the subset corresponding to the most similar PCA features of input is selected. The rest of the algorithm, after selecting the k LR images, works similar to example-based approach. This improvement reduces the chances of miss-match and also reduces the running time needed to choose the subset of LR images from the dataset.

A multi-layer framework for FH has been suggested by Tu et al. [36]. The approach considers an ensemble of facial regression functions to synthesize the final HR image. Each feature representation acts as a layer in the multi-layer structure. The interpolated LR image is given as input to the first layer. Each t^th layer takes in the input along with the learned regression functions to generate an output image that is fed into the (t+1)^th layer as the input.

The output generated by iteratively repeating this action until the last layer will be the final hallucinated image. The method is independent of variations in poses and expressions.

Usually, the given LR image/patch is structurally modified to a 1-D vector for processing, but this method proposed by Liu and Deng [37], processes the input LR image/patch maintaining its spatial structure as it is in 2D. A learning approach is performed in the 2-D space to derive the values needed to project the LR and HR patches onto a joint feature space. FH is performed using NE technique on this space to generate the initial HR and later a refinement is employed to enhance the output. One significant credit of the method is its ability to maintain the intrinsic 2-D structure of the input image.

Zhou et al. propose a network architecture based FH using Bi-channel Convolutional Neural Network (Bichannel CNN). A dual module framework consisting of a feature extractor and an image generator has been designed in [38]. Facial feature representations are extracted through deep convolutional layers to predict the intermediate images that are combined using a fusion coefficient to reconstruct the final HR. To deal with the information loss during the extraction phase; the feature representations are coupled with the raw input LR to generate a more enhanced hallucinated result. The approach is robust to unknown blurs and variations in illumination and poses and also has reduced artifacts in the result when compared to primary CNN. To improve the reconstructed HR quality by avoiding mismatch during the search, Huang and Tang also have proposed an FH method using Niche Genetic Algorithm [39]. Work on SR of natural images using Genetic Algorithm was presented in [40].

Works based on learning approaches provide better quality HR results when compared to reconstruction approaches. Learning methods consume more memory and computational resources for accommodating large training sets with a wide variety of faces. The compactness provided by sparse representation reduces the memory load but the time required to sparse code the entire dataset is another challenge. Most of the works fail to consider the image variations in pose, expression, and illumination. At the cost of memory and time, learning approaches can guarantee outstanding results.

• C.    Super Resolution Methods in Frequency Domain

An image can be considered as a 2-D signal or as a 2-D array of intensity values as most of the image processing works do. A few FSR techniques have considered the face images to be signals and have processed them in the transform domain. The LR input frame is initially converted to the transform domain. An SR technique valid in the frequency domain is applied on the image signal for extracting the approximate coefficients (AC) and detailed coefficients (DC). The AC and DC aid in preserving the edge details and the global structural details of the image. The coefficients are further processed to produce the resultant HR frame. An inverse transform is then performed to convert the HR frame back to the spatial domain. The output is post-processed to form the reconstructed HR frame. Fig 7 gives a brief pictorial representation of the same.

Even though most of the works till date have been developed in the spatial domain, there are reasonable works with good results in the frequency domain. The works in the transform domain are in Discrete Cosine Transform (DCT) and Wavelet domain. The significance being, DCT has good energy distribution representing the different visual quality in different subbands, and the Wavelet domain is insensitive to noise from raw images. The FH procedure in frequency domain combines learning mechanism along with it at some stage or the other. A few of the recent works in literature have been discussed below.

A formulation of the FH problem as a DCT coefficient estimation problem has been presented in [41]. An initial HR output is derived from the DCT coefficients of the LR image. The AC representing the low-frequency details are estimated from learning methodology based on Locally Linear Embedding (LLE) of k-NN and DC representing the high-frequency details is estimated by interpolation. To further enhance the HR output, a filtering mechanism that diminishes the artifacts from the result is also adopted in the post-processing stage. This approach reduces the size of training and testing sets. However, the algorithm is sensitive to variations in pose and expressions.

Another frequency domain FH method was discussed in [42]. The input LR is initially interpolated in the wavelet domain to the size of the final HR image. According to the lemma derived in the paper, a decomposition of the interpolated image into three different subbands and its reconstruction using Eigen transformations can result in a better hallucinated effect.

Input image resolution can become very low in real time instances, like in images from video surveillance cameras. Wang et al. [43] has suggested an FH algorithm based on improved DCT. The very LR image is initially interpolated to an intermediate resolution using Bi-cubic interpolation. Then, the intermediate result is processed similar to [41] to reconstruct the final HR image. The method, however, fails when the resolution of the input image becomes less than 12 x12 pixels. The major differences in the techniques are given in Table 5.

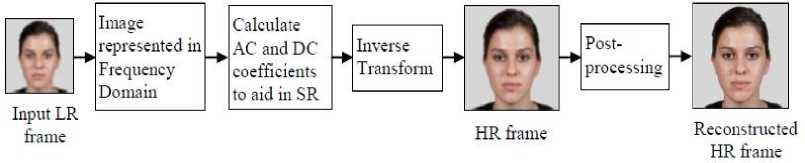
Fig.7. FSR model in frequency domain

Table 5. Summary of Frequency Domain techniques

	[41]	[42]	[43]
Frequency Domain	DCT	Wavelet	DCT
DC calculation	Cubic B-Spline Interpolation	Interpolation , eigentrans-formation	Cubic B-Spline Interpolation
AC calculation	MAP formulation	Eigentrans-formation	MAP formulation
Face Position	Frontal, Profile	Frontal	Frontal
Align	Yes	Yes	Yes
No. of coefficients	16/64	―	16/64
Dependent on	P,E,I	P,E,I	P,E,I
P: Pose Dependent, E: Expression Dependent, I: Illumination Dependent

• IV.    Discussions: Subjective and Objective Analyses

A general note on the strengths and weaknesses of each of the FSR methods discussed in this report has been tabulated in Table 6. Some of the papers discussed in each method, have overcome the shortcomings in them but with strict constraints on factors like, noiseless image, image poses, illumination, limited size, etc. A good algorithm that accommodates all the variations possible in real time scenarios has not yet been formulated. Active research is still going on for the same. FSR methods are more researched in spatial domain rather than frequency domain.

An analysis of the results provided by some of the works discussed above has been consolidated in Table 7. In most of the works, evaluation is performed on benchmark databases publically available. Specification of some of the databases has been given below.

• •    FERET: 14,126 facial images of 1199 subjects.

• •    CAS-PEAL: 99,594 images of 1040 subjects. Includes 5 variations in Expressions, 6 variations in Accessories and 15 variations in Illumination.

• •    CAS-PEAL R1: 30,900 images of 1,040 subjects. Includes 6 variations in Expression of 379 subjects, 6 variations in Accessories of 438 subjects, 31 variations in Illumination of 233 subjects and 2 to 4 variations in Backgrounds of 297 subjects.

• •    EXTENDED YALE-B: 16,128 images of 28 subjects. Includes 9 variations in Pose and 6 variations in Illumination.

• •    PUBFIG83: 8300 images of 83 public figures.

• •    FEI: 400 images in 14 different poses and illumination variations.

Each of the databases contains a collection of images that are regarded as HR images. These HR images are degraded by down-sampling, blurring and introducing noise to form a single/multiple LR images. The LR image acts as the input to the system. The super-resolved resultant HR image is compared with an original image from the database to check how well the system has been able to reproduce the original image. The evaluation can either be subjective or objective.

A subjective assessment is purely dependent on the human visual perception of the result, i.e., how well the faces can be identified. This result would vary from person to person, and its analysis on large scale of images would require more human resources. Whereas, an objective evaluation can be done quantitatively with assessment metrics like Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM).The more the PSNR and SSIM values, the more alike the reconstructed HR is to the original HR image. The need for FSR technique arises to improve the recognition accuracy in long distance images, but algorithms fail to illustrate the recognition accuracy for their work.

Table 7 displays the data collected from some of the works discussed in this report. The table exhibits the method, database used, input and output requirements, the power of magnification dealt with in each paper, Objective assessment metric: PSNR and SSIM (whichever is available), Subjective assessment: Ground truth and results from each paper. The contents of the table are entirely based on the information given in the respective papers.

Table 6. Strengths and Weakness of the different approaches in General

Frequency Domain			Pros	Cons	Factors affecting
			Parallel Operation	Blocking Artifacts	Spatial domain motion
			Low Operational Cost	Global Translational	Image Degradation
			―	Difficult to incorporate prior knowledge	―
Spatial Domain	Reconstruction		No learning	Degrades as magnification factor increases	Registration accuracy
			Less time	Loss of edge details	Similar frames needed
	Learning	Neighbor Embedding	―	Large memory requirement	―
			Better output quality	High operation cost	Local Geometry of LR and HR
		Sparse Representation	Compact Representation		Illumination, Pose and Expression
			―	Fixed k size introduces noise
		Bayesian Inference	Better Output Quality	High Operation Cost
		Other Learning
			Robust to noise	Sparse Coding takes time

A brief description of Table 7 is as follows: As face databases include a large variety of images in different lighting conditions, different camera distance, etc., we have decided to adopt a comparison based on the database used. A video sequence, Foreman, has been used in [9] and [27]. Each of the methods has extracted a single frame for the sequence and super-resolved them. [9] results in a less blur image; by adopting reconstruction (R) method, more information can be gathered from adjacent frames, thus higher PSNR. [27] has taken a profile pose rather than the frontal pose. The blurring caused may be due to higher magnification factor.

Three papers have worked on the FERET database. [11] has a higher SSIM but the resultant is blurred around the glass frame. [42] using frequency domain (FD) could still give a better PSNR than other two methods. The result of [26] is visually very poor due to blurring. This may be due to the magnification factor. The method fails to adapt to higher magnification factor.

Position-patch method in [14] performs poorly on images with accessories. The images in the database need not have the same accessory with the same structure. So position-patch learning performs poorly in this regard. It can be seen that the glass frame in the image is blurred around the corner of the eye and also the corners around the lips are blurred. [25] combines ANS and dual-tree complex wavelet to extract features to produce a better visual result when compared to [24] that uses only ANS. [37] has empirically proved that using the image as a 2D is more effective than converting it to 1D vectors.

• [ 28] adopts to the illumination changes in each input LR. The result has more lighting on the face when compared to the ground truth. [13] and [11] are evaluated on the same image. Using a DLPP with MAP estimator over HOG for recovering the global structure is better.

From the visual examination of [31] and [32], it can be inferred that SIFT flow is apt for selecting and aligning the LR images from the LR training dataset. As in [14], the sparseness fails to capture the accessories in the image. In [21], it can be seen that the lower part of the frame of the glass is not visible clearly. A generalization of the sparseness coefficient in [22] has increased its PSNR performance, but not visually.

Table 7. Subjective and Objective assessment of FSR techniques

Paper

Method

Database

Experimental Setup

Magni.

Result

Ground

Results

Factor

PSNR

SSIM

Truth

[9]

R

Video: Foreman

HR: 144x156; LR: 72x78

2

32.71

0.9235

[27]

L-NE

Video: Foreman

―

4

32.50

―

^

1

F^^

[11]

R

HR: 72x72; LR: 36x36

2

26.926

0.914

L2 1

1

[26]

L-NE

FERET

HR: 96x128; LR: 24x32; Training: 150/160

4

27.75

0.771

mb •*

[42]

FD

HR: 112x96; LR: 56x48; Training: 180/360

2

28.66

0.8759

J

^

L

[24]

L-NE

CAS-PEAL

HR: 128x128; LR:32x32; Training: 1000/1030

4

33.4

―

К 1

r 1

[14]

L-NE

HR: 128x96; LR:32x24; Training: 270/300

4

29.2

―

fe^

[25]

L-NE

FERET, CAS-PEAL

HR: 256x192; LR: 64x48; Training: 500/600

4

32.796

0.92

[37]

Other Learning

CAS-PEAL R1

HR: 256x128; LR: 64x32; Training: 940/1040

4

35.83

0.976

l^

[28]

L-NE

Testing set consists of face images with different pose and illumination

4

34.03

―

tsi-

e

[13]

L–NE

Extended Yale Face B

HR: 192x168; LR: 48x42; Training: 28/38 subjects

4

32.266

0.9088

[29]

L–B

HR: 112x112; LR:28x28; Training: 415/425

4

―

0.9506

[31]

L–B

PubFig83

HR: 100x100; LR:25x25

4

24.05

0.748

Г" -д

[32]

L–B

HR: 100x100; LR:25x25

4

24.13

0.75

[21]

L-S

FEI

HR: 120x100; LR: 30x25; Training: 360/400

4

32.51

0.91

5# II51

[22]

L-S

HR: 120x100; LR: 30x25; Noise Free images

4

32.93

0.917

Г"1

Fl

FD: Frequency Domain, R: Reconstruction, L-NE: Neighbor Embedding, L-B: Bayesian Learning, L-S: Learning using Sparse Representation

• V.    Conclusion

As the demand for better image quality from acquisition systems is growing, the pressure is on developing better algorithms that utilize fewer resources such as time and memory in a minimal manner. Many algorithms proposing a solution for the SR problem have been studied in the literature, but the problem still suffers from poorly reconstructed HR images due to limited information from LR image. In this paper, a brief survey on the recent methodologies in FSR has been done. The works reviewed are categorized on the basis of the number of input frames available, processing domain and the methodology used. A comparison table of the subjective and objective results from some of the recent papers has also been illustrated.

Frequency domain techniques have low computational requirements and amenable for parallel implementation, but suffer from blocking artifacts. Performance is affected by spatial domain translation and image degradation.

Spatial domain reconstruction approaches do not require any learning, and hence faster. However, increased magnification factor causes degradation, and non-preservation of edges. The approach requires accurate registration and availability of similar frames.

Learning techniques, in general, provides better HR quality, though the computational cost is high. However, the performance of Bayesian learning and sparse representation learning is affected by illumination, pose, and expression. Though neighbor embedding provides better performances among the learning based techniques, it demands large memory and is affected by local geometry of LR and HR images.

The focus of future research on learning based techniques, such as neighbor embedding and sparse techniques, is expected to lead to low complexity approaches providing better performances. Moreover, a combination of reconstruction techniques and learningbased techniques would provide a more promising result with better recognition accuracy. Introducing relevant pre-processing and post-processing steps could further enhance the algorithm giving more accuracy in recognition systems. As the area has got immense scope for applicability in real-time scenarios, more effort is expected to be put in this direction.