Facial expression recognition by holistic and geometrically integrated subspace

Published Online November 2018 in MECS

Facial expression recognition is a cognitive task for various applications where one can understand the human internal feelings. Drowsiness of vehicle driver can be recognized with suitable facial expression recognition approach. Accuracy of human expression recognition depends on the situation of face image has taken. The mobile sciences, medical diagnosis, mind training, psychological studies, security based systems all have different views of the facial expressions Plutchik emotional model presented in [1] illustrates the relationship between one to one emotions generated by different expressions. Ekman and Friesen [2] proposed Facial Action Coding System (FACS) for expression recognition during 1978. Ekman [2] was categorized the expressions based on distinct properties of faces as anger, happy, sad, surprise, disgust and fear. Facial expression recognition for static images of three different databases have been utilized in this work for comparing the related works as mentioned in next section. In this work section 2 demonstrates related work, section 3 focuses on proposed frame work, section 4 delivers brief overview of subspace manifolds, section 5 discuses about results and analysis. Conclusion is drawn in section 6.

• II.    Related Work

  Peng et al. (2005) [3] worked on facial expression recognition and classification using minimum redundancy –maximum relevance method which has been based on mutual information to select the subset of features during reduction of features space. Bai et al. (2009) [4] they combined LBP features and Gabor features of face images. For efficient expression recognition they used weighted LBP Gabor complex features with linear discriminant analysis. Yu and Yang [5] used discriminative approach to recognize the face by discarding null space from between class matrix and diagonalized the within scatter matrix in order to solve the problem of singularity matrix. Xie et al. [6] presented Gabor based feature extraction by separating Gabor magnitude and phase parts separately. Phase part has been modified by introducing local Gabor exclusive OR patterns. They carried out expression recognition by reducing the high dimensional space by introducing block based Fisher linear discriminant analysis. In our work a novel approach for fusion of extracted features based on geometrical and appearance methods have been proposed. Geometrical eigen feature vectors have been generated for limited areas of face part.

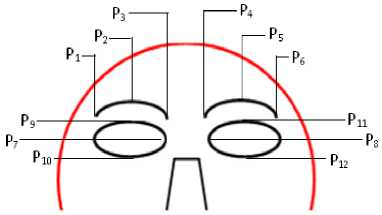
Fig.1. Locations of fiducial points on upper part of the face image

extraction by considering magnitude and phase parts separately for face recognition application. Both magnitude and phase feature vectors were projected by Fisher LDA algorithm. Linear Fisher Discriminant Analysis for face recognition has been demonstrated by Sugiyama et al. [51]. In our work linear and nonlinear discriminant based subspace methods have been utilized for reduction of high dimensional data to low dimensional data. Different scales and orientations of Gabor filter has been utilized for construction of high dimensional combinational based feature dataset.

According to several literatures it can be viewed as Linear Discriminant Analysis (LDA) method can be used for expression recognition for different databases. If number of expression data samples reduces then performance of LDA algorithm becomes fall down and scatter matrix also becomes singular. Hence it would be difficult to maintain larger variability between two classes. Optimization for the singularity matrix problems were noticed by Belhumeur et al. [7] and proposed a Fisherface method (FF) , which uses a principal component analysis (PCA) [15] [53] based projection strategy. Li et al. [8] did discriminant analysis based non parametric approach recognition. Ming et al. [9] proposed spectral regression kernel discriminate analysis (SRKDA), and suggested that SRKDA method can efficiently yields better solutions than ordinary subspace learning approaches. Rahulamathavan et al [10] introduced facial expression recognition system with encrypted domain using linear Local Fisher discriminant analysis (LFDA). Author was tested JAFFE data base with the developed algorithm and achieved 94.37% recognition rates. Happy and Routray [11] worked on patch based strategy for different face appearances. For expression classification discriminative features were considered by further patches obtained from active patches. Feature extraction by Gabor filter with local binary pattern and dimensional reduction of high dimensional data concept is introduced by Abdulrahman et al. [47]. Liu et al. (2012) [48] has been carried out facial expression recognition based on the fusion of geometry features and texture features. Deng et al. [52] demonstrated about local Gabor based feature extraction with LDA and PCA projection. Zhen and Zilu [53] tested JAFFE database using fusion approach which was framed by Gabor filter and 70% of overall recognition accuracy has been achieved.

Linear and nonlinear subspace projection methods were directly implemented by some researchers on input image dataset to achieve feature extraction and dimension reduction. Different subspace methods were implemented on high dimensional feature dataset for dimensional reduction and compared the consequences of subspace methods [12]. George et al. [13] worked on facial expression recognition with SMS alert. Various state of art on facial expression recognition system was made by Bettadapura in [14]. One of the most popular and old subspace methods such as principal component analysis (PCA) [15-20] has been used in this work for projection of Fisher linear discrimiant subspace [38-42]. Struc and Pavesic [21] worked on Gabor filter based feature

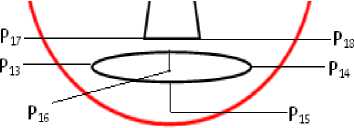
Fig.2. Locations of fiducial points on lower part of the face image

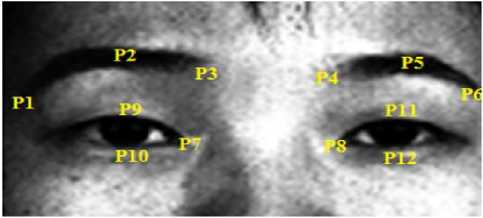
Fig.3. Upper part of the face and pre-marked fiducial points

• III.    Proposed Feature Level Fusion

In this work total Gabor filter space has been divided in to two separate spaces such as Gabor filter magnitude space and phase feature space [21]. These two feature vectors have been fused with extracted geometrical feature vectors. In this section a novel approach for fusion of feature extraction have been proposed. Geometrical feature extraction has been carried out with a new concept of limited regions of the face which is compatible with textures features during the fusion of extracted features. Geometrical features are essential for expression recognition and classification. These features changes whenever the face region gets deformed with different movements in the muscles of the face. Region of interested areas have been selected from different face templates and some fiducial points were located on face image. Basic architecture of entire expression recognition system based on extraction of both geometrical and holistically extracted features supports efficient recognition and classification of expressions after subspace projection. Both geometric and holistic features are key elements for final expression recognition.

In this paper geometrical feature has been extracted which is related to AAM model [22] feature extraction approach, points are marked on corner point of eyes, where the upper and lower eyelid meet called eye canthus.

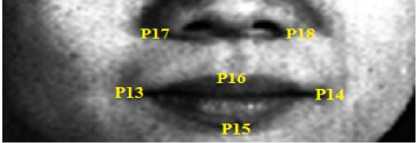
Fig.4. Lower part of the face and pre-marked fiducial points

Pre marked points on upper face and lower face parts yields geometrical features, which supports texture information. Figure 1 and Figure 2 shows location of fiducial points on face. In this work 18 fiducial points has been located on face image and 16 dimensions eigen vectors has been computed as given in (3). In upper face part P 1 to P 12 points were marked by selecting eyes and eyebrows face templates as local points. In left eye brow P 1 , P 2 , P 3 points were marked and in right eye brow P 4 , P 5 , P 6 points were marked respectively as shown in Figure 3. Some points like P 9 , P 10 , P 11 , P 12 are marked on upper and lower eyelids respectively on both the eyes. Corner points of eyes are P 7 and P 8 . Variation of eye brow and eyelids movements makes the different values of eigen values. Points P 7 and P 8 are to be considered as inner canthi on reference points.

In lower part of the face nose and mouth templates have been considered, two extreme ends of lip were marked by points P13 and P14 as shown in Figure 4. Middle points of the lower and upper lip were marked as P15 and P16. Some of the expressions are exhibited based on compression and expansion of nostrils position. The magnitude of eigen vector and meaning of each geometry features are showed in Table 1. In this Table, mi ( P1,  .  .  . ,P18) is the abscissa of ith point and ni( P1, ....P18) is the ordinate of ith point ( a point where the pre-marking has been done).

E = । m⁸ ^ nP\             (1)

Where E is a reference value or base value is a constant in magnitude. Base E is the central point of the two inner canthi. In respect that the inner canthi (point P7 and P8) are constant in 18 feature points, these points are considered as the reference points, and then 16dimensional eigenvector {EG1, EG2, EG3 ....EG16} are obtained. During experiment validation {EG1, EG2, EG3 ....EG16} has been used as facial expression eigen value features feasibility analysis.

For all the databases eigen feature based geometrical feature extraction procedure has been implemented. Geometrical Feature Eigen Vector (GFEV) is computed as follows.

GFEVupper = [EG1, EG2, EG3......EG12]

GFEVlower = [EG13, EG14,.....EG16 J

The total dimension of geometrical feature vector (GFV) is 16 is given as

GFV = [EG1, EG2,.....EG16 ]

Magnitude part of the Gabor filter has been enhanced by combining Gabor filter magnitude feature vector with upper face part geometrical features. Similarly phase part of Gabor filter has been enhanced by combining Gabor filter with lower face part geometrical features. Gabor magnitude feature vector (GMFV) is fused with Upper face geometrical feature vector (GFEV upper ) and Combinational Gabor Magnitude Feature Vector (CGMFV) have been formed. Similarly Gabor phase feature vector (GPFV) is fused with lower face geometrical feature vector    (GFEV_lower)    and

Combinational Gabor Phase Feature Vector have been formed. Proposed expression recognition system using feature level fusion and discriminant based subspace methods presented in Figure 5. Feature level fused dataset of both combinational Gabor magnitude and combinational; Gabor phase has been projected using different linear and nonlinear subspace methods. Projected subspaces of both CGM and CGP were fused using score level fusion and Combinational Entire Gabor (CEG) subspace has been formed. This CEG subspace has been computed for both training dataset images and testing images respectively. Euclidean distance have been computed between final score matrix of both the train and testing CEG subspace. Based on the Euclidean distance metric expressions were recognized. All the expressions were classified using “Leave One Out “strategy of support vector machine classifier. Table 1 presents Eigen values of geometrical feature vectors for upper and lower face part.

Table 1. Eigen values of geometrical feature vectors for upper and lower face part

Magnitude of Eigen vector	Equivalent meaning	Magnitude of Eigen vector	Equivalent meaning
EG 1	I Ур1 - E l	EG 9	I yP12 - ^11|
EG 2	1 Ур2 - E l	EG 10	| УР 13 - E|
EG 3	1 Ур3 - E l	EG 11	I Ур 14 - E|
EG 4	|XP4 - хр	EG 12	| УР16 - e|
EG 5	1 Ур4 - E|	EG 13	Ур16 - Ур 15
EG 6	1 Ур 5 - E|	EG 14	xP 14 - P 13|
EG 7	1 Ур6 - E l	EG 15	| Ур 17 - E
EG 8	| УП0 - P\	EG 16	|Ур 18 - E|

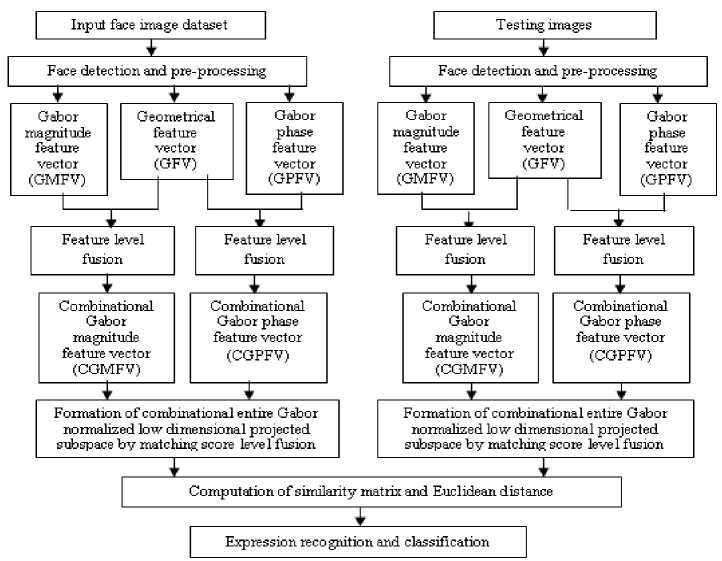
Fig.5. Methodology of the entire work

• IV.    Overview Of Subspace Methods

In this section brief overview of subspace methods have been discussed. Subspace methods finds vital role for dimensional reduction of higher dimensional data. Curse of dimensionality is a problem for subspace projection. Principal Component Analysis subspace method has been implemented on proposed feature level fused dataset for different values of dimensions of images with different values of Gabor filter scales and orientation values as parameters.

• A.    Subspace Formation

In this work PCA has been framed and made it into increases the sample variances by reducing correlation between data vectors. PCA is a dimensional reduction subspace method and relatively simple. It speeds up the computational time during recognition of expressions moderately. High dimensional data has been decorrelated by PCA method. In this method class variables are not used. Due to this reason PCA is unsupervised. It preserves global structures of data by maximize the variance. It uses second order statistics by referring orthogonal space analysis. This method basically lies on eigenface concept. Consider a combinational Gabor dataset G, which consists of N measurements gj (1

w 5/gi- gг

1N g = N=$1 gi(6)

Where g is the mean value of combinational Gabor feature dataset of G samples.

FLDA algorithm was developed by P.Belhumeur et al. [7]. It surplus the performance of eigenfaces (PCA) approach , in some cases FLDA works well even if different illumination occurs with lower error rate. Also works well even if different facial expression takes place. FLDA maximizes the between-class scatter matrix variance and minimizes the within-class scatter matrix variance. FLDA finds vital role as a basic strategy in discriminant based approaches for expression recognition and classifications. When number of features in feature space becomes larger than the number of training samples, then within scatter matrix becomes more singular. Limitation of number of training samples causes this singularity problem. In this work high dimensional combinational Gabor dataset has been reduced by class discriminative subspace approaches by referring our earlier work mentioned in [12]. In FLDA between class matrix S b can be given as

• ^Sb = $ ^Ni ( gi - ^g )( gi - ^gT         (7)

i = 1

Within class scatter matrix S w be defined as

Sw = | ( Ni - 1 Si = | I ⁽ gi , j - gi ) gi , j - giT (8) i = 1 i = 1 j = 1 ^{v J}

Where g_i, j is the n-dimensional pattern j from class C_i, and N i is the number of training pattern from class C i , and C is the total number of classes or expression groups. The total meanvector is given by

^g = N C Ni              ⁽⁹⁾

C Ni gi = NIaij            (10)

Vector a _i and matrix i are the unbiased sample mean and sample covariance of matrix of class. In above equation (9) and (10) where N is the total number of samples, that is N=N 1 +N 2 +N 3 + - - - N C .

Locality Preserving Projection (LPP) approach [43-46]preserves local features of input data obtained from affinity matrix (similarity graph information). The input data are projected as same as PCA manner ie S=W^TG. During the preservation of local contents LPP method minimizes the different object function by putting large penalty on neighboring points g i and g j if both are mapped with larger difference in projected space.

GLGTWk = X _kGDG^TWk         (13)

Locality preserving projection based Fisher discriminant Analysis (LFDA) is explicitly preserves the local discriminative features by labeling the classes of different expressions. LFDA is a dimensional reduction method of multimodal data by preserving the local structure of within scatter matrix. By increasing between class scatter matrix variances. For larger variations of features of expressions occurs linear methods fails to give good strength for efficient recognition and classification of expressions. Following section illustrates briefly the three different discriminative based nonlinear subspace approaches. Consider set of combinational Gabor feature dataset G. where

G = g , •••• gN ] e RmN         (14)

The objective function of combinational entire Gabor LFDA is given by

argmax Z^TS^bZ

Z  ZTSwZ

min                   2

W_ti , ¹ jki-WUA

Where S^b and S^w indicates the local inter class scatter matrix and local intra class scatter matrix respectively. W_i^b_j and W_i^w_j indicates the weight matrices of the local inter class adjacency graph and local intra class adjacency graph respectively. C i is the class label of the data point g i and l e { 1,2, • • • C } is the class label I this worl heat kernel weight has been used for constructing affinity graph such as A fij

k = 1,2,-- d

Where ^ ij is the weight of the connected edge between neighboring points g i and g j in the affinity graph. Two common methods like heat kernel and cosine model are implemented for computing the value of £ j in the input space. If two points are not connected in a same neighborhood then £ ij =0. Locality preserving uses affinity graph to compute an optimal projection in an effort to preserve the local structure of the data. The objective function can modified as

Sb = 1, N ^wbj ( gi - gj '(Si - gj T       (16)

² i , j = 1

Sw = 1 I W^ww l gi - 8j '(.gi - gj'T       (17)

² i , j = 1

Wb = {

^Afij\. iN - NN-)-fCi = Cj = ^l ; vfCi • Cj

min W_k

WkTGLGTWk

s.t.

wTGDGTWk = 1 (12)

Ww = \ Nl ’

A

-Nijr ,^fCi = Cj = ^l ;

0, ifCi * Cj

Where L D- c is the Laplacian related graph, and D is a diagonal matrix with Du = | j^y . Then computation of the required projection of subspace solution is obtained from following eigen value problem definition.

Final eigen vectors corresponding to maximum eigenvalue of the generalized eigenvalue problem is obtained from (15) and given as

SbZ = ASwZ

Objective functions of KLFDA [50], KLSWFDA and KGLSWFDA are found by referring our earlier work as mentioned in [23]. All the subspace methods are used to reduce the dimensionality of combinational Gabor space. The reduced dimension space has been named as combinational entire Gabor (CEG) subspace. Expression recognition using all the subspace methods have been named as CEGPCA, CEGICA, CEGFLDA, CEGLPP, CEGLFDA, CEGKLFDA, CEGKLSWFDA and CEGKGLSWFDA approaches respectively [please refer our earlier work given in open access article [23] [24]).

• B.    Creation of CEG Space

Similarity score matrix of combinational Gabor magnitude (CGM(Subspace) S and similarity score matrix of combinational Gabor phase (CGP(Subspace) S has been computed. Normalized score of combinational Gabor magnitude subspace can be given as

NSCGM ( Subspac'e

CGM ( SubspaceS - h(CGM Subspace s)

Std(CGMSusbpaceS )

Normalized score of combinational Gabor phase subspace can be given as

N^SCGP ( Subspace

CGP ( SubspaceS - P(CGP.Subspace s)

Std(CGPSusbpaceS )

Final score subspace matrix [25] can be obtained by fusing both CGM and CGP normalized score matrices using maximum fusion rule.

testing expression image is matched with trained image. Based on Euclidean distance metric and RBF kernel based SVM classifier [26] facial expressions are classified.

• V.    Results And Discussions

• A. Database Used

• •    JAFFE database: In this work, Japanese Female Facial Expression (JAFFE) database was used for experiment [27]. Figure 6 shows cropped samples of JAFFE database. Total 210 images were cropped into 111x126 size. Only required areas like mouth nose, eyes and chin areas has been considered during face detection for extraction of texture features and rest of the part was removed.

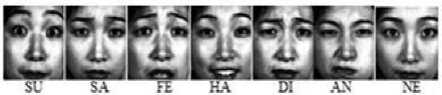
Fig.6. Cropped and preprocessed images JAFFE database

W^{CEG (} Weighted Subspace)  M^^ H NSCGM ( Subspace) ⁺ NSCGP ( Subspace)

Euclidean distance between trained and test image dataset have been computed

Fig.7. Cropped and preprocessed images JAFFE database

^£ i

WCEG(W _ Subspace ) Q - WCEG ( W _ Subspace ) T

Where  WCEG(W_ Subspace)T  and WCEG(W-Subspace)Q are projected vector final score weight matrices of training and testing combinational entire Gabor subspace images. The image set with lower Euclidean distance is computed. Re-perform the operation on this image set with lower threshold value to get the image having the expression closer to the defined image. The image with smaller value of Euclidean distance in between score matrices of both trained and testing expression images will be represented as the resultant expression image. So that

• •    FD database : This database (FD) consists of 13 subjects and each subject has 75 images with different expressions. In this work 500 images were used with 10 subjects, five expressions such as happy, surprise, angry, sad and neutral. Each class of expression has 100 images. For experiments, all the images are preprocessed and the size of these images is scaled down to 92 x 92 pixels size shown in Figure 8.

Fig.8. Sample images of FD expression database of size 92 x 92

Table 2. State of art approaches of JAFFE database