Facial Image Super Resolution Using Weighted Patch Pairs

Published Online March 2013 in MECS

The ever increasing demand on surveillance cameras is quite visible nowadays. Some major users of such technologies are the banks, stores and parking lots. When using security cameras or cameras recording far distances, we usually face low resolution - low quality facial images. These images do not have sufficient information for recognition tasks or other usages and require a boosted upgrade in their resolution quality. Because there are always the high frequency details that carry the typical information used in processing techniques. This upgrade is performed with different automatic or manual process.

Surveillance and monitoring systems like many other video based applications must extract and enhance small faces from a sequence of low-resolution frames [1], [2]. Direct interpolating of the input image is the simplest way to increase image resolution with algorithms such as cubic spline or nearest neighbor. But on the other hand the performance of direct interpolation is usually blurry and poor since no new information is added in the process.

The process of increasing the resolution in images is called Super resolution. If the image that is being super resolved is a human facial image, the process in this special domain is called face hallucination. The term "face hallucination" was first coined by Baker and Kanade [3-4]. This is a borrowed term which is originally a medical phrase that is used to describe a common symptom of severe mental disorder in patients who have visions or imaginary perceptions which does not exist. The purpose of this naming is that in Baker and Kanade’s method, the output image will have high frequency facial hallucinated details that are not available in the LR image. Super resolution has diverse applications such as in medical images, aerial images, surveillance cameras expanding web images, improving old pictures, converting NTSC television images into HDTV and etc.

There are two main methods in resolving LR images. The first method is using reconstruction-based methods and the second one is using learning-based methods. The former method uses a sequence of images as the input and reconstructs an output image by the multiple inputs. The latter method uses learning, created by given previous given information from a database to form a higher resolution image from the input LR image.

The proposed method relies on the second method. Our main aim in face hallucinating is to reach a high quality super resolved image from the LR single frame input image. Since face detection is one of the important research issues by itself and needs its own algorithmic and conditional considerations it will be remained beyond the scope of this paper and the input images will all be previously extracted and cropped manually. Extensively surveyed papers on face recognition are presented by Yang et al. [5] and Kakumanua et al. [6]. The given cropped facial image is the input of the hallucination algorithm as shown in Fig. 1.

Fig. 1 An example of a low resolution single frame facial image: a) cropped facial region b) cubic spline interpolating c) desired HR image.

(a)

(b)

(c)

Prior work on face hallucination will be discussed briefly in section 2. The creation of image patches and the overall proposed system is discussed in section 3. The steps on creating the learning database come after that and then there are experimental results. Finally the concluding texts are the ending sections.

• II.    Related Works

The first two to propose a "recognition-based" superresolution (SR) method in their literature were Baker and Kanade [3-4]. In their pixel-wise method, it infers the high frequency components from a parent structure with the assistance of training samples. Their technique precisely functions by disintegrating an image into a pyramid of features including the first and second derivatives of the Gaussian pyramid and the Laplacian pyramid, and then searching the nearest neighbors of each pixel in this pyramid through a training dataset. In order to generate the target HR image, the high-frequency pyramid features for the input pixels are selected based on maximum a posteriori (MAP) formulation of the LR improvement problem.

A non-parametric patch-based prior along with the Markov random field (MRF) model to generate the desired HR images was executed by Freeman et al. [7]. By applying a homogeneous MRF model to learn the statistics between low-resolution "image" patches and underlying high-resolution "scene" patches, and the relation between neighboring "scene" patches, a framework for handling low-level vision tasks were implemented. The model is applied for generic image super-resolution when the scene and image are high- and low-frequency bands respectively.

Liu et al. [8] propose to integrate a holistic model and a local model for SR reconstruction. The performed two-step approach is executed by integrating a global parametric model with Gaussian assumption and linear inference and a nonparametric local model based on

MRF. Both of the two methods used complicated probabilistic models and were based on an explicit resolution-reduction-function, which is sometimes unavailable in practice [9].

Inspired by a well-known manifold learning method, Locally Linear Embedding (LLE), Chang et al. [10] implemented the Neighbor Embedding algorithm based on the assumption that small patches in the low- and high-resolution images form manifolds with similar local geometry in two distinct spaces. The local distribution structure in sample space is preserved in the down-sampling process, where the structure is encoded by patch-reconstruction weights.

Wang and Tang [11] suggested a face hallucination method using principal component analysis (PCA) to represent the structural similarity of face images. They considered the face hallucination problem as a transformation between different face styles. The implemented method used PCA to fit an input low-resolution face image to a linear combination of low-resolution face images in the training set. A high-resolution image was then rendered by replacing the low-resolution training images with their high-resolution correspondences, while retaining the same combination coefficients. However, this method only utilizes global information without paying attention to local details.

Park et al. [12] proposed a technique derived from example-based hallucination methods and morphable face models. They proposed a recursive error back-projection method to compensate for residual errors, and a region-based reconstruction method to preserve characteristics of local facial regions. Then defined an extended morphable face model, in which an extended face is composed of the interpolated high-resolution face from a given low-resolution face, and its original high-resolution equivalent.

An example-based Bayesian method for 3D-assisted pose-independent facial texture SR was introduced by Mortazavian et al. [13] Bayesian framework was implemented to reconstruct a high-resolution texture map given a low-resolution face image. Their method utilizes a 3D morphable model to map facial texture from a 2D face image to a shape- and pose- normalized texture map and vice versa.

• III.    Weighted Patch Pairs Super Resolving

The process of creating HR for LR input images while adding high frequency components to the image is similar to solving a mathematical problem with "m" equations and "n" unknown components while the quantity of the unknown components compared to the quantity of available equations are much more. This process is almost impossible unless we moderate the problem by narrowing down the domain into a specific application which in this special case is the human face domain. Since face images are well structured and have similar appearance, they span a small subset in the high dimensional image space [14]. This similarity can be more obvious when comparing texture and color of the skin or the shape of the eyes, nose, lips and the space between them in human facial images within the same race, sex and age. Utilizing the faces structural resemblance, implies that the high frequency detail can be inferred from the low frequency components. On the other hand human facial features vary from one person to other especially depending on their age, sex and ethnicity. And even in the same mentioned conditions human faces have a great appearance variety. This makes using holistic and global methods to act very poor without having the ability to create certain specific high frequency components in the facial image which act as visible traits for human based and machine vision recognition. Hallucination face images by the aid of weighted image pairs patches helps to improve the resolution of such images without blurring the image or giving a mean global output.

• A.    Creating the Patches

The two dimensional input image will be converted into a vector of the pixels at the first stage. Each image pair in the database was created by one HR image with its low quality image that is the smoothed and downsampled image of the HR pair. Both high and low resolution images are disintegrated into fixed size image patches with defined locations and with an overlapped region with their neighbor patches. Each LR image patch will be a pair for its corresponding HR patch. The ratio of the size of the LR patch to HR patch is proportional to the ratio of the HR image to the LR image. Each patch will be reshaped into a vector for further process. Each facial image will be considered as a matrix like { X M ( i , j ) } " ₌ ] made of overlapping image patches where N is the total number of patches in image X . The patch in row i and column j in the patch matrix is mentioned by X^M ( i , j ). Assume that each square patch fills n x n pixels. For the LR image { X M ( i , j ) } N ₌₁ if n is an odd digit, the patch X M ( i , j ) will be overlapping n x [( n -1)/2] pixels with its neighbor patch and for its proportional HR image the patch X M ( i , j ) which fills qn x qn pixels will have overlapping on ( qn ) x [ q ( n -1)/2] pixels. And if n is an even digit, the patch X M ( i , j ) will be overlapping n x ( n /2) pixels with its neighbor patch and for its proportional HR image the patch X M ( i , j ) which fills qn x qn pixels will have overlapping on qn x ( qn /2) pixels. An example of the creation of facial patch is shown in Fig. 2.

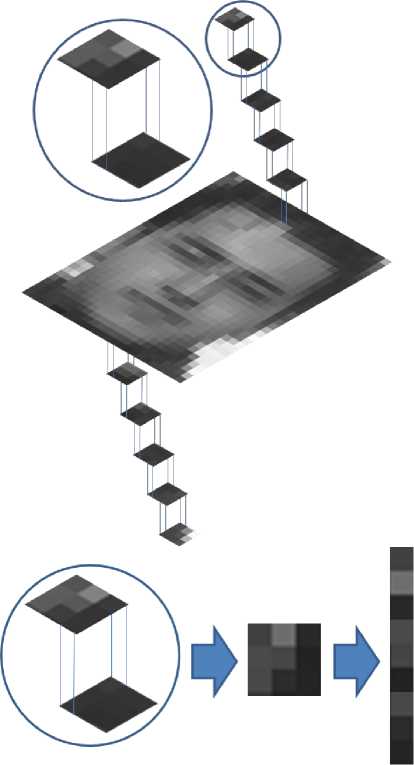
Fig. 2 Creation of the patches from the facial image

• B.    Reconstruction Based on Patch

Assume that X^p stands for the available learning database images having p =1,2,..., P where P is the number of these images. Each patch in the learning database will be in the form of { X^pM ( i , j ) } N₌₁ .

The reconstructions weight matrix will be as w p ( i , j ) where w p ( i , j ) is the representative for each patches share in the ( i , j ) location for reconstructing the input image located in the same mentioned location.

Each mentioned weight in its ( i , j ) location was considered in a way that the sum of the total weights will become unit. Suppose that Y is the image which will be super resolved and consider Y as patches in the form of { y ^m ( i , j ) } N ₌,. For the images in the learning database, the images available at the location ( i , j ) like X^pM ( i , j ), will be a placed patch for the image patch of Y^M ( i , j ). We expect that each patch like Y^M ( i , j ) in the human face image of { y ^m ( i , j ) } N ₌₁ to be expressed as (1).

P

YM (i, j )=Z *. (i, j )XpM (i, j) + e (1) p=1

where e remarks the reconstruction error. From (1) we can realize that the optimum weights for reconstructing the image depends on minimizing the quantity of the error e .

P ²

w ^ i , ^j ) = argmin Y M ^{( i} , j ) - £ w m ^{( i} , j ) X^P M ^{( i} , j ) w p ( ⁱ , j )                       p = 1

where w ( i , j ) is a P dimensional weight vector for each reconstruction weight of w p ( i , j ). For each value of p =1,2,..., P the value of U can be calculated by (3).

U = Y M ( i , j ) A T - X                           (3)

where A is a column vector of ones and U is matrix which its columns are the values of the X^pM ( i , j ) patches. The local matrix of V can be found by V = U ^T U . Equation (2) is a constrained least squares problem where its solution can be as:

w ( i , j ) = ( v -¹ A )/( A^TV -¹ A )                           (4)

A better way in obtaining w ( i , j ) is solving the linear system V . w ( i , j ) = A followed by changing the scales in order to a sum of one in the patches weights. w ( i , j ) can be used to reconstruct the new image patch Y M ( i , j ) from (5) as:

P

Y M ( i , j ) = Z W p ( i , j X M ( i , j ) = Y M ( i , j )          (5)

p = 1

where Y M ( i , j ) is a vector converted into a matrix used to construct the whole image. The whole image is constructed by integrating the patches considering their original locations. The values of the overlapping pixels are calculated by averaging the pixel values between the two overlapping neighbor patches.

• C.    Super Resolving based on patches

While having the LR image Y_L and the HR pair of this image Y_H which is q ² times bigger, the image resampling can be expressed by [3]:

• 1    q ^{- 1} q ^{- 1}

^y l = —EE ^y h ⁽ qⁱ + k , qj + l ⁾⁺ n ( ⁱ , ^j )           ⁽⁶⁾

q k = 0 i = 0

where q is a positive number and n ( i , j ) represents a random noise. If Y_p , Y H and n are vectors as L x 1, K x 1 and K x 1 respectively, (6) can be simplified to:

Y l = HY_H + n                              (7)

where H is a K x L matrix. Equation (7) includes a smoothing and down-sampling process which can be expressed as (8) in image patches.

{ Y LM ( i , j ) } M = 1 = H { Y M ( i , j ) } M = 1 + n                   (8)

For each Y^M ( i , j ) patch in the LR input image the weight of w p ( i , j ) is obtained from (1) to (4) and satisfies (9):

P

Y M (i , j ) = E X^PpM ( i , j ) W p ( i , j )                     (9)

p = 1

Replacing each LR image patch X ^pM ( i , j ) with its proportional HR one X ^pM ( i , j ) results in (10).

P

E X^ppM ( i , j ) W p ( i , j ) = Y p ^p M ( i , j )                    (10)

p = 1

Without considering the effect of noise from (7) and (10) we have:

P

H .Y H ^M ( i , j ) = E H . X H ^M ( i , j ) W p ( i , j ) p = 1

P

= E X^ppM ( i , j ) W p ( i , j )

p = 1

From (9) and (11) we have:

Y p ^M ( i , j ) = H Y HM ( i , j )

It can be seen from (12) that the degradation value of Y^M ( i , j ) is close to the LR input Y^M ( i , j ) . All the HR patches Y^M ( i , j ) , are integrated to reconstruct the HR whole final output image { Y M ( i , j ) } " _{= t} considering their original locations. The values of the HR pixels which are in the overlapping regions are calculated by averaging the pixel values between the two overlapping HR neighbor patches.

The symbolic super resolving process shown in Fig. 3 can be described in these steps. At the first step the input image will be reshaped into patches as described before. In the next step each LR patch is compared to the proportional LR patches in the learning database according to their location and receives one weight by each comparison. In the third step the concluded weights created by comparing the LR images are used as weights proportionally on the HR pairs and at the end the HR output is created by integrating the HR output images created in the third step.

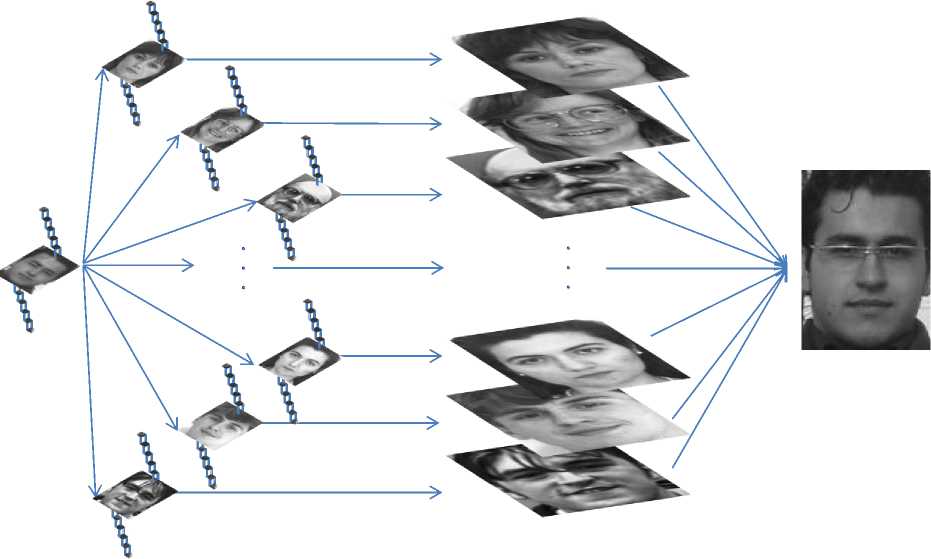
Fig. 3 The framework of using high and low resolution image pairs in the proposed face hallucination method

• D.    T HE LEARNING D ATABASE

In order to create the learning image database 600 frontal face images were used. These images were brought from famous available image databases such as ORL, ESSEX, YALE, ABERDEEN and LFW. Using multiple databases increases the functionality and makes the system robust. Although different available races, illuminations, facial poses and other conditions that has effects on the image reconstruction are gathered together in the face database, the proposed system functions hale.

The database images were all firstly converted to gray-scale. In order to create the high-LR image pairs from the available databases at first the images which the region containing the face had a resolution higher than 96 × 128 pixels were selected. After the face region was centered and replaced in a 96 × 128 window in such a way that the center of the two eyes and the ending point of the noise followed a pre marked face image used as a reference it was cropped. Following this operation the LR image pair was created by having a 4x size reduction which was handled by smoothing and down-sampling the HR pair ending in a 24×32 pixels facial image. The mentioned window sizes are determined to 96×128 and 24×32 pixels because most automated face processing tasks are possible with 96×128 pixel images [3].

We developed a resolution enhancement in a 24×32 pixels facial image. The mentioned window sizes are determined to 96×128 and 24×32 pixels because most automated face processing tasks are possible with 96×128 pixel images [3]. We developed a resolution enhancement algorithm, specifically for faces, that can convert a small number 24×32 pixel image of a face into a single 96×128 pixel image. It shall be mentioned using this method we can still have an increase in resolution from a desired input image size to a desired output by changing the database image pairs but based on the image pair sizes the quality of super resolving may vary to a higher or lower facial image output.

• IV.    Evaluation

In order to quantifiably measure the performance of the proposed algorithm, we evaluated the peak signal-to-noise ratio (PSNR) and the Structural SIMilarity (SSIM) index [15] as measurements between the ground truths face images and the hallucinated facial images. The Mean Square Error (MSE) and the PSNR are the two error metrics used to compare image compression quality which have clear physical meanings and are simple to compute. The MSE represents the cumulative squared error between the compressed and the original image, whereas PSNR represents a measure of the peak error. The lower the value of MSE means the lower the error. Again, the higher the PSNR also means the better the quality of the compressed or reconstructed image. However, they are not very well matched to perceived visual quality. To compute the PSNR, at first the mean-squared error is calculated using (13):

∑ [ I ₁( m , n ) - I ₂( m , n )²]²

MSE = M,N (13) M∗N where M and N are the number of rows and columns in the input images, respectively. Followed by (13) PSNR is computed using (14):

PSNR = 1010g. JI (14) ¹⁰ ( MSE )

where L is the maximum fluctuation in the input image data type. Since the facial images are gray-scale 8-bit unsigned integer data type, L is 255.

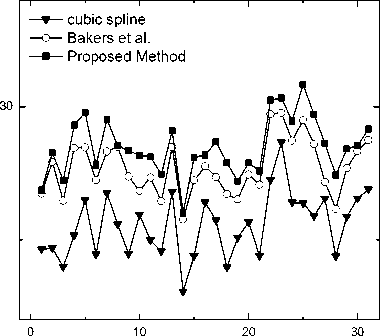
The MSE/PSNR is not as consistent as the human eyes perception in measuring the visual quality of images; hence the SSIM as a complementary measurement to evaluate the respective methods performances is also adopted. SSIM is a method that provides a quality measurement of images based on their structural contents. Since the structures of the objects in the scene are independent of the illumination, SSIM separates the influence of the illumination. As SSIM is based on structural content rather than Mean Squared Error with error weighted by different visibility models of the human visual system, it does not suffer from this issue, yet is strongly correlated with perceptual image quality. For SSIM, the highest score happens when two images are identical. The PSNR and the SSIM values for a sample of randomly selected individuals are plotted in Fig. 6 and Fig. 7 respectively. Fig. 6 and 7 shows that our proposed method has better score than that of the other two techniques in terms of PSNR and SSIM, which were confirmed also by the visualization of Fig. 4

(e)             (d)            (c)              (b)            (a)             (e)             (d)              (c)             (b)            (a)

Fig. 4. Comparing the proposed method a)low resolution facial image b)cubic spline c)Baker’s method d)proposed method e)original HR image

Fig. 5 A real world image of Irans soccer team 2010 with the hallucinated facial images based on the proposed method

PSNR

Index of Test Individuals

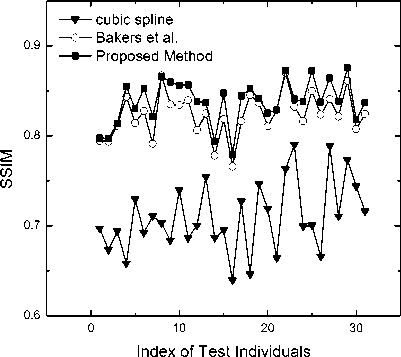
Fig. 7 SSIM values of the hallucinated results of three different methods of 31 randomly selected individuals

Fig.

. 6 PSNR values of the hallucinated results of three different methods of 31 randomly selected individuals

• V.    Experimental Results

In order to show the improvement of the images resolution and having an easier comparison, the results of implying the described method is brought in Fig. 4. At first the LR input image with the size of 24 × 32 pixels is shown the result of face hallucinating using cubic spline and Bakers [3] method is brought next and finally the mentioned method and the original HR image is brought in the last two columns. A real world image is brought in Fig. 5 including the LR images used as inputs and the hallucinated HR outputs. In order to quantifiably measure the performance of the proposed algorithm, we evaluated the peak signal-to-noise ratio (PSNR) and the Structural SIMilarity (SSIM) index as measurements between the ground truth face images and the hallucinated facial images brought in Fig. 6 and 7. Comparing Fig. 4, 6 and 7, our proposed method has better score than the other two techniques in terms of PSNR and SSIM and also by the means of human visualization.

• VI.    Conclusion

A practical facial super resolution method based on the acquired weights form image patch pairs was described in this paper. High and low resolution image pairs in the image database were the key for in the learning stage. A patch was removed from a defined location of the LR input image and was compared with the LR training images patches with the same location. By this comparison a weight for each LR images patch is gained. After estimating the corresponding weights, the learning databases HR images patch which was a pair for the LR images patch was used to hallucinate the input LR image. The HR output image was constructed by integrating the HR hallucinated patches. Experimental results demonstrate performance superiority and novelty in terms single modal face hallucination.