Фактор пространственной конфигурации молекулярного иона D~ в спектрах примесного поглощения квазинульмерной структуры

В последние годы развитие полупроводниковой наноэлектроники имеет устойчивую тенденцию к дальнейшей миниатюризации, где ключевую роль начинают играть молекулярные состояния. Такие состояния, полученные в квантовых точках, например, с помощью технологии 5-легирования [2], являются удобными объектами для исследования их электронных и оптических свойств. Действительно, квантовая точка в этом случае интегрирует в себе как атомные, так и молекулярные процессы, которые могут быть использованы при разработке кубитов, а также фотоприемников с широкой полосой чувствительности. Ввиду размерного ограничения важную роль начинает играть вид пространственного расположения атомов, формирующих молекулу в квантовой точке. Цель данной работы состоит в теоретическом изучении влияния вида пространственной конфигурации трехатомного молекулярного иона на термы и оптические свойства структур с квантовыми точками.

Термы молекулярного иона D? Рассматривается полупроводниковая сферическая квантовая точка (КТ) радиусом /?0. Последующие вычисления проводятся в сферической си стеме координат с началом в центре КТ. Для описания одноэлектронных состояний в КТ используется потенциал конфайнмента в виде ос-цилляторной сферической ямы:

*22

/ \ Ш Ы.. Гv»V)=—^—’   0)

где т*— эффективная масса электрона; й)₀— характерная частота удерживающего потенциала КТ г < R_y

В приближении эффективной массы гамильтониан в выбранной модели определяется сле дующим выражением:

А² Г 1 d Г 2 Я = ~^~Г — — г 2т I г² dr!

• ^{1    3} f ³ ) --sin 6 — + —г sin0 d^ dd| г²

  d

  

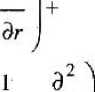
  sin0 9ф

  
  

^т г 2

-у "о7

Собственные значения Д_пт,и соответствующие волновые функции W _t гамильтониана имеют вид:

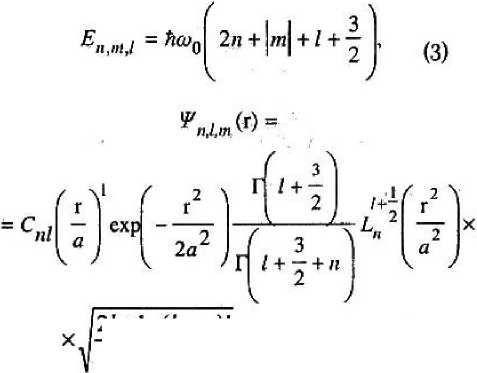
—. IL_^/j“ (cos о)еХр [гт(р] (4) 4л (/ + №)! ' J

Здесь С „, = ^nirO + п + 3/2>³/Г(1 + 3/2) — множитель нормировки; Ь^Чг²/аЧ — обобщенные полиномы Лагерра; P_t (cos 0) — присо-. единенные функции Лежандра первого рода; л, /и гп — рздиальное, орбитальное и магнит- ■ ное квантовые числа соответственно; г, 0, ф— сферические координаты.

Трехцентровой потенциал, моделируется суперпозицией потенциалов нулевого радиуса мощностью у=2р/г/(aim*), / = 1,2, который в сферической системе координат определяется как

V₅ = X у, 5 (г - Л;)[1 + (г - R_j )V_r L (5)

Уравнение Липпмана — Швингера для связанного состояния запишется в виде

^^^1-^2.^) = cJ^Gtr, г,; Еа)У<5(г1; Z?ap R^’ Аз^х (6)

Х^ Аг А2' Аз>-

После подстановки (5) в (6) получим (7)

(/iaii l^y + y2til2c2 + y3al3c3 О,

• ⁴    Y1^Q2\^CV "^ (У2°22 ^— ^2 "*" Уз^гЗ^З ^— ^’   ^^

  /^3 А + У2^32^с2 + (Уз^зз ' ^3 = ⁰’

здесь q =Й^)Й.^гД); ^ = с3 = (f3A)(Mi A); ^(f^XrR'AY

В случае, когда у, = у₂ = у₃ = у , из (9) получим

I                                       1

— - (а_п + а₂₂ + й_3э) ^₂ -

(°23й32 +a12c21 +о13е31 *°22a33 "allc22 “

" °11^й33^ У ~ ' \^11^22^33 "^ ^а12^а23^а31 ⁺ (Ю)

+ tii3a21ti32 ” ®i3^22^31 ~~

"^11^23^32 ^а12а21й3з)~ О

Рассматривая уравнение (10) как алгебраическое уравнение третьей степени относительно 1 /у, путем подстановки 1 / у = у + (a_N + о^ + д₃₃) /3 можно привести его к «неполному» виду: у³ + + ру + q, где коэффициенты р и q даются выражениями вида

Р = -(в,, + а,₂ + о₃₃)7з -(д^ + а^ +

+ ^13^31 ~ ^22^33 —aH^Z! " й|1а3з)

у — — 2(а, _£ + д₂₂ + а_и ) /27 - (й,, + й_н + с_эз Х^йи^йзг⁺

^{+ а}12^а21 +^ai3^fl3l ^^ti22^a33"^titl^fl22 ^-£111^а3з)/^"

~(^Па12аМ +а12а2?й31 +ai)a2lti31 ~а1Эа12а31 ”

I ~ ^Й11°2з4з2 ** 0|2^СИ^аЗз)

^(г, (р, е, ф ,фр е_р г₂,ф₂,9₂, Г_э, ^₃, 9₃) = Y;G(r, Ф, 9, Г_А ,фр Ур £_д) х ^x(№X^i ,

P9_v; г^ф^в^ г_г,ф₂,е_г,

г₃,^₃,0₃) +                    (?)

+ y₂G(r, Ф, 9,г₂,ф₂, е₂, ^ХГ]^)^, ф₂, е₂; г_гф_р в_рг₂,ф₂,6₂, г₃,ф₃, 0₃) +

+ y₃G(r, ф, 9, Г₃, фр 0_Э, Е_х^Т^х^^гЗ' ^3’ ⁹3 ifp Ррбр Г₂, Ф₂, е₂, г_э,ф₃,0₃),

ГДе f =lim[l + (F-R.^J

Действуя оператором Tj на обе части соот ношения (7), получим систему алгебраических уравнений вида:

ственно в виде равнобедренного н

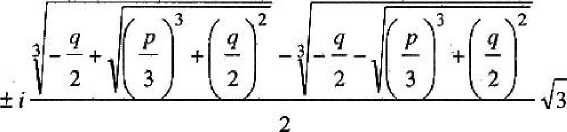
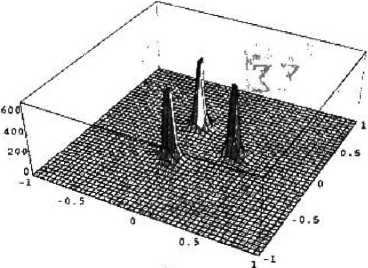
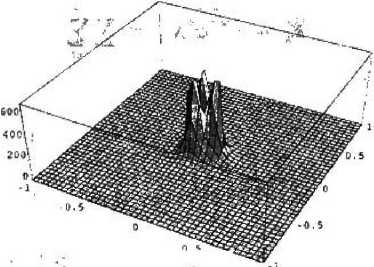
На рис. 1 представлена зависимость термов молекулярного иона D^ от вида его простран- зависит

ственной конфигурации в КТ. Как видно из рис. 1, энергия связи электрона [fj от вида пространственной конфигурации примесной молекулы в КТ, при этом меняется и величина расщепления между g- и и-термами. Рис, I, d и рис. 1, б соответствуют случаю расположения D -центров в КТ-центрах соответ- равносто- роннего треугольников. Видно, что в случае равностороннего треугольника антисимметричные ЙЕ - И 11 -ТРПМЫ ЙЫПОЖПеИЬТ R ОПИИ ЯнТИГИММАТ-- - |    - ~ ~   Г Г~1  '— ГГ1 т ■ ' 1-1 ■ ■ ■ * ■ w ■■ ■ ричный у-терм. В случае расположения D -центров в виде регулярной цепочки симметрии" но относительно центра КТ вырождение между#- и м-термами снимается (см. рис. 1,з), что связано с преимущественной локализацией электрона на центрированном доноре.

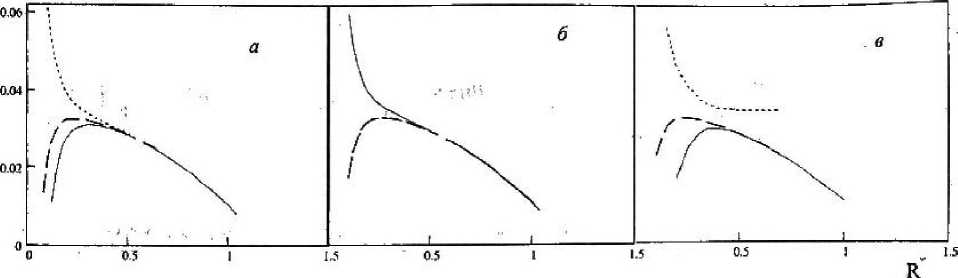
Рисунок. /

Зависимость энергии связи |е$ | электрона от расстояния между В_а-центрами, при Е. = 0,0035 эВ; R_g = !95нм; U_o = 0,1 эВ; а—расположение Dg-центров в виде равнобедренного треугольника; б — расположение О_в-центров в виде равностороннего треугольника; в — расположение D^-центров в виде регулярной цепочки симметрично относительно центра КТ

Оптические свойства квазинульмерных молекулярных состояний. Рассмотрим примесное поглощение света структурой, представляющей собой прозрачную диэлектрическую матрицу с синтезированными в ней КТ. Предполагается, что в каждой КТ содержится D^ -центр.

Эффективный гамильтониан взаимодействия с полем световой волны с единичным вектором поляризации е^ и волновым вектором у определяется выражением

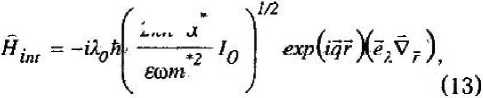
где А_о — коэффициент локального поля; /₀ — интенсивность света; w — его частота; е — статическая диэлектрическая проницаемость; а' — постоянная тонкой структуры, с учетом г диэлектрической проницаемости материала КТ.

Пусть £)°-центры локализованы в точках

R₁ = (/?,я/2,о) R₂ =(0,0,0) R₃ ^R^ju^ (см. вставку на рис. 2) и ^ = (я,л/2,о) ^=^^12^(2^ R₃ Цкл/г^!), (см. вставку на рис. 2,6). В этом случае волновая функция ^^(г, <р,9; Г] ^,5,; г,,<р_г,8₂; г₅,<р₃ ,У₃)

0;Я„ —

2yrR

а:(1-Г) (1-у")а:

sin

2а2(1-у2) (1-г)а

^(l+y²) 2yrR

2а2 (1-у2) (1-у2)а2

2а2 (1-/) (l-y-)a’

Я²(Иу^а) lyrR

2а3(1-у3) (1-/)а

связанного электрона, при выбранном расположении О°-центров, определяется соответственно выражениями вида

где нормировочные множители С, и С2 определяются как             '

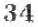
y^"¹! г,ф,9;кД,0;0,0,0;К, — Л

I 2          '           2

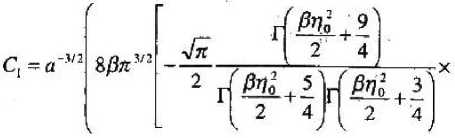
Окончательно выражения для коэффициентов поглощения K^eh и КАаА рассматриваемой структуры с КТ можно представить в виде:

M^QO.X

т л!(2^ + 1)ЙГ(2й+7+^

Г(/ + л + -)(Г^)

^Дг^, е) fo.,, ^ч*^ фал^Л^^м^

^l^.^E^ ®                   (18)

Матричные элементы ^ удД, определяющие величину силы осциллятора дипольных оптических переходов электрона из D₃ -состояния ^^D) (г,<р,5; г;,^, 9_t; г₂,<9, ,6₂; г₃,Рз, 6J центра в состояния Ч^, _f(r,

j света (вектор поляризации направлен вдоль оси г прямоугольной системы координат), запишутся следующим образом:

Г(/ + л + ^-77о)3

где /V = MJ — целая часть выражения A = f|^(x-^)~2,,~TAl = MJ — целая часть выражения Аг = ^Д (^“А?)-^; коэффициенты ^ и с2определяются системой (9); Р(и) — функция ралсределения радиуса КТ Лифшица — Слезова [2].

	З4ей1 ехр[-1/(1 - 2и 13)]	м<3/2	(21)
к»У	^Чз+иТЧ^-иГ'
	0,	к>3/2

При этом правила отбора таковы, что оптические пререходы из g-состояния р;-центра оказываются возможными лишь в состояния КТ с магнитным числом m ^ 0 и нечетным значением орбитального квантового числа I = 2nl+I.

КДш), см"                        КЦш), см'1

Рисунок. 2 Спектральная зависимость коэффициента примесного поглощения при фотоионизации Dy -центров в квазинульмерной структуре; U_Q = 0,1 эВ, R_fl = 65 нм, для различных значений R_a; f-R_e = 20нм, 2 - R_a = 13нм (а — пространственная конфигурация Dy -центров в виде равнобедренного треугольника, б — пространственная конфигурация в виде регулярной цепочки)

На рис. 2 представлены спектральные зависимости коэффициента примесного поглощения с учетом различной пространственной конфигурации Р0-центров в КТ. Можно видеть, что переход от пространственной конфигурации Ро-центров в виде регулярной цепочки(см. рис. 2, а) к конфигурации в виде равнобедренного треугольника (см. рис. 2, 6) сопровожда- ется значительным уменьшением (примерно на порядок) величины коэффициента поглощения, что связано с существенным влиянием границ системы. Действительно, если в первом случае электронная волновая функция локализована в основном в центре КТ, то во втором случае электронные состояния с равной вероятностью распределены на трех £>0-центрах, расположенных вблизи границ КТ. Следует отметить, что уменьшение расстояния R между ^-центрами приводит к усилению интерференционных эффектов. Это видно из рис. 3, где представлена зависимость квадрата модуля волновой функции-состояния от расстояния между Ь0-центрами, в случае их расположения в вершинах равностороннего треугольника (см. рис 3, а,б).

Таким образом, в работе показано существен-рнгиитяр ДИЛЯ ПППСТП.уиг,,гприилй KHurhurv-ЛСУСг U^l СДД М Ж 11- ипДы Jlpw t     I, 1    •»! Vil livti^uiij рации D*-центра в KT на g- и u-термы и оптические свойства квазинульмерных структур Р”-центрами. Это важно для интегрирования в КТ атомных и молекулярных свойств, которые могут быть использованы при разработке кубитов и фотоприемников с достаточно широкой полосой чувствительности.

а

в

Рисунок 3

Эволюция квадрата модуля волновой функции электрона |’?А|' локализованного на Dj -центре, в зависимости от расстояния между О0-центрами: а — R*0 = 1, R* = 0,3, б - R*0 = 1, R« = 0,1

БИБИДИОГРАФИЧЕСКИЙ СПИСОК

• 1.    Лифшиц И. М. О кинетике диффузионного распада пересыщенных твердых растворов / И. М. Лифшиц, В. В. Следов // ЖЭТФ. 1958. Т. 35, вып. 2(8). С. 479 — 492.

• 2.    Шик А. Я. Полупроводниковые структуры с д-слоями (обзор) / А. Я. Шик // ФТП. 1992. Т. 26. № 7. С 1 161 — 1 181.

Поступила 14.03.07.

УСИЛЕНИЕ МИКРОВОЛНОВОГО ПОЛЯВ ПОЛУПРОВОДНИКОВЫХ СВЕРХРЕШЕТКАХ*

Н. Н. Хвастунов,

Полупроводниковые сверхрешетки привлекают к себе большое внимание благодаря потенциальной возможности использования их в качестве генератора и детектора терагерцевого электромагнитного излучения (0,3— 10 ТГц) [8; 11]. Необходимость в таких устройствах вызвана быстрым прогрессом терагерцевой науки и технологии в различных областях знаний [5]. Классические работы [2; 4] стимулировали большую теоретическую активность, посвященную нелинейному взаимодействию высокочастотного электрического поля с минизонными электронами СР. В этих работах было показано, что нелинейные свойства СР дайт возможность генерации ТГц-излучения в области отрицательной дифференциальной проводимости (ОДП). Одним из наиболее интересных предложений было использовать частотное умножение для генерации высокочастотного излучения [3; 7]. В то же время система является нестабильной к формированию высоко- и низкочастотных доменов в этом режиме [1]. В результате домены могут сильно подавить усиление на ТГц-ча-стотах или сильно уменьшить эффективность усиления в сравнении с предсказаниями теории.

Следовательно, необходимо так модифицировать классическую схему блоковского осциллятора, чтобы избежать возникновения доменов

' Работа поддержана грантом Президента России для молодых кандидатов нарк (МК-4804.2006.2)

(или подавить уже появившиеся электрические домены), но при этом сохранить усиление. Чтобы избежать эффектов, связанных с ОДП-не-стабильностями, мы предлагаем использовать переменное поле накачки вместо приложенной постоянной, разности потенциалов и рассматривать усиление на гармониках накачки. Сильное переменное поле в этом случае при определенных условиях подавляет нестабильности волн пространственного заряда (ВПЗ) внутри сверхрешетки и в тоже время является источником энергии для генерации и усиления гармоник. Детальный анализ этой схемы дан в [10], где было показано, что квазистатическое поле накачки может полностью подавить домены в СР.

Однако домены могут возникать в СР и в чисто переменном поле в динамическом случае благодаря нестабильности системы к малым флуктуациям постоянного поля. Причина этого лежит в создании горячих электронов с отрицательной эффективной электронной массой. В нашем случае необходимое условие формирования доменов в СР такое же, как и условие абсолютной отрицательной проводимости (ДОП) с произвольно малой приложенной разностью потенциалов. В этом случае регионы усиления шире, чем регионы ОДП, и мы можем использовать эту схему блоковского осциллятора для усиления ТГц-излучения. Интерес к данной теме возрос благодаря недавним экс-