Факторная оптимизация энергетических параметров гидромашины

В данном исследовании решение задачи оптимизации энергетических параметров гидромашины было реализовано на примере малоразмерного центробежного насоса (ЦН). В качестве критериев эксплуатационной эффективности работы рассмотрены значения энергетических параметров, используемых при проектировании проточной части в качестве целевых функций. В качестве факторов рассматривались абсолютные и относительные геометрические размеры проточной части гидромашины. Целью факторной оптимизации стало получение полиномиальных регрессионных однофакторных математических моделей, используемых в методике проектирования проточной части. Структура поиска оптимальных проектных решений в данном исследовании имела схему, представленную на рис.1.

При гидравлических испытаниях опытной ступени насоса с различными вариантами закрытых рабочих колес (РК) в качестве контролируемых параметров исследовались энергетические показатели – напор и КПД, замеряемые в процессе испытаний при заданной величине числа оборотов и изменении расхода рабочего тела [1]. В качестве факторов рассматривались безразмерные геометрические соотношения проточной формы: D 1 , b 2 /D 2 , F, b 2 /L [2, 3].

Рис.1 . Структура поиска оптимальных решений

В таблице 1 представлен состав факторов, а также безразмерных целевых функций корреляционно-регрессионного анализа, связанных с контролируемыми параметрами насоса. Физическими объектами экспериментального исследования стали рабочие колеса (рис. 2),

Каталажнова Ирина Николаевна, кандидат технических наук, доцент кафедры высшей математики геометрические соотношения проточной формы которых зависели от следующих конструктивных размеров: D2 – наружный диаметр колеса; b2 – ширина лопаток в выходном сечении; β2л – угол лопатки на выходе; D0 – диаметр входа в насос; D1 – диаметр входа в РК; β1л – угол лопатки на входе в колесо; z – число лопаток колеса; Т1 и Т2 - соответственно коэффициенты стеснения потока лопатками на входе и выходе из колеса.

Таблица 1. Состав целевых функций и факторов

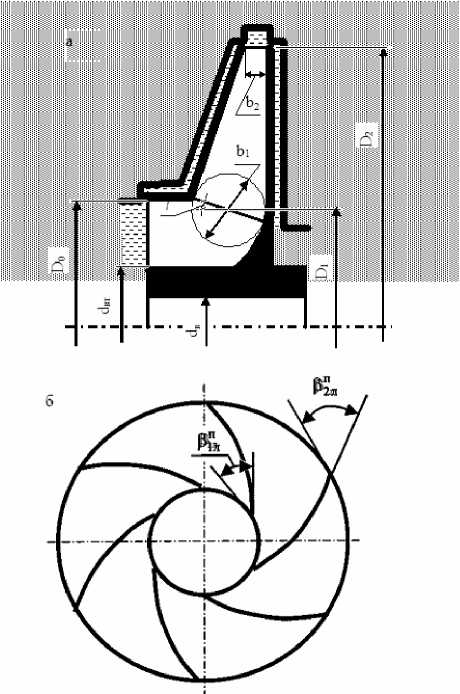
Рис. 2. Геометрические размеры РК: а – меридиональное сечение; б – окружное сечение

На рис. 3 и рис. 4 представлена взаимосвязь геометрических размеров каналов РК, позволяющая проанализировать схему изменения проточной формы каналов при подрезке лопаток РК или изменении угла. Варьирование углом р2л, его уменьшением с 90° до 30°, обеспечивает увеличение относительной длины межлопаточных каналов L, см. рис. 4, где L = L/L       . Для всех колес использовалось р2л=90о постоянное отводящее устройство в виде спирального сборника с шириной b3=4,4-10-3 м. Спиральный сборник переходил в прямоосный диффузор. Перед каждым испытанием контролировалось постоянство осевого зазора (5=0,5^10-3, м) между колесом и корпусом насоса.

р2лг град

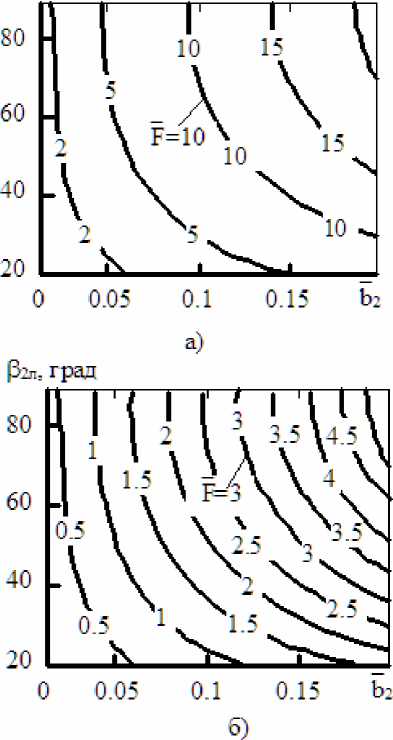
Рис. 3 . Зависимость степени диффузорности каналов F от независимых факторов b₂ и р _2л: а - D i =0,25; б - D 1 =0,8

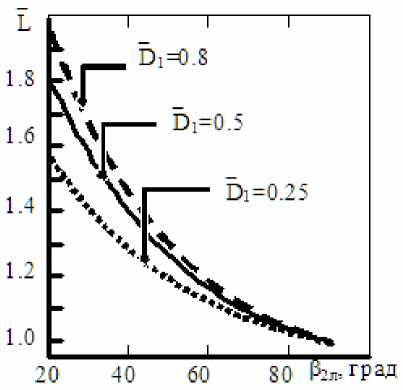
Рис. 4 . Взаимосвязь геометрических факторов РК ЦН

Испытания ЦН на воде с температурой T=20-22 ° C проводились на стенде с замкнутым контуром. Результаты испытаний в виде напорной и КПД-характеристик подвергались обработке с целью определения точки расчётного режима, характеризуемого максимальным значением полного КПД насоса. Пример энергетических характеристик ЦН, найденных экспериментальным путем, представлен на рис. 5.

Математическое моделирование влияния геометрических и режимных параметров на энергетические показатели ЦН проводилось согласно схеме, при которой результаты гидравлических испытаний ЦН подвергались кор-реляционно-регресионному анализу. Факторы, оказывающие наиболее существенное влияние на функцию отклика, включались в регрессионные математические модели, связывающие гидродинамические параметры с геометрическими размерами проточной части и режимами работы. Корреляционный и регрессионный анализ экспериментальных данных проводился на основе типовых алгоритмов [6-8]. В таблице 2 представлен фрагмент результатов анализа однофакторных моделей энергетических параметров ЦН, зависящих от диаметра D1 (при β2л=const), которые в дальнейшем были использованы для проектирования проточной полости насоса.

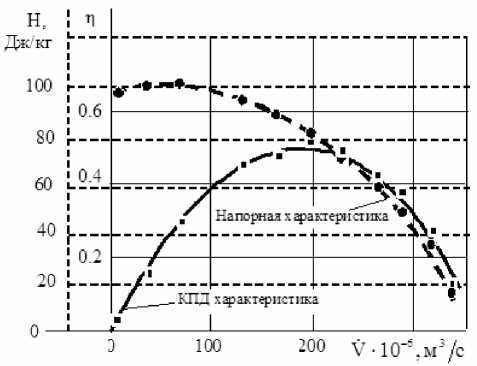
Рис. 5. Энергетические характеристики ЦН (в_2л=30°; D 1 =0,25; b₂=0,109; n=6000 об/мин)

Таблица 2 . Однофакторные математические модели энергетических параметров ЦН

Примечание: * - множественный коэффициент корреляции

Выводы: однофакторные уравнения связи между энергетическими показателями и геометрией проточной части целесообразно использовать уже на первом этапе проектирования для предварительной оценки выходных параметров гидромашины. Это позволяет существенно уменьшить число итераций расчёта на последующих стадиях проектирования.

Кроме того, наличие таких уравнений облегчает в рамках доводочных испытаний вновь создаваемых конструкций целенаправленно трансформировать проточную часть и добиваться повышения энергетической эффективности гидромашин, проводя минимальное количество гидравлических испытаний.