Fast and Efficient Design of a PCA-Based Hash Function

Published Online May 2015 in MECS

Cryptographic hash functions are important cryptographic primitives. They compute a digest of a message which is a short, fixed-length bitstring. For a particular message with an arbitrary length, the message digest, or hash value , can be seen as the fingerprint of a message, i.e., a unique representation of a message.

Unlike all other cryptographic algorithms, hash functions do not need a key in order to compute a message's hash, except some specific implementations named keyed hash functions that are used for specific signature scenarios. The use of hash functions in cryptography is manifold: Hash functions are an essential part of digital signature schemes and message authentication codes (MACs). Hash functions are also widely used for other cryptographic applications, e.g., for storing of password hashes or key derivation [1].

From a structural point of view, cryptographic hash functions may be categorized into three main classes based on the nature of the operations performed in their internal compression functions: the first class functions uses a block cipher as compression functions [2] and [3], when the second class includes hash functions based on difficult mathematical problems, such as discrete logarithm problem [4], factorization problem [5] and problem of finding cycles in expander graphs [6].

Another recently emerging class covers dedicated hash functions designed especially with speed and reliability in mind [7]. Among dedicated functions, there ones based on chaotic maps that exhibits chaotic and complex behaviors with high sensitivity to initial conditions’ variations. Examples of such maps include the logistic map proposed to build a hashing schema in [8], and the tent map used for same purposes in [9].

Cellular automata (CA) have recently also been used to design dedicated hash functions. Cellular automata are very appropriate to design hash functions with a low hardware and software complexity because of their logical operation attributes [7]. CAs also provide high level of parallelism and therefore, are able to achieve high hashing speeds [10]. The main approaches using CA to construct hash functions are discussed in detail in related works section.

In this paper, we propose a new cryptographic hash function using programmable CA conjointly with the Davies-Mayer construction [11] to define compression function, when Merkle-Damgard variant construction is adopted as a domain extension algorithm. The proposed scheme is shown experimentally to be robust against the main hashing attacks, and evaluated with respect to the strict avalanche criterion and the pseudo-randomness of the hashing output considered for large scale streams.

The remaining of the paper is organized as follows: Section 2 introduces relevant background about cryptographic hash functions, CA preliminaries and related works. Section 3 details the proposed hash function construction, when Section 4 present the performed experiments with corresponding obtained results. Finally conclusions are drawn in Section 5.

• II.    Cryptographic hash functions and cellular

AUTOMATA

In the following, we introduce the basic necessary definitions related to cryptographic hash functions and cellular automata, and then we briefly describe the main works with relevance to the construction of CA-based hash functions.

• A.    Cryptographic Hash Functions

Formally speaking, a hash function H is a deterministic and efficient algorithm that maps an arbitrary length binary message M to some fixed length (typically 128, 160, 256 or 512 bits) fingerprint h [1].

H:{0,1}^* → {0,1}ⁿ

M → h =H(M)               (1)

To be considered as cryptographic, a hash function should resist to the three main attacks: the pre-image attack, the second pre-image attack and the collision attack. The pre-image attack consists for a given hash value h to find the corresponding message M such that H(M)= h . The second pre-image attack succeed if for a given message M and a given hash value h =H(M) we can find a message M≠M' such that H(M')= h . Finally, the collision attack aim to find two arbitrary distinct messages M and M' such that H(M)=H(M').

Using a brute-force attack, pre-images and 2nd preimages attacks succeed deterministically after 2n call to the function H, when a collision is very leaky to succeed using only 2n/2 call to H according to the birthday paradox theorem. It is usually the goal in the design of a cryptographic hash functions that no attacks perform better than the brute-force attack.

In general, it is not always possible to get a formal proof of resistance to such attacks. But in contrast, some statistical properties are easily verifiable to show that a given hash function has a good cryptographic level of security. A hash function that behaves like a pseudorandom function and satisfies the avalanche effect is generally considered to be secure and can be used safely for cryptographic purposes. Such statistical properties are easy to check, and then enable a fast and acceptable evaluation tool to validate the hash functions design.

Cryptographic hash functions have generally two main independent components: the mode of operation (a domain extender algorithm) and the compression function. Most popular hash functions are based on iterating a compression function that processes a fixed number of bits. The message to be hashed is split into blocks of a certain length where the last block is possibly padded with extra bits.

Let h:{0,1}ⁿx{0,1}^L → {0,1}ⁿ denotes a compression function, where n and L are positive integers, and let M=m₀|m₁| |m_k be the message to be hashed, where |m_i|=L for 0≤ i≤ k. The hash value is then defined to be h_k, where h i =h(h i-1 ,m i ) defines the chaining variables.

A hash function can be either keyed or non-keyed one depending on the corresponding intended use. For nonkeyed functions addressed in the present work, a fixed initialization vector IV is used to define the value h 0 . If the message M to be hashed cannot be split into blocks of equal length n, (if the last block consists of less than n bits), then a collision-free padding rule should be used [12].

It has been shown that attack on a given hash function implies similar attack on the corresponding used compression function. So in order to show the hash function’s resistance to the collision, it suffices to show that the property is verified for the compression function. When iterating a compression function that provides collision resistance property we can achieve a global collision resistance, and guarantee a perfect avalanche effect satisfaction by the constructed hash function.

• B.    Cellular automata preliminaries

Cellular Automata are dynamical systems in which space and time are discrete. They consist of collections of cells organized in a grid, when each cell has a corresponding current state. The states of the cells evolve over time depending on their current states and the states of the neighboring cells, according to a local and identical interaction rule in the case of uniform CAs, or different interaction rules in the case of non-uniform CAs [13].

CA were originally used by von Neumann [14] while he was studying self-reproducing systems and then popularized by Wolfram’s substantial work in this area [15], who observed that based on simple rules, very complex behaviors can be obtained. Wolfram pioneered the investigation of CA as mathematical models for selforganizing statistical systems and suggested the use of elementary CAs, which are simple 1-dimensional linearly connected array of n cells, usually referred to a 3-neighborhood CAs. Each cell in the array takes a discrete state s equal to 0 or 1. If a configuration of the CA at a time step t is defined by the binary vector C^t, and the i^th cell’s state is denoted by (C^t) i , then the transition function f is used to determine the next state of each cell from a neighborhood’s corresponding configuration. Cell’s states are updated in parallel with respect to each other cells using the transition function in each time step. The next state of a cell a time t+1 is only influenced by its own state and the states of its left and right neighbors at time t. The configuration C^t+1 at time t+1 can be computed by:

(C^t+1) i = f ((C^t) i-1 , (C^t) i , (C^t) i+1 ) , ∀ 0 ≤ i ≤ n-1 (2)

Table. 1. Transition table of two different elementary CA transition rules (Rules 30 and 2)

Neighborhood’s configuration at time t 111 110 101 100 011 010 001 000 Value of the central cell at time t+1 (Rule 30) 0 0 0 1 1 1 1 0 Value of the central cell at time t+1 (Rule 2) 0 0 0 0 0 0 1 0 Neighborhood’s configuration at time t 111 110 101 100 011 010 001 000 where (Ct)i-1, (Ct)i and (Ct)i+1 are the states of the left neighbor, self and right neighbor of the ith cell at time t. A cellular automaton with 2 states and a neighborhood’s radius equal to 1 (3 cells) has 23=8 possible neighborhood’s configurations. If the set of all possible configurations is expressed using a truth table, the decimal equivalent of its sequence output is referred as a “Rule” [15], and by the way the transition rules length is equal 8 and a total of 28=256 CA local rules can be used. Table 1 illustrates an example of two elementary rules defined by the corresponding transition tables.

If the same rule applies to all cells in a CA, the CA is named uniform or regular CA, whereas if different rules apply to different cells, it is named a hybrid (or nonuniform) CA. A programmable CA (PCA) is a hybrid CA controlled by a number of signals such that different rules can be generated.

Cellular automata have several properties that favor their use as basis for the design of hash functions. Their chaotic, complex and unpredictable behavior of some transition rules enables their effective use to design safe and reliable hash functions. The simplicity of their implementations and their parallel nature makes them suitable as a basis for fast compression functions.

• C.    Related works

Cellular automata have been widely used recently to construct cryptographic primitives. They have been used for the construction of symmetric cryptosystems, public key cryptosystems, secret sharing schemas and hash functions. The first cryptographic application of CA was initiated by Wolfram [16] that describes a stream-based cipher using the elementary CA rule 30. The CA was used as a pseudorandom numbers generator to produce statistically good sequences used to cipher plain data by the Vernam ciphering model. CAs were also used for block-ciphers constructions using reversible and irreversible rules [17], and also to build public-key cryptosystems by exploiting two-dimensional CAs reversibility problem [18].

In [19], Damgard was the first to propose a hash function based on CAs, he used Wolfram’s pseudorandom bit generation’s scheme to design a compression function, but his proposal has been cryptanalysed by Daemen et al. in [20] who, in turn, proposed a framework of collision free hash functions based on CA, named CellHash. The same authors proposed later an improved version named SubHash in [21]. Both CellHash and SubHash are hardware-oriented so making extremely high speed possible, but unfortunately, the two schemas were cryptanalysed later in [22].

Another CA-based hash function has been proposed by Mihaljevic, et al. in [23], where they describe a family of fast dedicated one-way hash functions using linear CA over GF(q). The proposal is an extension of the bit’s oriented hashing proposed earlier in [24], enhanced by employing the approved model of iterative hash function with compression and output’s functions: the compression function is one of the Davies-Meyer types employing CA, when the output function was a key generator based on CA over GF(q). In [25] Dasgupta, et al. proposed a CA based scheme for message authentication by investigating a particular class of nongroup CA that can be employed to generate an efficient message authentication function. Two-dimensional CA was also proposed as base of construction of hash functions in [26].

More recently, Jun-Cheol proposed a one-way hash function using linear and nonlinear CAs [7]. Norziana et al. proposed an alternative hash function based on CA rules 30, 134 and Omega-Flip Network in [10], then proposed another hash function in [13] named STITCH-256 using balanced CA elementary rules like rules: 29, 39 and 27, and diffusion functions to implement the compression function.

• III.    The Proposed Hashing Scheme

In this section, we present the proposed new CA-based cryptographic hash function. The proposed function follows iterative hash model inspired from the Damgard's one presented in [19], and uses two internal functions namely: a compression function C and a transformation function C. The former employs programmable CA with 4 rules (30, 90, 105 and 150), when the later T uses an hybrid cellular automaton with rule 30 and rule 105. Both message blocks and hash value are 256 bit binary strings.

• A.    The mode of operation

In the proposed hashing scheme, we use a variation of Merkle-Damgard contraction. The proposed algorithm requires a padding function (in such a way that the length of the message becomes a multiple of 256 bit) for which the last 64 bits encode the length of the message M to be hashed. The padded message is then divided into blocks M_i (i=1...k) with |M_i|=256 bits. The algorithm requires also a fixed initialization vector: IV ∈ {0,1}²⁵⁶.

The compression function C is then iterated for k times. C takes as inputs a block message M i and a chaining variable h i-1 , to produces a 256 bit string as output. This output string is XORed with the output of a transformation function T applied to the block message M i to form the next chaining variable h i . Figure 1 illustrates a pictorial representation of the proposed hashing scheme.

• B.    The compression and transformation functions

To construct the compression function, we use an elementary programmable CA (PCA) with 4 rules, namely the rules: 30, 90, 105, 150 (As there are many literature works that studied the properties of different CA rules, we used only rules that have been proven to have good pseudo-random proprieties).

We firstly define a function F that takes as input a block message M_i and a chaining variable h_i-1, to produce an output string f on 256 bits like follows:

F:{0,1}²⁵⁶x{0,1}²⁵⁶ → {0,1}²⁵⁶

(h i-1 ,M i ) → F(h i-1 ,M i )= f i                    (2)

The function F is defined like the following: a PCA of 256 bit length is initially loaded with the message block Mi. Additional 256 bits from chaining variable are doubled to form a 512 bit string S (i.e. S = hi-1|hi-1). The bits from S are used with the number of the current iteration to control the rule configuration of the individual CA cells. Each 2 bits of S control one cell rule (the bits j and j+1 control the rule of the cell number j/2) conjointly with the remainder of the iteration number modulo 4. The control logic of the proposed PCA is described in Table 2.

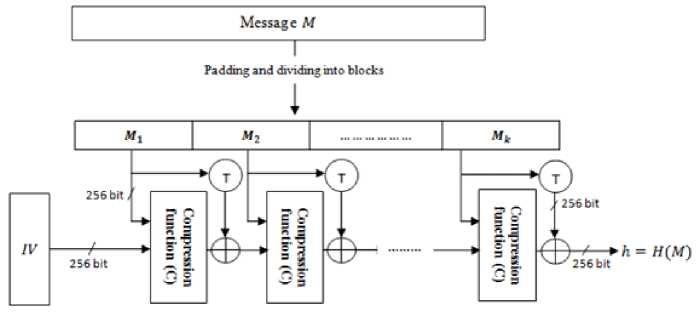
Fig. 1. Pictorial representation of the proposed scheme.

Table. 2. Control logic of the proposed PCA

2 bits from M i	i mod 4
	0	1	2	3
00	Rule 30	Rule 90	Rule 105	Rule 150
01	Rule 90	Rule 30	Rule 150	Rule 105
10	Rule 105	Rule 150	Rule 30	Rule 90
11	Rule 150	Rule 105	Rule 90	Rule 30

The CA is then iterated for n times. The value of the parameter n defining the number of iterations may be fixed according to the desired ratio of speed/reliability performances. The output of F is the defined by the final PCA state.

The compression function C is then defined using the function F as follows:

The transformation T takes as input a block message of 265 bit length and produces an output string t of 256 bit that is XORed with the compression function output. The transformation function is defined as follows: a hybrid CA with rules 30 and 105 (rules are applied in alternation i.e. 30, 105, 30….) is initially loaded with the message block M i . The CA is iterated 50 times to obtain an intermediate configuration, then iterated another 256 times to form a 256 by 256 bit square. The diagonal of this square is then taken as output of T. Figure 2 illustrates pictorial specification of the transformation T operations mechanism.

The transformation function T is used to obtain the next chaining variable hi by:

h i = c i ⊕ T(M i )

= f i ⊕ h i-1 ⊕ T(M i )

= F(h i-1 ) ⊕ h i-1 ⊕ T(M i )             (4)

C:{0,1}²⁵⁶x{0,1}²⁵⁶ → {0,1}²⁵⁶

( f i ,h i-1 ) → C( f i , h i-1 )=c i = f i ⊕ h i-1                (3)

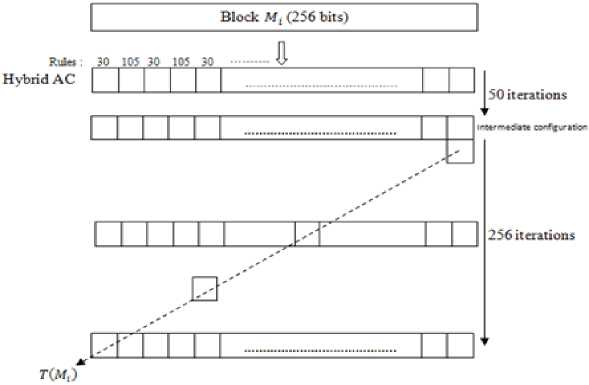
Fig. 2. Pictorial description of the transformation function T.

Using the described scheme, the proposed hash function can take any message M of arbitrary length as input, decompose it into consecutive blocs M i , and produce the corresponding hash vale H(M). The proposed function is benchmarked with respect to several performances tests with several experiments illustrated in the following section.

• IV.    Performances evaluations and obtained

RESULTS

As explained above, it is not always possible to formally proof the resistance of a given hash function to common attacks. In contrast, several statistical properties can be checked in order to show that the function provides good cryptographic level of security. Pseudorandom behavior and avalanche effect are generally considered as good security's indicators of a hash function. In this section, we perform several statistical experiments on the proposed hashing scheme. We also show that best computational performances can be achieved by the proposed scheme with respect to existing models.

• A.    The avalanche and strict avalanche criterions

Avalanche effect is a desirable property for cryptographic hash functions, that tries to reflect the idea of high-nonlinearity [27]: a little change in the input (flipping one single bit) produce a significant change of the output (approximately half of the bits are flipped).

Formally, if a function F have the avalanche effect, then the Hamming distance between its output on a random inputted binary string x and the output obtained when randomly changing one bit of x should be, on average, half of the output size [28]. This effect tries to abstract the intuitive idea of high nonlinearity: very small difference in the input must produce high changes in the output, hence an avalanche of changes.

Mathematically, F:{0,1}m→{0,1}n has the avalanche effect if it holds the following:

∀ x,y ∈ {0,1}^m: Hamming(x,y)=1

⇒ Average(Hamming(F(x),F(y)))=n/2   (5)

When Hamming(x,y) denotes the Hamming distance between the two n-bits blocks x and y. Figure 3 shows results of the avalanche effect test performed on the proposed hash function, using a set of 10000 pair of arbitrary messages Mi and Mi' such that Hamming(Mi, Mi')=1. Obtained results shows that the hamming distances between the hash values (i.e. Hamming(H(Mi),H(Mi')) are concentrated around the value 128, which indicates that the hash function has a good avalanche effect.

Another more accurate and demanding nonlinearity measurement is the so called strict avalanche criterion [29] which, in particular, implies the avalanche effect.

The Strict avalanche criterion (SAC) is a more demanding property that was originally presented as a generalization of the avalanche effect to measure the quantity of confusion and diffusion in substitution boxes (s-boxes). Formally, a function F is said to satisfy the SAC if, whenever a single input bit is flipped, each of the output bits must change with a probability of one half. This implies that the distribution of hamming distances between outputs that have similar inputs (differs in one bit) should flow a binomial distribution. Mathematically, the SAC is described by [28]:

∀ x, y ∈ {0,1}^m: Hamming(x,y)=1

⇒ Average(Hamming(F(x),F(y))) ≈ B(½,n)  (6)

Where B (½,n) denotes binomial distribution with parameters ½ and n. This definition also tries to abstract the more general concept of independence of the output from the input. An ideal hash function F will resemble a perfect random function where inputs and outputs are statistically unrelated [30].

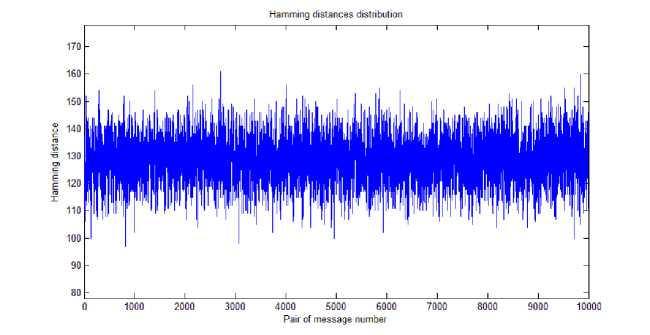
Fig. 3. Obtained distribution of Hamming distances between hashes of random messages and hashes of theirs one-bit-flipped alterations.

In order to evaluate the proposed hash function with respect to the SAC, the following experiment have been conducted: the 256 elements of an integer's vector V

(corresponding each one to a bit position of the hash function's output) are initialized firstly to 0. A set of 1000 random messages with arbitrary length are then generated, and their corresponding hash values H(M) are computed. For each one of these messages, only one bit is randomly flipped getting a new message M', that is also hashed to obtain a new hash value H(M'). The hamming distance Hamming(H(M),H(M')) is calculated, and the result is used to determine the element of V to be incremented (i.e. V[Hamming(H(M),H(M'))] ++). This operation is repeated 1000 times for each message.

Finally, the values of the vector V elements are divided by the total number of performed experiments (equal to 1000*1000=106) in order to perform a normalization of the computed distribution. The obtained values represents the distribution of hamming distances, that is compared to the binomial distribution as plotted in Figure 4.

The distance between the observed distribution of the Hamming distances and their theoretical distribution under perfect Strict Avalanche Criterion hypothesis B (1/2, n), has been also measured by means of a chi-square χ ² goodness-of-fit test [30]. The chi-square measurement is a statistical test that allows verifying the adequacy of a data set to a probability distribution by using the following formula [27]:

_χ 2 ₌ ²⁵⁵ (O i - E i ) ²

∑ i=0      Ei

when O_i denotes the observed frequency and E_i denotes the expected one. Using the distribution values obtained in the experiment described above, the value of the χ ² measurement have been computed an found to be equal to 0,005465.

Using the probability α=0.01 as our critical threshold, the hypothesis of equivalence between the two distributions is accepted if the χ2 value is less than the quantile χ255,0.01=310.45. It is clear that the obtained χ2 is negligible with respect to the quantile value, and consequently, the null hypothesis is accepted and the hamming distribution of the proposed hash function is then following a binomial distribution B(½,256).

Results of the SAC test shows that the hash function provides good avalanche effect criterion, which is one of the most important features of secure cryptographic hash functions.

• B.    Randomness statistical tests

Cryptographic primitives and especially hash functions should act like pseudorandom functions to avoid statistical attacks; therefore the output of a secure hash function must be statistically indistinguishable from the output of a random function. We performed several statistical randomness on the output of the proposed hash function in order to show that it provides best randomness properties.

In the performed experiment, the hash function has been used as a pseudo-number generator to create a data stream of 10Mb. The stream is generated using a counter mode scheme applied using the hash function on an initial random integer seed S and then calculating the values H(S),H(S+1),.....,H(S+327680) each one on 256bit. The resulting outputs are finally concatenated to form a data stream. The produced stream is analyzed statistically using both Diehard [31] and ENT [32] statistical Tests batteries, and then obtained results are averaged and reported in Tables 3 and 4. It is clear from presented results that the binary stream generated by the hash function has successfully passed all DIEHARD and ENT tests. We can conclude that the function has a good pseudo-random behavior and can as a result be considered to be statistically indistinguishable from random function.

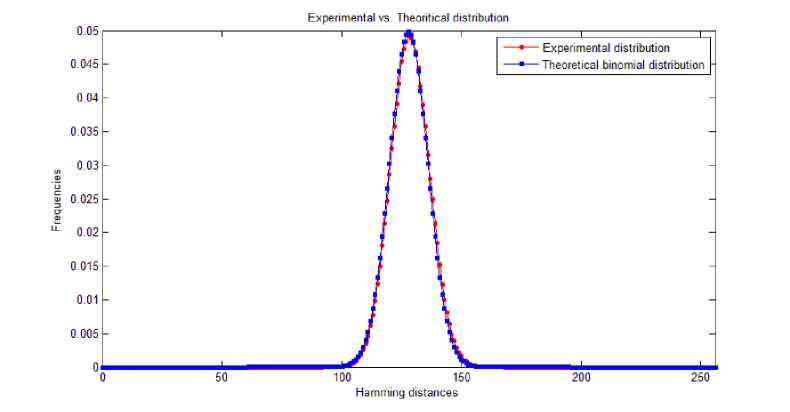
Fig. 4. Experimental hamming distances distribution vs. Theoretical binomial distribution.

• C.    Performances analysis of the designed function

Cellular automata uses simple binary operations. Therefore CA-based primitives can achieve very high speed in both hardware and software implementations. In the present work, the proposed hash function has been implemented using Microsoft Visual C++, while performance's experiments were performed using an Intel

Core i5 (2.5 GHz) microprocessor platform. Table 5 shows a comparison between the hash function and widely used ones implemented by the Crypto++ library using Microsoft Visual C++ [33]. It is clear that the designed function achieves very competitive speeds with respect to other standards, and we assume that it can achieve mush better rates if hardware implementation is used.

Table. 3. Results of the DIEHARD tests battery applied on the designed hash function’s output.

Test Name	P-value	Interpretation
Birthday Spacing	0.45155	Pass
Overlapping 5-permutation	0.65472	Pass
Rank test for 31x31 binary matrices	0.64841	Pass
Rank test for 32x32 binary matrices	0.89452	Pass
Rank test for 6x8 binary matrices	0.56274	Pass
BITSTREAM TEST	0.32912	Pass
OPSO Test	0.42485	Pass
OQSO Test	0.64271	Pass
DNA Test	0.42839	Pass
Count the 1s in a Stream of Bytes	0.69275	Pass
Count the 1s in Specific Bytes	0.39258	Pass
Parking Lot Test	0.51229	Pass
Minimum Distance Test	0.64942	Pass
Random Spheres Test	0.35862	Pass
The Squeeze Test	0.43175	Pass
Overlapping Sums Test	0.58441	Pass
Runs Up and Down Test	0.74349	Pass
The Craps Test	0. 83457	Pass

Table. 4. Results of the ENT tests battery applied on the designed hash function’s output.

Test Name	Value	Norm
Entropy	7.997982	8.0
Optimum compression	0.000003	0.0
Arithmetic mean value of data bytes	127.5586	127.5 = random
Monte Carlo value for π	3.14086552	π
Serial correlation coefficient	0.000347	totally uncorrelated

Table. 5. Speed performances comparison with respect to some known hash functions.

Hash function	Speed (MB/s)
MD5	406
SHA-1	158
SHA-256	143
SHA-512	82
RIPEMD-128	240
RIPEMD-256	195
RIPEMD-320	104
Whirlpool	80
Proposed function (256 bit)	138

• V.    Conclusions

In this paper, we propose a cryptographic hash function based on cellular automata. The proposed function uses two internals, namely: a compression function based on programmable cellular automata controlled by the chaining variable bits, and a transformation function construct from a hybrid cellular automaton with rules number 30, and 105. The proposed scheme has been experimentally analyzed with respect to several statistical test, while obtained results shows that the proposed function provides good cryptographic properties such as pseudo-random behavior and sensitivity to the input changes. In addition, the function is simple, fast, and can be easily implemented through software or hardware. Performances evaluations show that extremely optimal performances are achieved by the function with respect to existing standards, and we presume that better performances can be obtained if hardware implementation is adopted due to the inherent parallelism of cellular automata.