Fast Encryption Scheme for Secure Transmission of e-Healthcare Images

The study of image informatics was originally focused for the development of e-healthcare systems (EHSD). Observation reports, pathology reports, operation reports, imaging reports, treatment records, drug recommendation reports, information to identify patients, legal permissions, and allergies are all part of the e-healthcare systems data (EHSD). Many medical information systems in the field of medical bioinformatics currently maintain this data in a number of registered formats. The EHSDs are kept in unstructured formats, such as digitized hard copies in a standard document management system, posing a serious interoperability issue in the healthcare medical imaging area. If the EHSDs are made interoperable, it will be easier to retrieve and process clinical information on a patient from different sites, resulting in more effective and efficient patient care. The automated communication of patient data between healthcare centers will speed up delivery and reduce the number of duplicate tests. Newly discovered risks depict threats that breach the data communication event in IoT devices, indicating a risk of secure communication in the future. As a result, configuring traffic analyzers and receptors to keep track of potential threats and underpin a robust security framework is highly difficult. In this subject, empirical research advocates for the availability of lightweight encryption techniques that ensure secure data exchange. IoT platforms, according to cyber security experts, need to be highly scalable to manage billions of cyber security issues [1].

Regarding medical images transmission, some of the important challenges associated are safety, privacy, and protection. As a result, cryptographic sys- tems are becoming more important in protecting data and preventing it from being intercepted during transmission. The majority of medical health-care data is stored in the cloud. To protect medical health care images information, cryptographic mechanisms such as image encryption are required. Simultaneously, the encryption algorithms utilized must take minimal processing time, be very sensitive to the nature of the data, and be loss-less in nature [2] .

Lightweight approach based on the concept of cellular automata (CA) has been proposed by Roy et al. [3] to construct a unique encryption technique for IoT. The restrictions of IoT nodes distributed over the perception layer were addressed with this strategy. The encryption procedure is designed for the IoT Perception layer. The CA is appropriate for synthesis-required sys- tems, and its output may contain redundant data. It can be difficult to obtain a flawless rule for managing the evolution of the CA system at times. The PI is converted into 2D bit plain and m by Zhang et al. [4] . A piecewise linear chaotic map (PWLCM)-based encryption method was invented by Ali et al.

• [5]    using a permutation table and substitution s-box. A chaotic logistic map employing another key is used to construct a pseudo random number sequence (PRNS) of the size of plain image (PI). Finally, the PRNS and the image are XORed together. Mondal et al. [6] proposed a wavelet and chaos-based images encryption technique. Chai et al. [7] developed an image encryption strat- egy that encompasses the architecture of permutation using the latin square approach and integrates the latin square and chaotic systems. They used a bi-directional adaptive diffusion technique to diffuse a slight shift across the entire pixels of the image. The chaos in the proposed system is induced via a fourdimensional memristive chaotic system.

For initiating diffusion operations on coloured images, Hosny et al. [8] created a 2D LSCM. To create the ciphertext image, the image is first scrambled. After that, the chaotic system is integrated using the fractional multichannel Gegenbauer moment [8] . The algorithm has powerful encryption capabilities and a sizable key space.

Even though the proposed algorithm’s encryption efficiency is low, it is still possible to acquire the decrypted image by adding 0.01 noise. On fusing the Zigzag map, Bernoulli shift map and DNA coding, Dagadu et al. [9] built an encryption method for medical image encryption. The described encryp- tion technique distributes DNA via key generation based on chaos theory. By mixing input ASCII texts, initial process variables are produced, which are subsequently used to construct control parameters. An enhanced Arnold ping system with a mash operation to confuse and muddle the image is presented by Mansouri and Wang in their paper [10] . The algorithm can only endure security breaches while having a straightforward structure and excellent sensitivity. After several repetitive execution cycles, the security must be verified.

Talhaoui et al. [13] combined the key stream produced by this system with the permutation-less framework to disseminate and encrypt the pixel of the columns and rows of the image matrix to produce enciphered image. The proposed algorithm’s encryption speed is relatively slow. The algorithm, however, merely performs the diffusion operation, and its security require action. A novel method for encrypting medical images was addressed by Xue et al. [14] using DNA dynamic coding and the fostering of dynamic DNA chain operations in row and column chaining. The recommended method defies conventional cryptographic assaults, noise, and occlusion.

A new image encryption scheme was presented by Stalin S. et.al [15] by fusing the capabilities of block-wise encryption, 4D logistic maps, and DNA systems. Pixel replacements are built using a nonlinear 4D logistic map, and each block is effectively encrypted using DNA coding. The test results indicate a higher level of security for the upgraded approach. Xu et al. [16] built a third- order fractional chaotic system, which is emulated by a DSP circuit board, and then encrypted the image using compressed sensing and a block feedback diffusion framework to provide a larger key space and better flow conditions. Although the approach has a high mean structural similarity (MSSIM) index and speedy encryption speed, its anti-attack resistance is only moderate.

Two logistic maps are employed by Kamrani et al. [17] , which break a 128- bit key into two 64-bit keys, k1 and k2. A function with multiple multiplications and one division is used. The diffusion operation is carried out once after N iterations of the confusion operations. This N-round confusion process is repeated M times, then one diffusion operation is performed. The number of iterations can be regulated by setting M and N to 1 or any other value, which is what they leave open. It follows diffusion XOR, which is a random order. Gupta et al. [18] employed the NSGA-III algorithm to optimize a 4D map’s parameters, and they modified the parameters consists of the sum of the pixels in the preprocessed image. A chaotic system can operate with less efficiency. In the pre-processing stage, a vector I describing the input image is used to apply multiple XOR operations over the shift, and a vector V indicating the output picture is produced using a 32 x 32 Kronecker product. The product does not specify the technique used to obtain vector V, yet I XOR V results in a new image vector U. The variables of the 4D map are adjusted using the sum of all the pixels in U.

To improve the security of medical images, Akkasaligar et al. [19] employed chaos-based cryptography. The authors used chaotic sequences formed during the DNA decoding process to compress the input medical image, scramble [20] the pixels, and create a unique DNA image, which was then used to code the DNA rules and encrypt the sub images rule by rule. The cryptanalysis shows that the suggested cryptosystem is resistant to a variety of assaults. To test the similarity of the retained medical image, the compression ratio and pixel comparison are used.

Benssalah et al. [21] used chaos theory to digital imaging and commu- nications in medicine objects (DICOM), which contain highly private and associated patient-related data and are extensively employed in telemedical medical information systems (TMIS). The researchers use a logistic 2D coupled chaotic map, a linear congruential generator, and an XOR shift generator to construct the cryptosystem.

Using chaotic sequences generated by the logistic map that was optimised, Han et al. trained the hermit chaotic neural network. The method beat statistical analysis and enhanced the security of medical images with its high key sensitivity and vast key space. A novel 1D-cosine polynomial chaotic system with good chaotic dynamic performance was introduced by Talhaoui et al. [13] . The chaotic system is integrated with the conventional parallel shuffling and diffusion concept to encrypt an image.

Using chaotic sequences derived by the logistic map that was tuned, Han et al. [22] trained the hermit chaotic neural network. The method beat statistical analysis and enhanced the security of medical images with its high key sensitivity and vast key space. A novel 1D-dimensional cosine polynomial chaotic system with good chaotic dynamic performance was introduced by Talhaoui et al. [13] . The chaotic system is integrated with the standard parallel scrambling diffusion functionality to encrypt an image.

As a result of the continued use of a shifted scrambling diffusion structure in this technique, its security performance is subpar. A Butterworth High Pass Filter was utilized by Shalaby et al. [23] to enhance the security of DICOM images and prevent potential data loss during the encryption-decryption process (BHPF).

The strategy is based on the well-known Advanced Encryption Standard (AES) algorithm and Arnold’s cat map method. The CAT-AES technique can speed up the encryption-decryption process while lowering total computing expenses.

Most techniques in the literature are too sluggish and insecure to be used in crucial EHD privacy preservation. This study presents a 2D-LSCM [24] based encryption technique for EHD. The 2D-LSCM is made up of two maps: a sine map and a logistic map. The suggested technique is the first, loss less, and secure scheme for preserving the privacy of EHD conversations in real time. Due to their flaws, such as the fact that they only work with square images and have a large computational cost with relatively low security, the majority of encryption algorithms are unfit for medical image encryption. This paper put forth an encryption algorithm that works with any image size and format. The suggested method is small and efficient, making it suitable for real-time applications like the encryption of medical images.

The designed 2D sine-logistic coupled map (2D-LSCM), that is applied to generate PRNS, is shown in the subsequent sections, Section 2. The control scheme is explained in Section 3, and the security analysis of the findings is presented in Section 4. Section 5 presents the conclusion of the research article.

2.    Our Contribution

Three sections comprise up the operation described. The encrypted image CI is generated by (i) designing the new PRNG based on a new chaotic map called the Logistic-Sine chaotic map (2DLSCM), (ii) permuting the pixels in the plain image PI, and (iii) diffusing the pixels in the permuted image.

• •    Medical images are internally processed using machine level superfine granular arithmetic operations. Computer based high-level image processing operations cannot be applied on medical images. They do not produce the required functionality. Classical chaos-based image encryption algorithms (IEA) operate on analog and digital modalities, both of which are not suitable for the development of medical image encryption algorithm (MIEA).

• •    The Logistic and Sine maps serve as the basis for the LSCM’s design. Each of these two maps have a restricted key space and a chaotic region, in their original form. The novel 2DLSCM has larger key space and expanded chaotic region. In this paper, a Lyapunov exponent and a bifurcation diagram are utilized to quantify the 2DLSCM. The presented 2DLSCM is a double orbit chaotic map, unlike other 2DLSCM discussed in literatures.

• •    Two PRNS (R1 and R2) with dimensions equal to the number of rows and columns in the PI are generated in order to permute the pixels in the PI. The PI pixel at position (i, j) is switched with a pixel at position (R1(i), R2(j)).

• •    To diffuse the permuted pixels into 256-bit blocks, the hash value h produced by the SHA-256 method is XORed with the permuted pixels. For a minor variation in the input, SHA-256 generates a 256-bit hash code that is incredibly unpredictable. The row number of the permuted image is concatenated with a 256-bit nonce (number used just once) to make the hash generation secure. The secret key K contains the nonce. The key space for the system is theoretically unlimited. However, we have considered a very secure key space, which makes the scheme resistant to statistical and brute force attacks.

• •    The scheme was tested and evaluated with nine security measures, namely histogram analysis, correlation amongst the adjacent pixels in diagonal, vertical and horizontal directions, number of pixel change rate (NPCR), unified averaged changed intensity (UACI), peak signal-to-noise ratio (PSNR), mean squared error (MSE), entropy, deviations between the PI and the CI, and key-space analysis.

3.    Coupled 2D Logistic-Sine Map Development (2D-LSCM)

In the presented framework, we illustrate a 2D-LSCM created by utilising the logistic map and the sine map in 1D each. Eq. 1 e xplains the Sine [25] map. 1.

fu = ц sin (лК)                                             (1)

where initial condition x E [0,1], and control parameter 0 < u < 1. The Logistic map is defined by Eq. 2

hi + 1 = 0hi(1 - hi)                                        (2)

where initial condition h e [0, 1], and control parameter /? E [3.4,4]

However, two maps, the logistic and sine maps, have simple behavior and unstable chaotic intervals in high precision. As a result, we combine the two maps to obtain a new chaotic map with very complex chaotic characteristics, which we refer to as 2D-LSCM and which is given by Eq. 3

hi + 1 = sin(л(4шhi)') + (1 -                                (3)

bi + 1 = sin(л(4wbi)) + (1 - to)sun(лbi + 1)                          (4)

where the control parameter ω ϵ [0, 1]. As stated in its definition, the 2D- LSCM is generated by pairing the Logistic and Sine maps around each other, performing a sine transform on the coupling result, and then extending the dimension from 1D to 2D. The complexity of the Logistic and Sine maps can be appropriately blended in this method, resulting in complex non-linearities. The random residues (h, b) derived by the 2D-LSCM are shown in Fig. 1. It illustrates the chaotic and uniform behaviour of the LSCM in 2D.

4.    The Proposed Method

The encryption of electronically transmitted healthcare images is very challenging task. The transmission medium of medical images is completely different than the digital transmissions. Hence, existing chaos-based image encryption algorithms cannot be used in this concept. The proposed image encryption algorithm uses 2DLSCM to generate hybrid combination maps, one set for generating confusion keys and the second one for creating diffusion keys. The encryption algorithm is divided into two parts: (i) permutation of PI pixels, and (ii) diffusion of pixel values using XOR operations. The permutation-diffusion based encryption method uses both diffuse pixel values and pixel scrambling. The encryption process is described in Algorithm 1. The algorithm takes the PI as input and uses permutation and bitwise XOR to convert it to a CI. For permutation, PRNS R₁, R₂ are utilized, and for diffusion, PRNS R3. The 2D-SLCM map with three separate sub-keys k₁, k₂, k₃ is used to produce the pseudo random number sequences R₁, R₂, and R₃. The initial parameter (p0, q0) and the control parameter ω are combined to generate the key K as sub-key K_i = (p0, q0, ω). The overall process is demonstrated in Fig. 2. The image in figure 1, shows the pseudo random sequences hi and bi plotted from the 2D-LSCM.

0     0.1    0,2    0.3 0,4    0.5    0 6    0.7    0.3    0.9     1

Fig. 1. The h_t vs b , plot of 2D-LSCM map

5.    Experimental Results and Analysis

We do a security analysis of the proposed strategy in this section. As a result, five different EHSD images were chosen to evaluate the strength of the scheme, resilience, and scalability. Table 1 shows the varying sizes, types, and quality of those five photographs. Histogram analysis, correlation coefficients, PSNR, entropy, MSE, NPCR, and UACI, among other methods, are used to assess security. The scheme takes the same amount of time to encrypt and decrypt since both processes require the same number of computations. Table 1 also shows the required time in seconds for the various images.

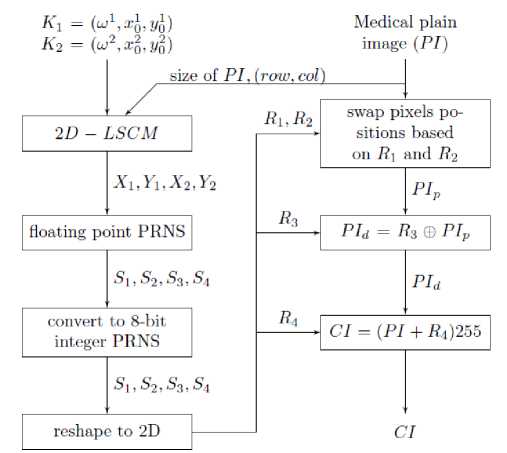
Fig. 2. The proposed method

Algorithm 1 Encryption Algorithm

• 1:    Dataln: PI, Key P₀, g₀, r₀, K

• 2:    DataOut: CI

• 3:    |A, B| = rows and columns in PI

• 4:    P,Q = 3Dlorenz(P0, g0, r0)

• 5:    kp= KSG(K)

• 6.    r=1,c=1

• 7:    for r=1 to A do

• 8:    PI(r) = Shiftcircular: PI(r) « P(r)

• 9:    end for

• 10:    for r = 1 to В do

• 11:    PI(c) = Shiftcircular: PI(c) « Q(c)

• 12:    end for

• 13:    for r = 1 to A do

• 14:    for c = 1 to В do

• 15:    CI(r,c) = PI(r,c) ф kp

• 16:    end for

• 17:    end for

• 18:    close

6.    Experimental Results and Analysis

• 6.1.    Histogram Analysis

• 6.2.    Correlation Coefficient (CC)

We do a security analysis of the proposed strategy in this section. As a result, five different EHSD images were chosen to evaluate the strength of the scheme, resilience, and scalability. Table 1 shows the varying sizes, types, and quality of those five photographs. Histogram analysis, correlation coefficients, PSNR, entropy, MSE, NPCR, and UACI, among other methods, are used to assess security. The scheme takes the same amount of time to encrypt and decrypt since both processes require the same number of computations. Table 1 also shows the required time in seconds for the various images.

Table 1. Size of test images and time consumed for encryption-decryption in seconds.

Image	No. of rows	No. of columns	Encryption or Decryption time (sec)
Test Image 1	223	226	0.010546
Test Image 2	243	207	0.010749
Test Image 3	225	225	0.015389
Test Image 4	244	206	0.0099339
Test Image 5	211	239	0.012312

Periodic representations of pixel values of an image compose histograms. An unauthorized individual can intercept the method using statistical assaults by determining the pattern of association between the intensity levels of the plain and CIs. As a result, the encryption technique must generate cipher image (CI) that are uniformly distributed. The histogram of pixel intensity levels of plainCIs of the five test images in illustration. 3 and illustration. 4. The histogram of the CIs is evenly distributed and flat, as can be seen. As a result, the attacker is left with no clues or high-risk data.

One of the most important instruments for statistical attacks is the correlation coefficient. Because of the considerable duplication in the PI, the CC is close to 1. In the CI, a valid encryption technique must lower the correlation coefficient to a null value. To measure the association of the pixels in the left, right, and diagonal directions, 12000 random pixel values are chosen from the image in each direction. In the illustration 5, the correlation coefficient between plain and CIs is displayed for Test Image 1 in all three directions.

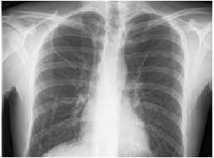
(a) Plain image (PI)

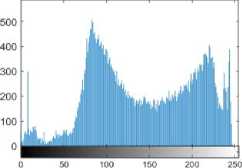
(b) histogram of PI

(c) cipher of PI (CI)

Fig. 3. Histogram comparison of the PI and CI using the Chest Front Lateral image.

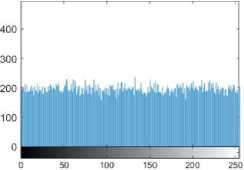
(d) histogram of PI

Image in figure 3(b) illustrates the histogram of Plain image (PI) 3(a) and Image in figure 3(d) illustrates the histogram of the encrypted image 3(c). The histogram of plain image has tonal distribution whereas the histogram of encrypted image is uniform.

Table 2. Comparison of correlation with ref. [7, 9, 14, 26] .

Image	Our Scheme	Ref. [7]	Ref. [9]	Ref. [26]	Ref. [14]
Chest Front Lateral	0.001278	0.003289	0.005473	0.002132	0.0042
Hand Xray	0.000382	0.000798	0.000567	0.000124	0.0223
Kidney Xray	0.004132	0.005437	0.004327	0.008765	0.0016
Normal Skull Xray Zephyr	0.002230	0.001423	0.005238	0.001411	0.0012
Skull	0.001663	0.001031	0.001679	0.001567	0.0091
Top Cortex of Skull	0.002476	0.000219	0.000224	0.000112	0.0055

Table 2 shows the estimated correlation coefficient values that are com- puted using the equation given below, which reveal that the CC of the CIs is extremely high and comparison with ref. [7, 9, 14, 26] .

СС _ ЕУ(Х₁-цХ₁)(Х₂-цХ₂)] аХ_г 0X2

where X 1 and X 2 are the corresponding standard deviations and σ X and σ X are a subset of chosen nearby pixels.

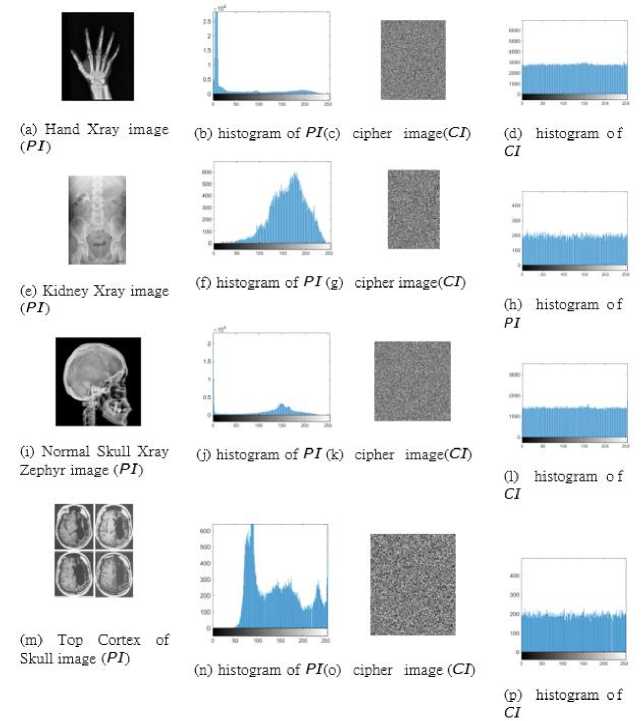
Fig. 4. Histogram comparison of the PI and CI using the 4 different test images. The image in figure 4(b) is the histogram of hand x-ray (PI) and image 4(d) is the histogram of the encrypted hand x-ray (CI). The image in figure 4(f) is the histogram of kidney-xray (PI) and image 4(h) is the histogram of the encrypted kidney x-ray (CI). The image in figure 4(j) is the histogram of Skull x-ray zephyr (PI) and image 4(l). is the histogram of its encrypted (CI). The image in figure 4(n) is the histogram of Skull top Cortex (PI) and image 4(p). is the histogram of its encrypted (CI). The histogram of encrypted image has tonal distribution whereas histogram of its encrypted image is uniform.

• 6.3.    Entropy

Entropy is used to measure the randomness of data distribution. In terms of bits, the information entropy measures the amount of unpredictability in a data source. If we take a gray level image to be information postulates, the magnitude’s randomness is 8-bit. The entropy is given by Eq. 6 to achieve extreme randomness in the cipher, the variations in entropy in CIs should be high. The entropy value of 8 is considered as the best value. An IEA obeys strong randomization principle if its entropy of PI and CI both is 8.

^E = - XL 0 P i log(P i )

The equation 6 above is a measure of Shannon’s entropy. In IEA, the Shannon’s entropy is used to detect the probability of occurrence of each possible state in chaotic trajectory to count the randomness and complexity of chaotic regime in 2DLSCM for IEA. The table 3, below shows the comparison entropy improved in our proposed scheme compared to existing in literatures.

Horizontal

О 50     100     150     200     250

(a) correlation of PI in HD

(b) correlation of CI in HD

(c) correlation of PI in VD

О 50    100   150   200   250   300

(d) correlation of CI in VD

(e) correlation of PI in DD

(f) correlation of CI in DD

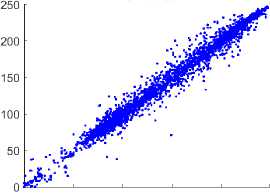
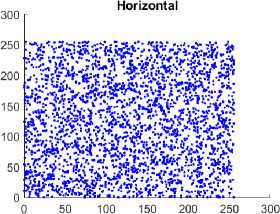
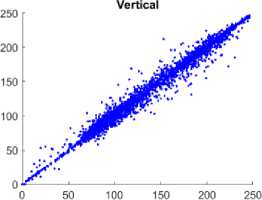
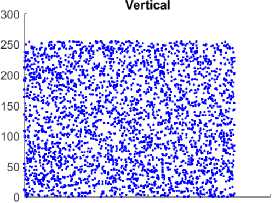
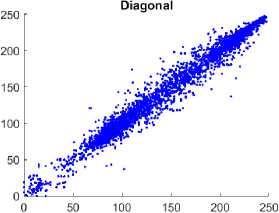
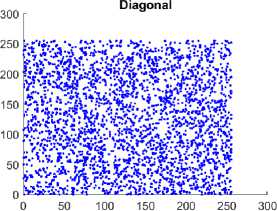
Fig. 5. Comparison of Correlation among the adjacent pixels in horizontal, vertical, and diagonal direction among the plain and CI using the Chest Front Lateral image. Figure 5(a), 5(c), 5(e) illustrates the distribution of pixels of the plain image which is linear, and the pixels lie on the main diagonal. Figure 5(b), 5(d), 5(f) illustrates the distribution of the pixels of the encrypted image is more scattered indicates absence of correlation between the neighborhood pixels.

Table 3. Comparison of entropy with ref. [7, 9, 14, 26]
Image	Our Scheme	Ref. [7]	Ref. [9]	Ref. [26]	Ref. [14]
Chest Front Lateral	7.9967	7.9791	7.5112	7.1267	7.1267
Hand Xray	7.9994	7.6512	7.2777	7.5643	7.9361
Kidney Xray	7.9963	7.9213	7.3341	7.9563	7.1876
Normal Skull Xray Zephyr	7.9992	7.6679	7.2579	7.9361	7.9642
Skull	7.9962	7.5568	7.2358	7.9112	7.9112
Top Cortex of Skull	7.9973	7.9236	7.7824	7.2364	7.2364

• 6.4.    Perceptual Security and PSNR

• 6.5.    Mean Square Error (MSE)

Peak signal to noise ratio is a factor to determine the excellence of two images (PSNR). The peak error is indicated by the PSNR. The upper limit of contam- inating noise that can impair the accuracy of its representation is determined by the peak signal to noise ratio. Without the secret key, recovering PI from a CI becomes difficult if the PSNR value is the lowest.

Table 4. Comparison of PSNR with ref. [7, 9, 14, 26]

Image	Our Scheme	Ref. [7]	Ref. [9]	Ref. [26]	Ref. [14]
Chest Front Lateral	39.775	39.198	39.457	39.543	29.156
Hand Xray	51.978	38.245	38.347	38.634	29.456
Kidney Xray	36.145	39.654	39.774	39.774	28.213
Normal Skull Xray Zephyr	48.769	38.627	37.324	38.875	28.912
Skull	39.324	46.298	46.554	47.179	27.798
Top Cortex of Skull	37.707	39.432	39.241	39.372	26.765

An encrypted image’s sensitivity to small changes in the PI, which implies that even a single pixel modification might have significant adverse effects, is often regarded to be one of its most desired qualities. The peak signal-to- noise ratio is used to evaluate the effectiveness of image compression. Table illustrates the measured PSNR values as shown in table 4 and comparison of with ref. [7, 9, 14, 26].

The PSNR assesses the cumulative squared error, whereas the MSE analyzes the peak error between the original and compressed images. Mean square error is one of the most often used indicators for quality degradation. According to Eq. 7, the metrics used to gauge encryption and decryption efficiency are MSE and PSNR. The table below displays the MSE values that were determined. Table 5 shows the MSE values that were calculated and comparison with ref. [7, 9, 14, 26] .

MSE=—^^(мЭ-ШУ)]2                 (7)

^{p x} Q (t,n

Table 5. Comparison of MSE with ref. [7, 9, 14, 26]
Image	Our Scheme	Ref. [7]	Ref. [9]	Ref. [26]	Ref. [14]
Chest Front Lateral	94.957	96.865	82.756	82.587	107.567
Hand Xray	175.23	98.664	89.458	89.776	107.689
Kidney Xray	81.432	97.156	95.426	95.749	106.453
Normal Skull Xray Zephyr	139.44	91.445	84.776	79.459	108.765
Skull	106.95	112.237	123.625	112.364	124.758
Top Cortex of Skull	90.204	95.674	92.654	91.957	105.876
6.6. NPCR and UACI

NPCR and UACI are widely used to determine key sensitivity. A strong encryption method should, according to Kerchoff’s model, be extremely sen- sitive to any mismatch in the secret key, which means that even a small modification in the secret key will produce a significant change in the CI. The avalanche effect demonstrates how a small modification in the plaintext can result in a huge modification in the key and plaintext.

n = t0, If РКм^РГа,!)

Р(1,п  \fif Р1(1,П*РГ(1,В                             (8)

where O (i, j) is a vector with components 0 and 1 if pixel value O (i, j) = O ′ (i, j) and O (i, j) ̸=′ O (i, j) respectively. The NPCR is given by Eq.9.

NPCR = ^ ^p(,^l,j) x 100%                               (9)

When contrasted to other schemes that are provided in, the econometric findings of NPCR are more beneficial and trustworthy and are illustrated in Table 6 and also compared with ref. [7, 9, 14, 26] . UACI is a measure which detects the average differences in the intensity of plain images and ciphered image. A specific value of around 33 is considered as good quality of an encryption.

Table 6. Comparison of NPCR with ref. [7, 9, 14, 26]

Image	Our Scheme	Ref. [7]	Ref. [9]	Ref. [26]	Ref. [14]
Chest Front Lateral	99.699	99.651	99.212	99.141	99.623
Hand Xray	99.787	99.634	99.516	99.412	99.595
Kidney Xray	99.635	99.332	99.288	99.191	99.570
Normal Skull Xray Zephyr	99.794	98.231	99.327	99.235	99.610
Skull	99.637	98.378	99.617	99.214	99.134
Top Cortex of Skull	99.646	99.678	99.129	99.282	99.543

The UACI is given by Eq. 10.

UACr = ^p(l,j) p,(l,j) x 100%

F/T

The values of UACI are computed by modifying five-pixel values in each of the PIs to yield the CI values. In Table 7 the calculated UACI results are presented and also comparison with ref. [7, 9, 14, 26] .

Table 7. Comparison of UACI with ref. [7, 9, 14, 26]

Image	Our Scheme	Ref. [7]	Ref. [9]	Ref. [26]	Ref. [14]
Chest Front Lateral	31.309	31.27	29.28	29.129	33.4588
Hand Xray	43.67	29.129	28.312	28.214	33.5075
Kidney Xray	29.286	28.819	31.27	31.258	33.4277
Normal Skull Xray Zephyr	38.191	31.258	31.27	29.28	33.4121
Skull	33.164	28.214	28.819	31.27	33.1633
Top Cortex of Skull	30.596	29.28	28.214	30.148	32.3801

7.    Conclusion

The proposed method is implemented to secure medical images in different modalities. The results of experiments conducted on the prototype images show that the proposed algorithm is comparatively fast and robust in terms of computation and security aspects. The level of security is assessed using NPCR and UACI which show empirical values on the prototype images taken for testing. The correlation coefficient and the histogram analysis prove the accuracy of the presented encryption technique for DICOM objects and medical images. The results of analysis show theoretically best values when evaluated on different test images. The strength of the proposed scheme is the high degree randomization of pixels in confusion-diffusion using 2DLSCM.

This paper presents a 2D-SLCM based image encryption for DICOM objects. A 2D-SLCM-based encryption technique for EHSD is provided. The pixel values in the scrambled image were first scrambled and then diffused by the PI. The results of the tests and analysis reveal the security aspects of theorized EHSD. The use of control variables p0(16bits), q0(16bits), ω(16bits) each of 216+16+16 gives 248+48+48 that is 2144 bits as input for each subkey in k1, k2, k3. Thus, the space achieved is 3*48 + 2*64 = 272 bits is the initial seed value for iv1 and iv2 given to produce K1 an K2. Therefore, the total keyspace achieved is 2272+272 is 2544 bits (2^544bits). The acquired keyspace is substantial to produce unique key for each block in transmission. The operations performed to generate the proposed algorithm are mathematical operations which do not involve any image processing operation. Thus, the method is uniquely designed to encrypt medical images. None, of the methods in the existing literatures using similar concept of 2DLSCM is developed through mathematical modelling, specific for e-healthcare transmission.

Encryption method is safe, effective, robust, and scalable, and that it can with- stand a variety of vulnerabilities. The most significant benefit of the scheme is that it has extremely fast encryption and decryption times, which is a peculiar characteristic.

Conflict of interest and Data Availability

The authors hereby declare that there was no full or partial financial support from any organization. The authors do not have any conflicts of interest to disclosures. The data used in the research is available freely. The code is written and available with the authors.