Fast Time-varying modal parameter identification algorithm based on two-layer linear neural network learning for subspace tracking

Published Online February 2011 in MECS

The key of algorithms based on subspace tracking is to find an efficient and fast algorithm for subspace tracking. The signal subspace obtained by PAST converges asymptotically to the orthogonal subspace, by introducing orthogonal method W = W (WTW)-1/2 OPAST[18] is obtained. Otherwise by deflation technique of PCA(Principal Component Analysis), PASTd[17,19] is derived. Similarly, signal subspace obtained by PASTd has a strong lose of orthogonality, by introducing orthogonal method Gram-Schmit for incorporating characteristic of PASTd, a modified PASTd[20] is obtained. PAST can be viewed as a classical power iteration method. Comparing with PAST, NPI[21,22](Natural Power Iteration) has a faster convergence speed and ensures orthogonality of subspace vectors without compute load increasing. In both PAST and NPI, Wp+1 ® Wp is used in the process of algorithm derivation, so they are only suitable for tracking slow subspace. Different from PAST and NPI, API[23](Approximated Power Iteration) can track rapid subspace and apply updating data in both infinite exponential window and finite moving exponential window. Different from PAST in cost function, NIC[24,25](Novel Information Criterion) is proposed, adopting in two-layer linear neural network learning for subspace tracking. By introducing orthogonal method, a modified version is obtained named FONIC[26].

This paper presents a modified version of NIC adopting in two-layer linear neural network learning for subspace tracking. Comparing with the original algorithm, there is no need to set an important parameter in advance. Simulation experiments show that it has a faster convergence in the initial period.

• 2.    Modal parameter identification algorithm based on ED/SVD

The state-space model of linear time-invariable system of n /2 order is denoted as follows:

x ( k + 1) = Ax ( x ) + Bu ( k ), y ( k ) = Cx ( k ) + Du ( k )

Where x ( k ) e R" ^{x 1} is the state vector at the k ^th sampling instant, A e R " ^x " is the system state matrix, B e r " ^x m is the input matrix, u ( k ) e R m ^{x 1} is the corresponding input vector at the k ^th sampling instant, C e R^{r x} " is the input matrix , D e R ^{r x} m , y ( k ) the output vector.

Constructing Hankel matrix by input/output vectors respectively, we have:

U P =		■ u (1) u (2) M	u (2)     - u (3)     -	u ( P ) u ( p + 1) M		(2)
Y p =	[	_ u ( M ) y (1) y (2)	u ( M + 1) - y (2) - y (3) -	u ( p + M — 1 y ( P ) y ( P + 1) M	) _	(3)
Furth YU - pp Wher	_ y ( M ) y ( M + 1) — y ( P + M — 1) _ er we get = Y p — Y p U P ( U p U P ) - 1 U p = Г XU - = u-=I-UT(U UT —AU , Ppppp ,				I	(4) is an
identity matrix, Г			= [ C CA	— CAM —1"	T	is the
generalized			observability			matrix,

X = [ x (1) x (2) ”• x (p )] is a matrix constituted by state vector, superscript (D) T denotes matrix transpose.

Do singular value decomposition(SVD) on Y_pU - , we have:

YU ^±=[P Pl pp s n

2 ,   0

. 0 2 "

V s^T

V n^T

Where    P s   is estimate of Г . For

Y P U P ^{- (Y} p ^U p ) T = YPU P Y" , ^eig^en-decomp^osition(ED) on Y_pU - Y p can be used to extract left-singular matrix block P s of Y_pU ^- . By (4), we have:

A = Г+Г2

A = ФЛФT (7)

Where Л = diag ( X X 2 -■ X 2" ) and X i = X * ₊ " , superscript * denotes conjugate. By modal analysis theory, we get:

и = 7(XR )2+ (X' )2, X = —XR / и, (8)

Where to i and C i are the natural frequency and damping ratio respectively of the i t order, Xp and X , are the real and imaginary parts respectively of eigenvalue X . In general, natural frequency and damping ratio are included in modal parameters. Here in this paper we focus on time-varying frequency identification.

• 3.    Pre-treatment on the updating input/output data

From the second part, evidently each step eigen-decomposition on Y_pU _p Y P costs a large memory space and computation load. Otherwise there is no need to evaluate Y_pU - Y p and do eigen-decomposition on Y_pU_p Y p for extracting its eigen-matrix in the timevarying modal parameter identification algorithm based on subspace tracking. By adopting recursive form of updating input/output data, principle subspace tracking algorithm can be applied and then fast identification of time-varying modal parameter is achieved. Updating the input and output Hankel matrix, we have:

Y p + i = [ Y p У_Р + 1 ], U p + i = [ U p U p + 1 ]    (9)

Where yp+1 =[yp+1) yp+2) L yp +M], up+1 = [u (p+1) u (p + 2) ^ u (p+M) ]T.

By lemma of matrix inverse

( A + xx^T ) ^{- 1} = A ^{- 1} - A ^{- 1} xx^T A ^{- 1} / (1 + x^T A ^{- 1} x ) (1°) We have:

Y p UY = Y p UY + Z p + 1 ^x  (11)

Where Z p1 A YU(U p U T )X - L -L^, ti p +1 = u T + 1 (U p Up ) ^{- 1} u p +1 . Equation ⁽¹¹⁾ is called rank-one updating. If there is no persistent excitation, namely exciting by initial displacement or velocity conditions, then we have z_{p +1} = y _{p +1} , U p E C^{p x p} identity matrix. Such condition is common in the engineering field. Both are referred in this paper.

• 4.    Time-varying modal parameter identification algorithm based on neural network learning

After getting the recursive form of updating input/output data, the key of fast identification of timevarying modal parameters is efficient and fast algorithm for subspace tracking. The following is to state the algorithm based on linear two-layer neural network for subspace tracking.

The cost function[23,24] is chosen as:

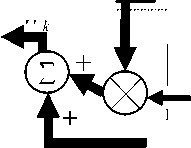
J nic (W k ) = jw^ W T R ( kW k )] - Г WX )} (12) Where W_k is the signal subspace at k ^th instant.

R_zz ( k ) = L в - iz^T , ° <  в <  1 is the forgetting factor, i = 1

tr ( D ) denotes matrix trace.

By partial differential of matrix trace, we have:

J ( W k ) = R zz ( kXWR ( k ) W ) ^{- 1} - W (13) Further we have:

W = W k - 1 + n V J„ C (W k )    (14)

W = (1 -n k ) W - 1 +n R ( kW ( WR ( kW ) ⁴,15) Let y k = W k - 1 z k , we get,

W k = (1 -n k )W - 1 +n R y ( k ) R 1 ( k ) (16)

kk

Where R, ( k ) = £ в Ay T , R , ( k ) = Z в - i yy T - = 1                                       i = 1

By lemma of matrix inverse,

( A + zz^T ) ^{- 1} = A ^{- 1} - A ^{- 1} zz^T A ^{- 1} /(1 + z^T A ^{- 1} z ) , We get

W k = (1 - n k ) W k - 1 + n_kW_k     (17)

и; = W ,-1 + ( z k - W k - 1 y k ) У Г Д-, /( в + y k P k -, y k ) . W k -1 = R z, ( k - 1) P k -,,

P k = (Ilin' ) " ‘ = ( PR„ ( k - 1) + iX ) ^{- 1}

= 1

.

_n ⁽ Pk -1    _n t ух )

Different from the original method, n _k is not set in advance. Applying Differential segment,

6nk dJNIC (Wk )

Let dHk

a W k    6n k

= ° , we have:

(zt -W-y„))TP.ч/(в+yTP.-кУк)

k r ’kA

Where ||D| denotes Frobenius norm of matrix.

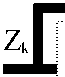
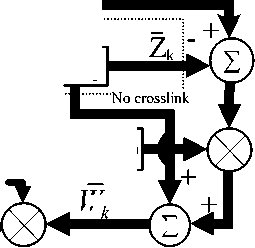
Linear two-layer NN

T

W k - 1

W

У

y T P k - 1 /( P + y ' P k - y )

,   n k

1 - n k

W

I

Fig. 1 Algorithm block based on linear two-layer neural network learning for subspace tracking

According to the modified version mentioned above, we get the algorithm block based on two-layer linear neural network learning for subspace tracking showed in Fig.1. Further we get the fast identification algorithm of time-varying modal parameters.

Further construct the system matrix A ( k ) by W_k ,

Ук„ r^-—► wk.,

repeating (6), (7) and (8) for extracting time-varying modal parameters. The whole procedure of the timevarying modal parameter identification algorithm based on two-layer linear neural network learning for subspace tracking is showed as follows:

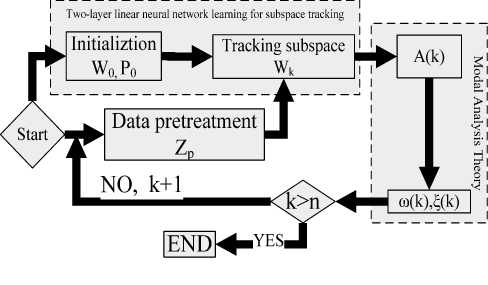
Fig.2 Flowchart of identification algorithm for time-varying modal parameters

• 5.    Simulation and Analysis

Moving mass-beam structure is widely used in modelling bridge with moving vehicles, truss with moving crane and so on, which is a typical time-varying structure. Supposing that moving mass keeps contact with beam all the time, neglecting torsion deformation of beam, applying Euler-Bernoulli beam theory, we get the model as follows:

_EI ∂ ⁴ y ( x , t ) _{+ m} ∂ ² y ( x , t ) _{= F ( x , t )       (20)}

∂ x ⁴            ∂ t ²

Where E is Young’s modulus, I is the second moment of beam cross-section, m is the mass per unit length of beam, y ( x , t ) denotes the transverse deflection of beam, F ( x , t ) is time-varying driving force. Taking the inertia load of moving mass into account^[27], we have:

• 1             ∂2y(x,t)

F ( x , t ) = [ - m ₀ g - m ₀       ][ H ( x - ξ + ) -

ε             ∂t2

H(x-ξ-ε2)]-f(t)δ(x-l)(21)

Where m ₀ is the moving mass, g is the gravitational acceleration, H ( □ ) is Heaviside unit function, f ( t ) is external excitation force, ^ ( D ) is Dirac-Delta function, ξ = Vt , V = const the moving speed of moving mass. And the other parameters are showed in Fig. 2.

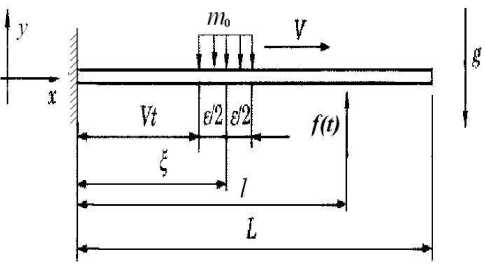
Fig. 3 Moving distributed mass-Cantilever structure

∞

Let y(x,t) = ∑φi(t)Xi(x), with φi(t) is i =1

unknown functions of time and Xi (x) is the shape th functions for the i mode of the vibration beam, which are chosen to be known. Substituting them into (20) and (21) , we have:

M ( t ) Φ ^''( t ) +Ω ² Φ ( t ) = F ( t )

M ( t ) = ^e I ^re n ^: + diag ( m i ) m 0 [ X ( ξ ) X^T ( ξ )

+ ^ε ₂₄ ( X ( ξ ) X^T ( ξ ) Λ ²

+ 2 Λ X ( ξ ) X^T ( ξ ) Λ+Λ ² X ( ξ ) X^T ( ξ )]

Λ = diag ( β _i )

X ( x ) = [ X 1 ( x ) L X,( x ) l X n ( x ) f

Ф ( t ) = [ ф ( t ) ..ф( t ) ™ ф _п ( t ) f , I_n E C n ^X n

,

, identity

matrix, Q = diag( to i ) , diag ( □ ) denotes diagonal matrix, ω _i ² = β _i ⁴ EI / m , X_i ( x ) should be chosen to meet                                             that

X ( x ) - β ⁴ X ⁽⁴⁾( x ) = 0 , m = m^LX ²( x ) dx ,

F ( t ) =- diag ( m i ) m 0 g ( I n + ^ε ₂₄ Λ ²) X ( ξ ) + f ( t ) X ( l )

The dimension of beam is 1.2 × 0.05 × 0.008 m,

V = 0.2 m/s, EI = 418.13       N.m²,

ξ = 0.07 m, l = 1.0 m,

X_i ( x ) = cosh( β _i x ) - cos( β _i x ) -

cosh( β _i ) + cos( β _i ) sinh( β _i ) + sin( β _i )

(sinh( β _i x ) - sin( β _i x )) , β _i  is determined by

• 1    + cos( e L)cosh( e L ) = 0 , i = 1 l n , n takes a limited value as n = 4 .

The identification results of time-varying modal parameter identification algorithms based on different subspace tracking methods, such as the original NIC, the modified NIC presented in this paper and FONIC, are showed in Fig. 4 and 5. The output data incorporates stochastic white noise of signal-noise ratio SNR=43db.

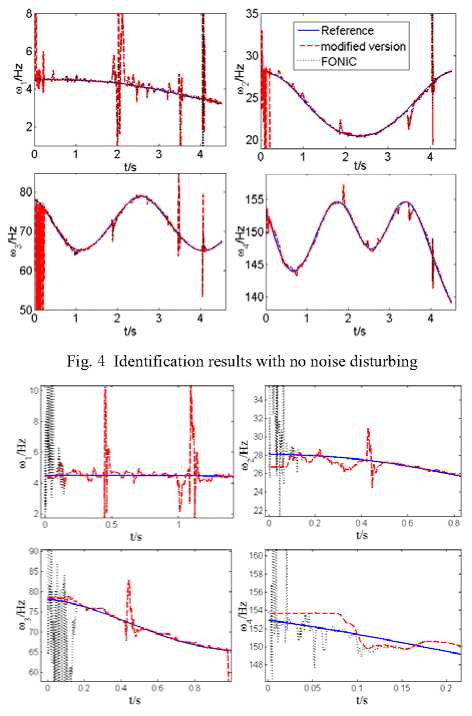
Fig. 5 Identification results with noise disturbing

By Fig.3 and Equation (22), its natural frequencies of the moving distributed mass-cantilever structure change along with time. In Fig.4, the real blue curve denotes theoretic results for reference, with the red dash curve denoting identification results obtained by applying time-varying modal parameter identification algorithm based on modified NIC,which is adopted in two-layer linear neural network learning for subspace tracking and the black dot curve denoting identification results obtained by using time-varying modal identification algorithm based on FONIC. As is shown in Fig. 4 , timevarying modal identification algorithm based on modified NIC has an equivalent performance with that based on FONIC. Otherwise due to adopting orthogonal method in FONIC for subspace tracking, its computation load is greater than that of modified NIC. As is showed in Fig.5, all of the three time-varying modal parameter identification algorithms based on different subspace tracking method have a good tolerance of noise. Showed In Fig.5, evidently the time-varying modal parameter algorithm based on modified NIC, which is adopted in two-layer linear neural network learning for subspace tracking, has a faster convergence speed in the initial period.

To test its performance of the time-varying modal parameter identification algorithm based on two-layer linear neural network learning for subspace tracking, a experiment of cantilever beam with removable mass is designed. Such an experiment is divided into three parts. First test its natural frequencies of cantilever beam with removable mass on it by applying conventional modal analysis method, such as Power Spectrum Density Analysis. Second repeat the first part on cantilever beam without removable mass on it. Third sample its vibration response data in the form of acceleration excited by shock and remove abruptly the moveable mass in the data sampling procedure. Do data processing by using the time-varying modal parameter identification algorithm based on two-layer linear neural network learning for subspace tracking presented in this paper. The experiment equipment is showed in Fig.6. There are two piezoelectric accelerometers, a cantilever beam, a removable mass, a hammer used as plus excitation, a set of data collecting system named DASP V10 showed in Fig.6 and data processing system ,mainly a set of modal analysis software and corresponding hardware, doesn’t be showed in Fig.6.

Fig.6 the experiment equipment out of work

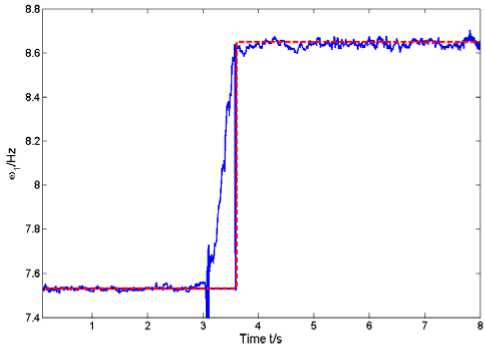
Fig.7 the first-order abrupt natural frequency

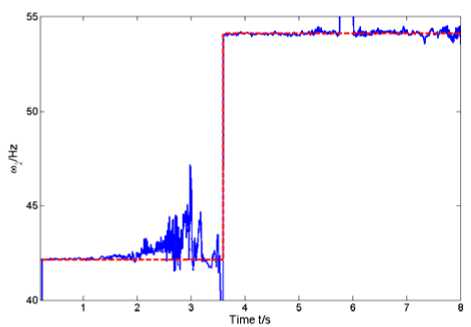
Fig.8 the second-order abrupt natural frequency

In Fig.7 and 8, the blue real curve denotes the identification results with the red dash curve denoting the testing value for reference. In Fig.7 the first-order natural frequency changes from 7.53Hz to 8.65Hz and in Fig.8 the second-order natural frequency changes from 42.1Hz to 54.1Hz. Evidently we can foresee change of natural frequencies in the third part of the designed experiment. And identification results showed in Fig. 7 and 8 just coincide with what we test, which confirms its performance of the time-varying modal parameter identification algorithm based on two-layer linear neural network learning for subspace tracking presented in this paper.

• 6.    Conclusion

The key of fast identification algorithm of timevarying modal parameters is to find efficient and fast signal subspace tracking algorithms. This paper applies the modified NIC adopted in two-layer linear neural network learning for subspace tracking to achieve fast identification algorithm of time-varying modal parameters. For the modified version of NIC, using in two-layer linear neural network learning for subspace tracking, there is no need to set an important factor in advance and has a faster convergence speed in the initial period demonstrated by simulation experiment results. And real experiment under laboratory conditions confirms its validity of the time-varying modal parameter identification algorithm presented in this paper in extracting time-varying modal parameters.