Фазовая диаграмма системы BaO-PbO-Fe2O3

Исследование физико-химических параметров, обеспечивающих стабильное образование кристаллов гексаферрита бария BaFe 12 O 19 и твердых растворов на его основе из оксидных систем [1], требует детальной информации о фазовых равновесиях, реализующихся в многокомпонентных системах. Одним из наиболее распространенных оксидов-растворителей, используемых для получения кристаллов гексаферрита из оксидного расплава (флюса), является оксид свинца. В рамках настоящей работы была поставлена задача проведения термодинамического анализа системы BaO–PbO–Fe 2 O 3 , моделирования фазовых равновесий, реализующихся в этой системе, что является чрезвычайно важным, поскольку позволит определить концентрационные и температурные интервалы, обеспечивающие кристаллизацию гексагонального феррита из оксидного расплава.

Термодинамическое описание тройной системы требует предварительного описания двойных систем BaO–Fe 2 O 3 , PbO–Fe 2 O 3 , BaO–PbO.

В настоящее время некоторые сомнения остаются даже о виде диаграммы состояния бинарной системы BaO–Fe₂O₃, которая является основой этого класса систем [2–8]. При описании этой системы мы использовали самые надёжные литературные данные, а также собственные данные о температурах плавления ферритов бария. Обзор данных о системе PbO–Fe 2 O 3 , вместе с результатами нашего моделирования этой системы, представлен в работе [9]. Для описания фазовых равновесий в системе BaO–PbO использованы результаты собственного экспериментального исследования. Изучалась область низкотемпературных расплавов системы BaO–PbO с преобладанием оксида свинца. Для этого использованы два подхода. Во-первых, с помощью печи сопротивления исследовались температуры плавления и гомогенизации предварительно подготовленных смесей оксида свинца и карбоната бария заданного состава. После охлаждения образцы подвергались рентгеноспектральному исследованию с целью определения полноты разложения карбоната бария. Показано, что во всех образцах в условиях эксперимента произошло полное разложение карбоната, в пользу чего свидетельствует факт отсутствия в них углерода. Также для определения температуры точки эвтектики было проведено исследование одного образца методом ДТА. Результаты моделирования вместе с результатами проведённых экспериментов представлены на рис. 1.

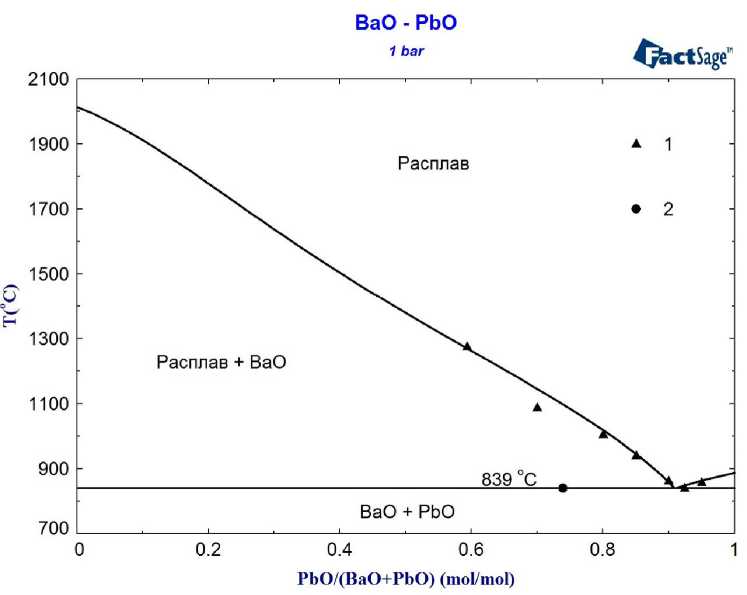
Рис. 1. Фазовая диаграмма системы BaO–PbO. Экспериментальные данные настоящей работы: 1 – температура гомогенизации расплава; 2 – ДТА

Используемые методы

В процессе исследования для подбора термодинамических характеристик, оптимизации модельных параметров и расчёта фазовых диаграмм использовался программный комплекс FactSage (версия 7.0) [10, 11], произведённый Thermfact (Canada) and GTT Technologies (Germany), и созданные в процессе исследования базы термодинамических данных, ключевые данные о содержании которых представлены в табл. 1–3. Значения термодинамических функций отчасти заимствованы из литературных источников, а отчасти стали результатом оптимизации параметров с целью получения согласующейся с экспериментальными данными картины фазовых равновесий в моделируемой системе. Данные для описания PbO и Fe₂O₃ заимствованы из базы SGPS (SGTE pure substances database, v13.1, 2013), данные для газообразного BaO, а также ΔH 298 , S 298 , T пл и ΔH пл для оксида бария заимствованы из базы FactPS (FACT pure substances database, 2015).

Таблица 1

Термодинамические характеристики оксида бария

BaO (твёрдый) 298.150–799.109 K 799.109–2286.000 K	ΔH 298 = –548104 Дж/моль            S 298 = 72.069 Дж/(моль ⋅ K) C p = 48.8610816 + 0.0088948188 ⋅ T – 379724.7031/T2 * C p = 50.610128561 + 0.006918282002 ⋅ T – 494977.8498/T2 *
BaO (жидкий) 298.150–643.773 K 643.773–1600.010 K 1600.010–5000.000 K	T пл = 2286 K                 ΔH пл = 59000 Дж/моль C p = 47.972692738 + 0.010207731 ⋅ T – 333748.541/T2 * C p = 51.320488471 + 0.006589285554 ⋅ T – 755792.448/T2 * C p = 66.944 *

* – результат аппроксимации данных, представленных в справочнике [12].

Таблица 2

BaFe 2 O 4 (твёрдый) 298.150–2500.000 K	AH 298 = -1518000 Дж/моль *          S298= 123,2 Дж/(моль - К) * C p = 138.6 + 0.08742 - T - 929857.89/T2 [13]
BaFe12O19 (твёрдый) 298.150–725.000 K 725.000–2000.000 K	AH 298 = -5698000 Дж/моль *          S298= 52 8,6 Дж/(моль - К) *
	C p = 348.6 + 1.16882 - T [14] C p = 695.79 + 0.1546 - T [14]
Ba2Fe2O5 (твёрдый) 298.150–2500.000 K	AH2 98 = -2109000 Дж/моль *          S298= 189,2 Дж/(моль - К) * C p = 187.1 + 0.09592 - T - 1278526.46/T2 [13]
Ba 2 Fe 6 O 11 (твёрдый) 298.150–2500.000 K	AH 298 = -3 8 9 1 800 Дж/моль *           S2 98 = 3 65,7 Дж/(моль - К) * C p = 398.94 + 0.1195 - T - 5991000/T2 [14]
Ba 3 Fe 2 O 6 (твёрдый) 298.150–2500.000 K	AH 298 = -2660300 Дж/моль *          S298= 262,8 Дж/(моль - К) * C p = 235.6 + 0.10443 - T - 1627195.02/T2 [13]
PbFe4O7 (твёрдый) 970.000–1050.000 K 1050.000–1160.000 K	AH 298 = -18 3 7 3 95 Дж/моль *          S2 98 = 275,85 Дж/(моль - К) * C p = -68799.35733 + 87.02944168 - T + 12912092477.8/T 2 -- 0.030796877225256 - T 2 ** Cp = 205.71869 + 0.12491108 - T + 33091497.8/T2 - 2.4726305256E-5 - T 2 **
PbFe 12 O 19 (твёрдый) 298.150–700.000 K 700.000–955.000 K 955.000–970.000 K 970.000–1050.000 K 1050.000–1160.000 K 1160.000–1812.000 K	AH 298 = -5118 5 00 Дж/моль *          S298= 643,74 Дж/(моль - К) * Cp = 907.27067 - 0.20773212 - T - 19161642.2/T2 + 0.000433515974744 - T2  ** C p = 3873.31667 - 5.77101972 - T - 268774962.2/T 2 + + 0.003367378574744 - T2  ** C p = -30250095.03733 + 41449.15926168 - T + 4774754120477.8/T2 - - 15.9732899972253 - T 2   ** C p = -206487.99733 + 261.06180168 - T + 38736836477.8/T2 -- 0.092390637225256 - T 2   ** C p = 527.23073 + 0.34820988 - T + 99833537.8/T2 - 7.4184465256E-5 - T2  ** Cp = 542.410281966394 + 0.3349482 - T + 100113060/T2 - 7.418724E-5 - T2 **
Pb 2 Fe 2 O 5 (твёрдый) 700.000–955.000 K 955.000–970.000 K 970.000–1050.000 K 1050.000–1160.000 K	AH 298 = -12 1 6 8 80 Дж/моль *          S298= 272,8 Дж/(моль - К) * C p = 727.98434 - 0.93752354 - T - 45308284.4/T2 + 0.000561234849488 - T2  ** C p = -5041600.07466 + 6908.21752336 - T + 795791840955.6/T2 - - 2.66221499445051 - T 2   ** C p = -34332.23466 + 43.53461336 - T + 6455626955.6/T2 -- 0.015398434450512 - T2  ** C p = 170.30335 + 0.08234806 - T + 16126465.6/T2 - 1.2358990512E-5 - T2  **

Термодинамические характеристики двойных оксидов

* – результат оптимизации.

** – рассчитано по правилу Неймана – Коппа, опираясь на данные для PbO и Fe 2 O 3 .

Таблица 3

Параметры модели, определённые в работе и использованные для описания оксидного расплава

Система	Значения параметров, Дж/моль
BaO–Fe 2 O 3	LBa 2 + F 3 + O - =" 250000
	LBa 2 +        = 20000
	LBa 2 + ,Fe 3+ю2 - = 50000
BaO–PbO	LBa 2 + ,Pb 2+»2 - = 66000 - 69T
	LB a 2 + ,Pb 2+»2 - = 4 30 00 - 29T
Fe 2 O 3 –PbO	L 0 Fe 3 + P :0 2 - = -31026 +5,054T
	L 1Fe3 + ,Pb 2 + : 0 2 - = -10315 +12,793 T

Окончание табл. 3

Система	Значения параметров, Дж/моль
	Ba2+T                  -0 L Ba2 + ,Fe3 + , Pb2 + : O2 = 0
BaO–Fe 2 O 3 –PbO	Fe3 ' L B.-JC 3 + , - 2 - 0 2 - = — 300000 Pb2 + L Ba 2 + ,Fe 3 + , Pb 2 + : o 2 - = —500000

Для описания энергии Гиббса оксидного расплава для всех исследуемых систем использована двухподрешёточная модель ионной жидкости [15, 16]. Компонентами катионной подрешётки считаются положительные ионы (Ba2+, Fe3+, Pb2+). Анионная подрешётка состоит из ионов O2–. Для описания отклонения раствора компонентов подрешёток от идеальности использовались полиномы Редлиха – Кистера.

В рамках модели жидкость рассматривается как фаза, которая может быть описана общей формулой:

(Ba²⁺, Fe³⁺, Pb²⁺) p (O^2–) q , где p и q – числа ионов (катионов и анионов, соответственно), вычисляемые по специальным формулам [15, 16].

Все расчёты выполнены исходя из предположения об общем давлении в системе равном 1 бар.

Результаты расчётов и их обсуждение

Известно, что гексагональные ферриты имеют набор изотропных модификаций – BaFe 12 O 19 , SrFe 12 O 19 , PbFe 12 O 19 . Существование твердых растворов, т. е. частичного замещения бария, например, свинцом, рассмотрено в работе [17].

В ходе собственных исследований получены данные [18], которые свидетельствуют о том, что гексаферриты бария и свинца могут образовывать непрерывный ряд твёрдых растворов. Исходя из таких представлений, рассчитана изображенная на рис. 2 фазовая диаграмма системы BaFe 12 O 19 –PbFe 12 O 19 . Для моделирования термодинамических характеристик твёрдого раствора использована подрешёточная модель, анионную подрешётку которой составляют анионы Fe 12 O 19 ^2–, а катионную подрешётку – ионы Ba²⁺ и Pb²⁺. При этом параметры, описывающие взаимодействие между катионами, принимали равными нулю.

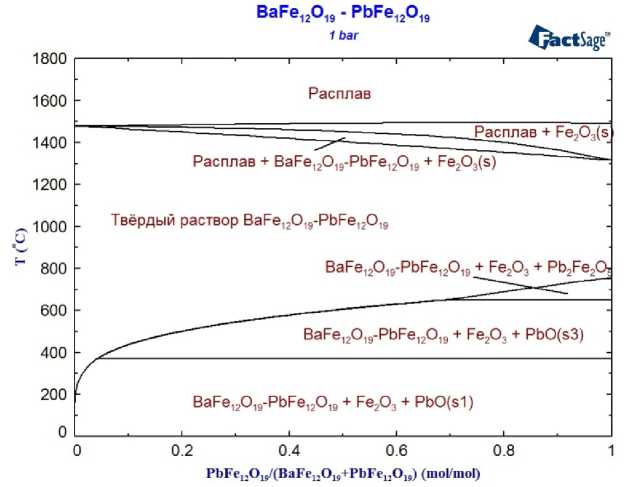
Рис. 2. Фазовая диаграмма системы BaFe 12 O 19 –PbFe 12 O 19

Кроме информации о двойных граничных системах, а также представления о твёрдых растворах в системе BaFe 12 O 19 –PbFe 12 O 19 , для моделирования фазовых равновесий в системе BaO–PbO–Fe 2 O 3 целесообразно оптимизировать параметры, характеризующие тройное взаимодействие в расплаве этой системы. На рис. 3 представлены результаты такой оптимизации в сопоставлении с полученными в ходе настоящей работы данными о температурах гомогенизации расплавов различного состава, которые и были использованы в ходе подбора значений параметров.

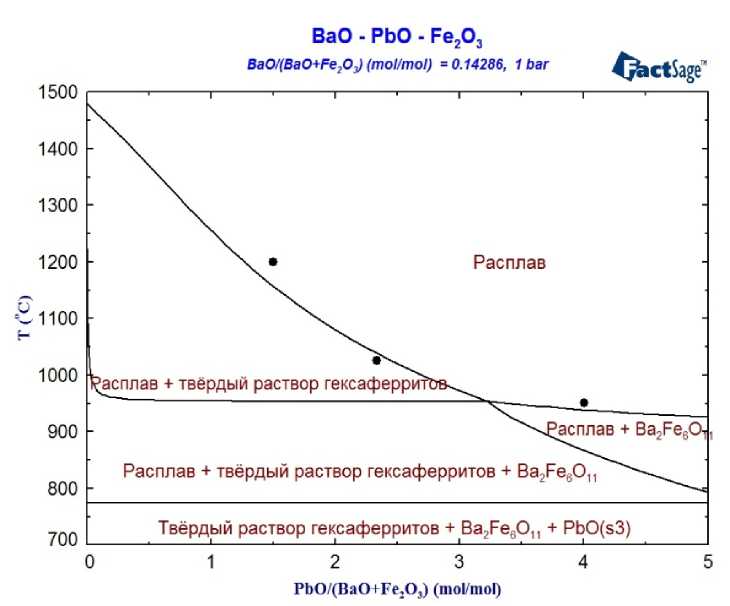
Рис. 3. Политермический разрез фазовой диаграммы системы BaO–Fe 2 O 3 –PbO на линии BaFe 12 O 19 –PbO.

Точки – экспериментальные данные работы [18] о температуре гомогенизации расплава

Набор оптимизированных параметров позволил осуществить расчёт изотермических разрезов фазовой диаграммы этой системы (рис. 4–6), а также координаты поверхности ликвидуса для этой системы, представленной на рис. 7. На последнем рисунке показано, как проходит линия разреза, соответствующего сечению BaFe 12 O 19 –PbO.

Анализ представленных результатов моделирования позволяет утверждать, что использование оксида свинца в качестве растворителя позволяет снизить минимальную температуру выращивания кристаллов гексаферрита на сечении PbO–BaFe 12 O 19 до величины порядка 960 °C и при этом использовать возможный интервал температур порядка 500 °C. То есть данный растворитель теоретически позволяет понизить нижний температурный предел проведения процесса выращивания, не снижая его верхнего значения, определённого по фазовой диаграмме системы BaO–Fe 2 O 3 . Особенностью данного растворителя, однако, является то, что образующиеся в результате кристаллы гексаферрита фактически будут представлять собою твёрдый раствор BaFe 12 O 19 –PbFe 12 O 19 (в котором, впрочем, как показывают результаты расчёта, гексаферрит бария при интересующих нас условиях будет преобладать).

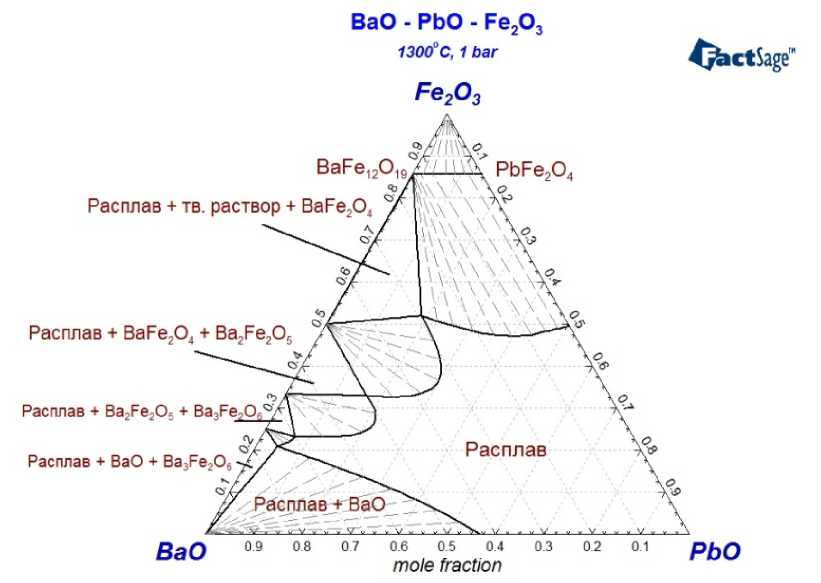
Рис. 4. Изотермический разрез фазовой диаграммы системы BaO–Fe 2 O 3 –PbO для Т = 1300 °С

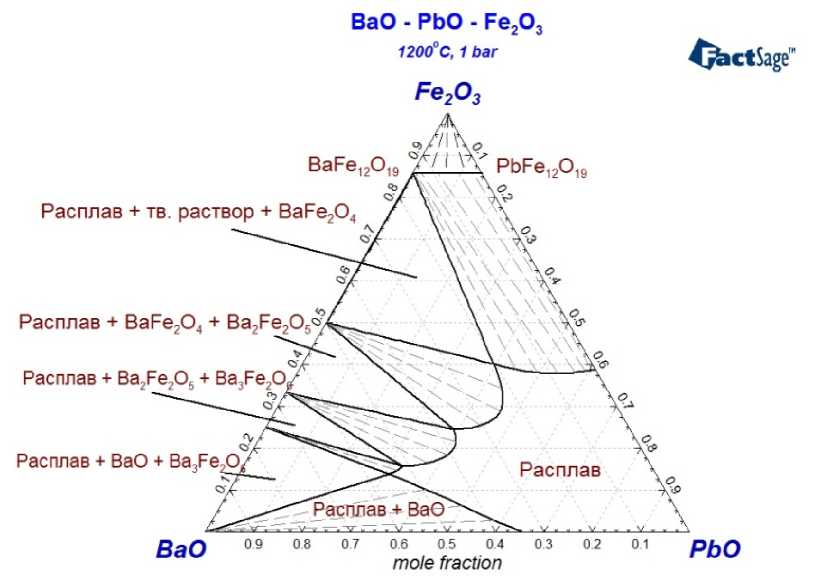
Рис. 5. Изотермический разрез фазовой диаграммы системы BaO–Fe 2 O 3 –PbO для Т = 1200 °С

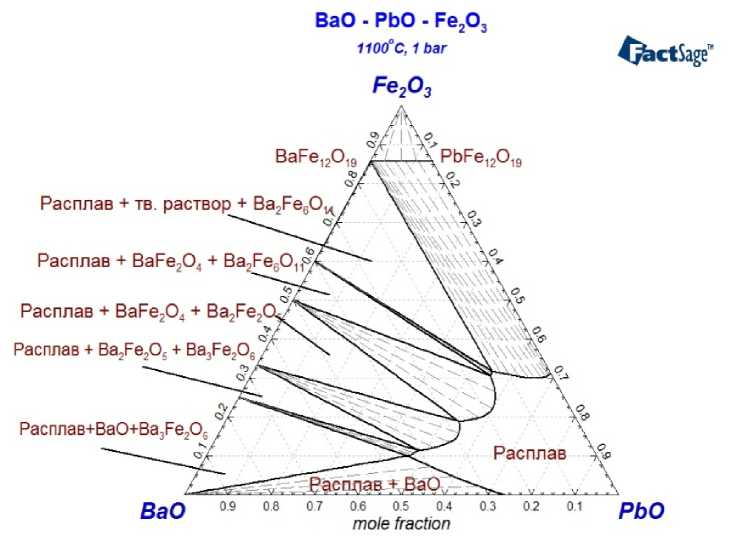
Рис. 6. Изотермический разрез фазовой диаграммы системы BaO–Fe 2 O 3 –PbO для Т = 1100 °С

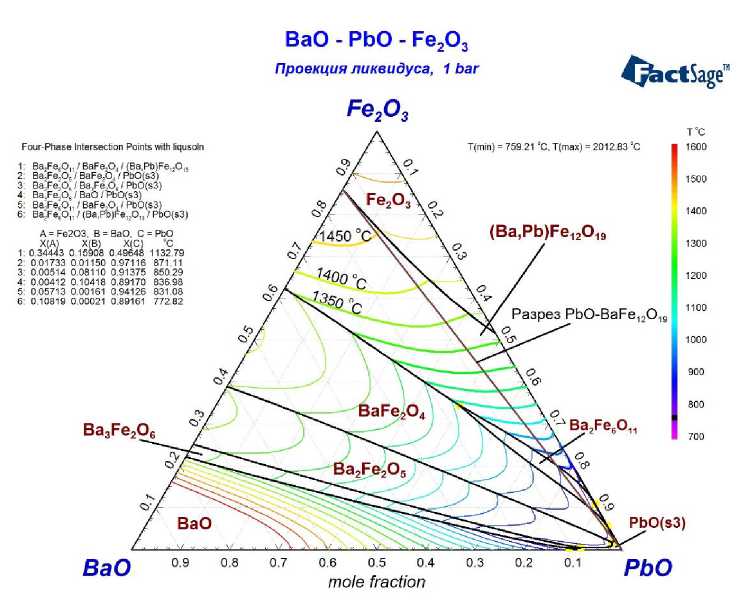
Рис. 7. Поверхность ликвидуса для фазовой диаграммы системы BaO–Fe 2 O 3 –PbO

Представление о соотношениях масс компонентов шихты, которую можно использовать для выращивания кристаллов гексаферрита, позволяет получить результаты расчёта политермическо-го разреза фазовой диаграммы системы BaO–Fe 2 O 3 –PbO на линии BaFe 12 O 19 –PbO, на которой состав системы выражен в массовых долях (рис. 8).

К сожалению, серьёзным недостатком использования такого растворителя является высокое давление его паров, о котором позволяют судить, в частности, изобары (давление выражено в барах), нанесённые на рис. 8. Это, учитывая токсичность свинца и требования к простоте конструкции оборудования для выращивания кристаллов, затрудняет использование PbO.

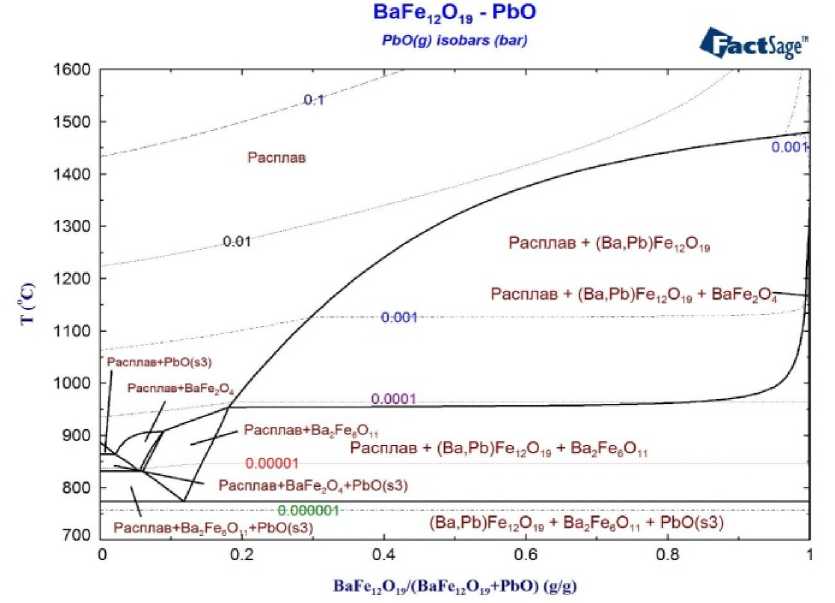
Рис. 8. Политермический разрез фазовой диаграммы системы BaO–Fe 2 O 3 –PbO на линии BaFe 12 O 19 –PbO в масс. долях. Нанесены изобары, отражающие равновесное парциальное давление PbO

Выводы

В результате проведенного исследования, опираясь на экспериментальные данные, подобраны и оптимизированы самосогласованные наборы значений термодинамических параметров, позволяющие моделировать фазовые равновесия, реализующиеся в системе BaO–PbO–Fe 2 O 3 . Сформирована пользовательская база данных, позволяющая проводить расчёты с помощью программного пакета FactSage. С помощью программного пакета FactSage рассчитана фазовая диаграмма системы BaO–PbO–Fe 2 O 3 . Результаты расчётов представлены в виде изотермических и политермических разрезов диаграммы, а также поверхности ликвидуса исследуемой системы. В необходимых случаях на диаграммы нанесены изобары, отражающие равновесные парциальные давления PbO. Анализ результатов моделирования позволяет утверждать, что использование оксида свинца в качестве растворителя позволяет снизить минимальную температуру выращивания кристаллов на сечении PbO–BaFe₁₂O₁₉ до величины порядка 960 °C и при этом использовать возможный интервал температур порядка 500 °C. Полученные результаты будут востребованы для рационального выбора режимов выращивания кристаллов гексагональных ферритов из раствора (флюса).

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 16-08-01043_А), а также правительства Российской Федерации (постановление № 211 от 16.03.2013 г.), соглашение №02.A03.21.0011.