Фазовая проблема и синтез оптических полей

•♦      1           .     1 [ dl где (rocj)^-^-(vixvy)             ay ” ay dx J *

При этом в изолированных нулях интенсивности имеет место соотношение

При распространении поля в зоне Френеля изолированные нули образуются парами с противоположными знаками (rot j)t в них. Численные эксперименты показали, что, во-первых, проблема восстановления полей по интенсивности связана с вихревыми свойствами векторного поля j, во-вторых, информация о знаке и модуле (rot j) в изолированных нулях интенсивности определяет в основном структуру поля и обеспечивает устойчивое восстановление векторного поля j.

К настоящему времени в общем случае не решен вопрос определения знаков (rot j)f в изолированных нулях. Используя аппарат теории функций комплексной переменной, удается лишь разделить нули по парам с противоположными знаками (rot j) .

Для задачи синтеза эта неопределенность означает, что могут существовать близкие (или равные) по интенсивности поля, обладающие существенно различной структурой, и пренебрежение соотношениями типа ( 1) при постановке задачи может привести к тому, что соотношение (1) все же реализуется, но при этом результат синтеза может отличаться от исходно заданного.

Например, соотношение (1) «запрещает» отдельные варианты изменения интенсивности при распространении поля: покажем, что невырожденный минимум интенсивности не может стать невырожденным нулем (см. рис. 16. Невырожденность нуля здесь понимается в смысле невырожденности для функции F(x, у), то есть F(x, у) = О, но VF(х, у) * 0). Рассмотрим область

Плоскость (х.у)

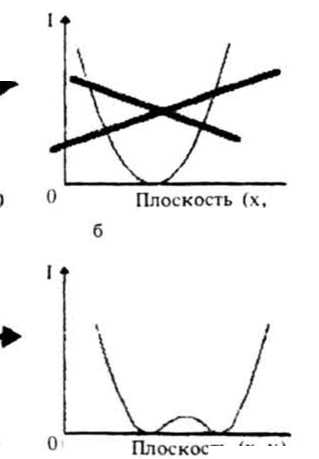
Рис. 1. Невозможный (б) и возможный (в, г) варианты реализации невырожденного нуля из локального минимума интенсивности (а) при распространении поля вдоль 1

Q = |(x, y)gR², I(x, y) < I_Q = constj-, содержащую точку минимума (семейство таких областей всегда существует). Используя соотношение (1), получим

jlVydr=lJvpdr=^ = О

5Q        SQ Q

Так как (rot j)i - вещественная непрерывная по х, у, 1 функция, то существует кривая в области Q, на которой (rot j) равен нулю и которая в •*                 1                             1

силу соотношения (rot =  —^- (V I х V ф)[ проходит через точку минимума. Пусть при распространении поля при некотором 1 интенсивность в минимуме достигает нулевого значения. В силу непрерывности (rot j)1 линия нулевого ротора должна проходить через этот глобальный минимум. С другой стороны, в невырожденном нуле интенсивности (rot j)j в соответствии с (2) имеет конечное ненулевое значение. Следовательно, это вырожденный нуль (рис. 1в). При малом возмущении он распадается на пару невырожденных нулей с конечными значениями ротора, разделенных нулевой линией (rot j) . Поэтому ротор в этих нулях имеет противоположные знаки (рис. 1г).

В качестве примера учета вихревой составляющей при синтезе световых полей рассмотрим задачу фокусировки лазерного излучения в кольцо радиуса

г на расстоянии f .

о г                 о

В параксиальном приближении известным решением, полученным по методу стационарной фазы [2], является фокусатор «сферическая линза + аксикон>:

<ро(г)

, 2.

krкгг

----+----

2ff оо

Легко видеть.

что данное решение в приближении геометрической

оптики реализует отображение

( £, Л) -> (х, у) с нулевым якобианом:

y=71+f0	Л --4-	го	Л	- г sin а
	f 1 О	f 0	/ „2, 2 v С +л	0

Соответствующее дифракционное поле Фокальной плоскости имеет вид:

обладает нулевым ротором и в

FO(P)-

kEo Г ikp2

---exp ikf +---- if          ° 2f о                     о

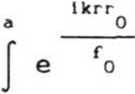
r j Jo

kp ---- r dr,

где

E_q - амплитуда светового поля в плоскости (£,

л) ;

Р - полярный радиус;

а - радиус фокусатора.

График зависимости IQ(p) - |FQ(p)|2 от полярного радиуса р приведен на рис. 2 (п-0). Появление локального максимума интенсивности в центре обусловлено различием между геометрооптическим приближением и его волновой реализацией. Из вышесказанного ясно, что устойчивая нулевая интенсивность в центре может существовать лишь при нулевом роторе.

Простейшими решениями

фокусировки в кольцо с ненулевым ротором являются решения вида кг2 кгго

Ф (г, а)---+------+па,

"           2f f о о где п - целое число, а - arg(£+i,T)).

При

F (р, п

этом дифракционное поле Ffi(p,

в) примет вид

кЕо            ikp2

в) - ----exp ikf +---- +ine + if          ° 2f о                    о

3nin

1кгг а _____О

J е f° rj_

о

кр

г dr. (8)

Особенность при г - О не играет существенной область (г, а) € [с, а]х[О, 2л], где с<<а.

Графики зависимости 1п(р) ■ lFn(P) |2 от Р Для п ■

роли: можно взять

1, 2, 3 показаны на

рис. 2.

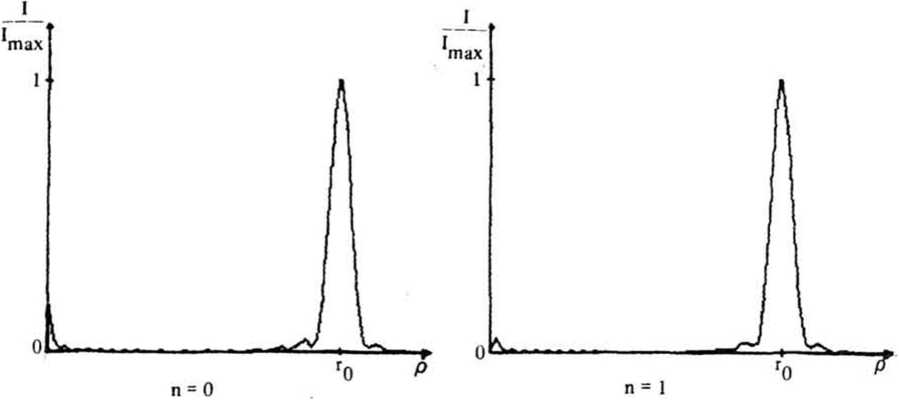
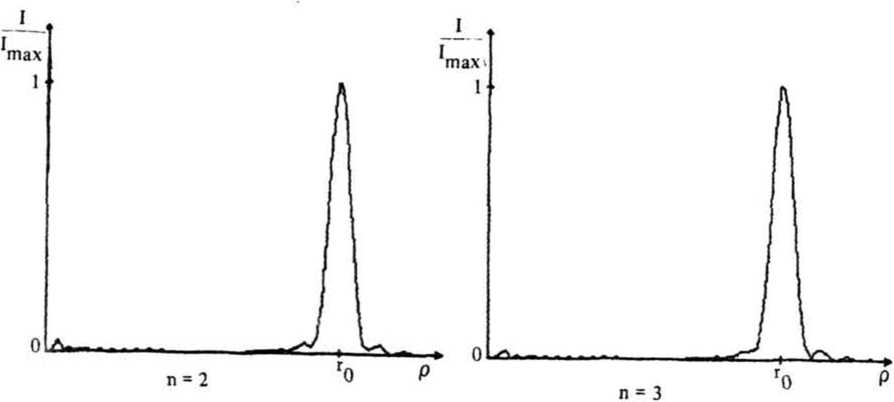
Рис. 2. Зависимость интенсивности от полярного радиуса для фаз, вычисляемых по формуле (7), при различных п

Если обратиться к аналогии между поведением жидкости и распространением энергии светового поля, то решения (7) и (4) соотносятся так же, как два способа создать воронку на поверхности жидкости: вращением и центрально-симметричным давлением на нее.

Фокусатор (7) реализует взаимно однозначное (при г*0) отображение с ненулевым якобианом:

nf x-r cos 9---sin е, кг nf                                      (9)

у-г sin е+----cos 6. о , кг

Однозначность отображения (9) означает, что фокусатор (7) не производит фокусировки в смысле метода стационарной фазы. Более того, положение максимума интенсивности г^ приходится на область 2,2 n f

Го+--2~2"^Т0 обусловлено тем» что решения (7) являются волновыми и не могут быть получены в рамках геометрической оптики.

Соответствующая дискретная задача при конечном числе N градаций фазы ф^(г, а) дает осцилляции интенсивности в области кольца. Например, при N=6 осцилляции не превышают 13%. На рисунках 3, 4 показаны сечения поверхностей интенсивности для шестиградационной фазы при п - 0, 1 и распределение 1_} (р, 6) на окружности, где достигается максимальная интенсивность.

Решения типа (7) легко обобщаются на ряд задач фокусировки в кривую (например, эллипс). Авторами разработаны несколько подходов к решению задач фокусировки в произвольные область и кривую.

б а

Рис. 3. Сечения профилей интенсивности при шести градациях фазы в безвихревом (а) и вихревом (б) случаях

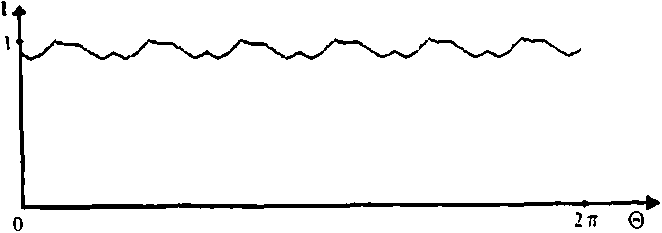
Рис. 4. Зависимость интенсивности от полярного угла на кольце максимальной интенсивности