Фазовые дифракционные оптические элементы для одновременного формирования мод Гаусса-Лагерра в различных дифракционных порядках

Моды определяются как устойчивые при распространении в волноводной среде световые пучки. Моды не расплываются и не изменяют пространственной структуры в процессе распространения в своей среде, а лишь приобретают фазовый набег [1].

Рассматриваемые моды Гаусса-Лагерра сохраняют также свою структуру и в свободном пространстве, изменяясь лишь масштабно.

Актуальной задачей является создание приборов, формирующих эталоны модовых пучков, и приборов, измеряющих модовый состав лазерных пучков. Такие приборы смогут осуществить индивидуальное возбуждение, измерение и обнаружение мод когерентного излучения.

В работах [1-3] в качестве таких приборов рассматриваются дифракционные оптические элементы (ДОЭ), рассчитанные с помощью разных методов. Особый интерес представляют фазовые ДОЭ, имеющие повышенную энергетическую эффективность и многоканальный характер работы, позволяющий сформировать несколько модовых пучков. Такие ДОЭ можно использовать для параллельного ввода излучения в набор волокон или для оптического разложения когерентного поля по ортогональному базису.

Для расчета многоканальных ДОЭ, согласованных с модами Гаусса-Лагерра, в данной работе используется итерационный метод аппроксимации фазовой функции пропускания ДОЭ конечной суммой гауссовых мод [4].

Рассчитанные 9- и 24-канальные 64-градационные ДОЭ были изготовлены в Университете Йоенсуу методом прямой записи электронным пучком на стекле.

В данной работе впервые экспериментально продемонстрирована возможность одновременной генерации набора различных модовых пучков (более 8 пучков), распространяющихся под разными углами к оптической оси.

1.    Теоретическая основа

Данные элементы применяются как пространственные фильтры для анализа поперечного модового состава света и для одновременного ввода света в набор волокон [1].

Если ДОЭ, у которого функция пропускания представлена в виде линейной комбинации ограниченного числа базисных функций {ψ nm (x,y) }с различными несущими пространственными частотами:

NM

^{т (} x , У ) = E E ^ nm ⁽ x , y ) exP ^{[ i (a} nm x + Р пт У ^)] , (1) n = 0 m = 0

совмещен со сферической линзой и освещен световой волной W(x,y), то интенсивность света в заданных точках фокальной плоскости с пространственными частотами (α nm , β nm ) будет приближенно пропорциональна квадратам модулей коэффициентов разложения w_nm светового поля по этому базису:

NM

W ( x , У ) = EE w nm V nm ^{( x} , У ) .               ⁽²⁾

n = 0 m = 0

Эта пропорциональность будет тем точнее, чем больше разность соседних пространственных несущих частот:   ^nm - “pq I >> 1, l^nm - в pq | >> 1, n * p, m * q , то есть, чем больше будут разделены между собой в пространстве отдельные моды.

Рассмотрим метод расчета оптических элементов, формирующих высокоэффективные моды Гаус-са-Лагерра в заданных дифракционных порядках с требуемым распределением энергии света между модами.

Пусть требуется вычислить фазу оптического элемента S(x,y) , который образует (будучи освещенным плоским пучком света с амплитудой A 0 (x,y) ) моды Гаусса-Лагерра в дифракционных порядках, определенных векторами несущих пространственных частот (α nm , β nm ), характеризующих наклон к оси распространения пучка с номерами (n,m) . Комплексная функция пропускания такого элемента должна удовлетворять в полярных координатах соотношению:

A 0 ( r , Ф ) exp [ «5 ( r , Ф ) ] =

N

= E E Cnm ^nm (r, Ф) x ,

n=0|m| < n x exp[- irPnm cosOp - 9nm )]

где ^ _nm ( r, ф ) - обобщенная функция Лагерра:

²V ⁿ ( ⁿ -I m l) ( 2rr ) m'

^nm (r, Ф )=             I ---- I x

a ^( n ! ) 3 I ^CT 0 )

Гаусса-

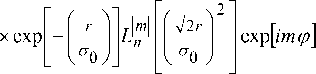
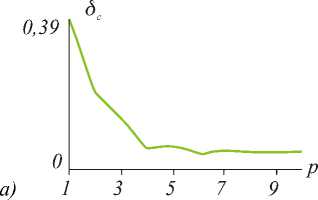
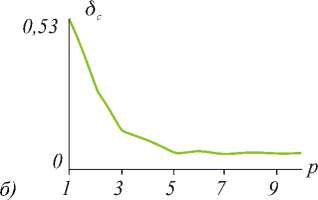
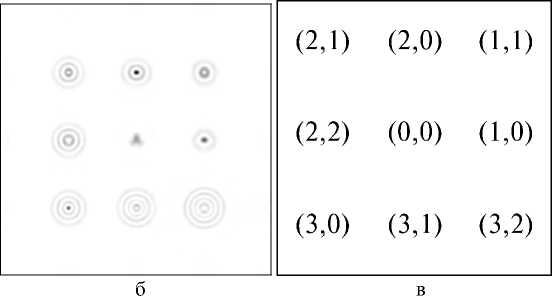
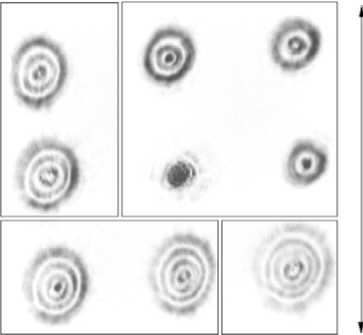
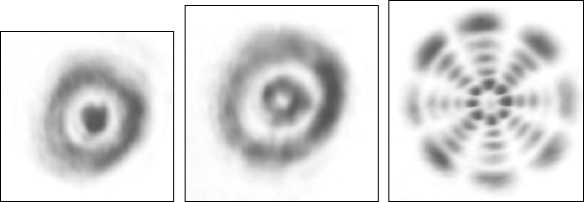
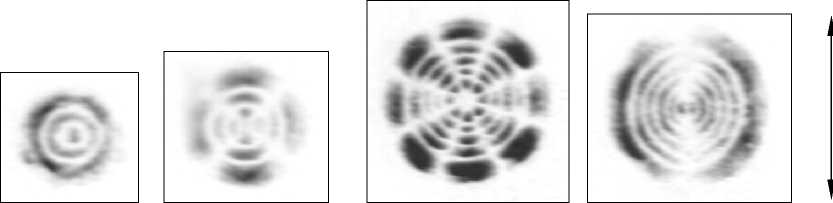
222    y r = x + y ,   ф = arctg— , n>0, |ml

x dm

Lm (x) = (-1) m—m [Lm+n (x)] - обобщенный много член Лагерра, сто - радиус перетяжки. Квадраты модулей коэффициентов Cnm характеризуют энер- гетический вклад каждой моды, а аргументы Cnm являются свободными параметрами задачи, (ρnm, 9nm) - вектор несущих пространственных частот в полярных координатах.

При достаточно большой разнице между соседними векторами пространственных частот

®n, m; n+1, m +1 ^pn, m^{+ p}n+1, m +1

,         ,                 ,                ,(5)

^{- 2 p}n,m Pn+1,m +1 cos⁽⁹n, m ⁹n+1, m+1)

можно считать, что пучки пространственно разделяются в Фурье-плоскости и функции

Ynm (r, Ф) exP[- irPnm cosGP " 9nm )]

почти ортогональны. Тогда коэффициенты в (3) можно вычислять по формуле:

да 2n

Cnm = J J A0 ⁽r, Ф) exP^⁽r, Ф^)]^*m⁽r, ф) x

x exp[irp_nm cos(ф - 9_nm)]rdrdф

Далее для расчета ДОЭ с фазой S(r,ϕ) применяется итеративный алгоритм, описанный в [4].

Функции Гаусса-Лагерра являются собственными функциями преобразования Фурье:

1 2п да

— J ( ^nm^(r, Ф^)exP^[-irP^coS⁽Ф " ^9)]x

²ⁿ 0 0                                   ,        (8)

^xr^dГ^dф = ^(-1)^{n (-}i)^m Ynm⁽P, 9)

что позволяет использовать их для эффективного ввода излучения в световые волокна [1].

Заметим, что функции Гаусса-Лагерра со взаимно противоположной «закруткой» exp[±i|m|ϕ] имеют одинаковые собственные значения:

^nm = (-1) n С"i) m¹ .                                 (9)

Совокупность мод Гаусса-Лагерра с одинаковыми собственными значениями можно считать “модовой группой”, так как она также представляет собой собственную функцию преобразования Фурье.

• 2.    Численное моделирование

При численном моделировании использовались следующие параметры: 256 отсчетов по радиусу r и 256 отсчетов по угловой составляющей θ, диапазон изменения аргументов r∈[0,7мм], θ∈[0,2π], длина волны λ=0.63 мкм, фокусное расстояние f=100 мм, радиус гауссового пучка в перетяжке a=1 мм. В формуле (3.3) рассматривались члены ряда с номерами n,m ≤ N=7. Модули всех коэффициентов выбирались равными: Cnm =const.

В качестве освещающего пучка A0(r,9) выби- рались плоский и гауссовый. В Таблице 1 приведены результаты численного моделирования для 9канального и 24-канального ДОЭ для следующих параметров, характеризующих качество работы ДОЭ:

5с - относительное среднеквадратичное отклонение рассчитанных коэффициентов от заданных;

• 5 - относительное среднеквадратичное отклонение распределения рассчитанной амплитуды E_r (ξ, η) в Фурье-плоскости от идеальной E₀(ξ,η):

5 =

JJ (Er (^, п )| - E 0(^, П )|)2 d ^ d n x ^

x JJ |E0(^,n)|² d^ dп _п

где Ω - область в Фурье-плоскости, в которой за- ключено 99% энергии идеальной дифракционной картины; п - коэффициент корреляции:

Г R 2п""

п = Е ICnm|² J J A 0^{( r ,9}) r^dr^{d 9}

n, meQ       _ 0 0

где Q – множество заданных (полезных) коэффициентов.

Из Таблицы 1 видно, что освещение гауссовым пучком предпочтительней, чем плоским. Увеличение количества мод в фильтре почти в 3 раза приводит к увеличению относительного отклонения сформированных мод от идеальных не более, чем на 12%. Несмотря на высокую ошибку 5 в Таблице 1, поперечная структура рассчитанных пучков совпадает со структурой идеальных мод, отличие же заключено в перераспределении энергии внутри этой структуры. Коэффициент корреляции п показывает, что данные пучки будут возбуждать соответствующие моды со средней эффективностью более 70%.

На рис. 1 представлены графики зависимости среднеквадратичной ошибки 5с от числа итераций p для 9-канального (a) и 24-канального (б) фильтров, соответственно. Видно, что в обоих случаях после 5-6 итераций наступает эффект стагнации.

Таблица 1. Результаты численного моделирования для 9- и 24-канального ДОЭ.

Число каналов	Освещающий пучок	Радиус апертуры, R (mm) / Радиус осв. пучка Rg (mm)	Ошибка, 5с (%)	Ошибка, 5 (%)	Коэффициент корреляции, п (%)
9	плоский	3.5 / 3.5	6.3	41.2	76.3
9	гауссовый	6.0 / 3.0	4.6	31.3	76.5
24	гауссовый	6.5 / 4.0	5.4	43.1	73.7

Рис. 1. Графики сходимости после 10 итераций для 9-канального (a) и 24-канального (б) фильтров, соответственно

На рис. 2 и 3 показаны результаты численного моделирования работы рассчитанных 9- и 24канального фильтров, соответственно: (а) фаза ДОЭ,

• (б)    распределение интенсивности в Фурье-плоскости, (в) схема, показывающая расположение номеров мод по порядкам.

  

  а

  
  
  

  Рис. 2. Численное моделирование работы 9-канального фильтра при освещении гауссовым пучком: (а) фаза ДОЭ, (б) распределение интенсивности в Фурье-плоскости, (в) схема, показывающая расположение номеров мод по порядкам.

  
  
  

  а                               б                               в

  Рис. 3. Численное моделирование работы 24-канального фильтра при освещении гауссовым пучком: (а) фаза ДОЭ, (б) распределение интенсивности в Фурье-плоскости, (в) схема, показывающая расположение номеров мод по порядкам.

  
  
3.    Изготовление многоуровневых ДОЭ. 4.    Эксперимент

Для изготовления многоуровневых элементов в Университете Йоенсуу (Финляндия) были использованы новый низкоконтрастный негативный электроннолучевой резист X AR-N 7700 фирмы AllResist GMbH (Берлин), электронно-лучевой генератор изображений Leica LION LV1 и реактивное ионное травление.

Резист был нанесен на кварцевую подложку толщиной 1100 нм и затем подложка подвергалась термической обработке при температуре 85°C в течение 30 мин. в воздушно-циркулярной печи. Алюминиевый слой толщиной 20 нм наносился на подложку. Формирование изображения на резисте выполнялось с помощью электронно-лучевого генератора изображений Leica LION LV1 при уско- ряющем напряжении 12.5 кВ. После экспозиции алюминиевый слой был удален раствором гидро-хлорной кислоты и деионизированной воды. Затем подложка подвергалась чередующейся термической обработке в воздушно-циркулярной печи (30 мин. при 110°C и 4 часа при 70°C ). Проявление было выполнено за 50 сек. с помощью проявляющего раствора AR 300-47/деионизированная вода (2/1). Для переноса профиля резиста на SiO2 было использовано пропорциональное реактивно-ионное травление в CHF3.

Существенного загрязнения в результате повторного осаждения продуктов травления не наблюдалось и желаемая глубина профиля может быть получена обычным способом с точностью 30 нм (не хуже 2.5%).

На рис. 4 приведен пример профиля дифракционной поверхности, полученного в результате экспозиции в резисте X AR-N 7700 и пропорционального травления в SiO2. Элемент имеет 16 уровней и размер пиксела 2.5 мкм х 2.5 мкм.

Рис. 4. Пример 16-уровневого профиля дифракционной поверхности, полученного в результате экспозиции в резисте X AR-N 7700 и пропорционального травления в SiO2.

Для проверки ДОЭ формирующих пучки Гаус-са-Лагерра в различных дифракционных порядках был проведен ряд натурных экспериментов. Оптическая схема экспериментальной установки приведена на рис. 5. Здесь L - He-Ne лазер, K – коллиматор, F - ДОЭ, L1 – первая линза, D - диафрагма, L2 – вторая линза, TV - телекамера, PC - компьютер.

С помощью коллиматора K формируется плоский пучок, который попадает на ДОЭ – F. После ДОЭ в Фурье-плоскости первой линзы формируется набор пространственно разделенных мод. Диафрагма D вырезает из набора одну моду, затем вторая линза формирует ее Фурье-образ, который вводится в компьютер через телекамеру. В ходе экспе- набора мод в плоскости диафрагмы. Для этого убиралась часть оптической схемы, которая обведена пунктирной линией.

Рис. 5. Оптическая схема экспериментальной установки.

На рис. 6 показаны экспериментальные результаты по формированию 9-ти мод Гаусса-Лагерра с номерами (n,m): (0,0), (1,0), (1,1), (2,0), (2,1), (2,2), (3,0), (3,1), (3,2) в различных дифракционных порядках.

Рис. 6. Экспериментально зарегистрированное распределение интенсивности в фокальной плоскости линзы для 9-канального фильтра (для лучшей видимости составлено из фрагментов).

На рис. 7а,в,д,ж показаны более крупным планом экспериментально зарегистрированные порядки, соответствующие модам (1,0), (1,1), (2,1), (3,0), а на рис. 7б,г,е,з приведены их Фурье-спектры. Видно, что сформированные пучки сохраняют свою структуру, проявляя модовый характер.

римента также осуществлялась регистрация всего

a                  в                       д

б                   г                         е

Рис. 7. Дифракционные порядки, соответствующие модам (1,0) (a), (1,1) (в), (2,1) (д), (3,0) (ж) в 9-канальном фильтре, и их Фурье-спектры (б, г, е, з).

На рис. 8 показаны результаты по формированию 24-х модовых пучков Гаусса-Лагерра, представляющих собой групповые моды, инвариантные к преобразованию Фурье, с номерами (n,±m): (0,0), (1,0), (1,1)+(1,-1), (2,0), (2,1)+(2,-1), (2,2)+(2,-2), (3,0), (3,1)+(3,-1), (3,2)+(3,-2), (3,3)+(3,-3), (4,0), (4,1)+(4,-1), (4,2)+(4,-2), (4,3)+(4,-3), (4,4)+(4,-4), (5,0), (5,1)+(5,-1), (5,2)+(5,-2), (5,3)+(5,-3), (5,4)+(5,4), (5,5)+(5,-5), (6,0), (6,1)+(6,-1), (6,2)+(6,-2) в различных дифракционных порядках.

На рис. 9а,в,д,ж показаны более крупным планом экспериментально зарегистрированные порядки, соответствующие композициям мод (2,0), (2,2)+(2,2), (4,4)+(4,-4), (5,1)+(5,-1), а на рис. 6б,г,е,з приведены их Фурье-спектры. Видно, что сформированные пучки сохраняют свою структуру, проявляя модовый характер.

Рис. 8. Экспериментально зарегистрированное распределение интенсивности в фокальной плоскости линзы для 24-канального фильтра.

a               в                    д                  ж

б

Рис. 9. Дифракционные порядки, соответствующие пучкам (2,0) (a), (2,2)+(2,-2) (в), (4,4)+(4,-4) (д), (5,1)+(5,-1) (ж) в 24-канальном фильтре, и их Фурье-спектры (б, г, е, з).

Заключение

В данной работе получены следующие результаты:

• •    рассчитаны и изготовлены методом прямой записи электронным пучком на стекле фазовые 64-градационные ДОЭ, формирующие с эффективностью около 90% одновременно 9 и 24 разных пучков Гаусса-Лагерра, распространяющихся под заданными углами к оптической оси;

• •    экспериментально показано, что пучки сохраняют свою структуру в Фурье-плоскости (в дальней зоне), то есть действительно являются модами свободного пространства.

Данная работа поддержана Российским фондом фундаментальных исследований (№98-01-00894, 9901-39012).