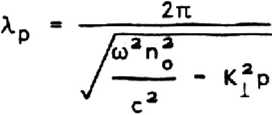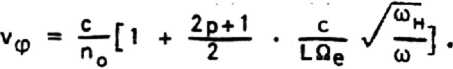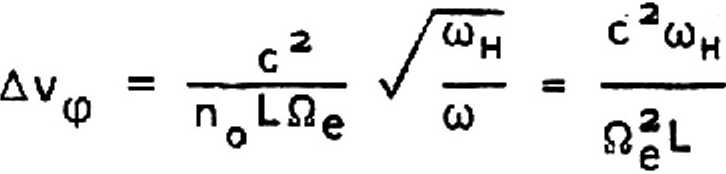Фазовые эффекты в диагностике ионосферных плазменных волноводов
Автор: Багбая И.Д.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Волноводы. Световоды
Статья в выпуске: 6, 1989 года.
Бесплатный доступ
Рассматривается специфика фазовых эффектов в волноводных плазменных системах. Показываются возможности плазменной диагностики в таких системах, отличающихся от неограниченных плазменных объемов модовой структурой волнового поля. Отмечаются перспективы применения эффектов межмодовой дисперсии для определения интегральных характеристик плазменных неоднородностей.
Короткий адрес: https://sciup.org/14058190
IDR: 14058190
Текст научной статьи Фазовые эффекты в диагностике ионосферных плазменных волноводов
-
е1±9 A-iB'
А = -[i(vei + vem)±wH] (co±nH-iVim);
В = -(Vp. - ------- тг-ИПн + 1Ует с 1 со где
Ne и Мт - плотность электронов и нейтральных молекул;
vej и vem ~ частоты электрон-ионных и электрон-молекулярных столкновений; v^m - частота ион-молекулярных столкновений;
fle и Йн " гирочастоты электронов и ионов;
Пе - плазменная частота;
m и М - массы электрона и поля.
Рассмотрим теперь некоторые области локализации низкочастотных электромаг нитных волн в регулярной ионосфере.
НИЗКОЧАСТОТНАЯ ВОЛНОВОДНАЯ ПОЛОСТЬ В F-СЛОЕ
В интересующей нас области высот 2^300 км значения параметра Ne*N^1 малы -NeeNm1$1О-3. При этом в ионном составе плазмы основную роль играет ион 0 + , так что отношение масс m-М-1 составляет 3,^*10_3, а гирочастота Ян меняется от Пм—1^0 рад»с~1 на экваторе до Ян»70 рад*с"1в полярных районах.
Компонента ец имеет вид
Ле еИ " 1 " w(co-ive) ; ve=vei+vem'
где параметр Я3 вблизи максимума F-слоя на высоте ZQ оценивается величиной Ле»5*Ю13 (рад*с"1)а в дневных условиях (Zo=300 км) и величиной я|=1015
(рад ■с-1)3 - в ночных (Zo=400 км). Частоты столкновений в этой области Ves800 с”1;
v^ms1,5 с-1 днем и ve=270 с”1, v^ms0,1 с-1 ночью.
Вычисления по формулам (2)-(3) показывают.
что в области частот оу«сон ком
поненты ej и g имеют пе°н [ е 2 = ---------------< 1
“н(^2)
шЯа
9 = ------------- <1
toH(to3-Qa)
ВИД
inH
to
^e
CD
H
2^1m°H to3-Q3
ivimto3-Ffl3 ive ш+Ян
4. —------ + —— . . ■■ ,—■ to(to3-toj) WH to-fiH
toCto3+G3)
Ян(to+Rи)3
Как видно из (4)-(6)z в диапазоне частот 2*103 рад*с-1
I е± ец I»I е^ I ; I е± е ц I»I g I а (7) эти неравенства дают возможность упростить общее выражение (1) для показателя преломления в широкой области углов, удовлетворяющих условию:
tgaa»|— | . е||
При соблюдении условий (7)-(8) выражение (1) примет вид е। (2-si nа a)± V ef«sfn4 a+4g3cosaa
( n - i х)3 = -------------------------------------------------------- .
2cos3 a
Здесь, в отличие от (1), знак "+" соответствует необыкновенной волне, знак u-u - обыкновенной.
Следует отметить, что выражения для Re^^ и Re9 (5)—(6) меняют знак при переходе через точку to=RH . Поэтому целесообразно рассмотреть дисперсионные свойства обсуждаемых волн в диапазонах ш>Ян и оуСЯн по отдельности.
Диапазон щ>Ян
Этот диапазон в условиях (7)-(8) непрозрачен для волн обыкновенной поляризации почти во всем створе углов 0<а< ^, однако необыкновенные волны могут распространяться здесь, причем показатель преломления, как видно из рис. 1, мало изменяется в широком створе углов а вокруг направления магнитного поля Н. Существенно, что с уменьшением частоты со (однако в пределах со<Ян) этот угол растет; так, при ш=150 рад-с-1 при изменении угла а от аш0 до а-6О° показатель преломления возрастает лишь до Дн*п~1=0.3.
В частном случае co>>QH выражение (9) переходит в известную формулу [2]
(n-ix)3 - --- . (10)
cos а
При дальнейшем росте угла а в рассматриваемом диапазоне частот может возникнуть область непрозрачности для необыкновенных волн (п3<0) . Однако при квазипоперечном распространении (а-» ^ г когда условие (8) нарушено, для необыкновенных волн вновь возникает область прозрачности, отличающаяся высокими значениями по казателя преломления (п£103) (рис. 2)
П3
п2--2- , <”> где Пр - нижняя гибридная частота.
Яр = toH^Y^nj- (12>
j
Суммирование *в (12) ведется по всем сортам ионов, Yj * доля ионов сорта j в ионном составе плазмы; в области максимума слоя F частота Пр меняется от Пр-2,3*10* рад-с"1 на экваторе до Ор-1,6-10* рад-с-1 вблизи полюсов. Для волн с частотой cos(5-10)■103 рад-с-1 такая волноводная область соответствует углам а=87-90°.
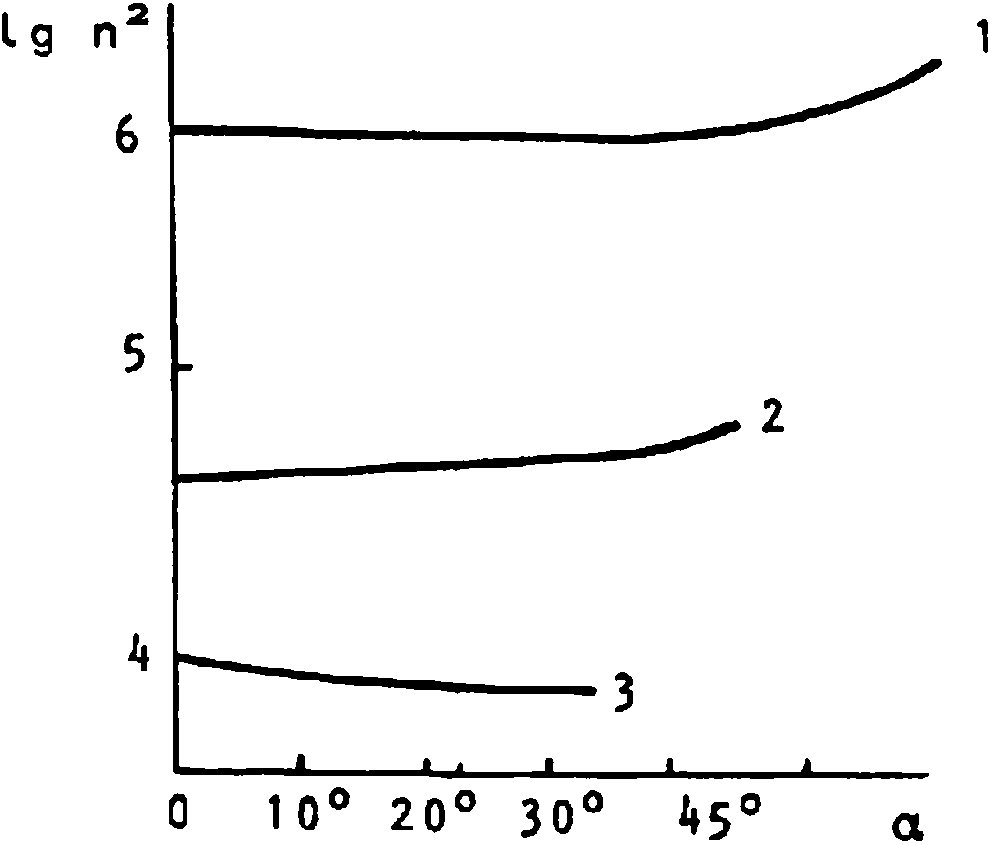
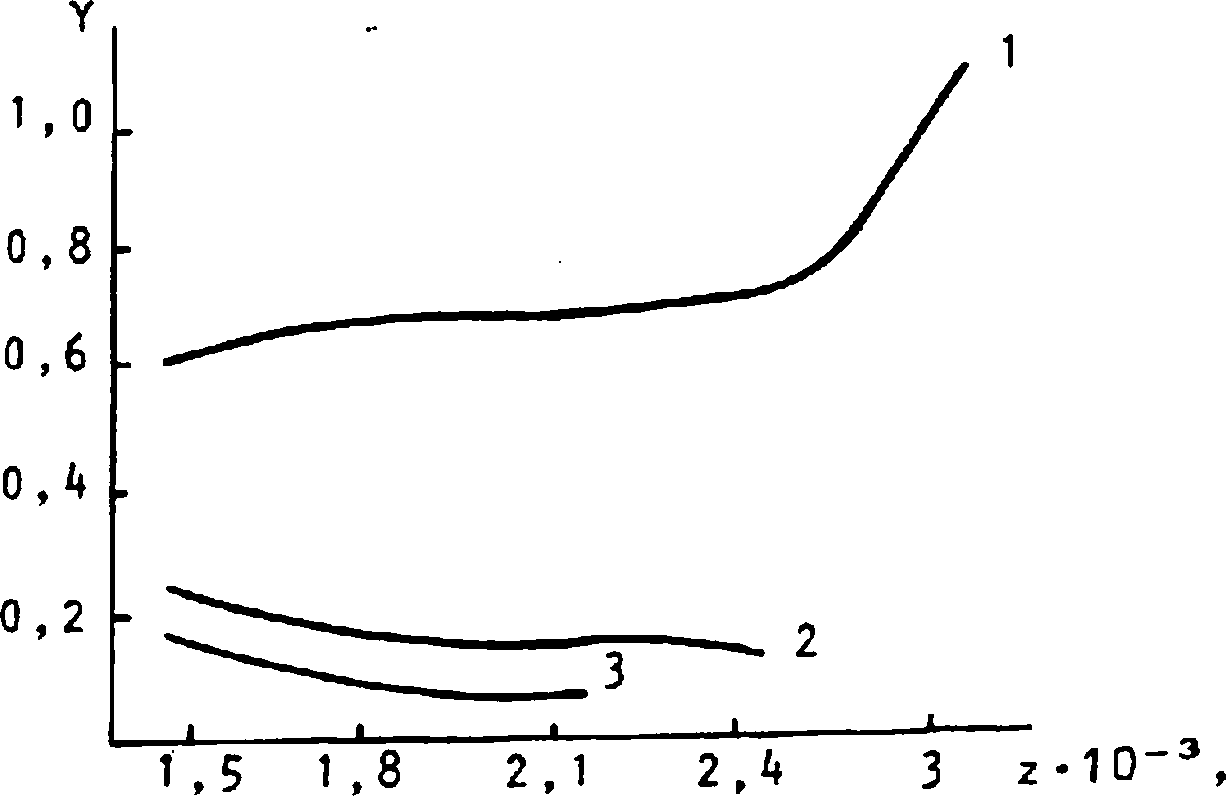
Рис. 1. Зависимость показателя преломления необыкновенной волны _ п от угла а между волновым вектором К и магнитным полем Н вблизи максимума
F-слоя: кривые 1, 2 и 3 соответствуют частотам со-150, со=2«103 и со«3-10й рад-с"1
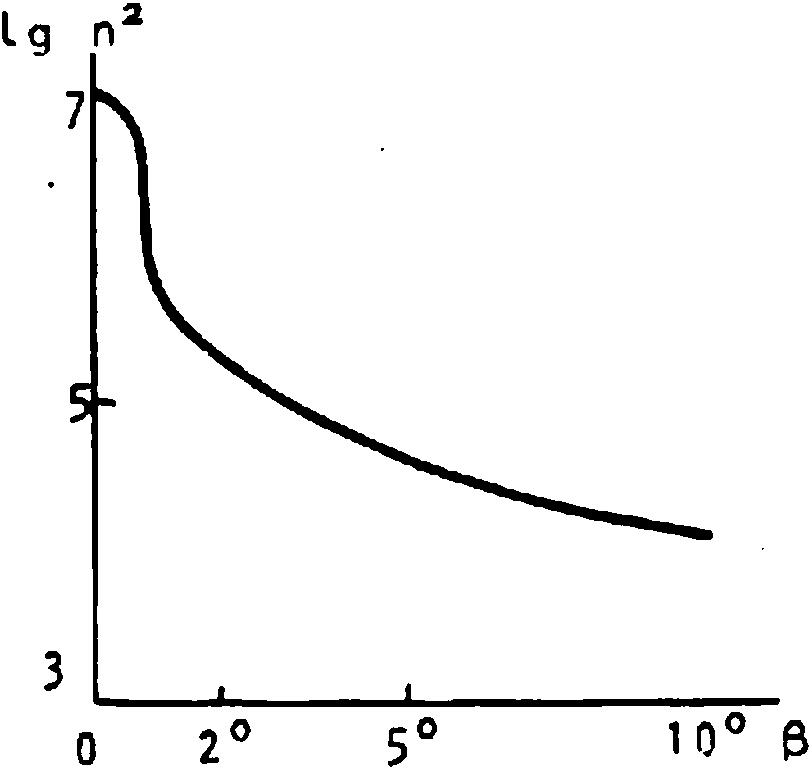
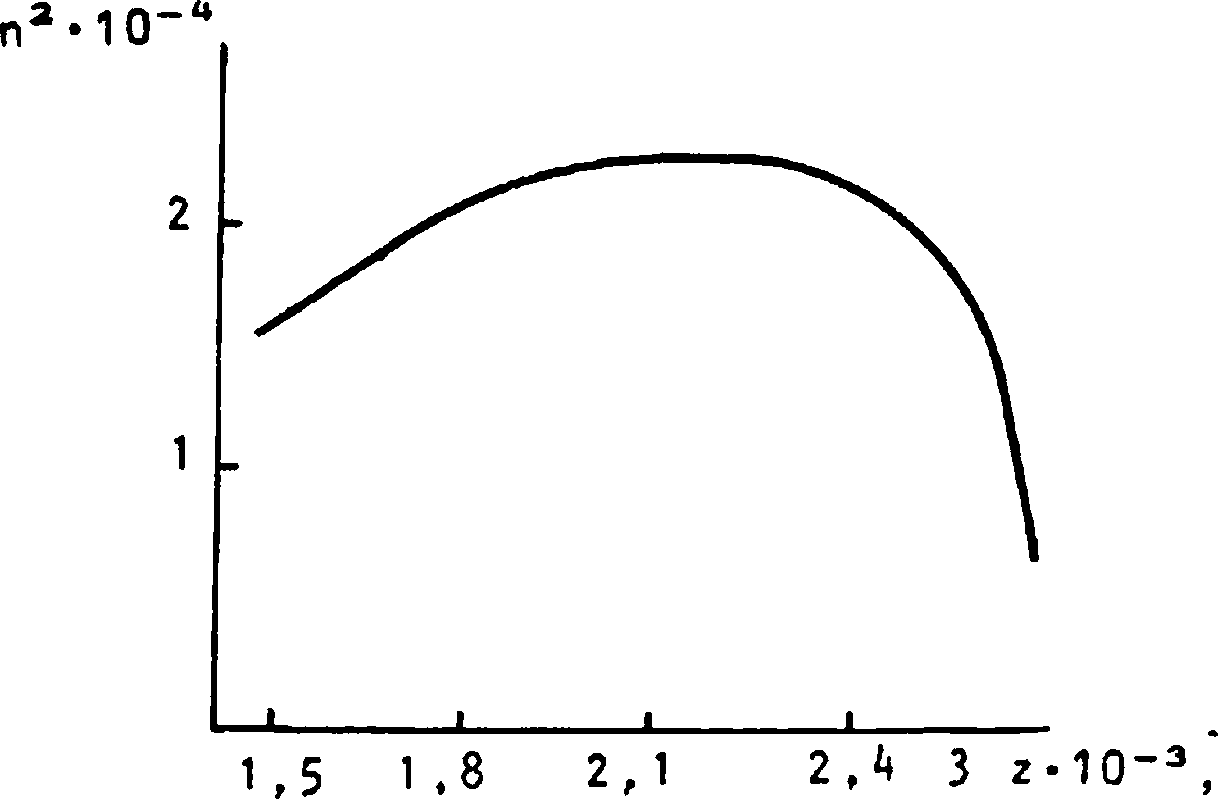
Рис. 2. Угловая зависимость показателя преломления необыкновенной волны при квази поперечном распространении (Р=90°-а) в Г-слое ионосферы в низких широтах (ш=4п-103 рад-с"1)
Как видно из выражения для параметра g (6), условие |E1E|il»|g|a (7) может быть нарушено в области частот оо^4п‘1Оэ рад-с"1. При этом вблизи максимума F-слоя в некоторой области углов а возникает область прозрачности для волн обыкновенной поляризации. Так, при a=85°r w=4n*103 рад-с"1 получим из (1): п3^-1,56•1 О5. Из рис. 2 видно, что в этом же направлении может распространяться и необыкновенная волна na = 2,3-10**.
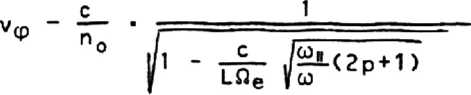
Диапазон R В этом диапазоне роль гирации уменьшается (д~(о) , и при о>«П2 возникает низкочастотная мода, характеризуемая изотропным Сне зависящим от угла а) распределением показателя преломления па=е1. (13) Такой показатель преломления, характерный для альфвеновских волн йе п2 = — , (14) Па Р возникает п из (11) в пределе низких частот Фа«Па . В области слоя F ионный состав плазмы меняется слабо, так что профиль волновода определяется, в основном, профилем ионизации слоя. Такой профиль показателя преломления вблизи максимума (2=2о)может быть аппроксимирован параболическим распределением (рис. 3) П - I о 2аа где масштаб оценивается величиной 3^80-120 км, по - максимальное значение показателя преломления. Такое приближение удобно как для высокочастотного (cdh> ti>QH), так и для низкочастотного (со<Пн) диапазона. Волноводная полость в верхней ионосфере Наряду с двумя отмеченными волноводами, расположенными вблизи максимума F-слоя, следует отметить еще один волновод, близкий по свойствам к (11), но расположенный выше F-слоя. Такой волновод захватывает излучение в частотном диапазоне (11)-(12). Высотный профиль показателя преломления п таких волн во внешней ионосфере определяется двумя противоположными тенденциями: уменьшением п с высотой Z из-за ослабления геомагнитного поля Н~ (Ro + Z)~3, где Ro - радиус Земли, и ростом из-за увеличения с высотой доли легких ионов Н + и Не++ (рис. 4). Оба этих эффекта вносят вклад в изменение частоты Пр (12). Конкуренция этих тенденций может привести к образованию на высотах Z = (1Z5-2Z5)•1 О3 км области максиму- Рис. 3. Высотный профиль показателя преломления необыкновенной волны в слое F при квазипродольном распространении (со—3 • 1 0 ^ рад* с" ) Рис. 4. Ионный состав многокомпонентной плазмы верхней ионосферы: кривые 1, 2, 3 относятся к ионам Н+, 0+, Не+ ма п, то есть к формированию во внешней ионосфере волновода для альфвеновских волн. В отличие от локализации альфвеновских волн вблизи максимума слоя F на высотах 300—500 км указанная область формируется на участке монотонного распределения электронной плотности, ионного состава и магнитного поля за счет разницы в характерных масштабах этих распределений. Обсуждаемый механизм локализации волн в многокомпонентной ионосферной плазме, обусловленный неоднородностью хи-' мического состава ионосферы, позволяет говорить о своеобразном волноводе для низкочастотных волн. Высотный профиль показателя преломления альфвеновских волн необыкновенной поляризации можно представить в виде О2. • Юэ n2(Z) = ---------F(Z)z (16) со2 . 1,84 но * где Оео и (он^ - лэнгмюровская и гирочастота электрона на некоторой высоте Zo; безразмерная функция F(Z) равна F(Z> " ' в^та ; ny(z) ®у(^ = Ne(Z) ' Ro+Z \б Му «7^7/ ; BY = М~ ' параметр L связан с неоднородностью геомагнитного поля в дипольной модели; Ме и Ny - плотности электронов и ионов сорта у на высоте Z; М и Му - массы протона и иона сорта у. Для построения функции F(Z) можно использовать модель высотного распределения концентрации ионов с учетом температуры [5]. Высотный ход n2(Z), построенный с учетом [5], обнаруживает максимум на высоте Zm=2z4-103 км (рис. 5). Этот максимум и соответствует волноводу для альфвеновских волн необыкновенной поляризации. Следует отметить, в отличие от слоя F, существенную асимметрию указанного волновода. Р и.с . 5* Высотный профиль показателя преломления (16) для частоты со=2п-10э рад*с-1 Сравнение обсуждаемого волновода с другим асимметричным волноводным каналом, возникающим для альфвеновских волн на границе плазмопаузы [6], позволяет отметить разницу в спектральных диапазонах захваченных волн; так как высота этого волноводного слоя z0~3RQ (Ro - pa диус Земли), а ионный состав плазмы определяется протонами, то вблизи плоскости экватора Qh~35 рад-с”1 и частоты км захваченных волн, ограниченные условием 0) Характерная длина затухания волн Lx определяется декрементом затухания х LX = ~ , <18) * сох где величина х находится из общей формулы (1). В обсуждаемом диапазоне частот вклад ион-молекулярных столкновений в затуха' ние, определяемое ^^ и Imgz часто превышает вклад электронных столкновений. Так, в низких широтах в ночных условиях вблизи максимума F-слоя v-jm-O,! с” ; при этом для волны частоты f = 15 Гц показатель преломления и длина затухания Lx составляет п=1,7*103 и Lx = (1,5-2)•1 О3 км; для частоты f = 10 Гц эти величины составляют п=0,9*103 и Lx=4-103 км соответственно. При переходе к более высоким частотам длина затухания возрастает. Так, для й)«10й рад-с-1 при квазипродольном распространении в ночных условиях длина Lx составляет Lx-10ц км. Спектральные свойства ионосферных плазменных волноводов, рассмотренные в этом разделе, будут применены нами для анализа фазовых эффектов в таких волноводах . Фазовые эффекты в многомодовых полях ионосферных волноводов Фазовые эффекты в полях, распространяющихся в ионосферной плазме, представляют интерес как для диагностики параметров плазмы, так и для локализации источников излучения. В модели одномодового поля в неограниченной плазменной среде плотность электронов можно выразить через отношение компонент электрического и магнитного полей волны; направление волнового вектора находится, с точностью до знака, по фазовым сдвигам между компонентами магнитного поля волны [4]. В отличие от этого, при волноводном режиме в неоднородной плазме диагностические воз-ложности могут быть связаны с дисперсионными характеристиками волноводных мод. Для построения таких характеристик целесообразно использовать уравнения Максвел* ла для электрических Е и магнитных Н компонент волнового поля в сферической сис-теме координат (р, 6# ф) в виде (0=90° на экваторе): i 3 ЕФ 1 9Ео R Эв tge sine Эф ' с(19) 1 аЕ« ЗЕф Rsi пб Эф 9R R- ’ ~Н6;(20) 9Ее Ее 1 3Er1ш 9R + R R Эб“ ■ с-НФ;(21) где p=r0+z; Ro - радиус Земли; Z - высота точки наблюдения, можно записать уравнения Максвелла для интересующих нас волн при условиях: (Кер)»1; <Кфр)»1 1Кббф-1Кфвд — с Пр, 0 - угол между геомагнитным полем HQ и волновым вектором К, лежащим в плос кости магнитного меридиана; величины Е , Е и Е связаны с компонентами тензора диэлектрической прони-123 цаемости плазмы е ц и е^: е1 = Eysin2 Р + Ej^cosap; Еа = ецсоза 3 + ExsinaB;(32) £3 = siп0-со53(ец-£1). Угол 3 определяется через магнитную широту 6т известной формулой [?] cos em cos 0 = - -- ■■-.. —- •(33) V i+3 sin2 em На экваторе 6=90°, a=0. Целесообразно рассмотреть в рамках системы (26)-(31) модели меридионального и широтного распространения волн по отдельности. При преобразовании обсуждаемой системы оказываются полезны тождества, следующие из (32): е1е2 * Е3 = СП6^ Е1 sin £ + £3 cos 0 = Eysin В; ( 54) g—0) Простейший случай связан с распространением низкочастотных (со2<<02, волн необыкновенной поляризации в плоскости меридиана (Кф=0, Кд^О). В этом слу чае, подставляя hp из (26) и hg из (27) и (31), получим волновое уравнение от носительно компоненты еф: Эавф 3Z2 cd2 <—Е1 - ке)еФ = 0 С Волноводный эффект проявляется здесь в существовании, наряду с поперечными компонентами поля h_ и вф, i с 3 1ф he = ~ “ • продольной компоненты магнитного поля hgI|KQ: В рассматриваемом низкочастотном пределе волноводная полость изотропна. В противоположном случае (о)2»Пн) показатель преломления слабо зависит от угла а лишь в конечной области углов а вокруг магнитного поля (см. рис. 1). В этом случае, соответствующем квазипродольному распространению (Кф~0) в низких широтах, уравнения, описывающие волноводный режим, получаются из системы (26)-(31) следующей процедурой: а ) из (29) и (30) выразим 1р и 1g: , ice ЗЬФ е сК lP = ^(1ge« cos3el ice ЭКф е3сК le = ~(ige" ”пр1ч> " ЧГ” ~ + ”b~h«’)' б ) составим входящую в уравнение (31) комбинацию lg sin з - LpCOsP = —(iglq + ~sinP j^ + ^cos^Kq) . Тогда (31) примет вид: dbg . . . 3 h।(p -— - iKhn = - —Ге iU + -^(i glm ♦ -—si n@ -r— + — cos0) ’(40) Эр Pc 1 1 Ф C| V co Эр ыФ Для упрощения дальнейших преобразований рассмотрим предел 3—0; подставляя Lp и Lg (37)-(38) в (28), получим: — • --— + (—Е - К ) Ьф = —д1ф.(41) е« Эр2 с2с Опуская здесь слагаемое с малым параметром ( I е^ ejp1 | <:10-6) z выразим из (41) Ьф через 1ф и подставим в (40). Подставляя туда же выражения для hp и hg из (26) и (27), получим волновое уравнение для компоненты 1ф Э 2 — ♦ рМ61 ♦ а) - К^] 1ф = 0. Эр с Профиль волноводной полости в р-слое, определяемый профилем ионизации, удобно аппроксимировать параболой (15). При этом спектр поперечных волновых чисел К2 в р-й моде определяется формулой: й>по Kip ” ти^<2р + 1)- <43) Соответственно, длина волны Хр в р-й моде определяется формулами Фазовая скорость в этой же моде составляет Выражение под корнем в (45), учитывающее поправку на волноводный режим, мало отличается от единицы: так, при ojz10u рад*с~1, L~1 О2 км, Пе-З’^О7 рад*с-1 (ночные условия) вычитаемая величина под корнем составляет 2 • 10”3 (2р + 1) . Поэто му Уф можно представить в виде, удобном для оценок модовых эффектов: При этом разность фазовых скоростей в двух соседних модах составляет Существенно, что в рассматриваемой модели разность фазовых скоростей на за висит от несущей частоты. Рассмотрим теперь на основе полученных формул некоторые фазовые эффекты в ионосферном волноводе. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ПЛОТНОСТИ ЭЛЕКТРОНОВ В МАКСИМУМЕ СЛОЯ F Такое определение можно вести, измеряя "фазовое*1 время распространения t сигнала между двумя КА в волноводе. Предположим, что длина лучевой траектории между КА равна lz а время распространения первой из принятых мод составляет t. Зная эти величины, можно определить среднее значение показателя преломления п0 на трассе и найти отсюда среднюю на трассе плотность электронов в максимуме слоя : ^ ср moxnH 4тге2 Производя одновременные измерения на нескольких частотах о), можно уточнить значение Ncp . ДИСТАНЦИОННОЕ ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОЙ ТОЛЩИНЫ СЛОЯ F Эту величину (параметр L в (47)) можно оценить, измеряя разность времен распространения двух мод At, излученных одним КА и принятых другим КА. Как легко видеть, At связана с разностью Ауф (47): l-AV(p (49) ------- = At . Комбинируя (49) с (48), можно исключить длину трассы L: = м V D I At со — . 1 п • Дер Подставляя сюда величину П^ , связанную со средней плотностью электронов ^ср (48), можно вычислить параметр слоя L. При этом запаздывание At связано с Фазовым сдвигом известным соотношением: At = ^ • <5,) СО Таким образом, за один виток КА может быть построен профиль L в некоторой полосе вдоль кругосветной траектории КА. Такой результат, важный для планетарной динамики F-слоя, невозможно получить зондированием от стационарного наземного источника. Существенно, что измерения At удобно вести именно фазовыми методами из-за малых значений этой величины. Так, при со—3 • 10 ** рад-с-1 (vx5 кГц) в ночных условиях по=90, Уф=3,3-103 км*с-1 и Дуф=3,8 км-с"1. В этом случае задержка At при расстоянии 1=800 км составляет At=0,28 мс, что соответствует 1,4 периода колебаний волнового поля с длиной волны Л=2тсс (соп0)~12б50 м. Фазовый сдвиг между моментами регистрации прихода обеих мод составляет здесь Дф=2,8п. При уменьшении частоты волны в m раз временное запаздывание возрастет во столько же раз, но фазовый сдвиг Дф в модели (42) не изменится. Описанный здесь фазовый метод позволяет использовать специфику волноводных режимов распространения низкочастотных волн для определения параметров глобальных неоднородностей космической плазмы. В отличие от этого, ниже показано два метода определения взаимного положения КА, также основанных на фазовых эффектах. ЛОКАЦИЯ ИЗЛУЧАТЕЛЯ В ВОЛНОВОДЕ ПО ЗАПАЗДЫВАНИЮ МОД Расстояние- I между двумя сечениями волновода, проходящими через мгновенные положения КА перпендикулярно волновой нормали, можно оценить из (49)z подставляя туда запаздывание At, выраженное через фазовый сдвиг Дф I = -2L • ^2 . (52) Дуф ед Выражение (52) справедливо при любой модели показателя преломления по. В частности, в обсуждаемом здесь случае п2 = й2(ахон)"1 получим, подставляя в (52) значения v2 и АУф из (46)-(47)z особенно простую формулу: I = 1*Дф. (53) Интересно отметить, что найденная величина фазового сдвига Дф не зависит от моды распространения. Поэтому по сохранению сдвига можно судить о применимости обсуждаемой модели для описания ионосферного волновода. Характерной особенностью такой локализации является использование высоких мод (р»1). Высота 2р,ограничивающая область локализации р-й моды, определяется формулой 7 - ./с L ( 2 р УГГ р wno Как видно, при ш-З-ТО* рад-с-1, nQ = 90 и р=0 (основная мода) область ZQ вокруг максимума слоя невелика: Zо=3 км; при р=15 величина ZQ возрастает до 18 км. При уменьшении частоты cd величина Zp медленно растет Zp-co-1/1*. Оценка направления движения источника Сближение или взаимное удаление двух КА можно оценить с помощью эффекта Допплера. Из-за большого значения показателя преломления nQ частота сигнала, принятого на спутнике, оказывается сдвинутой по отношению к частоте, излученной другим КА, на величину Ди): — = —- • cosa, (55) где a - угол между волновыми векторами излучения и вектором относительной ско-рости движения тел vq . Так, при сближении спутников со скоростью vo=16 км'С-1 величина Део составляет Дсо=3*10~2 cos со. При cos a-1 (a—0) и со«3‘10* рад«с~1 Асо составляет величину Дсод150 рад«с . По мере сближения КА (cos а уменьшается) сдвиг частоты умень- шается , переходя через 0 в момент минимального расстояния между КА, после чего сдвиг частоты меняет знак [8,9]. При допплеровских измерениях регистрация дрейфа частоты позволяет оценить направление движения КА по его радиоизлучению. При регистрации импульсов полезно знать характерную длину дисперсионного расплывания импульса Ьш: Lto ” dco Э v VrP dK ' v“ W где vrp - групповая скорость сигнала; То - его характерная длительность. Для модели п’»Д^(ахон) легко найти групповую скорость в виде В этой формуле вычитаемые в числителе и знаменателе составляют малые величины порядка 10“2-10_3, так что основной вклад в дисперсию вносят плазменные эффекты с vzx = ----- . <*> con При этом 8сот; Оценка для импульса, содержащего 50 колебаний поля с частотой цу=3'Ю4 рад-с“\ приводит к большей величине Ltlj“2,104 км, что с большим запасом (на порядок) превышает характерные длины, ограничивающие область применения обсуждаемого здесь квазипродольного распространения для низких широт. При понижении частоты to дисперсионная длина Ьш падает так, что для о>=3 * 103 рад-с-1 длина 1Ш для импульса, содержащего 50 колебаний, составляет всего Lo>=600 км. Таким образом, в низкочастотной части спектра волн, захваченных в волновод дисперсионное расплывание импульса на расстояниях LZ103 км может быть существенным. Таким образом, методы фазовой диагностики изотропной плазмы основаны на использовании интерференции плоских волн, поле которых не имеет модовой структуры. В отличие от этого фазовые эффекты в волноводе открывают принципиально новые возможности диагностики, связанные с модовой структурой поля и разностью фазовых скоростей мод. Такие эффекты играют важную роль при больших длинах распространения, соответствующих волноводам в космической плазме. Своеобразие таких эффектов исследовано в этой статье на примере дисперсионных свойств низкочастотных волноводных полостей, образуемых вблизи максимума F-слоя при регулярном ходе ионосферных параметров: 1. Высокие значения показателя преломления (п=102-103)z соответствуют километровому диапазону длин волн при низких частотах "и=0,5_5 кГц. 2. Низкое затухание обеспечивает большие длины распространения Lx = (5-8) • 103 км. 3. Волноводные режимы реализуются лишь для волн необыкновенной поляризации. Принципиальной особенностью волноводного режима является многомодовая структура волнового поля. Такая структура указывает на новые перспективы диагностики, основанные на определении фазового сдвига между модами: 1. Определение плотности электронов и эффективной толщины волновода, средних вдоль траектории волновой нормали. 2. Локация излучателя в волноводном слое. 2. Гинзбург В.Л. Распространение электромагнитных волн в плазме. М., Наука, 1967 . 3. Б о р и с о в Н.Д. Радиофизика Н Изв. вузов, XXVI, 2, 142 (1983). 4. R. L. 0. Storey and L е f е u г е. Journ. Royal Astrou. Soc. 56, 255 (1979). 5. И в а н о в - Холодный Г.С., Калинин Ю.К. Геомагнетизм и аэрономия, XXV, 3, 400 (1985). 6. Гульельми А.В. МГД-волны в околоземной плазме. М.: Наука, 1979- 7. Cereisier Y.C. Journ. Atm. Terr. Phys. 36, 1443 (1974) . 8. Багбая И.Д.,Водяницкий С.Я.,Шапин-с к и й В.В., Шварцбург А.Б. Ионосферный волновод для низкочастотных волн Н Техника средств связи, М., Экое, 3, (1988). 9. Б а г б а я И.Д., Водя ниц кий С.Я.,Шапин-с к и й В.В., Шварцбург А.Б. Компенсация искажений формы электромагнитных сигналов // Техника средств связи. М., Экое, 11 ( 1988) .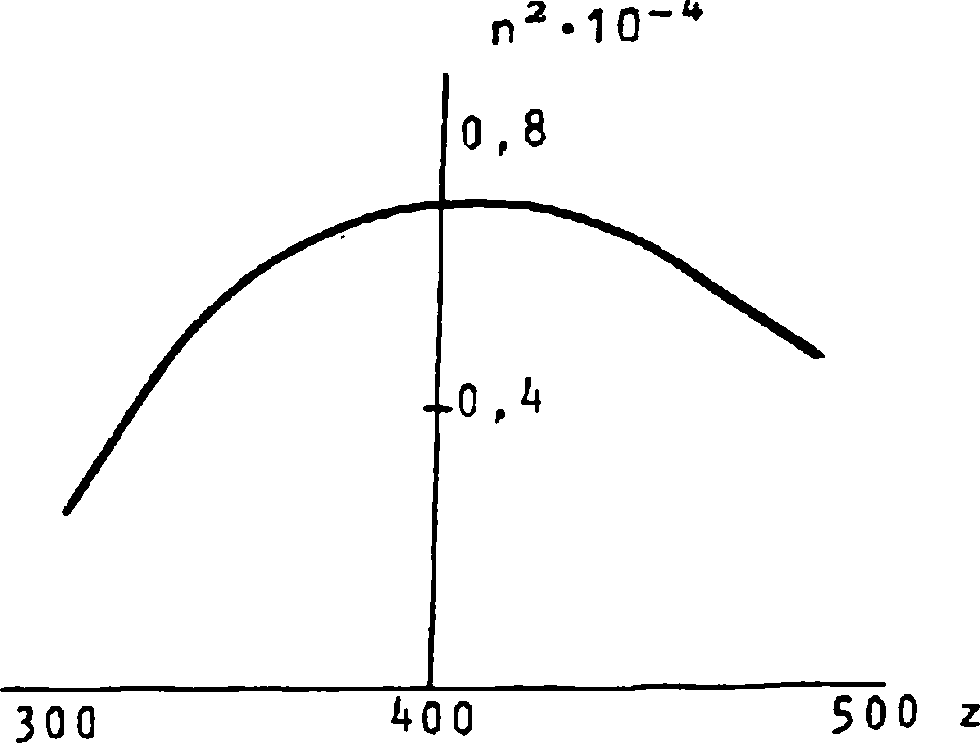
H, составляют величины 1-3 Гц.
э еф
iK(pep Эр
i CD
—he;
(27)
Эее
а?" " 1КееР "
icb h с Ф
(28)
iKQh(p - iKcph6
• - ^«p
+ fi3eQ + ig cos £eq];
(29)
3 Ьф
1KQhP " э^-
- ^[^з'р +
E3eg - ig sin 0еф];'
(30)
dhg
э^- " iK0hP =
- ^[Е1«ф+
ig(e@ sin 3 - ep cos 0)],
(31)
где