Фазовые переходы кубических нанокристаллов UO2

Диоксид урана является наиболее распространенным топливом в современных ядерных реакторах. Из таблеток диоксида урана формируются топливные сердечники тепловыделяющих элементов (твэл) [1]. Во время эксплуатации таблетки подвергаются воздействию высоких температур и давления, облучению, механическим нагрузкам. При номинальной мощности реактора температура на оси твэла может превышать 2000 К, а давление газообразных продуктов деления урана внутри герметичного твэла может достигать 80-100 атм [2].

Экспериментально процессы, происходящие в топливе при температурах близких к критическим, слабо изучены, поэтому моделирование служит хорошим источником для получения новой информации.

В данной работе с помощью молекулярнодинамического моделирования исследуются фазовые переходы наноразмерных кристаллов диоксида урана.

1. МЕТОД РАСЧЕТА

Моделирование проводилось с использованием программного комплекса DL_POLY [3]. В качестве модели был выбран кубический кристалл со свободными границами (нулевые граничные условия) Транслируемая ячейка была выбрана в виде кубического кристалла со структурой флюорита. Кристаллиты строились путем

трансляции элементарной ячейки по трем направлениям. В табл. 1 приведены размеры моделируемых кристаллитов и соответствующее число атомов в них.

Потенциал межатомного взаимодействия был выбран в форме Борна-Майера, что обеспечило минимальный набор параметров, некоторые из которых взяты в виде кусочно-линейных медленноменяющихся функций температуры:

+f(T)(b +bj)exp -

I

z(T)z (T)e ²

^j

ai +aj- rj b, +b, ij

-

cicj

6 , (1)

rij

где первое слагаемое соответствует кулоновскому взаимодействию, а второе и третье — потенциалу Борна-Майера [4]. Значения независимых от температуры параметров потенциала были взяты из работы [5]. Параметры z(Т) и f(T) задаются в виде кусочно-линейных функций:

<

z(T) = z o [ ^{1 + a} T ] , где « ={ f ( T ) = f 1 + P^ , где e=-

[ 9,6092 - 10 -3 , T <  T ⁰ , z„ = 1,192966, T = 2666 K

[ 29,27444 - 10 -3 , T >  T ₀

[ 9,34793 - 10 - ², T < T                 .        ()

<                ⁰, f =03540625, T ' = 2627 K

[ 2,59565 - 10 -1 , T >  T_o

Более подробно вопросы обоснования температурной зависимости указанных параметров потенциала рассмотрены в наших предыдущих работах [7, 8].

2. МЕТОДЫ ИДЕНТИФИКАЦИИ ТОЧКИ ПЛАВЛЕНИЯ

Для идентификации точки плавления в молекулярной динамике существует несколько методов. Наиболее распространенные следующие: анализ вида радиальной функции распределения

Таблица 1. Моделируемы кристаллы

Размер, эл яч еек	4x4x4	5x5x5	6x6x6	8x8x8	10x10x10
Размер, нм	2,2	2,7	3,3	4,4	5,5
Количе ст во атомо в	768	1500	2592	6114	12000

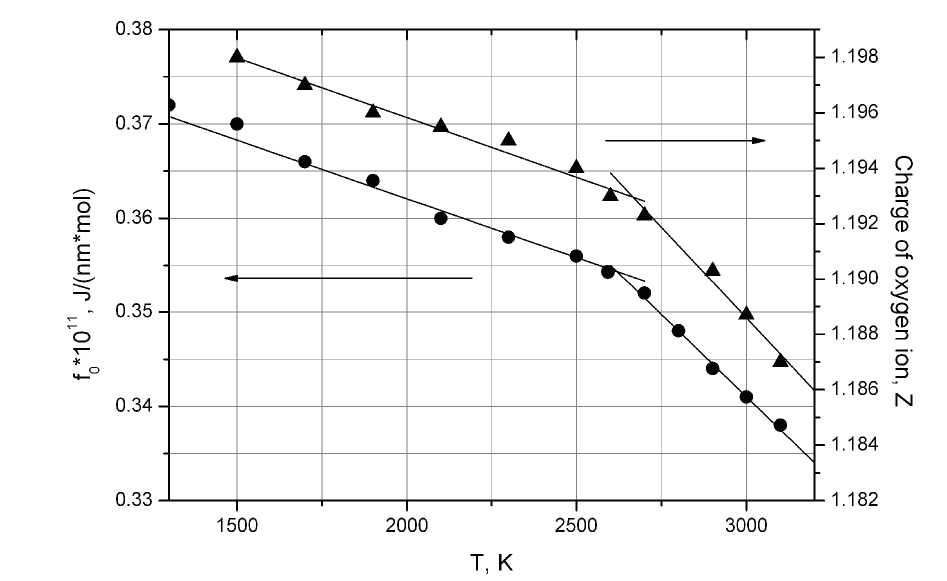
Рис. 1. Зависимость параметра f и дробного заряда иона кислорода от температуры и кусочно-линейная аппроксимация с переходом вблизи точки 2670 K [6]

(РФР), метод структурного фактора; анализ изменения энтальпии (метод калориметрической кривой).

• 1)    РФР вычисляется по формуле [9]:

V N ( R , A R )

g N 4nR ²A R ’         (3)

где – N число частиц моделируемого кристалла N(R, AR ) - число частиц находящихся в сферическом слое шириной A R .

Вид РФР позволяет качественно оценить находится ли материал в расплавленном или кристаллическом состоянии. Для упорядоченного состояния кристалла РФР представляет собой последовательность резких четких пиков, положение которых соответствует закономерности расположения атомов. Следует отметить, что первый пик присутствует всегда, в любом фазовом состоянии, тогда как второй и последующие пики при высоких температурах становятся более пологими и полностью исчезают, когда кристалл переходит в расплавленное состояние.

• 2)    Метод структурного фактора основан на анализе динамики изменения величины

^

S « (M

, которая вычисляется как нормирован-

ный квадрат модуля структурного фактора отдельно для подрешеток урана и кислорода в направлениях (001), (010) и (100) в соответствии с формулой [10]:

^

S « (к)

Ν ²

f ' N      ^ ^ ) ²

2 ^cos(k • r n )

V n =1                 7

+

+

f N           >   >  ^ ²

2 sin(k • rn)

V n = 1                  7

где индекс б – соответствует атомам урана или кислорода, N – количество атомов в системе, вектор k – вектор обратной решетки, r_n – радиус-вектор атома системы.

При 0 K кристалл представляет собой идеальную структуру, структурный фактор которой равен единице. Напротив, при высоких температурах для расплавленного состояния квадрат

модуля структурного фактора стремиться к нулю, а его численные оценки колеблются в диапазоне 0,01-0,04.

• 3)    В методе энтальпии фазовый переход идентифицируется по резкому скачку на температурной зависимости H(T). В нашей предыдущей работе [11], посвященной моделированию плавления диоксида урана эти методы рассмотрены более подробно.

• 3. ОПИСАНИЕ РЕЗУЛЬТАТОВ

Для ионного кристалла диоксида урана характерно наличие суперионного перехода. Поскольку масса иона урана многократно превосходит массу иона кислорода, то кислород в решетке более подвижен. То есть подрешетка кислорода оказывает менее стабильной и для перевода её в расплавное состояние требуется меньше энергии. Явление расплавления анионный подрешетке на фоне относительно упорядоченной катионный подрешетки и называется суперионным переходом. Этот эффект был впервые обнаружен экспериментально Бредингом [12] позже подтвержден в других работах.

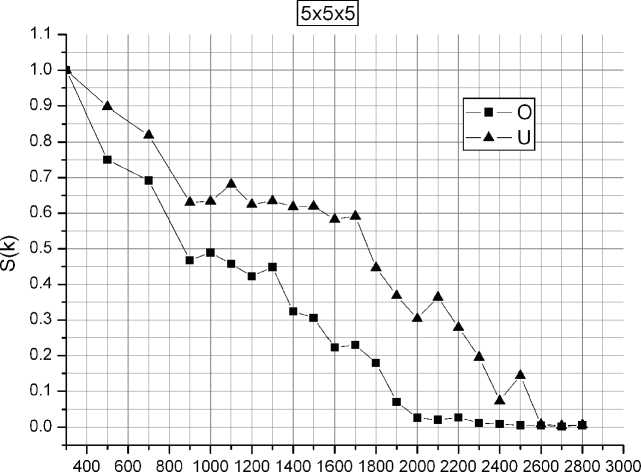
При исследовании фазовых переходов проводилось ступенчатое нагревание кристаллитов с шагом 100 К. На рис. 2 представлена зависимость структурного фактора от температуры для нанокристалла 5x5x5. При температуре 2000 К значение S(k) для кислородной подрешетки падает до значения порядка 0,03 относительных единиц. Это означает, что решетка расплавилась (суперионный переход). Для урановой подрешетки же S(k)

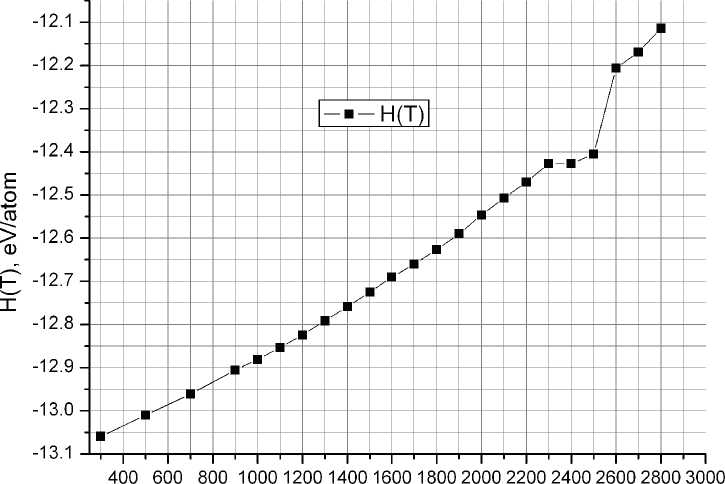
опускается до таких значений при температуре 2600 К, что соответствует плавлению. Об это свидетельствует и резкий скачок энтальпии (рис. 3), наблюдающийся при той же температуре.

Необходимо отметить, что при температуре 2100 К происходит трансформация нанокристалла: кубический кристалл, ограниченный плоскостями типа (100), принимает форму октаэдра (рис. 4). С этим связан скачок структурного фактора для ионов урана при данной температуре (рис. 2). Поверхность кристалла ограничена уже 4-мя плоскостями типа (111) и двумя типа (100). Вероятно, что при более длительной релаксации кристалл примет форму правильного октаэдра. Этот эффект также был зафиксирован в работе [13], где авторы, проводя МД моделирование нанокристалла, наблюдали подобную трансформацию для кристалла 8х8х8 при температуре 2200 К.

Применяя аналогичную методику и рассуждения были, найдены температуры фазовых переходов для кристаллов других размеров. Результаты приведены в табл. 2. Также для сравнения в таблице указаны результаты МД расчета, полученные в работе [14].

Поскольку шаг по температуре на всех зависимостях составлял 100 К, то в качестве оценки абсолютной погрешности было выбрано значение ±50 К. Приведенные экспериментальные значения критических температур относятся к макрокристаллам, а для нанокристаллов в литературе данных нет. Однако следует ожидать эффект снижения температуры плавления при переходе к наноразмерным системам.

Temperature, К

Рис. 2. Зависимость структурного фактора от температуры для кислородной и урановой подрешетки нанокристалла UO₂

Temperature, К

Рис. 3. Зависимость энтальпии от температуры для нанокристалла 5x5x5

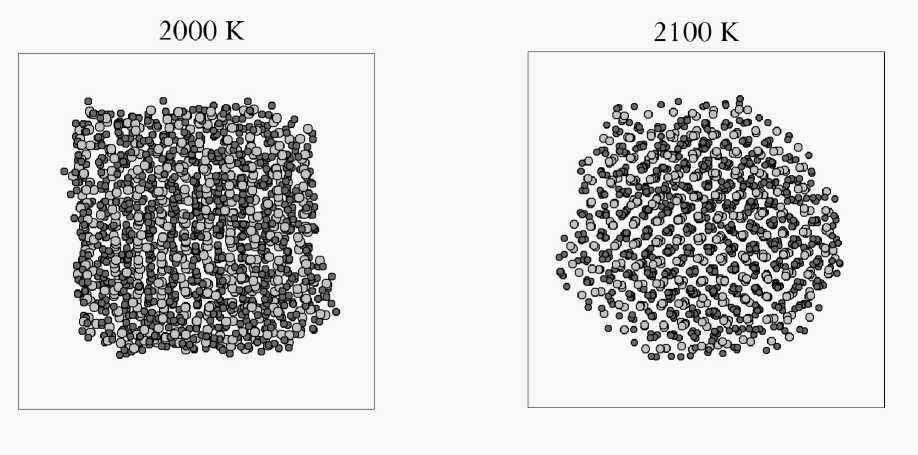
Рис. 4. Изменение формы нанокристалла от кубической к октаэдральной

Таблица 2. Температуры фазовых переходов для кубических нанокристаллов

Размер, нм ( число ионов)	Суперионный п ере ход T λ , К	Плавление Т m , K
		Данная работа	Результ аты рабо ты [13]
2,2 (786)	1800	2300	2040
2,7 (1500)	2000	2600	2385
3,3 (2592)	2400	2700	2680
4,4 (6144)	2500	2800	2955
5,5 (12000)	2600	2800	3050
Эксп ерим ен ты	2670 [6]	3150 ± 20, 3138 ± 15, 3113		± 20 [6]

ЗАКЛЮЧЕНИЕ

С помощью метода молекулярной динамики были рассчитаны температуры фазовых переходов нанокристаллов в диапазоне размеров 2,2 – 5,5 нм. С уменьшение размера происходит снижение температур суперионного перехода и плавления. Установлено, что вблизи точки плавления происходит трансформация нанокристаллов: кубический кристалл принимает форму октаэдра.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг., федеральной целевой программы « Научные и научно-педагогические кадры инновационной России на 2009-2013 годы » и « Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2012 годы » , а также при частичной поддержке гранта РФФИ: проект № « 12-08-97076-р_поволжье_а » .