Фазовые переходы в твёрдых электролитах на основе Na-(β-β '')-глинозёма
Автор: Пушкин А.А., Маловицкий Ю.Н., Римкевич В.С., Барышников С.В.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Физика и электроника
Статья в выпуске: 4-1 т.12, 2010 года.
Бесплатный доступ
Экспериментально обнаружен скачок электронной проводимости на её температурной зависимости в области низких температур в Na-(?-?'')-глинозёме как чистом, так и легированном иттрием, медью, висмутом или свинцом. Отмечено, что этот эффект наблюдается в той же температурной области, что и суперионный переход, наблюдавшийся ранее другими авторами в Na-?-глинозёме. Обнаруженный нами скачок электронной проводимости проанализирован нами в рамках вибронной концепции.
Скачок электронной проводимости, фазовый переход, вибронная концепция
Короткий адрес: https://sciup.org/148199389
IDR: 148199389 | УДК: 538.935
Текст научной статьи Фазовые переходы в твёрдых электролитах на основе Na-(β-β '')-глинозёма
В работе [1] приведён график температурной зависимости проводимости, на котором наблюдается скачок проводимости на два порядка в области низких температур. Фазовый переход объяснён в модели кулоновского взаимодействия дефектов. В данной работе мы объясняем этот фазовый переход при помощи вибронной теории.
В работе для решения вопроса о суперионных переходах проводились измерения электронной проводимости на постоянном токе при низкой температуре (рис. 1). Измерения проводились на поликристаллических образцах полиалюминатов натрия с различным содержанием иттрия, меди, свинца или висмута (до 10ат.%), приготовленных по методике [2].
На всех образцах наблюдалось резкое увеличение проводимости при повышении температуры в области (240±20)К, т.е. наблюдался фазовый переход.
Общая теория, описывающая фазовые переходы в суперионное состояние в твёрдых электролитах развивается в работе [1].
Как следует из графика в работе [1], при температуре 130 - 200 К в Na-p-глинозёме наблюдается увеличение проводимости примерно в 200 раз. Это свидетельствует о наличии фазового перехода, который является сильным по терминологии [1]. Используя параметры перехода, а также уравнения развитой авторами [1] для твёрдых электролитов теории, составим следующую систему уравнений [3], описывающую фазовый переход в Na-p-глинозёме ln О"3 - ln <71 = ((wx 1 - Ax /2) -
- ( wx 3 - A x 32 /2))/ kT , = 5,3
< x 1 = V exp( - w /2 kT r )
x 3 = 1 -v • exp( - ( w - A )/kT r ) • (1)
A = (2 w - 2 kTfr ) - 2 kT r ln v
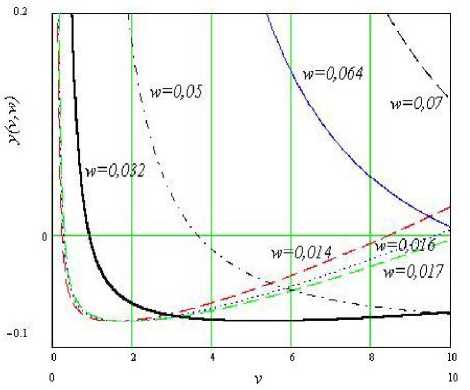
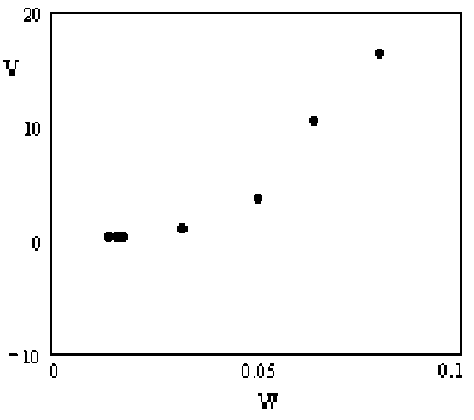
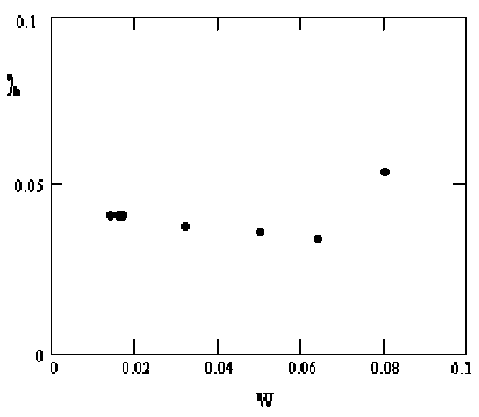
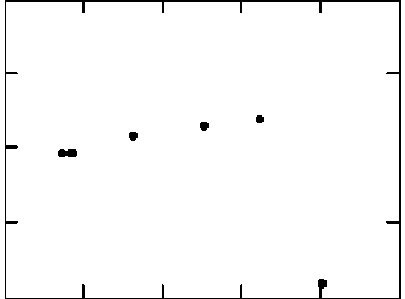
Получаем систему четырёх уравнений с пятью неизвестными: w, x1, x3, X, v, которые представляют собой, соответственно, энергию образования дефектов, относительные концентрации дефектов ниже и выше перехода по температуре, константу, характеризующую кулоновское взаимодействие дефектов и параметр, характеризующий изменение частоты колебаний иона при его выходе в междоузлие. Число 5,3 в правой части первого уравнения (1) – величина скачка проводимости в масштабе рисунка. Вообще говоря, система 4 уравнений с 5 неизвестными не имеет однозначного решения, и поэтому она требует тщательного исследования областей допустимых значений параметров. Во-первых, очевидно, что относительные концентрации де- фектов х1 и х3 должны принимать значения от 0 до 1. Далее, эффективное кулоновское притяжение, необходимое для осуществления перехода, может возникнуть только при λ>0. Второе – четвёртое уравнения получены в приближении 1<ν<10. Энергия образования дефекта w снизу ограничена уровнем тепловых колебаний kTtr=0,014эВ, а сверху величиной энергии образования дефекта для обычных кристаллов. Следовательно, энергия образования дефекта принимает значения 0,014 Из системы уравнений (1) получаем следующее уравнение относительно параметров w и ν: w( ν⋅exp(-0,0w28)-1+ 0,ν135⋅exp(0,0w14))+(w-0,014(1+lnν))× w 0,027 w 0,018 w (2) ×(1-ν⋅exp(-0,014)- ν ⋅exp(0,014)+ ν2 ⋅exp(0,007))-0,074=0 Обозначим правую часть уравнения (3) через y. Получим уравнение y=f(w, v), которое представляет собой поверхность в координатах (w, ν, y). Решения уравнения (3) представляют собой кривые, которые получаются при пересечении поверхностей y=f(w, v) с плоскостью y=0. Для решения этого уравнения будем использовать компьютерную программу Mathcad 2000. Для того, чтобы сузить область допустимых значений w, будем рассекать эту поверхность плоскостями w=const. Сечения поверхности плоскостями представляют собой кривые второго порядка в координатах (ν, y). Такие кривые изображены на рис. 2. Решениями системы являются точки их пересечения с прямой y=0. Из рис. 2 видно, что математические решения уравнения (3) существуют в диапазонах 0,014 Решения уравнения (3), соответствующие сечениям, показанным на рис. 2, т.е. значения параметра ν, соответствующие выбранным w, приведены на рис. 3. Из этого рисунка видно, что значения параметра н попадают в область его допустимых значений только при малых w. Для проверки области существования эффективного кулоновского притяжения между дефектами рассчитываем значения λ. Положительные значения л, как видно из рис. 4, получаются для всех значений w в указанных диапазонах: 0,014 Теоретически нами показано, что в модели кулоновского взаимодействия между дефектами фазовые переходы описать нельзя. Следовательно, они возникают по другой причине. На рис. 1 приведены экспериментальные зависимости проводимости от температуры при низких температурах. На всех образцах наблюдаются скачки проводимости при температуре (240±20)К, которые свидетельствуют о наличии фазовых переходов в данных материалах. Мы предлагаем попытку описания фазовых переходов при помощи вибронной теории. Обратим внимание, что кривые на рис. 1 разбиваются на две группы, которые можно условно представить как d-элементы (образцы, легированные иттрием и ме- Рис. 1. Зависимость сопротивления от температуры для образцов Na-b-глинозёма, легированном иттрием, висмутом, медью, свинцом и чистого Рис. 2. Сечения поверхности y=f(w, ν) поверхностями w=const Рис. 3. Решения уравнения y(ν, w)=0 при выбранных на рис. 2 значениях w=const Рис. 4. Значения эффективного параметра λ для выбранных на рис. 2 значений w=const К 5 -10 "20 -30___________________________________________ О 0.02 0.04 0.06 0.08 0.1 W Рис. 5. Значения параметра х3 для выбранных на рис. 2 значений параметра w=const. дью) и р-элементы (Na-β-глинозём, чистый и легированный висмутом и свинцом). Кривые, относящиеся к группе d-элементов, имеют переход при температуре 230К, что соответствует 175 см-1. Так, например, в случае Na(Y)-(β-β'')-глинозёма эта величина хорошо согласуется с переходом между двумя t2g – подуровнями иттрия – верхним и нижним (98 +77) см-1 [4]. Тогда получается, что этот переход может быть описан по (Т – t2) задаче эффекта Яна – Теллера для октаэдрического фрагмента элементарной ячейки с ионом иттрия в центре. Неустойчивость системы при легировании иттрием проверяется, исходя из оценочных значений силовых констант FT и KT. Силовая константа КТ рассчитывается, исходя из частоты колебаний иона иттрия по ИК – спектру, а вибронная константа FT, исходя из значений силовой константы [5]. При расчёте данные ИК-спектра возьмём из [6] и положим смещение иона кислорода равным 1А. Тогда величи- на (FT)2/(KT)≈0,035 эВ, что существенно больше, чем расстояние между подуровнями 100 см-1≈ 0,012 эВ. Таким образом, неустойчивость системы Na(Y)-(β-β'')-глинозёма показана. Обратимся к Na-(β-β'')-глинозёму, легированному медью. Поскольку известно, что для меди активным является электронный Е-терм, то переход в системе, элементарная ячейка которой содержит октаэдр с медью в качестве центрального иона должен описываться по (Е – е) – задаче эффекта Яна – Теллера. Различие температур перехода в системах, содержащих октаэдры с иттрием и медью в качестве центральных ионов, считаем связанной с различной величиной расщепления вырожденных уровней t2g-иттрия и eg-меди. К сожалению, не удалось рассчитать виб-ронные константы и применить критерий устойчивости к Na-(β-β'')-глинозёму, легированному другими элементами. Однако, считаем необходимым высказать свои соображения относительно Na-(β-β'')-глинозёмов, чистого и легированного висмутом и свинцом. Системы, включающие октаэдры с р-элементами в качестве центрального иона, испытывают фазовый переход при температуре 250 К, что соответствует 185 см-1 и, по-видимому, этот переход может быть описан в соответствии с (s+p – t1u) задачей псевдоэффекта Яна - Теллера. Смещение температуры фазового перехода мы считаем связанным с различным расстоянием между псевдовырожденными уровнями. Таким образом, в работе обнаружен отклик электронной подсистемы, выражающийся в скачке электронной проводимости, на фазовый переход в Na-β-глинозёме, как чистом, так и легированном медью, иттрием, свинцом и висмутом. Этот фазовый переход мы связываем с кооперативным эффектом Яна – Теллера в одних соеди- нениях и псевдоэффектом Яна – Теллера в других. Зависимость температуры фазового перехода от вида центрального иона октаэдрического фрагмента мы связываем с различной величиной расщепления вырожденных уровней в эффекте Яна – Теллера или расстояния между близкими подуровнями в псевдоэффекте Яна – Теллера. В заключение мы считаем своим приятным долгом поблагодарить А.В. Куликовского за полезное обсуждение и помощь в выборе метода решения системы уравнений, проф. В.Е. Карасёва, проф. Н.Г. Галкина, проф. Ю.Т. Левицкого за плодотворные дискуссии. Мы также признательны Р.А. Климанову, А.Н. Гончару и А.С. Истомину за помощь в подготовке образцов.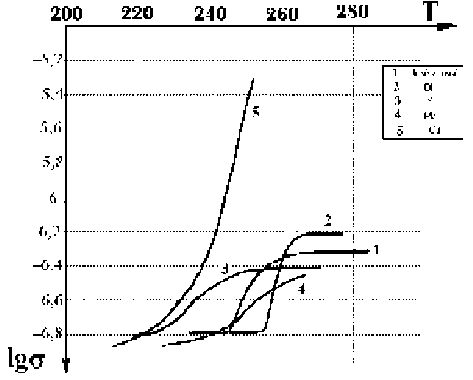
Список литературы Фазовые переходы в твёрдых электролитах на основе Na-(β-β '')-глинозёма
- Ю.Я. Гуревич, Ю.И. Харкац. Суперионные проводники. М.: Наука, 1992. 288 c.
- Ю.Т. Левицкий, Ю.Н. Маловицкий, А.А. Пушкин. Электронная электропроводность в системе Na2O.nAl2O3 -Y2O3//Неорганические материалы. 2003. №9. С. 971 -973.
- Пушкин А.А. Фазовые переходы в суперионное состояние в Na глинозёме//Дальневосточный вестник высшей школы. 2001. Вып.1. С. 52 -56.
- Ю.Н. Маловицкий, А.А. Пушкин, Ю.Т. Левицкий. Электронные процессы в газовых сенсорах на основе Na ('') глинозёмов//Вестник ДВО РАН. 2005. №6. С. 22-26.
- Б.И. Берсукер. Эффект Яна Теллера и вибронные взаимодействия в современной химии. М.: Наука, 1987. 344 с.
- Ю.Т. Левицкий, Ю. Н. Маловицкий, А.А. Пушкин. Исследование структуры Na(Y) и Na глинозёмов методом ИК спектроскопии//Перспективные материалы, 2003. №4. С. 93-95.


