Фазовые равновесия в системе Hg-Se при вакуумной дистилляции

Для разделения компонентов металлических сплавов используют вакуумную перегонку ‒ экологически безопасную и высокопроизводительную пирометаллургическую технологию, основанную на различии в давлении насыщенных паров чистых металлов ( Р^* ) при одинаковой температуре, характеризующихся коэффициентами разделения (β) при распределении металлов между газовой и жидкой фазами [1–4]. Состав продуктов воз-

гонки и степень разделения компонентов сплава при заданных значениях температуры и давления осуществляют при помощи рассчитанных равновесных фазовых диаграмм VLE ( vapor liquid equilibrium ), в частности, температура – состав « Т – х » и давление – состав « Р – х » [5–8]. Для определения β необходимо рассчитать коэффициенты активности компонентов (γ _i , γ j ), зависящие от температуры и состава cплава, с использованием объемной модели молекулярного взаимодействия

MIVM (molecular interaction volume model) . При расчете используют значения координационных чисел ( Z ), молярных объемов ( V_m ) и потенциальных энергий парного взаимодействия ( В ) компонентов сплава. Диаграммы VLE помогают выявить вероятностные диапазоны температуры и давления процесса дистилляции, соответствующие заданной степени разделения компонентов исходного сплава и составу образующихся конденсата и огарка. Поскольку процесс расчета MIVM является относительно сложным, особенно расчет первых координационных чисел Z i и молекулярного объема V mi компонентов сплавов, использовали метод прогнозирования, включающий меньшее число параметров системы, так называемый упрощенный MIVM или SMIVM (simple molecular interaction volume model) . Поэтому активность компонентов Hg–Se сплавов и фазовые диаграммы VLE были рассчитаны с использованием модели SMIVM . Оптимальные параметры процесса разделения компонентов сплавов можно оперативно получить из VLE фазовых диаграмм [9–12].

Теоретический анализ

Летучесть (фугитивность) каждого компонента в газовой и жидкой фазах равны, когда система достигает равновесия. Соотношение общего равновесия для VLE может быть выражено следующим образом:

ф(ViP) = фр1(XiY)exp|V (Ркрi )]. (1) где ф^ и ф^ - коэффициенты летучести (фугитивности) i-компонента в газовой фазе и при давлении насыщенного пара; xi и yi ‒ молярные доли жидкой и газовой фазы i-компонента; P и T ‒ общее давление и температура в равновесной системе; γi ‒ коэффициент активности в жидкой фазе; рfat- давление насыщенного пара чистого г-компонента при температуре T; Vi - молярный объем жидкости; R ‒ универсальная газовая постоянная.

При низком давлении ( Р ≤ 133 Па), используемом в данном исследовании, коэффициент

Г v^l( Р - р S ^at)l exp|    •-    |

Пойнтинга

• 1.    В добавлении, газовая фаза может рассматриваться как идеальный

газ и зависимостью фугитивности жидкой фазы от давления можно пренебречь. Уравнение (1)

может быть выражено следующим образом:

V i p = X i Y i p ,"¹ ( i = 1, 2, .... N) .

Если жидкая смесь идеальна, то по закону Рауля γ i = 1. Для бинарного сплава:

xi + xj = 1, yi + yj = 1, p = p?at yi^Xi + pfatYjXj = p-at yiXi + pjat yj (1 - Xi).

Из уравнений (2) и (4) можно выразить x i и у i как:

_  Р - P, “' y ,       _

^X i = _n sat_v. sat_v ,. ^y i = ^р [ Y i ^р , Y ,

P S ^atY i X i

Р .

Модель MIVM считается одной из наиболее удобных и надежных. Однако до сих пор её практическое применение было затруднено из-за сложного процесса расчета координационных чисел ( Z) и отсутствия молярных объемов в жидком состоянии (V j^ ) некоторых компонентов (например, С, Ta, V 2 O 5 , Cu 2 S, CaSiO 3 ). Упрощение MIVM достигнуто путем придания обоим Z i и Z j значений, равных 10, и заменой молярного объема i -компонента в жидком состоянии на его молярный объем в твердом состоянии ( V i ) [13–16].

При расчете VLE коэффициент активности компонента в жидкой фазе является существенным параметром. Согласно MIVM, молярный избыток энергии Гиббса G:^ жидкой смеси i-j мож- но представить как:

G m      j (

— = X; ln

ЯГ ⁱ \

______ Vmi ______\ + x . In (______ ^V ™-, ______^ _— ^X i ^X j ( ^Z i ^BpnB jl । ^z j ^B lj^ ^nB lj X l V _m i +X j V _m j Bji) ^' X^j^ j mmj+XimjBiljij/ 2 \ Xi +X j ^B ji X j +X i ^B ij

),                 (6)

где x_i и x j ‒ молярные доли i- и j -компонентов; Z _i и Z j ‒ первые координационные числа; V_mi и V_m j ‒ молярные объемы i- и j -компонентов в жидкой фазе; B_i j и B j _i ‒ параметры потенциальной энергии парного взаимодействия (уравнение (7)); R ‒ универсальная газовая постоянная.

Значения B ij и B ji из уравнения (6) определяются выражениями:

где k – константа Больцмана; ε ij , ε ii и ε jj – потенциальные энергии парного взаимодействия i–j , i–i , j–j систем, где ε ij = ε ji [17–20].

Координационное число определяли следующим образом:

=

tV2^ / r^; |_L

3   ^mi ^_^ oi

') Р^ехр

/ ^H mi ^(T mi ^T) к Z _c RTT mi

),

где p_t = N i /V i = 0,6022 - молекулярная плотность; V i - мольный объем и N i - число молекул; ^H_m i - энтальпия плавления; Т_т 1 - температура плавления; Z c = 12 - координационное число плотной упаковки; Т – температура жидкого металла, К; R – газовая постоянная; r оi = 0,918 d covi – доля атомного ковалентного диаметра ( d covi ); r mi = σ i , где σ i – атомный диаметр.

Для бинарной смеси i-j с помощью термодинамического соотношения (dG m /dx i ) T , p , x , ^ i , коэффициенты активности i- и j- компонентов могут быть получены из уравнения (6) соответственно как :

l = ln f      ^у тл     ) + _x. f     ^y mj ^Bji^y mi ^B j    ) _ x j [ ^Z i ^B ji ^lnB ji + ^Z j ^B>^B ij "

• ¹         \^xi ^y m, i ^^ j ^y mj ^B ji)     ⁷ \^xi ^y m, i ^^ j ^y mj ^B ji     ^x j ^y m,j ^+x i ^y m,i ^B ij /     ² [^(x i ^+x j ^B ji ^{)2    (x} у ^+x ^ ^B ^у ⁾²

Iny. = ln f----^----A + X i f--- ^ymBjymBj--- A _ ^\ ^{Z j B}>^Btj₂ + ^{Z i B}>^{B j}a (10)

• ^{7        Xx}j^ym+^xxi^ym,i^Bij/       ^Xxj^ym,j^xxi^ym,i^Bij   ^xi^ym,i^+xj^ym,j^Bji/    ² [(Х у +Х ^ У ^у )      (X^+XjBjf) J

Необходимые двоичные параметры B_i j и B j _i могут быть рассчитаны из уравнений (10) и (11) с помощью метода Ньютона – Рафсона, если коэффициенты активности бесконечного разбавления, а именно: y ^ и y ^ , бинарных жидких сплавов и соответствующие параметры их компонентов ( V mi и Z i ), доступны.

Значения B ij и B ji при любой температуре могут быть рассчитаны из уравнения (11) предполагая, что -С^^) и -( ^£;\^£“ ) в уравнении (7) не зависимы от температуры:

.

T( 1)/ T (2)                       T (1)/ T (2)

B ij (2) = B ij (1)         ; B ji (2) = B ji (1)

Координационное число Z i жидких металлов может быть рассчитано из уравнения (8), однако это несколько сложнее, поскольку ряд параметров, включая молекулярные объемы для некоторых компонентов, отсутствует в литературе. Следовательно, упрощение MIVM необходимо для расширения области его применения, поскольку метод прогнозирования, включающий только некоторые параметры, является необходимым.

Фактически в решеточной теории растворов Z имеет одно и то же постоянное значение между 6 и 12. Кроме того, Z ≈ 10 для типичных жидкостей в обычных условиях. Установлено, что разница между координационными числами компонентов незначительно влияет на точность прогнозирования MIVM. Однако лучшие результаты получены, когда Z близко к 10. Таким образом, в целях упрощения MIVM значения Zi и Zj могут быть равны 10. Кроме того, молярный объем i-компонента в жидком состоянии Vmi может быть заменен его молярным объемом в твердом состоянии Vi, поскольку разность плотностей для вещества между жидким и твердым состояниями небольшая, то уравнение (7) можно упростить:

^в т i / — = X[ ln ■ RT ¹ V

y i

^x i ^y i ^+x j ^y j ^B ji

)

,     , /      yj      A r       /B ji lnB ji     B ij lnB ijX

+ X,- In ---------- _ 5x j Xi —--- — +— ---- .

^J    V ^x j ^y j ^+x i ^y i ^B ij/         ⁷ \^xi ^+x j ^B ji    ^x j ^+x i ^B ij/

Уравнения (9) и (10) также можно упростить до следующего вида:

InY i = 1 + ln

y i ^x i ^y i ^+x j ^y j ^B ji

)_f

x i y i ^x i ^y i ^+x j ^y j ^B ji

,      X j^yi ^B ij   )

X j y j +X i y i B ij)

_ 5_X 2 f ^B>^B ji + ^B>^B ij )

⁷ \^(x i ^+x j ^B ji ^{)2     (x} j ^+x i ^B ij) ² /,

Iny, = 1 + ln f---- ^Уу ----) - f--- ^{X j y} ---+    ^{X i y j B ji}  ) - 5x 2 f ^Bv^lnBij  ₊   ^{B ji lnB ji} )

⁷              \^x j ^y j ^+x i ^y i ^B ij/     \ ^x j ^y j ^+x i^yi ^B ij     ^x i ^y i ^+x j ^y j ^B ji/         ¹ '^Xy+i^xxi.¹³lf)^{2    (x} i ^+x j ^B ji ⁾² /

Уравнения (13), (14), относящиеся к SMIVM , не содержат координационного числа чистого компонента, что делает эту модель более удобной, по сравнению с MIVM [21–26].

Давление насыщенных паров чистых компонентов, необходимое для расчета VLE , может быть получено следующим образом:

lg p^sat = AT ^‒1 + B lg T + CT + D ,                                                            (15)

где p^sat ‒ давление насыщенных паров чистого компонента, Па; T ‒ абсолютное значение температуры, К; коэффициенты A - D являются константами испарения.

Для проверки адекватности расчетных значений содержания компонентов сплавов в жидкой и газовой фазах сравнили их с экспериментальными данными. Для этого были вычислены показания среднего относительного отклонения (5 ; , %) и среднего квадратичного отклонения (5 j , мольные доли):

5 = ± too Zp_ |x(y)i,e.p-x(y)i,cai| _ 100 %, (16) ; П 1-1 | X(y)i,exp | г -1210,5

П ^ -А^Хехр - ^x(y) i,cal \ J , ⁽¹⁷⁾ где x ( y ) i , exp и x ( y ) i , cal – экспериментальные и расчетные значения содержания мольных долей компонента i в жидкой ( х ) и газовой ( у ) фазах соответственно; n – количество экспериментальных данных.

Методика исследований

Образцы сплавов Hg–Se для эксперимента массой 50–100 г каждый были подготовлены с использованием чистых ртути и селена (99,99 мас. %). Навески исходных металлов были проплавлены в индукционной печи в атмосфере аргона высокой чистоты для получения Hg–Se сплавов состава Hg/Se, мол. %: 20/80; 30/70; 40/60; 50/50; 60/40; 70/30; 80/20.

Лабораторные эксперименты по дистилляции компонентов сплавов проводились в вертикальной вакуумной печи. Давление в печи во время эксперимента составляло Р = 1,33–133 Па, температура Т = 823–1073 К. Состав образцов возгонов и остатков определяли из предварительно полученных растворов атомно-абсорбционным методом на установке GBC 933 АВ Plus . В экспериментах использовали образцы сплавов цилиндрической формы. Сначала образец помещали в цилиндрический тигель ( h = 40 мм, d = 40 мм) из тонкодисперсных зерен графита высокой плотности. Затем тигель переносили в вакуумную печи и нагревали, контролируя температуру. Для предотвращения испарения ме-

таллов на стадии плавления образца процесс осуществляли в атмосфере аргона при нормальном давлении. Разряжение в рабочей камере производили паромасляным диффузионным насосом при достижении необходимой температуры – этот момент считали началом вакуумной перегонки ( t = 0). Затем поддерживали в камере давление и температуру в течение заданного времени эксперимента. По окончании опыта выключали обогреватель, аргон заполнял камеру, давление в которой нормализовалось. Компоненты сплавов, перешедшие в возгоны, конденсировались на холодной пластине, подключенной к циркуляционной водной системе. При температуре 40 °С возгоны и остаток вынимали из печи и взвешивали.

Результаты и их обсуждение

Исходные характеристики Hg–Se сплава приведены в табл. 1.

Ртуть более легко возгоняется (p Hg = = 1,4·10⁴–3,7·10⁵ Па) по сравнению с селеном (P se = 1.3^10 8 3.5^Ю 4 Па), который преимущественно концентрируется в жидкой фазе, что позволяет их разделить вакуумной дистилляцией до определенной степени (табл. 2). Возможность отделения Hg от Se из их сплава вакуумной дистилляцией характеризуется коэффициентом разделения (β), для расчета которого используют коэффициенты активности (табл. 3, 4).

Значения β Hg > 1, поскольку cодержание Hg в газовой фазе больше, чем в жидкой ( у Hg >>  x Hg ). Ртуть концентрируется в газовой фазе, селен – в кубовом остатке ( x Se >>  у Se ), что разделяет исходный сплав Hg–Se на ртуть и селен. Коэффициент разделения ртути и селена возрастает (lgβ Hg = 1,0–2,73) по мере снижения температуры процесса (1073–823 К) и доли селена ( x Se = 0,9–0,1) в составе бинарного сплава (рис. 1).

Таблица 1

Значения параметров у " , у " , B _tj , B _jb Z _t , Z j , p j , p j , V m ( i, ) сплава Hg-Se

Table 1

Parameter values у " , у " , B_u , B j _t , Z _t , Z j , p ^ , p j , V m y, ) alloy Hg-Se

i–j сплав	Т , К	∞ ∞ Y Hg /Y Se		В		Z
				SHg-Se	SSe-Hg	Hg	Se
Hg/Se	705	0,398/0,482		1,0762	1,2714	10	10
Металл	–А	–В	С	D	V m = f ( T ), см3/моль
Hg	3066	–	–	9,877	15,3[1 + 1,9·10‒4( T ‒ 752,9)]
Se	4990	–	–	10,214	16,2[1 + 2,1·10–4( T – 773,4)]

Таблица 2

Рассчитанные давления паров Hg и Se

Table 2

Calculated vapor pressures Hg and Se

Т , К	P Hg , Па	P se , Па	P Hg /P se
823	1,418·106	1,415·104	100,21
923	3,591·106	6,423·104	55,91
1023	7,585·107	2,169·105	34,97
1073	1,046·107	3,66·105	28,58

Таблица 3

Рассчитанные значения коэффициентов активности Hg и Se в расплаве

Table 3

Calculated values of the activity coefficients Hg and Se in the melt

T , К	γ	x Hg
		0,1	0,3	0,5	0,7	0,9
823	γ Hg /γ Se	0,253/0,984	0,415/0,855	0,621/0,629	0,833/0,380	0,978/0,181
923		0,295/0,985	0,460/0,870	0,658/0,666	0,853/0,430	0,981/0,227
1023		0,334/0,987	0,499/0,883	0,689/0,696	0,868/0,473	0,984/0,270
1073		0,352/0,988	0,516/0,888	0,702/0,709	0,875/0,492	0,984/0,291

Таблица 4

Рассчитанные значения коэффициента разделения Hg и Se ( lgβ_Hg )

Table 4

Calculated values of the separation coefficient Hg and Se ( lgβ Hg )

T , К	x Hg	0,1	0,3	0,5	0,7	0,9
823	lgβ Hg	1,411	1,687	1,995	2,342	2,733
	lg у Se	‒0,587	‒1,339	‒2,0	‒2,71	‒3,688
923	lgβ Hg	1,224	1,471	1,742	2,045	2,383
	lg у Se	‒0,456	‒1,136	‒1,750	‒2,415	‒3,338
1023	lgβ Hg	1,073	1,296	1,539	1,807	2,105
	lg у Se	‒0,365	‒0,976	‒1,552	‒2,178	‒3,060
1073	lgβ Hg	1,008	1,22	1,452	1,706	1,985
	lg у Se	‒0,329	‒0,909	‒1,467	‒2,078	‒2,940

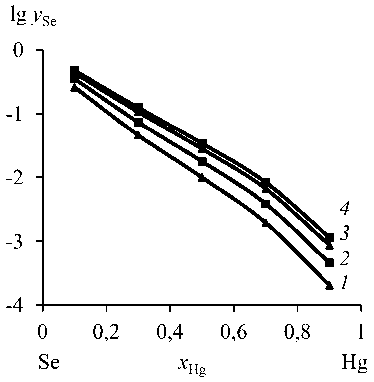
Рис. 2. Cодержание Se в возгонах при температуре, К: 823 ( 1 ); 923 ( 2 ); 1023 ( 3 ); 1073 ( 4 )

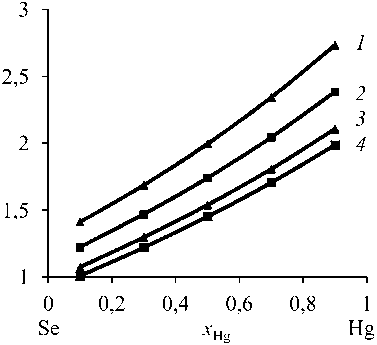
Рис. 1. Коэффициент разделения селена при вакуумной дистилляции Hg–Se сплава при температуре, К: 823 ( 1 ); 923 ( 2 ); 1023 ( 3 ); 1073 ( 4 )

Fig. 1. Selenium separation coefficient during vacuum distillation of Hg–Se alloy at temperature, K: 823 ( 1 ); 923 ( 2 ); 1023 ( 3 ); 1073 ( 4 )

Fig. 2. Selen content in sublimations at a temperature, K: 823 ( 1 ); 923 ( 2 ); 1023 ( 3 ); 1073 ( 4 )

Таблица 5

Данные по количественному составу продуктов дистилляции представлены на рис. 2 и в табл. 4, 5. Ртуть можно отделить от селена возгонкой при температуре ≤ 550 °С. Исходя из состава сплава ( x Se ) можно прогнозировать температуру, при которой количество возгоняемой примеси селена в конденсированной ртути не будет превышать заданную величину: для x Se (ат. %/мас. %), равного10/4,2, при 550 °С значение у Se (ат. %/мас. %) составляет 2,15·10^–4/0,9·10^–4, а для 800 °С ‒ у Se (ат. %/мас. %) достигает 11,48·10^–4/4,82·10^–4. В этом случае при увеличении температуры возгонки на 250 °С содержание селена в Hg-конденсате возрастает в ~ 5 раз.

Активности Hg и Se ( a Hg , a Se ) в расплаве определены с использованием рассчитанных значений коэффициентов активности этих компонентов (γ Hg , γ Se ) (рис. 3, табл. 3).

При построении « Т – х » диаграммы бинарной системы Hg–Se для каждой фиксированной температуры подбирали состав сплава ( х Hg ), при котором сумма парциальных давлений ртути и селена уравнивала внешнее давление (табл. 6, рис. 4 а ).

Установлено, что при увеличении глубины вакуума переход из жидкой в газовую фазу происходит в более узком диапазоне температур и способствует разделению Hg и Se, а именно: для получения конденсата ртути c возгонкой 90‒99 % элемента при давлении 133/13,3/1,33 Па и температуре 527‒598/460‒524/408‒464 К содержание примеси селена составит не более 0,553/0,369/0,224 мольных долей, что свидетельствует о благоприятном воздействии низкого остаточного давления в системе и, соответственно, температуры процесса на селективность при задан-

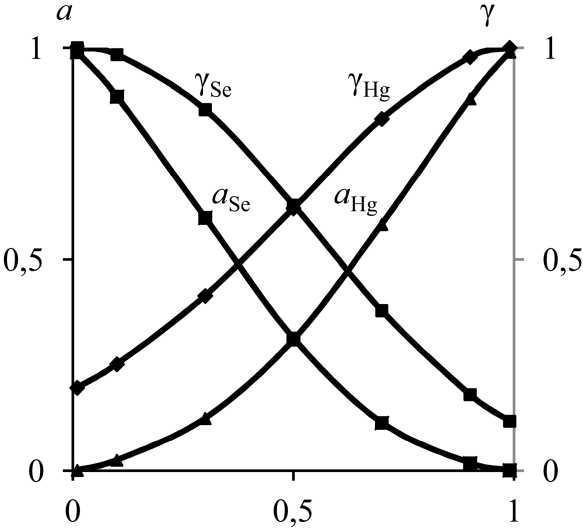
Рис. 3. Активности ( а ) и коэффициенты активности ( γ ) компонентов Hg–Se сплава при 823 К

Fig. 3. Activity ( а ) and activity coefficients ( γ ) of Hg–Se alloy components at 823 K

Рассчитанные значения lg у _Se сплавa Hg–Se

Table 5

Calculated values of lg у Se Se of Hg–Se alloy

T , К	x Hg	0,01	0,03	0,05	0,07	0,09
823	γ Hg /γ Se	0,197/1,0	0,208/0,999	0,220/0,996	0,233/0,992	0,246/0,987
	lg у Se	‒0,079	‒0,216	‒0,335	‒0,443	‒0,540
923	γ Hg /γ Se	0,236/1,0	0,248/0,999	0,261/0,996	0,274/0,993	0,288/0,988
	lg у Se	‒0,054	‒0,155	‒0,248	‒0,335	‒0,417
1023	γ Hg /γ Se	0,272/1,0	0,285/0,999	0,298/0,997	0,312/0,994	0,326/0,989
	lg у Se	‒0,040	‒0,117	‒0,190	‒0,262	‒0,330
1073	γ Hg /γ Se	0,289/1,0	0,303/0,999	0,316/0,997	0,330/0,994	0,345/0,990
	lg у Se	‒0,035	‒0,103	‒0,169	‒0,234	‒0,298

Таблица 6

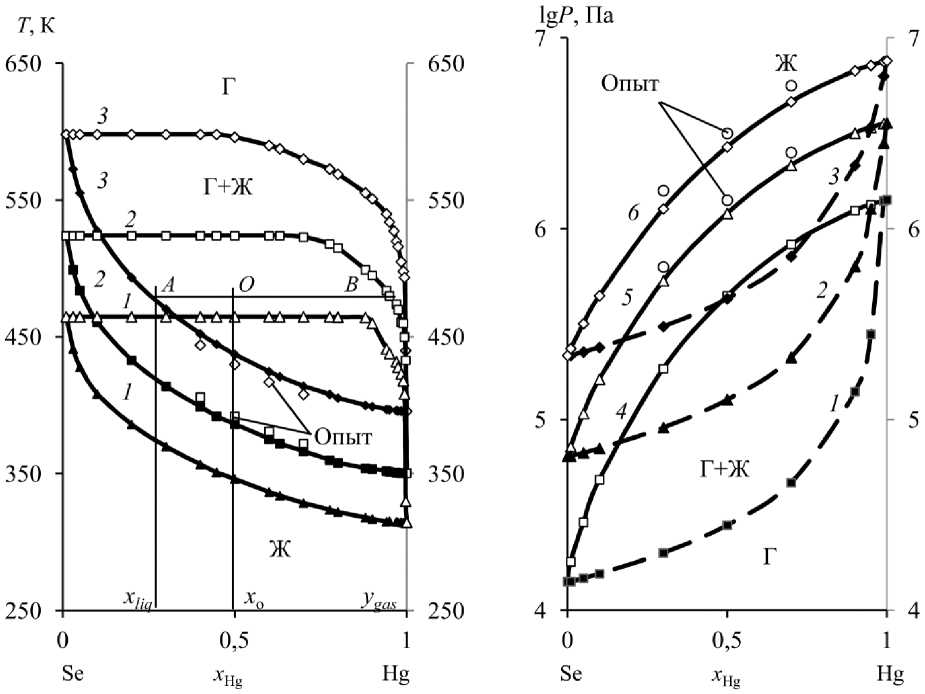
a)

b)

Рис. 4. Фазовые диаграммы « Т – х » ( а ) и « Р – х » ( b ) Hg–Se сплава при Р , Па:

1,33 ( 1 ); 13,33 ( 2 ); 133,3 ( 3 ) и Т , К: 823 ( 4 ); 923 ( 5 ); 1023 ( 6 )

Fig. 4. Phase diagrams of “ Т – х ” ( а ) and “ Р – х ” ( b ) Hg–Se alloy at P , Pa: 1,33 ( 1 ); 13,33 ( 2 ); 133,3 ( 3 ) and T , K: 823 ( 4 ); 923 ( 5 ); 1023 ( 6 )

ной степени возгонки ртути. Одновременно в кубовом остатке в указанных интервалах давления и температуры содержание селена возрастает на те же 90‒99 % металла.

Определены значения относительного (S i = 1,34 %) и квадратичного (S ^ = 6,82 К) отклонений между вычисленными и опытными значениями температур Т = 823‒1023 К и давлений Р = 1,33‒133,3 Па (рис. 4). Было получено порядка 20 экспериментальных значе-

ний температур плавления при различных давлениях в системе (рис. 4 а ) и столько же опытных значений давления при различных температурах (рис. 4 b ). Относительно невысокие абсолютные значения вычисленных средних отклонений свидетельствуют об адекватности модели процесса вакуумной дистилляции бинарного сплава в исследованных интервалах изменения давления ( Р ) и температуры ( Т ).

Рассчитанные значения T liq , у Se Hg–Se сплавa для « Т – х » диаграмм

Table 6

Calculated values of T liq , у Se Hg–Se alloy for “ Т – х ” diagrams

P , Па	x Hg	0,01	0,03	0,05	0,10	0,90	0,95	0,99
133	Т liq , К	598,1	572,7	555,3	527,5	399,1	396,9	395,7
	y Se	0,553	0,231	0,120	0,0374	341,56·10‒10	66,24·10‒10	5,956·10‒10
13,3	Т liq , К	524,2	499,1	484	460,8	353,4	351,6	350,45
	y Se	0,369	0,120	0,057	0,0159	300,35·10‒11	41,93·10‒11	3,26·10‒11
1,33	Т liq , К	464,8	441,3	428	408,4	317,1	315,4	314,5
	y Se	0,224	0,059	0,025	0,0065	239,38·10‒12	25,21·10‒12	1,43·10‒12

Таблица 7

Таблица 8

Для фазовых диаграмм VLE может быть использовано правило рычага (правило отрезков) для прогнозирования количества вещества, остатков и возгонов при заданной температуре. Предполагая, что мольная доля Hg в сырье сплава х о = 0,5, соответствующая температура перегонки 480 К и давление 133 Па, по правилу «рычага» может быть построена линии связи АВ на « Т – х » диаграмме (рис. 4 а ), где кривые жидкости и пара пересекаются в точке А и В соответственно. Когда система достигает равновесия, составы А и В равняются х liq и y gas соответственно. По правилу рычага можно получить:

Пи д _ X ₀ -y _gas _ |0S| = 0,5-0,999 = 0,499

nqas "" Xltq-Xo - |ОЛ| 0,25-0,5    0,25 , где nliq = 0,499 и ngas = 0,25 – количество вещества в остатках и возгонах; |0S| и |0А| -

длина соответствующих отрезков на линии AB . Общее количество молей вещества ис-

ходного сплава n , то n = n liq + n gas :

Xo-Vgas      |OS|0,499

Ицп _----—И _ -—"И =И

"''   XUq-ygas      |ЛВ|0,749

0,666 n ,

^И даз ^_

Xliq-Xo       |ОЛ|0,25

—----И _ -—-и =И

Xltq-Vgas      i^Bj0,749

0,334 n .

Результаты расчета диаграмм « Р – х » представлены на рис. 4 b , табл. 7, 8.

Диаграмма « Р – х » позволяет прогнозировать процесс дистилляции Hg–Se сплава по-

средством изменения величины остаточного давления в системе при фиксированной температуре. Например, при температуре 823 К и давлении Р gas = 1,4·10⁵ Па равновесное содержание селена в Hg-возгонах/Se-остатке равняется 0,1/0,756 мольной доли. При повышении температуры до 1023 К аналогичный состав газовой фазы (Hg/Se = 0,9/0,1) сохраняется при более высоком давлении ( Р gas = 21,47·10⁵ Па) и уменьшении содержания селена в кубовом остатке до ~ 0,58 мольных долей. В целом, данные « Р – х » диаграмм дополняют сведения « Т – х » диаграмм для бинарного сплава Hg–Se.

Изменение энергии Гиббса ДС Щ для бинарной смеси Hg–Se, определяется процессом удерживания вещества в пограничном слое фаз при переходе «жидкость – газ», обусловленном соотношением компонентов в сплаве и температурой системы (рис. 5, табл. 9).

Величина изменения энтальпии пограничного слоя (АН щ ) определяется энергией Гиббса и теплотой образования поверхности (ТА5:Щ ), где А5, Щ - изменение энтропии. Отрицательные значения изменения энтальпии АН Щ < 0 свидетельствуют об экзотермическом процессе дистилляции компонентов Hg–Se сплава. Небольшие абсолютные значения из-

Рассчитанные значения Р liq ·10⁵ (Па) Hg–Se сплавa

Table 7

Calculated values Р_liq ·10⁵ (Pa) Hg–Se Alloy

Т , К	x Hg
	0,1	0,3	0,5	0,7	0,9
823	0,484	2,729	4,446	8,279	12,47
923	1,629	5,346	12,02	21,53	31,70
1023	4,457	12,71	26,85	46,34	67,30

Значения у Hg , P gas (Па), γ Hg , γ Se = 1,0 для « Р – х » диаграмм Hg–Se сплава

Table 8

Values of у Hg , P gas (Pa), γ Hg , γ Se = 1,0 for “ Р – х ” diagrams of Hg–Se alloy

T , К	y Hg	0,1	0,3	0,5	0,7	0,9
823	x Hg ·10–3	5,661	20,86	45,33	92,97	244,33
	γ Hg	0,194	0,203	0,218	0,248	0,364
	P gas ·104	1,557	2,001	2,802	4,67	14,01
923	x Hg ·10–3	8,372	30,60	65,35	130,3	327,2
	γ Hg	0,235	0,248	0,271	0,317	0,487
	P gas ·104	7,065	9,084	12,72	21,19	63,58
1023	x Hg ·10–3	11,52	41,55	87,37	170,68	419,02
	γ Hg	0,273	0,292	0,324	0,387	0,608
	P gas ·104	23,86	30,67	42,94	71,57	214,7

Значения изменения термодинамических параметров Hg–Se сплавa

Values of changes in the thermodynamic parameters of the Hg–Se alloy

Таблица 9

Table 9

T, К -AG-^, кДж/моль xSe 0,1 0,3 0,5 0,7 0,9 823 1,124 2,567 2,997 2,475 1,045 923 0,989 2,266 2,652 2,195 0,928 1023 0,883 2,028 2,379 1,973 0,836 1073 0,838 1.927 2.262 1.877 0,796 - АН^, кДж/моль 2,057 4,655 5,395 4,426 1,856 - AS'„, Дж/моль^К 1,143 2,56 2,939 2,39 0,994 уменьшении содержания селена в кубовом остатке до ~ 0,58 мольных долей.

3. Равновесные диаграммы « Т – х » и « Р – х » для систем Hg–Se можно использовать, в частности, на предварительных этапах проектирования опытно-промышленного обо-

рудования для вакуумной дистилляции, а также для обоснования выбора диапазонов температуры и давления в системе с целью получения продуктов возгонки необходимого состава, минимизируя количество трудоемких и дорогостоящих установочных опытов.