Фазовые равновесия в системе Pb-Ag при пирометаллургической возгонке
Автор: Королев Алексей Анатольевич, Краюхин Сергей Александрович, Мальцев Геннадий Иванович
Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy
Рубрика: Физическая химия и физика металлургических систем
Статья в выпуске: 2 т.17, 2017 года.
Бесплатный доступ
При переработке свинца образуется серебристая пена (СП), требующая комплексной переработки с получением товарных моноэлементных продуктов. Одним из возможных способов рекуперации СП является вакуумная перегонка, считающаяся одним из самых эффективных и экологически чистых методов для разделения и очистки, переработки и рафинирования различных металлов. Для предварительного выбора температуры и давления системы, оценки эффективности разделения компонентов при вакуумной перегонке используют фазовые диаграммы. Цель работы состоит в расчете равновесных состояний «газ - жидкость» VLE (vapor liquid equilibrium), включая зависимости состава фаз от температуры (Т-х) и давления (р-х) для Pb-Ag сплава при вакуумной перегонке на основе модели MIVM (мolecular interaction volume model). В интервале температур 1073-1773 К рассчитаны давления насыщенного пара для Pb (1,5.10-1-4,86•102) и Ag (5,1•10-5-6,6). Высокие значения соотношения р*Pb / р*Ag = = 2,9•103-74 и коэффициента разделения βPb = 1,8-3,9 создают теоретические предпосылки для селективного выделения этих металлов вакуумной дистилляцией, когда свинец обогащается в газовой фазе (βPb > 1), а серебро - в жидкой. Мольная доля свинца в газовой фазе уPb = 0,878-0,999 увеличивается с ростом температуры 1073-1773 К и мольной доли металла в сплаве хPb = 0,1-0,9. С использованием модели MIVM рассчитаны коэффициенты активности свинца γPb = 0,474-0,999 и серебра γAg = 0,331-0,999 для Pb-Ag сплава различного состава в исследованном температурном диапазоне. Для фазовых диаграмм VLE может быть использовано правило рычага (правило отрезков) для прогнозирования количества вещества, остатков и возгонов при заданной температуре. Для границы раздела фаз «жидкость - газ» Pb-Ag сплава определены значения избыточных энергии Гиббса, энтальпии и энтропии: GmE = 0,01-1,34 кДж/моль; -HmE = 0,32-1,53 кДж/моль; SmE = 0,52-1,65 кДж/моль•К. Фазовые диаграммы VLE сплавов обеспечивают необходимой информацией для проектирования технологических параметров промышленного производства вакуумной металлургии, а также для прогнозирования необходимого состава Pb-Ag сплава в зависимости от температуры и давления в процессе вакуумной перегонки.
Равновесная фазовая диаграмма, вакуумная дистилляция, молекулярная объемная модель взаимодействия
Короткий адрес: https://sciup.org/147157152
IDR: 147157152 | УДК: 661.85:669.053:66.048.1-982 | DOI: 10.14529/met170203
Текст научной статьи Фазовые равновесия в системе Pb-Ag при пирометаллургической возгонке
Вакуумная перегонка считается одним из самых эффективных и экологически чистых методов для разделения и очистки, переработки и рафинирования различных металлов. Она имеет ряд преимуществ, таких как относительно низкое потребление энергии, короткий производственный цикл, высокую рентабельность, отсутствие подлежащих утилизации отходов по сравнению с традиционными методами, например, пирометаллургической переработкой и электролизом [1–4].
Равновесные фазовые диаграммы «жидкость – газ» (vapor liquid equilibrium – VLE), включая зависимости состава от температуры (Т–х) и давления (р–х), рассчитаны для Pb–Ag сплава при вакуумной перегонке на основе модели VLE и молекулярной модели объемного взаимодействия (мolecular interaction volume model – MIVM). Объективные VLE зависимости важны для выбора температуры и давления системы, оценки эффективности разделения в вакуумной перегонке. Определение термодинамических характеристик из экспериментальных данных занимает много времени и требует значительных финансовых затрат. Следовательно, теоретический расчет является альтернативным и эффективным способом получения информации о термодинамических свойствах сплавов, особенно для многокомпонентных систем [5–8].
Методика исследований
В равновесной системе «жидкость – газ» химический потенциал (фугитивность) каждого компонента в обеих фазах равен и соответствует зависимости [9]:
ф; РУ ; = Ф ^ P ^' Y i X i exP С1^0 ), (1) где Ф ; - фугитивность компонента i в газовой фазе; Ф ; - коэффициент фугитивности насыщенной жидкости чистого компонента i ; T и p – температура и давление в системе; pt * - давление насыщенных паров чистого компонента i при температуре T ; y ; — коэффициент активности компонента i в жидкой фазе при данных температуре, давлении и мольной доли компонента i ; х i и у i – мольная доля компонента i в жидкой и газовой фазах, соответственно; V [ - мольный объем чистой жидкости i; R - универсальная газовая постоянная.
Остаточное давление в исследуемой системе достаточно низкое ( р ≤ 133 Па) и паровая фаза ведет себя как идеальный газ, откуда Ф ; = Ф i ~ 1,0, а экспоненциальный член exp (V (PRTPi^ ) ~ 1. Таким образом, уравнение (1) можно упростить, подобно модифицированному закону Рауля [9]:
версальная газовая постоянная, а потенциальные энергии парного взаимодействия B ij и B ji определяются следующим образом:
By = expV-C-^l B ji =
= ехр\ ( J. )] (8) где k – константа Больцмана; ε ij , ε ii и ε jj – потенциальные энергии парного взаимодействия i – j , i – i , j – j систем, где ε ij =ε ji .
Для бинарной смеси i – j , с помощью термодинамического соотношения (д GEm/дx i ) T , p , x; , коэффициенты активности компонентов i и j могут быть получены из уравнения (7), соот-
ветственно, как:
InY ; = ln (
+xj (
—
V m,i
. Xi V m,i +x j V m,j B ji
V m,j B ji
—
■) +
V mi B ij
X i V m,i +X j V m,j B ji X j V m,j +X i V m,i B ij
■)—
Ру; = PiYiXi.(2)
Если жидкая смесь является идеальным раствором, то γ i = 1 в (2).
Для бинарного сплава i – j справедливо:
xi + xj = 1, yi + yj = 1;(3)
Р = P t YtXt + P j Y j X j =
= PtYiXi+ pjYj(1-Xi).(4)
lnY j = ln (
+x ; (:
Xi 2 г
2 I
V mj
,x jV m,j +x i V m,i B i j.
V mi B ij
—
■) +
V mj B ji
. Xj V m ,j +X i V mi B ij X i V m,i +X j V m,j B ji
- Zj B ij- lnB ij + Z i B ji lnB ji ]
- ( Xj+XiBij )2 ( Xi+XjBji )2
■)—
Объединяя уравнения (2) и (4), получим
Когда x i или x j в приближаются к нулю, коэффициенты активности бесконечно разбавленных растворов yT и y^ являются про-
выражения для хi и уi :
*
r = P—P j Y j ;
; P i Y i —P j Yj’
изводными из уравнений (9) и (10) щим образом:
следую-
У ; =
* P i Y i ^ i
.
P
lnY T =i—ln( V m?)—
V mi B ij V mj
—
Коэффициенты активности компонентов в жидкой фазе имеют решающее значение для расчета фазовой диаграммы VLE . Модель MIVM [10] считается одной из наиболее удобных и надежных моделей [11–13]. Согласно
— 2 (^ i lnB ji + ZjBij^nBij );
1 oo -1 i (Vm,iBij\ lnYj =1—lnl^-
— 2 ( Zj^nBij + ZiBji l nBji ).
V mj B ji V mi
—
MIVM молярная избыточная энергия Гиббса G m для границы раздела фаз «жидкость - газ» смеси i – j может быть выражена как
^ = xt ln ( ---^---) +
RT ; \xt^mi+x:j^njBjlJ
Необходимые двоичные параметры B ;j и B ji можно рассчитать из уравнений (11) и (12) по формуле Newton [10] если известны коэффициенты активности для бесконечно разбавленных растворов, т. е. yT и Y j бинарных
+X j In
V mj X j V mj +X i V mi B ij
)-
—
X i X j (ZiB jii^Bj t + Z j B ij\ ^B ij ) 2 X i +X j B ji X j +X i B ij ,
жидких сплавов и соответствующие параметры их компонентов [14, 15]. Координационное число Z i жидких металлов рассчитывают как [10]:
где x i и x j – молярные доли; Z i и Z j – координационные числа; V mi и V mj – молярные объемы компонентов i и j , соответственно; R – уни-
Z„ 4У 2 Л / ^ mi Toi \
3 Vrm[—r0[/
X
, ЛНт1(Тт1—Т\
X P i r mi exp ( mRTmi ), (13)
Z c R1 Т mi
где р ; = N i / V i - молекулярная плотность; Vi – мольный объем и Ni – число молекул; ДН т; - энтальпия плавления; Тт ; - температура плавления; Z c = 12 – координационное число плотной упаковки, Т – температура жидкого металла, K ; R – газовая постоянная; r 0 i = 0,918 d covi – доля атомного ковалентного диаметра ( d covi ), который подразумевает, что длина ковалентной связи образуется путем обмена внешних валентных электронов с другими атомами элемента при подходе на наименьшее расстояние между соседними атомами; r mi равняется, примерно, атомному диаметру σ i ( r mi = σ i ).
Значения B ^j и B j; при требуемой температуре ( Т 2 ) можно получить из уравнения (8) для известных значений B ;j и B j; при температуре ( Т 1), принимая независимой от температуры потенциальную энергию парного взаимодействия компонентов — EiJ E jj и к
-
— Jik “ . Например, в бинарной системе Pb-Ag при Т 1 = 1300 B ij / B ji = 0,5974/1,445, тогда для Т 2 = 1273:
-
- У^ = TlnB;j = 1300.ln(0,5974) =
= –669,719 К;
B ;j = exp(-669,719/1273) = 0,5910;
-
- (E ij — E jj ) = -0,058 э-в;
-
— ^^ = n nB j; = 13001n(1,445) =
= 478,542 К;
B j; = exp (478,542/1273) = 1,456;
-
- (E ji — E ;; ) = 0,041 э-в.
Давление насыщенных паров чистых компонентов рассчитывают [16]:
lg p* = AT –1 + B lg T + CT + D , (14)
где p* – давление насыщенных паров чистого компонента, Па; А , B , C , D – константы испарения для компонентов жидких сплавов; Т – абсолютная температура.
Необходимые для расчета параметры Pb–Ag сплава даны в табл. 1.
Для выполнения экспериментальных ис- следований на лабораторной установке вакуумной возгонки были приготовлены Pb–Ag сплавы с переменным содержанием компонентов в диапазоне 0,1–0,9 мольных долей (хij).
Степень разряжения в вакуумной камере во время эксперимента составляла 1,3–133 Па, температура 1073–1773 К, продолжительность (до момента установления равновесия в системе) 2–10 ч. Образцы возгонов и жидкой фазы были получены из конденсата и огарка соответственно. Анализ на содержание свинца и серебра в продуктах дистилляции выполнен из предварительно полученных растворов атомно-абсорбционным методом на установке GBC 933 АВ Plus .
Для того, чтобы проверить адекватность расчетных значений содержания компонентов Pb–Ag сплава в жидкой и газовой фазах, сравнили их с экспериментальные данными. Для этого были вычислены показания среднего относительного отклонения (5 ; ) и среднего квадратичного отклонения (5 ;* ), как показано: 5 = ± too Zp_ | х ( УХе^^ • ioo %, (15) ; П ;-1 X(y) i,exp
[ 1 г -1210,5
п 2 П -1 [^(У) ;,ехр — x(y)t cal \ ] , (16) где x(y) ;,exp и x(y) ;,cai - экспериментальные и расчетные значения содержания компонента i в жидкой и газовой фазах, соответственно; n – количество экспериментальных данных.
Результаты и их обсуждение
Cвинец имеет высокое давление насыщенных паров и легко испаряется в газовую фазу, серебро имеет низкое давление насыщенных паров и остается в жидкой фазе, что создает теоретические предпосылки для разделения этих металлов вакуумной дистилляцией (табл. 2).
Для определения возможности отделения элемента i от элемента j бинарного сплава i–j путем вакуумной дистилляции можно использовать коэффициент разделения β i :
*
Р еь =Р^ . (17)
pAg Y Ag
Таблица 1
Значения у ” , у ” , Вц, В^, Z t , Z , , р * , р * , V m(1,Г) сплава Pb-Ag
|
i–j сплав |
Т , К |
Урь |
У ай |
B Pb-Ag |
B Ag-Pb |
У рь |
^ Ag |
|
Pb–Ag |
1300 |
1,101 |
1,53 |
0,5974 |
1,4450 |
8,91 |
10,61 |
|
Компонент |
А |
В |
С |
D |
V m = f ( T ), см3/моль |
||
|
Pb |
–10130 |
–0,985 |
– |
11,6 |
19,4[1 + 1,24·10–4( T – 600)] |
||
|
Ag |
–14400 |
–0,85 |
– |
11,7 |
11,6[1 + 0,98·10–4( T – 234)] |
||
Таблица 2
Значения β Pb > 1 (рис. 1, табл. 3), поскольку cодержание свинца в газовой фазе больше, чем в жидкой (у Pb » x Pb). Свинец обогащает газовую фазу, а серебро накапливается в жидкой фазе ( x Ag » у Ag ), таким образом, бинарный сплав разделяется на свинец и серебро.
Важно оценить эффект разделения и количественный состав продуктов дистилляции. Эти данные могут быть получены из диаграмм фазового равновесия «жидкость – газ» (рис. 2, табл. 4, 5). Для Pb–Ag сплава, с учетом равенства (3), содержание металлов в газовой фазе равняется:
log Ррь
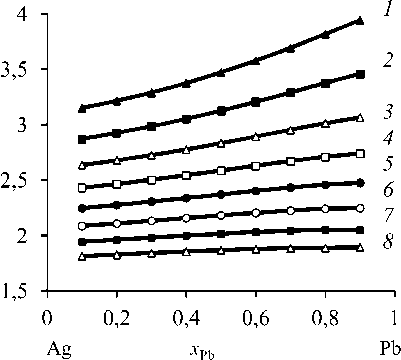
Рис. 1. Коэффициент разделения свинца при вакуумной дистилляции Pb–Ag сплава при температуре, К: 1073 ( 1 ); 1173 ( 2 ); 1273 ( 3 ); 1373 ( 4 ); 1473 ( 5 ); 1573 ( 6 );
1673 ( 7 ); 1773 ( 8 )
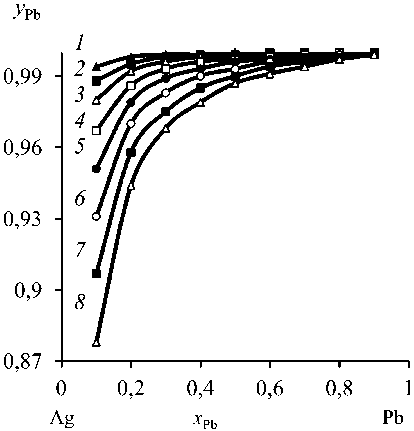
Рис. 2. Зависимость « уРЬ - xPb » Pb-Ag сплава при температуре, К: 1073 ( 1 ); 1173 ( 2 ); 1273 ( 3 ); 1373 ( 4 );
1473 ( 5 ); 1573 ( 6 ); 1673 ( 7 ); 1773 ( 8 )
Рассчитанные давление и соотношение давления паров Pb и Ag
|
Т , К |
р* Pb , Па |
р* Ag , Па |
р * Pb / р * Ag |
|
1073 |
1,49·10–1 |
5,054·10–5 |
2,948·103 |
|
1173 |
8,72·10–1 |
6,53·10–4 |
1,335·103 |
|
1273 |
3,839 |
5,611·10–3 |
6,842·102 |
|
1373 |
1,353·101 |
3,5·10–2 |
3,866·102 |
|
1473 |
4,001·101 |
1,7·10–1 |
2,354·102 |
|
1573 |
1,026·102 |
6,73·10–1 |
1,525·102 |
|
1673 |
2,344·102 |
2,253 |
1,04·102 |
|
1773 |
4,859·102 |
6,558 |
7,409·101 |
Таблица 3
Рассчитанные значения коэффициента разделения ( logpPb ) сплава Pb-Ag
|
x Pb |
1073 К |
1173 К |
1273 К |
1373 К |
1473 К |
1573 К |
1673 К |
1773 К |
|
0,1 |
3,15 |
2,872 |
2,635 |
2,428 |
2,246 |
2,086 |
1,942 |
1,813 |
|
0,2 |
3,215 |
2,926 |
2,678 |
2,463 |
2,275 |
2,108 |
1,96 |
1,827 |
|
0,3 |
3,289 |
2,985 |
2,726 |
2,501 |
2,305 |
2,132 |
1,979 |
1,842 |
|
0,4 |
3,375 |
3,052 |
2,778 |
2,541 |
2,337 |
2,157 |
1,998 |
1,855 |
|
0,5 |
3,472 |
3,126 |
2,834 |
2,584 |
2,369 |
2,181 |
2,015 |
1,868 |
|
0,6 |
3,578 |
3,205 |
2,894 |
2,627 |
2,402 |
2,204 |
2,031 |
1,878 |
|
0,7 |
3,695 |
3,29 |
2,955 |
2,67 |
2,432 |
2,224 |
2,043 |
1,884 |
|
0,8 |
3,82 |
3,376 |
3,013 |
2,708 |
2,457 |
2,24 |
2,05 |
1,889 |
|
0,9 |
3,944 |
3,457 |
3,066 |
2,739 |
2,474 |
2,246 |
2,049 |
1,892 |
Таблица 4
Рассчитанные коэффициенты активности Pb–Ag сплавa
|
T , К |
Y |
x Pb |
||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
||
|
1073 |
Y Pb |
0,474 |
0,534 |
0,6 |
0,672 |
0,748 |
0,822 |
0,89 |
0,948 |
0,986 |
|
Y Ag |
0,991 |
0,962 |
0,91 |
0,837 |
0,746 |
0,641 |
0,531 |
0,424 |
0,331 |
|
|
1173 |
Y Pb |
0,554 |
0,611 |
0,673 |
0,737 |
0,802 |
0,863 |
0,919 |
0,963 |
0,990 |
|
Y Ag |
0,993 |
0,969 |
0,93 |
0,874 |
0,802 |
0,719 |
0,63 |
0,542 |
0,462 |
|
|
1273 |
Y Pb |
0,627 |
0,68 |
0,735 |
0,791 |
0,845 |
0,896 |
0,94 |
0,972 |
0,993 |
|
Y Ag |
0,994 |
0,976 |
0,946 |
0,902 |
0,847 |
0,783 |
0,714 |
0,645 |
0,584 |
|
|
1373 |
Y Pb |
0,691 |
0,739 |
0,787 |
0,835 |
0,881 |
0,921 |
0,955 |
0,980 |
0,995 |
|
Y Ag |
0,996 |
0,982 |
0,959 |
0,927 |
0,885 |
0,839 |
0,788 |
0,740 |
0,700 |
|
|
1473 |
Y Pb |
0,748 |
0,790 |
0,831 |
0,872 |
0,908 |
0,942 |
0,968 |
0,986 |
0,997 |
|
Y Ag |
0,997 |
0,986 |
0,968 |
0,943 |
0,912 |
0,877 |
0,841 |
0,809 |
0,787 |
|
|
1573 |
Y Pb |
0,797 |
0,833 |
0,868 |
0,902 |
0,931 |
0,957 |
0,977 |
0,991 |
0,998 |
|
Y Ag |
0,997 |
0,989 |
0,976 |
0,958 |
0,935 |
0,911 |
0,889 |
0,870 |
0,864 |
|
|
1673 |
Y Pb |
0,839 |
0,870 |
0,899 |
0,927 |
0,950 |
0,970 |
0,985 |
0,994 |
0,999 |
|
Y Ag |
0,998 |
0,992 |
0,982 |
0,969 |
0,954 |
0,939 |
0,927 |
0,921 |
0,928 |
|
|
1773 |
Y Pb |
0,876 |
0,901 |
0,926 |
0,947 |
0,966 |
0,980 |
0,991 |
0,997 |
1,0 |
|
Y Ag |
0,999 |
0,994 |
0,987 |
0,979 |
0,969 |
0,962 |
0,958 |
– |
– |
|
Таблица 5
Рассчитанные значения уРЬ сплава Pb-Ag
log(yAg)
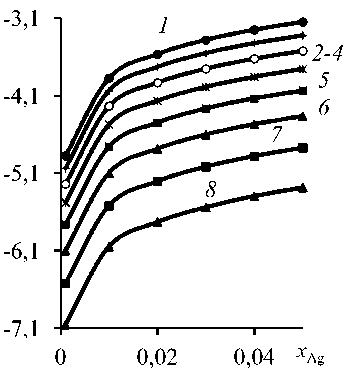
Рис. 3. Зависимость « log(yAg) - xAg » Pb-Ag сплава при температуре, К: 1773 ( 1 ); 1673 ( 2 ); 1573 ( 3 );
1473 ( 4 ); 1373 ( 5 ); 1273 ( 6 ); 1173 ( 7 ); 1073 ( 8 )
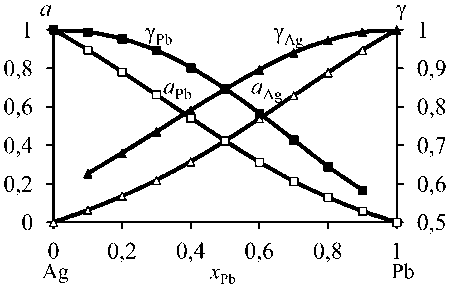
Рис. 4. Активности ( а ) и коэффициенты активности ( у ) Pb и Ag при 1273 К
Таблица 6
Рассчитанные значения yAg • 10 -6 Pb-Ag сплава
|
x Ag |
1073 |
1173 |
1273 |
1373 |
1473 |
1573 |
1673 |
1773 |
|
0,001 |
0,089 |
0,302 |
0,794 |
1,738 |
3,327 |
5,754 |
9,183 |
13,27 |
|
0,01 |
0,899 |
3,046 |
8,017 |
17,54 |
33,61 |
58,06 |
92,63 |
134,0 |
|
0,02 |
1,867 |
6,247 |
16,32 |
35,54 |
67,81 |
117,0 |
186,1 |
272,3 |
|
0,03 |
2,893 |
9,615 |
24,89 |
54,02 |
102,8 |
176,7 |
281,2 |
414,7 |
|
0,04 |
4,014 |
13,15 |
33,84 |
73,07 |
138,4 |
237,5 |
377,6 |
560,9 |
|
0,05 |
5,201 |
16,85 |
43,09 |
92,57 |
174,9 |
299,7 |
475,4 |
707,7 |
Таблица 7
Рассчитанные коэффициенты активности Pb–Ag сплавa
|
x Ag |
||||||
|
T , К |
γ |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
|
1073 |
У рь |
1,0 |
0,999 |
0,999 |
0,998 |
0,997 |
|
Y Ag |
0,263 |
0,270 |
0,276 |
0,284 |
0,291 |
|
|
1173 |
Y Pb |
1,0 |
1,0 |
0,999 |
0,998 |
0,998 |
|
Y Ag |
0,403 |
0,409 |
0,415 |
0,421 |
0,427 |
|
|
1273 |
Y Pb |
1,0 |
1,0 |
0,999 |
0,999 |
0,998 |
|
Y Ag |
0,543 |
0,547 |
0,550 |
0,555 |
0,559 |
|
|
1373 |
Y Pb |
1,0 |
1,0 |
1,0 |
0,999 |
0,999 |
|
Y Ag |
0,670 |
0,672 |
0,674 |
0,676 |
0,678 |
|
|
1473 |
Y Pb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
|
Y Ag |
0,782 |
0,781 |
0,781 |
0,781 |
0,781 |
|
|
1573 |
Y Pb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
|
Y Ag |
0,876 |
0,874 |
0,871 |
0,869 |
0,868 |
|
|
1673 |
Y Pb |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
|
Y Ag |
0,954 |
0,949 |
0,946 |
0,943 |
0,940 |
|
|
1773 |
Y ?b |
1,0 |
1,0 |
1,0 |
1,0 |
1,0 |
|
Y Ag |
0,983 |
0,989 |
0,994 |
0,998 |
0,997 |
|
Таблица 8
Рассчитанные значения yPb , yAg , T liq Pb-Ag сплава для « Т - х » диаграмм
|
P , Па |
x Pb |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
Т liq , К |
1916 |
1824 |
1766 |
1726 |
1694 |
1669 |
1648 |
1630 |
1616 |
|
|
133 |
У рь |
0,919 |
0,916 |
0,924 |
0,937 |
0,954 |
0,969 |
0,983 |
0,993 |
0,998 |
|
Y Ag |
0,999 |
0,995 |
0,987 |
0,974 |
0,958 |
0,938 |
0,918 |
0,900 |
0,893 |
|
|
Т liq , К |
1617 |
1543 |
1499 |
1468 |
1443 |
1423 |
1406 |
1392 |
1381 |
|
|
13,3 |
Y Pb |
0,818 |
0,820 |
0,843 |
0,869 |
0,900 |
0,931 |
0,96 |
0,982 |
0,996 |
|
Y Ag |
0,998 |
0,988 |
0,970 |
0,942 |
0,904 |
0,856 |
0,805 |
0,750 |
0,701 |
|
|
Т liq , К |
1399 |
1340 |
1305 |
1279 |
1259 |
1242 |
1228 |
1217 |
1207 |
|
|
1,33 |
Y Pb |
0,706 |
0,72 |
0,753 |
0,794 |
0,839 |
0,886 |
0,931 |
0,968 |
0,992 |
|
Y Ag |
0,996 |
0,98 |
0,95 |
0,903 |
0,84 |
0,764 |
0,678 |
0,589 |
0,505 |
Таблица 9
Рассчитанные значения T gas , yPb Pb-Ag сплава для « Т - х » диаграмм
|
P , Па |
х Pb |
0,01 |
0,03 |
0,05 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
|
133 |
Т gas , К |
2099 |
2034 |
1980 |
1916 |
1824 |
1766 |
1726 |
1694 |
1605 |
|
y Pb |
0,227 |
0,486 |
0,602 |
0,831 |
0,934 |
0,965 |
0,983 |
1,0 |
1,0 |
|
|
13,3 |
Т gas , К |
1799 |
1705 |
1666 |
1617 |
1543 |
1499 |
1468 |
1443 |
1423 |
|
y Pb |
0,375 |
0,56 |
0,685 |
0,92 |
0,967 |
0,984 |
0,994 |
0,996 |
0,997 |
|
|
1,33 |
Т gas , К |
1565 |
1480 |
1445 |
1399 |
1340 |
1305 |
1279 |
1259 |
1242 |
|
y Pb |
0,546 |
0,7 |
0,802 |
0,967 |
0,988 |
0,997 |
0,998 |
0,999 |
1,0 |
Таблица 10
Рассчитанные значения Р (Па) сплава Pb-Ag
|
Т , К |
x Pb |
||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
1073 |
0,007 |
0,016 |
0,027 |
0,04 |
0,056 |
0,074 |
0,093 |
0,113 |
0,132 |
|
1173 |
0,048 |
0,106 |
0,176 |
0,257 |
0,35 |
0,452 |
0,561 |
0,672 |
0,777 |
|
1273 |
0,246 |
0,526 |
0,850 |
1,218 |
1,624 |
2,065 |
2,527 |
2,986 |
3,431 |
|
1373 |
0,967 |
2,028 |
3,219 |
4,539 |
5,977 |
7,490 |
9,055 |
10,615 |
12,121 |
|
1473 |
3,146 |
6,456 |
10,091 |
14,053 |
18,243 |
22,675 |
27,156 |
31,59 |
35,917 |
|
1573 |
8,784 |
17,632 |
27,186 |
37,418 |
48,092 |
59,179 |
70,372 |
81,487 |
92,246 |
|
1673 |
21,686 |
42,565 |
64,753 |
88,207 |
112,39 |
137,24 |
162,21 |
186,77 |
210,91 |
|
1773 |
48,46 |
92,77 |
139,51 |
187,91 |
237,86 |
288,23 |
338,95 |
388,81 |
437,93 |
Таблица 11
Рассчитанные значения G1^ сплава Pb-Ag
|
T , К |
G m , Дж/моль |
||||||||
|
x Pb |
|||||||||
|
0,1 |
0,2 |
0 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
1073 |
– |
– |
10,233 |
64,36 |
135,31 |
211,75 |
275,22 |
296,32 |
228,82 |
|
1173 |
60,28 |
134,65 |
219,99 |
310,85 |
398,49 |
469,44 |
503,37 |
470,03 |
324,51 |
|
1273 |
133,07 |
267,23 |
398,01 |
518,48 |
618,4 |
682,85 |
690,53 |
611,1 |
401,44 |
|
1373 |
195,97 |
381,17 |
550,08 |
694,71 |
803,72 |
861,35 |
845,8 |
727,13 |
464,14 |
|
1473 |
250,55 |
479,54 |
680,69 |
845,19 |
961 |
1012 |
975,76 |
823,5 |
515,81 |
|
1573 |
298,05 |
564,79 |
793,34 |
974,33 |
1095 |
1139 |
1085 |
904,18 |
558,76 |
|
1673 |
339,55 |
638,99 |
890,99 |
1086 |
1211 |
1249 |
1178 |
972,3 |
594,78 |
|
1773 |
375,71 |
703,38 |
975,4 |
1182 |
1309 |
1341 |
1257 |
1030 |
624,88 |
|
- Н ^ , Дж/моль |
532,6 |
932,5 |
1371,1 |
1529,6 |
1532,4 |
1386 |
1106,8 |
731,41 |
323,15 |
|
5 Е ° m , Дж/моль·К |
0,5219 |
0,9405 |
1,3604 |
1,5735 |
1,6507 |
1,5859 |
1,3761 |
1,0265 |
0,5533 |
Заключение
Фазовые диаграммы для Pb–Ag сплавов различного состава при вакуумной перегонке рассчитаны на основе модели равновесия системы «жидкость – газ» ( VLE ), которая использует при расчете коэффициентов активности молекулярную модель объемного взаимодействия ( MIVM ). Существенное преимущество MIVM заключается в ее способности прогнозировать термодинамические свойства жидких сплавов, используя только коэффициенты активности для двоичных (бинарных) беско-
нечно разбавленных систем. Поэтому MIVM не использует эмпирические значения параметров, характеризующих потенциальную энергию парного взаимодействия. Для последующего практического использования важно оценить степень разделения и количественный состав продуктов с помощью фазовых диаграмм «температура – состав» ( Т–х ) и «давление – состав» ( Р–х ), что позволит выбрать условия обработки исходных материалов для получения продуктов заданного состава.
Список литературы Фазовые равновесия в системе Pb-Ag при пирометаллургической возгонке
- Berman A. Total Pressure Measurements in Vacuum Technology. New York, Academic Press Publ., 1985. 380 р.
- Winkler O., Bakish R. Vacuum metallurgy. Amsterdam, Elsevier Publ., 1971. 237 р.
- Jia G.-B., Yang B., Liu D.-C. Deeply Removing Lead from Pb-Sn Alloy with Vacuum Distillation. Transactions of Nonferrous Metals Society of China, 2013, vol. 23, no. 6, pp. 1822-1831 DOI: 10.1016/S1003-6326(13)62666-7
- Wang A., Li Y., Yang B., Xu B., Kong L., Liu D. Process Optimization for Vacuum Distillation of Sn-Sb Alloy by Response Surface Methodology. Vacuum, 2014, vol. 109, pp. 127-134 DOI: 10.1016/j.vacuum.2014.07.013
- Dai Y.N. Vacuum Metallurgy of Nonferrous Metals. Beijing, Metallurgical Industry Press Publ., 2009. 72 p.
- Yang B., Kong L.-X., Xu B.-Q., Liu D.-C., Dai Y.-N. Recycling of Metals from Waste Sn-Based Alloys by Vacuum Separation. Transactions of Nonferrous Metals Society of China, 2015, vol. 25, no. 4, pp. 1315-1324 DOI: 10.1016/S1003-6326(15)63730-X
- Liu D. C., Yang B., Wang F., Yu Q. C., Wang L., Dai Y. N. Research on the Removal of Impurities from Crude Nickel by Vacuum Distillation. Physics Procedia, 2012, vol. 32, pp. 363-371 DOI: 10.1016/j.phpro.2012.03.570
- Dai Y.N., Yang B. Non-Ferrous Metals and Vacuum Metallurgy. Beijing, Metallurgical Industry Press Publ., 2000. 40 p.
- Smith J. M., Van Ness H.C., Abbott M.M. Introduction to Chemical Engineering Thermodynamics. New York, McGraw-Hill Publ., 2001. 749 p.
- Tao D. P. A New Model of Thermodynamics of Liquid Mixtures and Its Application to Liquid Alloys. Thermochimica Acta, 2000, vol. 363, pp. 105-113 DOI: 10.1016/S0040-6031(00)00603-1
- Poizeau S., Kim H.J., Newhouse J.M., Spatocco B.L., Sadoway D.R. Determination and Modeling of the Thermodynamic Properties of Liquid Calcium-Antimony Alloys. Electrochimica Acta, 2012, vol. 76, pp. 8-15 DOI: 10.1016/j.electacta.2012.04.139
- Newhouse J. M., Poizeau S., Kim H., Spatocco B.L., Sadoway D.R. Thermodynamic Properties of Calcium-Magnesium Alloys Determined by EMF Measurements. Electrochimica Acta, 2013, vol. 91, pp. 293-301 DOI: 10.1016/j.electacta.2012.11.063
- Miyazaki N., Adachi N., Todaka Y., Miyazaki H., Nishino Y. Thermoelectric Property of Bulk CaMgSi Intermetallic Compound. Journal of Alloys and Compounds, 2017, vol. 691, pp. 914-918. DOI: 10.1016/j.jallcom.2016.08.227
- Materials Science and Technology. Cahn R.W., Haasen P., Kramer E. J. (Eds.). Vol. 1. Structure of Solids. Gerold V. (Ed.). VCH Weinheim Publ., 1993. 621 p.
- Hultgren R., Desai P. D., Hawkins D. T., Geiser M., Kelley K. K. Selected Values of the Thermodynamic Properties of Binary Alloys. ASM Publ., 1973. 847 р.
- Dai Y., Yang B. Vacuum Metallurgy for Non-Ferrous Metals and Materials. Beijing, Metallurgical Industry Press Publ., 2000. 124 р. (in Chinese).
- Yang H. W., Yang B., Xu B. Q., Liu D. C., Tao D. P. Application of Molecular Interaction Volume Model in Vacuum Distillation of Pb-Based Alloys. Vacuum, 2012, vol. 86, no. 9, pp. 1296-1299. 11.017 DOI: 10.1016/j.vacuum.2011
- Jiang W. L., Zhang C., Xu N., Yang B., Xu B. Q., Liu D. C., Yang H. W. Experimental Investigation and Modelling of Phase Equilibria for the Ag-Cu-Pb System in Vacuum Distillation. Fluid Phase Equilibria, 2016, vol. 417, pp. 19-24 DOI: 10.1016/j.fluid.2016.02.026
- Nan C. B., Xiong H., Xu B.-q., Yang B., Liu D. C., Yang H. W. Measurement and Modeling of Phase Equilibria for Sb-Sn and Bi-Sb-Sn Alloys in Vacuum Distillation. Fluid Phase Equilibria, 2017, vol. 442, pp. 62-67 DOI: 10.1016/j.fluid.2017.03.016
- Zhao J. Y, Yang H. W., Nan C. B., Yang B., Liu D. C., Xu B.-Q. Kinetics of Pb Evaporation from Pb-Sn Liquid Alloy in Vacuum Distillation. Vacuum, 2017, vol. 141, pp. 10-14 DOI: 10.1016/j.vacuum.2017.03.004
- Kong L.-X., Xu J., Xu B.-Q., Xu S., Yang B. Vapor-Liquid Phase Equilibria of Binary Tin-Antimony System in Vacuum Distillation: Experimental Investigation and Calculation. Fluid Phase Equilibria, 2016, vol. 415, pp. 176-183 DOI: 10.1016/j.fluid.2016.02.012
- Nan C. В., Yang H. W., Yang B., Liu D., Xiong H. Experimental and Modeling Vapor-Liquid Equilibria: Separation of Bi from Sn by Vacuum Distillation. Vacuum, 2017, vol. 135, pp. 109-114 DOI: 10.1016/j.vacuum.2016.10.035
- Song B., Xu N., Jiang W., Yang B., Chen X. Study on Azeotropic Point of Pb-Sb Alloys by Ab-initio Molecular Dynamic Simulation and Vacuum Distillation. Vacuum, 2016, vol. 125, pp. 209-214 DOI: 10.1016/j.vacuum.2016.01.004
- Zhang C., Jiang W. L., Yang B., Liu D. C., Xu B. Q., Yang H. W. Experimental Investigation and Calculation of Vapor-Liquid Equilibria for Cu-Pb Binary Alloy in Vacuum Distillation. Fluid Phase Equilibria, 2015, vol. 405, pp. 68-72 DOI: 10.1016/j.fluid.2015.07.043
- Kong L.-X., Yang B., Xu B.-Q., Li Y.-F., Li L. Application of Molecular Interaction Volume Model in Separation of Pb-Sn-Sb Ternary Alloy by Vacuum Distillation. Transactions of Nonferrous Metals Society of China, 2013, vol. 23, no. 8, pp. 2408-2415 DOI: 10.1016/S1003-6326(13)62748-X
- Dong Z. W., Xiong H., Deng Y., Yang B. Separation and Enrichment of PbS and Sb2S3 from Jamesonite by Vacuum Distillation. Vacuum, 2015, vol. 121, pp. 48-55 DOI: 10.1016/j.vacuum.2015.07.009
- Kong L. X., Yang B., Xu B. Q., Li Y. F. Application of MIVM for Pb-Sn-Sb Ternary System in Vacuum Distillation. Vacuum, 2014, vol. 101, pp. 324-327 DOI: 10.1016/j.vacuum.2013.10.004
- Kong L., Yang B., Xu B., Li Y., Liu D., Dai Y. Application of MIVM for Phase Equilibrium of Sn-Pb-Sb System in Vacuum Distillation. Fluid Phase Equilibria, 2014, vol. 364, pp. 1-5 DOI: 10.1016/j.fluid.2013.12.003
- Баранов М.А. Сферическая симметрия электронных оболочек атомов и стабильность кристаллов. Электронный физико-технический журнал. 2006. Т. 1. С. 34-48.


