Фазовый контроль при возбуждении квантового осциллятора экспоненциальным импульсом

Генерация электромагнитных импульсов с заданной абсолютной фазой (или СЕР -carrier envelope phase) открывает новые возможности фазового управления фотоиндуци-рованными процессами (фазовый контроль), в отличие от традиционного способа за счет изменения амплитуды поля [1]. Наряду с этим в последнее время достигнут значительный прогресс в технологии генерации коротких и ультракоротких импульсов с заданной длительностью (Нобелевская премия по физике за 2023 год, присужденная Ф. Краусу, А. Люийе и П. Агостини). Все это делает актуальным детализацию описания импульсного возбуждения вещества, при котором учитывается зависимость вероятности фотопроцесса от всех характеристик возбуждающего импульса.

Фазовый контроль возбуждения двухуровневой системы под действием гауссовского импульса анализировался в статье [2] с помощью численного решения уравнений Блоха. Было, в частности, показано, что с изменением абсолютной фазы можно практически свести к нулю населенность верхнего энергетического уровня после окончания действия импульса. Кроме того, были установлены границы применимости приближения вращающейся волны. В статье [3] теоретически исследовался фазовый контроль возбуждения классического осциллятора под действием ультракороткого лазерного импульса с переменной фазой и гауссовской огибающей. Рассматривался как гармонический осциллятор, так и осциллятор Морзе. В первом случае были получены аналитические выражения для коэффициента фазовой модуляции и спектральной функции возбуждения. В случае осциллятора Морзе численно рассчитывалась зависимость мощности излучения от абсолютной фазы для различных значений параметров импульса, а также энергия возбуждения как функция амплитуды одноциклового импульса.

Квантовый осциллятор является фундаментальной квантово-механической моделью, применимой для широкого круга материальных объектов. Уникальной чертой данной модели является возможность аналитического описания возбуждения при любой амплитуде внешнего воздействия [4,5]. Это позволяет учесть точно нелинейные эффекты электромагнитного взаимодействия и влияние на них параметров возбуждающего импульса. Так, в работе [6] аналитически и численно исследовалось возбуждение квантового осциллятора мультицикловыми электромагнитными импульсами с гауссовской огибающей и огибающей в форме гиперболического секанса для произвольного значения амплитуды поля. Были рассчитаны и проанализированы зависимости вероятности возбуждения от длительности, несущей частоты и амплитуды. Специфические черты возбуждения квантового осциллятора мультцикловыми импульсами с различными огибающими исследовались в статье [7]. Было установлено наличие двух режимов возбуждения: слабого и сильного, а также изучены зависимости вероятности возбуждения от параметров импульса для каждого из этих режимов. В работе [8] рассматривалось импульсное возбуждение классического гармонического осциллятора с затуханием для различных значений длительности, несущей частоты и формы огибающей импульса. Было, в частности, показано, что зависимость энергии возбуждения осциллятора имеет качественно различный характер в случае экспоненциального и гауссовского импульсов. Наконец, в недавней работе [9] исследовалось влияние абсолютной фазы на вероятность возбуждения квантового осциллятора из основного состояния под действием короткого электромагнитного импульса с гауссовской огибающей. Были рассчитаны и проанализированы временные и спектральные зависимости вероятности возбуждения для различных абсолютных фаз, а также установлен критерий возникновения фазовых эффектов для гауссовского возбуждающего импульса.

В данной статье аналитически и численно исследуется влияние абсолютной фазы экспоненциального импульса на вероятность возбуждения квантового осциллятора без затухания за все время действия импульса с произвольной длительностью и амплитудой.

В отличие от гауссовского импульса экспоненциальный импульс имеет резкий передний и экспоненциально затухающий задний фронт, что характерно для лазерных импульсов, генерируемых в режиме модуляции добротности. Для экспоненциального импульса можно получить относительно простое аналитическое описание возбуждения, при котором в явном виде прослеживается зависимость от параметров импульса, что позволяет установить качественные закономерности процесса.

2.    Основные формулы

Выражение для вероятности возбуждения квантового осциллятора из основного состояния в п-е стационарное состояние под действием электромагнитного импульса можно получить из общей формулы Швингера [4], оно имеет вид [6,9]:

Wо^_n(т,Шc,lp) =

п(т, Шс^У¹ п!

ехр(-п(т, шс,^))

где т, ш_с — длительность и несущая частота импульса, ^ — фаза «несущей по отношению к огибающей» (абсолютная фаза), п(т,ш_с,^) - среднее число квантов в результате возбуждения, которое для осциллятора без затухания равно

п(т,Шс,^)=^0^(шо,т,Шс,^)|2,                          (2)

здесь шо — собственная частота осциллятора,

И_о =   , ^qE 0

⁰  Д 2М бшо

— частота Раби, q, М — заряд и масса осциллятора, Ео — амплитуда напряженности электрического поля в импульсе, Е (шо ,т,ш_с,^) — фурье-образ нормированной на амплитуду напряженности электрического поля на собственной частоте осциллятора.

Заметим, что формулы (2) - (3) справедливы для импульса силы, пропорционального напряженности электрического поля:

F ^(t,т ) = q^{E (}t,^т ).

Равенство (4) отвечает прямому механизму возбуждения осциллятора, в отличие от непрямых механизмов, при которых сила пропорциональна второй степени поля.

Таким образом, согласно (1) - (2) вероятность возбуждения квантового осциллятора без затухания за все время действия импульса определяется квадратом модуля фурье-образа поля на собственной частоте осциллятора.

Нормированный на амплитуду напряженности электрического поля экспоненциальный импульс имеет вид

Е = 0(t) exp(—t/т) cos(ш_c t + ^).

d(t) — функция Хэвисайда, ^ — абсолютная фаза.

Квадрат модуля фурье-образа напряженности электрического поля экспоненциального импульса (5), который входит в выражение (2), определяя тем самым вероятность возбуждения квантового осциллятора (1), можно представить в виде

к

|Е_СХр(ш, Шс, т, ^)| = ^тСех_р(ш, Шс, т ) {1 + К_схр(ш, Шс , т ) cos(2^ + А^_схр)} ,       ( 6)

где х _ 2т         1 + (ш2 + ш2)т2

р^(ш, ^Шс, ^т ) = ^ [1 ₊ (ш + Шс)2т 2] [1 + (ш - Шс)2т2]

— спектральная форма импульса, для мультицикловых импульсов (ш_ст » 1) и околорезо-нансных частот ш = шо спектральная форма импульса (7) совпадает с лорецианом.

X    У^[1 + ^(ш + ^шс^{)2 т 2] [1} + ^{(ш - ш}с^{)2 т 2]}

л,,(ш,шс,т) =-------Г+щ+ЩЩ-------

— коэффициент фазовой модуляции,

А^Схр

= arccos

1 + (ш2 - ш2)т2

^[1 + (ш2 — ш2)т2]2 + 4ш2т2

— фазовый сдвиг. Заметим, что А^ехр(т = 0) = 0.

Собирая формулы (1) - (2) и (6) - (9) и полагая, что w = w q , получаем вероятность возбуждения квантового осциллятора из основного состояния в стационарное состояние п за все время действия импульса с учетом абсолютной фазы р.

Точные выражения (6) - (9) получены вне приближения вращающейся волны, в котором пренебрегается нерезонансными членами по сравнению с резонансными. Приближение вращающейся волны не применимо в данном случае, поскольку рассматриваются произвольные длительности, включая субцикловые импульсы.

Интересно сравнить фазовую зависимость возбуждения экспоненциальным импульсом с аналогичной зависимостью для возбуждения гауссовским импульсом

Ё = exp(-t²/2T ²)cos(w_ct + p),                           (10)

для которого

\Ё(ш, т, w_c, p)|² = ле^-(1Ё^+ш^^т2т ² ch(2ww_cT²) {1 + sech(2ww_cT²) cos(2p)} .

Отсюда следует, что коэффициент фазовой модуляции в случае возбуждения квантового осциллятора гауссовским импульсом (10) равен [9]:

K&(w,w_c ,т ) = sech(2ww_cT²).                            (11)

Это значение получается также для возбуждения классического осциллятора гауссовским импульсом [3].

Как видно из формулы (8), в пределе мультициклового экспоненциального импульса К_ехp(w_c = w q ,w _c t ^ 1) = 0. В этом же пределе коэффициент фазовой модуляции при возбуждении квантового осциллятора гауссовским импульсом равен нулю, как это следует из формулы (11). В этом состоит качественное различие фазового контроля под действием импульсов с различными огибающими.

3.    Результаты расчета

Сравнение коэффициентов фазовой модуляции при возбуждении квантового осциллятора экспоненциальным и гауссовским импульсом как функции длительности импульса приведено на рис. 1 для несущей частоты импульса w_c = 1.05 отн. ед. и собственной частоты осциллятора w q = 1 отн. ед.

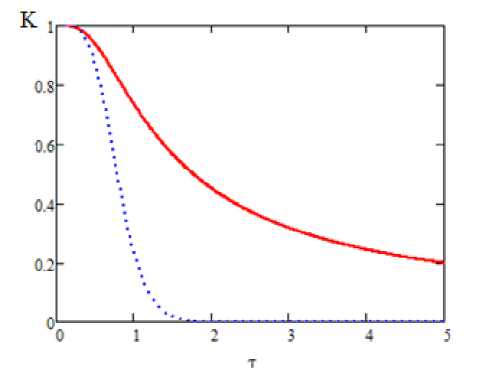
Рис. 1. Коэффициент фазовой модуляции как функция длительности импульса: сплошная кривая - экспоненциальный импульс, пунктир - гауссовский импульс; w₀ = 1, w_c = 1.05

В данной статье частоты и длительность импульса измеряются в относительных единицах, поскольку справедливо скэйлинговое преобразование w‘ ^ Sw т т' ^ т/S, где S - произвольная константа.

Из рис. 1 видно, что для субцикловых импулвсов ш_ст <  1 коэффициент фазовой модуляции близок к единице, а с ростом длительности импульса он уменьшается. При этом в случае гауссовского импульса уменьшение происходит существенно быстрее, чем для экспоненциального импульса (экспоненциальным образом, как это следует из формулы (И)).

На рис. 2 представлена зависимость коэффициента фазовой модуляции от длительности экспоненциального импульса для различных несущих частот. Видно, что в соответствии с (8) для околорезонансных несущих частот коэффициент фазовой модуляции убывает быстрее с ростом длительности импульса, однако к нулю он стремится только в случае точного резонанса ш = ш_с.

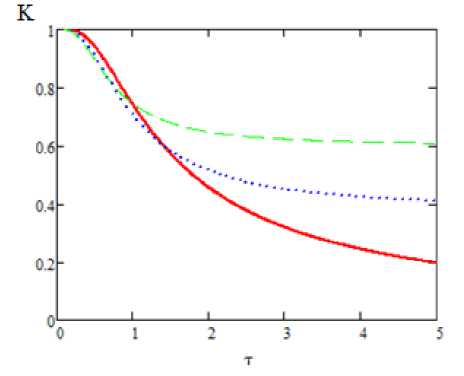
Рис. 2. Коэффициент фазовой модуляции как функция длительности экспоненциального импульса: сплошная кривая - ш_с = 1.01, пуиктир - ш_с = 1.5, штриховая кривая - ш_с = 2; шо = 1

Фазовый сдвиг (9) как функция длительности импульса показан на рис. 3 для различных несущих частот экспоненциального импульса. Видно, что для т = 0 сдвиг равен нулю, а с ростом частотной отстройки его асимптотическое значение (для больших длительностей) изменяется от т/2 до г, как это следует из формулы (9).

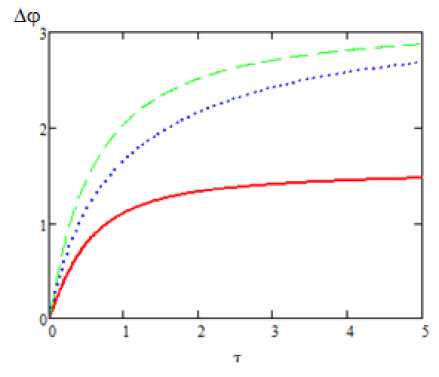
Рис. 3. Фазовый сдвиг А<р_ехр в зависимости от длительности экспоиеициальиого импульса: сплошная кривая - ш_с = 1, пуиктир - ш_с = 1.5, штриховая кривая - ш_с = 2; шо = 1

На рис. 4-5 показана зависимость от абсолютной фазы экспоненциального импульса вероятности возбуждения перехода 0-1 в квантовом осцилляторе для различных длительностей, а также для большего значения частоты Раби (рис. 5).

Видно, что с ростом параметра т глубина модуляции уменьшается (минимальное значение возрастает), а значение вероятности растет. При этом максимум фазовой зависимости незначительно смещается в область меньших значений абсолютной фазы.

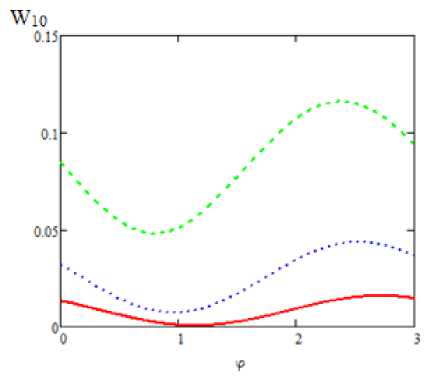
Рис. 4. Зависимость вероятности возбуждения перехода 0-1 в квантовом осцилляторе от абсолютной фазы экспоненциального импульса для различных длительностей импульса: сплошная кривая - т = 0.5, пуиктир - = =1, штриховая кривая - = = 2; ш_с = 1.1; шо = 1, И = 0.3

Для большого значения частоты Раби (рис. 5), отвечающего насыщению [7], уменьшение глубины фазовой модуляции становится более проявленным: вероятность возбуждения перехода 0-1 по мере роста абсолютной фазы осциллирует около своего среднего значения с малой амплитудой, а сдвиг максимума для = = 2 становится существенным.

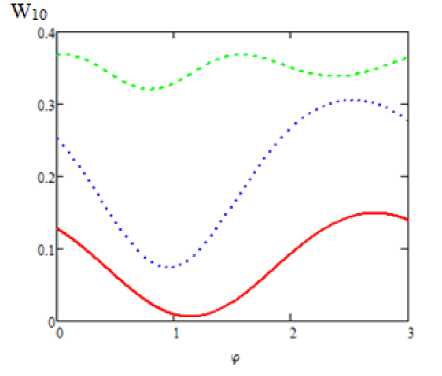
Рис. 5. То же, что на рис. 4 для большей частоты Раби Ио = 1

На рис. 6 представлена фазовая зависимость вероятности возбуждения перехода 0-1 для заданного значения длительности импульса и различных несущих частот.

Из рис. 6 следует, что увеличение частотной отстройки уменьшает величину вероятности и смещает ее максимум. При этом глубина фазовой модуляции изменяется несущественно.

Расчет показывает, что с увеличением частоты Раби и переходе в режим насыщения при больших частотных отстройках фазовая зависимость становится негармонической: максимум уширяется, приобретая столообразную форму, а глубина фазовой модуляции при этом увеличивается.

При возбуждении переходов 0- n с п >  1 качественные закономерности фазового контроля остаются прежними, отличаясь лишь по абсолютной величине.

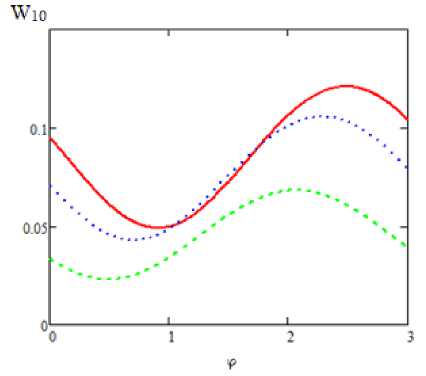
Рис. 6. Зависимость вероятности возбуждения перехода 0-1 в квантовом осцилляторе от абсолютной фазы экспоненциального импульса для различных несущих частот импульса: сплошная кривая - ш_с = 1, пуиктир - ш_с = 1.2, штриховая кривая - ш_с = 1.5; шо = 1, т = 2, Ио = 0.3

4.    Заключение

В работе установлены основные закономерности фазового контроля при возбуждении квантового осциллятора без затухания экспоненциальным импульсом. Получены аналитические выражения для коэффициента фазовой модуляции, фазового сдвига и спектральной формы импульса вне приближения вращающейся волны. Показано, что фазовый сдвиг в случае экспоненциального импульса, вообще говоря, не равен нулю в отличие от гауссовского импульса. Коэффициент фазовой модуляции максимален при малых длительностях импульса и увеличивается с ростом частотной отстройки несущей частоты от собственной частоты осциллятора для достаточно длинных импульсов. Фазовый сдвиг монотонно возрастает с ростом длительности импульса, асимптотически приближаясь к своему предельному значению, зависящему от вышеуказанной частотной отстройки.

Проведен численный расчет фазовой зависимости вероятности возбуждения перехода 0-1 в квантовом осцилляторе для различных длительностей и несущих частот экспоненциального импульса, а также для различных значений частоты Раби. Показано, что с ростом длительности импульса глубина фазовой модуляции уменьшается и максимум вероятности незначительно смещается в область меньших значений абсолютной фазы. Аналогичный сдвиг (но больший по величине) происходит с увеличением частотной отстройки несущей частоты импульса от собственной частоты осциллятора.

При переходе в режим насыщения с ростом частоты Раби фазовая зависимость вероятности становится более слабой, и положение фазовых максимумов существенно изменяется при изменении длительности импульса.

Работа выполнена при поддержке Министерства науки и высшего образования Российской Федерации в рамках государственного задания (договор 075-03-2023-106 от 13.01.2023).