Фазовый метод измерения параметров деформационного состояния лопастей несущего винта вертолета

Несущий винт - важнейший узел вертолета, от исправности которого зависит сохранность вертолета. Контроль состояния лопастей является актуальной проблемой, а её решение позволит существенно сократить риски крушения вертолета. В результате проведенного анализа существующих методов и систем контроля целостности лопастей вертолёта, был предложен и рассмотрен бесконтактный способ контроля целостности лопастей вертолёта [1-4]. Суть метода заключается в облучении гармоническим СВЧ сигналом объекта исследования, последующем приеме и обработке отраженного информационного потока излучения, модулирующим элементом для которого служат сами лопасти несущего винта.

Анализируя параметры отражённого от лопастей зондирующего СВЧ-сигнала, можно определить следующие характеристики несущего винта:

• •    целостность горизонтального шарнирного крепления лопасти за счёт измерения временных интервалов между временными отметками, полученными от соседних лопастей;

• •    целостность вертикального шарнирного крепления лопасти по амплитуде махового движения лопасти, пропорциональной разности фаз излученного и принятого отраженного сигналов;

• •    скручивание и угол установки лопасти посредством измерения длительности им пульсного сигнала, характеризующего отра- Жуков Семен Викторович, аспирант кафедры радиотехники. E-mail: zhukovsv91@inbox.ru

жённый от лопасти электромагнитный поток и сравнения его с информацией об угле установки лопасти, полученной от системы датчиков бортового регистратора параметров;

• •    низкочастотные изгибно-крутильные колебания посредством накопления и анализа измеренных амплитуд маховых колебаний и углов скручивания лопастей;

Измерительная система, реализованная на базе предлагаемого метода, также может выявлять несоконусность установки лопастей, сближение лопастей несущих винтов вертолета в соосной схеме (рис. 1) и распознавать такие явления как земной резонанс и флаттер.

Целью настоящей работы является изучение возможности измерения амплитуды махового колебания лопасти за счет использования одночастотного фазового метода с модуляцией несущей.

1. ФАЗОВЫЙ МЕТОД ОПРЕДЕЛЕНИЯ РАССТОЯНИЯ ДО КОНТРОЛИРУЕМОГО ОБЪЕКТА

Предложенный ранее амплитудный метод [1-4] определения амплитуды махового колебания лопасти имеет низкую точность вследствие малой помехозащищенности, поэтому для повышения точности измерений предлагается использовать одночастотный фазовый метод.

Фазовый метод измерения [5,6] амплитуды маховых колебаний основан на определении разности между фазовыми аргументами зондирующего излучения (опорного) и принятого отраженного (информационного) излучения от поверхности каждой лопасти. Структурная схема фазового измерителя амплитуды маховых колебаний представлена на рис. 2.

Работает измеритель амплитуды маховых колебаний следующим образом. Генератор масштабного сигнала формирует колебания с отно-

Рис. 1. Схема расположения приемо-передающего модуля на хвостовой балке вертолёта

сительно низкой частотой по сравнению с СВЧ несущей:

u_m = Acos(^t + ф₀), (1.1) где A , Ω и ϕ₀ – соответственно, амплитуда, частота и начальная фаза модулирующего масштабного сигнала.

Масштабный сигнал (1.1) в модуляторе изменяют амплитуду колебаний генератора СВЧ сигнала, в результате формируется модулированное по амплитуде зондирующее СВЧ излучение:

^иизл = ^ изл [1 + М cos(nt + ^ 0 )] cos^t + ф' 0 ), (1.2) где M – коэффициент амплитудной модуляции; ω ₀, ϕ ‘ ₀ и U _изл– частота, начальная фаза и амплитуда немодулированного несущего СВЧ сигнала, соответственно.

Посредством излучающей антенны модулированный зондирующий сигнал (1.2) направляется в сторону траектории движения контролируемых лопастей, частично сигнал отражается от лопастей несущего винта вертолёта и принимается приемной АФС:

цепях измерителя; t_r – время задержки сигнала при распространении его до лопасти и обратно; ω _д(t) – доплеровское приращение частоты; t_н , t_к – время начала и конца наблюдения; ϕ ‘ – приращение фазы несущего сигнала.

Доплеровское приращение частоты, с учетом рекомендаций [7], рассчитывается по формуле (1.4).

ffl(t) = - Т"^Ьг' cos(^(t)),    (1.4)

л0 + zm где ^(t) - угол между линией визирования и направлением вектора скорости v^ движущегося объекта контроля (лопасти), изменяющийся в соответствии с траекторией движения лопасти в зоне контроля; λ0 – длина волны несущего сигнала; λm – длина волны масштабного сигнала.

Сигнал, отраженный от лопасти и несущий в себе информационную составляющую в виде фазового набега, выделяется посредством синхронного детектора, состоящего из перемножи-теля и фильтра нижних частот (ФНЧ). Сигнал с выхода перемножителя формируется следующим образом:

SD = Упр cos(w0t + ф') cos(^0t + ф0) X tK toA(t)dt 11,

н

X 11 + Mcos f^⁽t - t r ⁾ + ф 0 + Ф отр + Ф изм + J_t

Для упрощения дальнейших преобразований, обозначим:

У = ^и пр |1 + Mcos I n(t - t_r⁾ + ф 0 + ф отр +

+ фотр + физм +

ftK ..... I Шд(t)dt

Г н

)|-

и_пр = ^_пр cos(^₀t + ф ' ) |1 + Mcos |^(t - t_r) +

+ ф0 + фотр + физм +

| wд(t)dt^|,

(1.3)

где U _пр– амплитуда принятого несущего сигнала; ϕ _отр – фазовый сдвиг, вызванный разностью хода зондирующего сигнала от лопасти до АФС; ϕ _изм – сдвиг фазы обусловленный задержкой в

В результате на выходе перемножителя: У г-                                    .

⁵О = 2 [cos(2^ 0 t + ф" + ф 0 ) + cos(ф")], где ϕ ‘‘ – приращение фазовой компоненты несущего сигнала без учета начальной фазы.

После выделения огибающей в ФНЧ получаем сигнал вида:

5фНЧ = cos(ф")-2рx

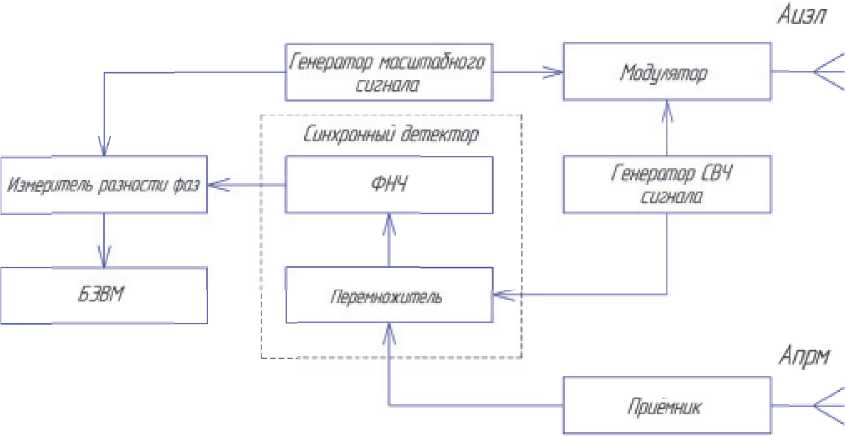
Рис. 2. Структурная схема измерителя амплитуды маховых колебаний

X

[1 + Mcos ^Q(t —

ty) + Фо +

+ ^фотр + ^ф изм

^ ^(t)dt)].

(1.5)

в преобразовании присутствуют еще и сдвиг фазы, обусловленный отражающими свойствами лопасти, задержкой фазы в цепях измерителя амплитуды маховых колебаний, а также компоненты доплеровской частоты. Вследствие

Далее сигнал (1.5) поступает на измеритель разности фаз, на второй вход которого в качестве опорного подается сигнал с генератора масштабного сигнала. В измерителе разности фаз сравниваются фазы (рис. 3) опорного и принятого масштабных сигналов. Результатом сравнения является прямоугольный импульс, длительность которого определяется величиной разности сравниваемых фаз.

В свою очередь фазовый набег Q t_r определяется расстоянием от лопасти до АФС и согласно [6, 8] может быть представлен выражением:

^ _ МП _ 4^Dfm _ 4^D

^{У c c} ^m’ .

того, что радиальная скорость вращения лопастей не превышает 250 м/с то для частот зонди-

рующего излучения равной (10…20) ГГц, оценка доплеровского приращения частоты по формуле (1.4) дает пренебрежимо малую величину. Фазовый сдвиг при отражении от облучаемого объекта определяется экспериментально и для

всех лопастей является одинаковым. Таким же

образом при калибровке устройства учитывается и запаздывание фазы в цепях измерителя амплитуды маховых колебаний [7-10].

При формировании выражения (1.7) не принимались во внимание фазовые сдвиги, связанные

с отражающими свойствами лопасти, задержкой фазы в цепях измерителя, а также доплеровским

где D – измеряемое расстояние; f_m – частота масштабного сигнала.

Таким образом, исходя из выражения (1.6), можно определить расстояние от АФС до лопасти:

приращением частоты. Эти неучтенные компоненты дают ошибку измерения дальности: ^^D   4л^ ^ ^фотр + ^физм + ^ Ш д ( ^t) d ^t ^.

^^ty C    ^.-^m^^ty

4nfm   4л

(1.7)

Длина волны масштабного сигнала определяется и задается исходя из максимально возможного измеряемого расстояния до контролируемой лопасти, в соответствии с выражением:

^ m = ^{2 D} max , где D _max – максимально возможное расстояние от лопасти до антенны, выбранное с учетом возможного махового колебания лопасти вертолёта.

Ошибки измерения дальности можно разделить на систематические и случайные. К систематическим относят ошибки измерения, вызываемые задержкой сигнала в цепях измерителя [11]. Систематические ошибки имеют постоянные зна-

чения, по крайней мере при использовании одних и тех же лопастей или в течение одного полёта, и могут быть скомпенсированы при калибровке

2. ПОГРЕШНОСТЬ ФАЗОВОГО МЕТОДА ИЗМЕРЕНИЯ АМПЛИТУДЫ МАХОВОГО КОЛЕБАНИЯ ЛОПАСТИ

Анализируя выражение (1.3) можно отметить, что помимо фазового сдвига, определяемого расстоянием до контролируемого объекта,

датчиков в процессе подготовки к полету.

Случайные ошибки вызываются неконтролируемыми причинами, имеют случайный характер и не могут быть полностью учтены. К случайным ошибкам измерений относят ошибки, связанные с помехами или нестабильностью частоты генератора [11]. Из-за неточности установки или нестабильности масштабной частоты может возникать ошибка измерения разности фаз ф_а [5,12]. Из выражения (1.6) следует, что ф_а и, соответственно, ошибка измерения амплитуды маховых колебаний D _а связаны соотношением:

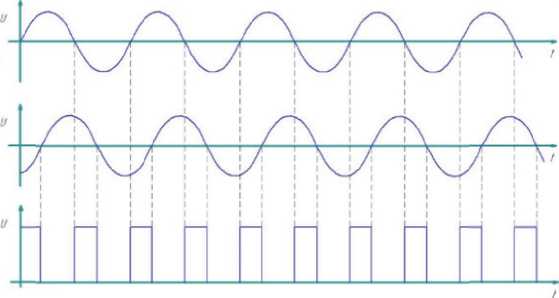
Рис. 3. Сравнение фаз излученного и принятого сигналов

D

a

С'фд 2Q

Ошибка определения разности фаз зависит от используемой радиоэлектронной элементной базы измерителя разности фаз и отношения сигнал/шум [12]. Если помеха представляет собой белый шум, а отношение q₀ - Р_с/Р_ш >> 1, где P с и P _ш мощности сигнала и шума соответственно, то средняя квадратическая ошибка разности фаз для идеального из -

мерителя определяется выражением:

1       1

Ф а

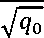
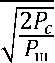
(2.1)

При увеличении мощности шумов, они начинают оказывать влияние на точность определения фазового сдвига и с уменьшением отношения q ₀, ошибка ϕ_σ увеличивается. Поэтому с учетом [11] и выражения (2.1) потенциальная среднеквадратическая ошибка измерения амплитуды махового колебания фазовым методом определяется:

_ Сфа _ С _ Ата - м;~ чщт.”

ЗАКЛЮЧЕНИЕ

Рассмотренный одночастотный фазовый метод измерения маховых колебаний лопастей, имеет более высокую точность по сравнению с амплитудным методом и относительно прост в реализации. Все возникающие ошибки могут быть сравнительно легко учтены и скомпенсированы. Предлагаемый метод может быть использован при работе со всеми типами вертолетов и установленных на них несущими винтами.