Феноменологическая модель гидродинамического кавитационного воздействия на водные системы

данном контексте способ получения кавитационных микропузырьков не имеет значения. Этим основным механизмам сопутствует повышение температуры и давления вблизи пузырька, делая локальную область около него уникальным реактором для проведения различных реакций и процессов. Предварительные результаты работы в этом направлении частично обобщены в монографиях [5-8]. В книге [5] рассмотрена краевая задача сопряжения для парогазового пузырька в жидкости, позволяющая путем детальных расчетов определить все особенности развития пузырька из зародыша и его схлопывания у твердой стенки. Там же на базе этой задачи рассмотрен частный случай для сферического пузырька в неподвижной жидкости. Результаты, полученные различными авторами, указывают на то, что при симметричном схлопывании пузырька создаются высокоинтенсивные поля давлений (до 5–10 тыс. атм.) и температур (до 15000 °С) [9–11].

Молекула H 2 O является самым легким и малым представителем химических и изоэлек-тронных гомологов. Ее свойства определяются максимально неоднородным распределением средней плотности электронов по молекуле, в результате чего на атомах молекулы H₂O сосредоточены наибольшие эффективные заряды [12, 13]. Уникальные свойства, парадоксы жидкой воды в большей степени объясняются наличием и развитостью водородных связей. В системе молекул H₂O водородная связь носит кооперативный характер, во многом определяя структуру воды при различных внешних условиях. Водородные связи примерно в 10 раз сильнее межмолекулярных взаимодействий, характерных для большинства других жидкостей.

В общем случае можно сказать, что взаимодействия большого количества молекул, ансамблей молекул, организация той или иной структуры, определяющей свойства воды, и соответственно, ее реакционную способность, обуславливаются коллективными силами Ван-дер-Ваальса. Приближенно закон соответственных состояний может быть выражен уравнением Ван-дер-Ваальса в виде

PV V a'N ------=---. NkT V - b VkT

Силы Ван-дер-Ваальса известны как дисперсионные, дальнодействующие. Они захватывают области >1000 A и определяют устойчивость той или иной структуры, физическую сорбцию и др.

Время релаксации для ряда процессов в воде при Т = 20 °С t = 10^-11-10^-13 с, а для некоторых - до t = 10^-1 4 с [9]. В связи с тем что продолжительность конечной стадии коллапса пузырька t = 10^-9-10^-8 с, становятся возможными процессы передачи энергии и перезарядки с участием молекул воды, благородных и активных газов, а также диссоциация молекул воды.

Таким образом, под действием гидродинамической кавитации как сильного воздействия происходит разложение (механолиз) воды [1]. Возбужденная молекула воды, наряду с излучением и диссипацией избыточной энергии в тепло, может диссоциировать:

H₂O ^∗ → H ⋅+ O ^& H ^∗ , O ^& H ^∗ → O ^& H + hυ .

За счет механолиза воды на H и OH в результате кавитационного воздействия происходит увеличение концентрации О при протекании в процессе механохимических реакций типа ⋅⋅

OH + OH → H₂O₂, ⋅

OH + H 2 O 2 → HO 2 + H 2 O,                                      (3)

^⋅

OH + HO₂ → H₂O + O₂ .

Одновременно изменяется структуры воды с образованием свободных водородных связей, что обуславливает ее повышенную активность и реагентную способность.

В случае водных систем активация, кроме механолиза воды, заключается в изменении степени равномерности распределения примесей по объему системы, агрегации и дезагрегации (диспергирования) примесей, а также в изменении их активного состояния. Важнейшей особенностью водных систем, в частности, является гетерогенность по примесям, которая в процессе кавитационного воздействия может существенно меняться. Под воздействием кавитации в водном растворе, содержащем инертные и активные газы, возможно существование разнообразных химических реакций [14–16].

Кавитационная обработка (в отличие, например, от омагничивания, воздействия различных полей электромагнитного происхождения и т.п.) дает устойчивые повторяющиеся результаты в получении модифицированной в процессе механолиза воды, воспроизводимые независимо от места и времени [1].

Наряду с указанными, в кавитационной полости протекают реакции трансформирования радикалов с участием химически активных газов и рекомбинации радикалов за время t = 10^- 7 - 10^-6 с. В результате этих процессов после коллапса кавитационного пузырька в раствор переходят продукты радикального разложения молекул H 2 O, обнаруженные с помощью метода спиновых ловушек [17], и рекомбинации радикалов, что приводит к накоплению в воде молекулярного O₂, H₂O₂, H₂ и других соединений. Высокая скорость протекания реакций свидетельствует о том, что они происходят непосредственно в зоне ^схлопывания пузырька.

Физическая модель кавитирующей жидкости

В гидродинамических процессах с развитой пузырьковой кавитацией, используемых в различных технологиях [1, 15, 16], наблюдаются сложнейшие пространственные интерференционные картины волн разрежения-сжатия как результат динамики коллапса кавитационных микропузырьков. Одновременно необходимо учитывать быстроменяющиеся поля высоких давлений и температур, а также турбулентные микропотоки, обуславливающие микроперемешивание среды. Анализ ранее полученных результатов свидетельствует о необходимости дальнейших более углубленных исследований с целью расширения сфер применения кавитационной технологии, уточнения исходных данных для расчета и проектирования суперкави-тирующих механизмов, уточнения физических и математических моделей процессов кавитационного воздействия на жидкие системы и твердые границы потоков. Здесь сделана попытка реализации новых подходов для решения реологических задач физики кавитации в области использования импульсных воздействий ее пузырьковых форм.

Свойства потоков при наличии кавитации значительно отличаются от свойств обычных потоков вследствие увеличения объема потока из-за бурного испарения жидкости с образованием кавитационных микропузырьков [5, 18]. Необходимо учитывать сжимаемость жидкости и усложненные уравнения состояния газа в пузырьках. Кавитация - явление, в котором участвуют несколько агрегатных состояний в развитом турбулентном режиме. В этом случае жидкость возможно рассматривать как своеобразную жидкую среду со структурой, образованной хаотически движущимися и взаимодействующими между собой и потоком молями. Следовательно, возникает необходимость более четкой интерпретации и учета в общем случае изменяющейся вязкости потока. Рассмотрев уравнения Навье-Стокса как запись второго закона Ньютона для моля жидкости, можно сказать, что скорость деформации должна учитывать возможную частоту актов молекулярного взаимодействия, вызванную гидродинамическим фактором относительного послойного смещения. Известно [19], что коэффициент динамической вязкости, учитывающий физико-химическую природу жидкости, должен учитывать размеры и массы молекул, их взаимное расположение, т.е. геометрический объем среды, приходящийся на «возбужденную» молекулу.

Задача сопряжения для пузырька в жидкости

Формы течений для пузырька в жидкости можно условно разделить на четыре типа: с образованием кумулятивной струйки; «холодное» кипение; газификация пограничного слоя; пульсация парогазового пузырька. В начальной стадии коллапса парогазового пузырька с образованием кумулятивной ультраструйки (по Корнфельду-Суворову, 1944) [20] необходимо учитывать гидро- и термодинамические процессы вне и внутри него. Для парогазовой (внутри пузырька , i = g ) и жидкой (вне пузырька, i = l ) сред можно записать исходные (базовые) уравнения физики (законы сохранения):

^+ V Л- ) р , ₊р м- 0;

Р, . t+(’r^)Vr    '; ■divП, р i

U + V-V)U = р^ + П. :$, О t где Пi - симметричный тензор напряжений; рi - массовая плотность; Vi - скорость; Fi - плотность газовых сил;

Р i q i = ^div ( ^ i grad T t¹ )

при передаче тепла лишь теплопроводностью по закону Фурье, U i – внутренняя энергия; S_i – тензор скоростей деформаций.

Замыкающими для системы (4)–(6) являются уравнения состояния:

калорическое:

рг=рг(^-, t" );

для воды по Тэту:

P + B P + B

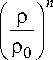
ⁿ i = ПК ,);

механическое для ньютоновских жидкостей:

П =-\ P i + -ц i div V^I + 2 ц i S i

I 3          )

На границе раздела фаз О ql высчитывают условия сопряжения по массе, скорости, импульсу энергии и температуре:

М lg = Р e j = Р ,

^gl

I™ „|

^p gjg ^p g

dQ„/ /- zX J ^ M^

I™ gl l

^,

где Z V = Z •¥„ ^g

– условие прилипания;

nП , ^+p l ^j V = ⁿⁿg ^+p g jV g

⁺ n a g l

1 )

V M    Ngi )

;

r   rv   ⁵ T

(n • П, V,-Xi —- + p, j 5 n

/

V

T + h , | = ⁽ n • П . V, + q . + p j

)

f V -

2 ⁺ h

^V

g

)

;

T = ^{T g +A T g}l .                                       0    0

При задании начальных и граничных условий на твердой стенке ( V , = 0), T , ⁰ = Т о⁰

полу-

чаем задачу сопряжения для системы сред «жидкость–газ». Частные случаи этих задач со сферической симметрией были получены Си-Дин-Ю (1965), Л.И. Седовым (1970), Р.И. Ниг матуллиным (1975-1978), В.М. Ивченко (1971-1977) [21, 22]. Для задач со сферической симметрией решение имеет хорошее совпадение с экспериментальной зависимостью радиуса R0 от времени τ [8]. Однако при рассмотрении данной задачи не все физические переменные были учтены (например, такие, как возрастание давления паров при R << Rmax, отклонение от сферичности вблизи стенок, влияние вязкости и др.). В этой связи имеем лишь качественно правильную картину.

Используя подход к рассмотрению турбулентных потоков, описанный в [23, 24], попы,          ,, таемся уточнить влияние вязкости в кавитационных течениях. Влияние вязкости сводится к демпфированию и связано с диссипацией механической энергии в процессе роста и схлопывания пузырьков. Такие расчеты в несжимаемой жидкости с учетом поверхностного натяжения были выполнены H. Poritsky [19] и обнаружили существенное влияние вязкости при значениях, заметно превышающих вязкость воды в обычных условиях. По методу [19] движение стенки пузырька описывают уравнением

P i

p ®

= RR + ³ R ² + 4 ^ ¹ R

р

2 р 2

Из формулы (17) можно получить уравнение энергии

( P - p.1R - R ) ' _R 3 _R 2 ₊ 32

t

4 ц [ RR ² dt = 0,

где последний член учитывает диссипацию энергии вследствие вязкости (на один стерадиан). Время схлопывания, определенное по (17), для пузырька без поверхностного натяжения становится бесконечно большим, если параметр

4^ ц = R0 .

превышает критическое значение, равное 0,46.

В работе Р.Д. Айвени [25] вязкость и поверхностное натяжение учитывали в сжимаемой жидкости. Был использован метод H. Poritsky, который F.R. Gilmore [26] применил в условиях сжимаемости, основываясь на гипотезе J.G. Kirkwood – H.A. Bethe [27]. Вязкость и поверхностное натяжение учитывали в граничном условии для давления в жидкости с помощью уравнения

Р = P i - — - 4 ц ¹ R. (20)

R 2

Согласно [25], вязкость и поверхностное натяжение не влияют на общий характер поведения каверны. Кажущиеся противоречия его результатов детально проанализированы в [2]. Результаты последующих работ, обобщенные в [5, 22, 28, 29 и др.], показывают, что вязкость, входящая в уравнение Навье-Стокса в виде коэффициента динамической вязкости, может быть учтена более или менее удачно. Однако физическая интерпретация этого коэффициента недостаточна [30].

Условимся, как это сделано в [30] на основании работ [31, 32], под частицами жидкости понимать молекулы, надмолекулярные образования, ассоциаты и более крупные образования как турбулентные вихри. Тогда и кавитационные микропузырьки и микровихри, образующиеся в результате их коллапса, можно ассоциировать с частицами жидкости. Исходя из этого, можно сформулировать следующую феноменологическую модель кавитирующей жидкости (в отсутствие твердых границ потока): кавитационный микропузырек в своей динамике движется в пространстве, структурированном микротурбулентными вихрями, образованными интерференцией волн разрежения-сжатия, возникающих в результате пульсации кавитационных микропузырьков.

Для изотропной среды (стохастически и статистически принимая поля кавитационных микропузырьков изотропной средой), физических констант, выражающих ее свойства, существует связь между тензором напряжений и скоростей деформации в виде соотношения [33]

П = aS + bl,

где a и b – скаляры. Скаляр a представляет собой физическую константу, которая из условия совпадения (21) со своим частным случаем, законом жидкостного трения Ньютона

—* dV

т = Ц-,~, dn

полагается равной 2 ц . Скаляр b может быть линейно связан с П и S через их линейные инварианты.

С помощью действий альтернирования и симметрирования уравнение движения в напряжениях возможно разбить на два, как это сделано в [30]:

vк(Пк^к 2Р^jj   5 -Vк(тД

V к ( ПХ -V к 2 рЫ j . „ + : .     ... j » к , „.

где V_d - скорость деформации движения; 5 rj - элементарный отрезок; to - угловая скорость.

Первое из этих уравнений характеризует движение сплошной среды в случае «симметричной» гидродинамики, а уравнение (24) – «несимметричной», когда в жидкости присутствуют непрерывно распределенные пары сил. Из уравнения (23) следует новое реологическое уравнение

П к - 2 ⁽Р V dk 5Л. V di 5_А ) - П.

или

ⁿ ki ^{- Р} V dk V di - Пи ^{- Р} S kj S ij ( 5 rj ) ^- n_k i .

Применительно к (25) вводится обозначение

M, - 1 Р V .5 r - 1 Р S_kj ( 5 r_} ) 2 . kj ₂ dk j ₂ kj j

Размерность тензора M kj совпадает с размерностью коэффициента динамической вязкости ц в (22). По физическому смыслу M_kj описывает внутренний момент импульса элемента жидкости, появляющийся вследствие его деформации при движении. Тогда

ⁿ ki ⁽ M k^{j S} i ^{j + M} k^{j S} k^j ) ^nl ki 2 ^M k^{j S j nl k}i .

В случае анизотропии переноса импульса и вещества с учетом (28) уравнение движения в напряжениях принимает вид

Р dV^ - -Р i F r i + 2 V r k ( M kj S & ij — H i l ki ) . dt

При задании тензора напряжений одним из выражений (25), (26) или (28) в уравне-нии Навье-Стокса (29) дополнительная вязкость как фактор регуляризации проявляется в любом сдвиговом течении (например, введение дополнительной вязкости необходимо для удержания детерминированности процесса, особенно в области больших скоростей

[34]).

Заключение

Таким образом, задача сопряжения для пузырька в жидкости может быть замкнута новым

реологическим уравнением или задана уравнением (29) с учетом тензора вязкости. Решение

для случая динамики сферического пузырька с учетом новой постановки задачи приводит к более точному совпадению с результатами эксперимента.

В итоге наряду с микротурбулентным перемешиванием и активацией поверхности водных полуфабрикатов процесс механолиза воды при ее гидромеханической обработке позволяет создавать и использовать кавитационную технологию для интенсификации различных технологических процессов и служит основой для разработки новых приложений [35–39 и др.].

Благодарность

Исследование выполнено при финансовой поддержке РФФИ и Правительства Красноярского края в рамках научных проектов № 18-48-242001 «Теплофизические и гидродинамические особенности кинетики смесеобразования при иммобилизации радиоактивных отходов в цементную матрицу с использованием эффектов кавитации», № 18-41-242004 «Теоретические основы кондиционирования вод питьевого назначения на базе эффектов гидродинамической кавитации».