Феррозондовые магнитометры с новым способом возбуждения на основе магнитоэлектрического взаимодействия

Взаимодействие человека с окружающей средой и, в частности, исследование земной поверхности на глубину до 10 м, так называемого подповерхностного пространства, связано прежде всего со строительством и эксплуатацией подземных инженерных коммуникаций, изучением условий распространения грунтовых вод и их минерализации, поиском археологических объектов и т. п. С каждым годом подобная приповерхностная природная геологическая среда интенсивно изменяется под действием различных промышленных сооружений (кабельных сетей, трубопроводов, теплотрасс, скрытых шахт и колодцев, подземных фундаментов, засыпанных рвов, канав, траншей), глубина залегания которых составляет от 1 до 5 м. Неконтролируемая динамика развития подобных процессов в конечном счете может привести к различным техногенным катастрофам, имеющим тя- желые социально-экономические последствия. Это в свою очередь вызывает необходимость проведения оперативного неразрушающего контроля состояния подповерхностного пространства в зоне активной инженерной деятельности [1–4].

В связи с этим возникает большое число геофизических задач, решение которых необходимо строить на неразрушающем дистанционном методе исследования, позволяющем легко и однозначно интерпретировать регистрируемую информацию об однородности исследуемых грунтов (вмещающей среды) и находящихся в них объектов.

В мировой практике для изучения структуры грунта и объектов, залегающих в верхней части подповерхностного пространства, используются различные методы геофизических исследований: электрическое и электромагнитное зондирование, магниторазведка, радиоволновое зондирование

(георадарометрия) и др. [5–11]. Каждый из них наряду с преимуществами обладает определенными недостатками: большие временные затраты, необходимость гальванического контакта с грунтом (методы постоянного тока), недостаточная информативность данных, низкая помехоустойчивость (частотное картирование, магниторазведка), узкая область применения (трассоискатели), сложность интерпретации и высокая стоимость аппаратуры (георадары).

В настоящее время интенсивно развиваются и получили соответствующее практическое применение методы геофизических исследований, основанные на магнитометрических измерениях, которые используются широким кругом научных и производственных организаций при решении специализированных задач: трассирование кабельных линий и трубопроводов, поиски затонувших судов, подземных неразорвавшихся мин и снарядов, изучение поведения оползней, обнаружение и изучение объектов археологических изысканий и т. д. [12–18]. Все эти задачи объединяются общей проблемой, которая связана с изучением магнитных аномалий, обусловленных магнитными источниками, лежащими на небольшой глубине, не превышающей 10 м, и создающими различные магнитные аномалии от 1 нТл до нескольких тысяч нТл на фоне существующих магнитных характеристик вмещающей среды. Например, подземные трубопроводы создают интенсивные аномалии от 100 до 1000 нТл, которые хорошо проявляются в магнитных полях. Причем износ металла трубопроводов, связанный с процессом коррозии (например, появление ржавчины), вызывает уменьшение магнитной восприимчивости. В магнитном поле эта химическая реакция может отметиться четкой отрицательной локальной аномалией. При этом аномалии могут иметь положительные и отрицательные части, а их форма в плане будет отражать конфигурацию самого объекта.

Рассматриваемые задачи эффективно решаются техническими средствами из арсенала малоглубинной магниторазведки, представляющей со- бой самостоятельное научно-практическое направление разведочной геофизики, занимающееся изучением и выделением намагниченных источников приповерхностной части земной коры, окруженных естественным магнитным полем. Кроме того, малоглубинная магниторазведка широко используется для поиска местоположения различных подземных коммуникаций.

Среди этих технических средств, ориентированных на определение параметров магнитных полей, наибольшее распространение получили феррозондовые магнитометры, которые осуществляют измерение физических величин, используя в качестве рабочей среды фоновое геомагнитное поле [19–25].

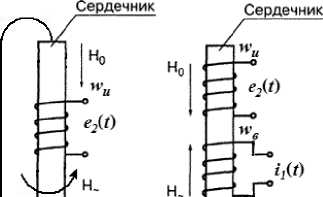
Феррозондовые магнитометры (феррозонды) характеризуются не только достаточно высокой чувствительностью, но и возможностью непосредственного измерения составляющих вектора магнитного поля, обеспечивая тем самым получение полной информации о структуре поля и его источниках. Они могут работать в очень слабых магнитных полях, в широком температурном диапазоне и при наличии электромагнитных помех, отличаются высокой надежностью, долговечностью и низкой стоимостью. Существуют несколько основных конструктивных типов феррозондов: стержневые одноэлементные и дифференциальные с разомкнутым или замкнутым кольцевым сердечником (рис. 1).

Известно, что для любого из указанных типов феррозонда свойственна двухмодульная функциональная структура: 1 – модуль модулятора, состоящий из структурированной ферромагнитной системы (сердечник) и излучающего (возбуждающего) элемента в виде катушки возбуждения w в ; 2 – модуль регистратора в виде приемной (измерительной) катушки индуктивности w и . В феррозондах внешнее измеряемое поле напряженности H 0 непосредственно воздействует на ферромагнитные сердечники модулятора. На эти же сердечники действует и переменное поле H ∼ , создаваемое током i ₁(t) катушки возбуждения w _в модулятора.

iAh

Одноэлементные стержневые феррозонды

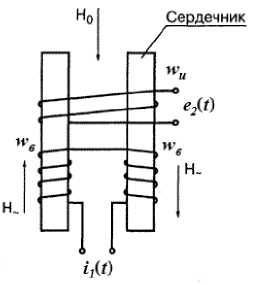
Дифференциальный феррозонд с разомкнутым сердечником

Рис. 1. Основные типы феррозондов

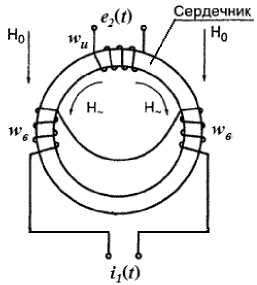
Дифференциальный феррозонд с замкнутым сердечником

Преобразование напряженностей H ₀ и H _∼ в переменную магнитную индукцию B ( t ) = B [ H _∼ , H ₀], а затем в e 2 ( t ) = e 2 [ B ( t )], появляющуюся в измерительной катушке w и , осуществляется так же, как и в магнитном усилителе.

В обширной литературе, посвященной анализу работы магнитных модуляторов и феррозондов, рассмотрены разнообразные режимы возбуждения этих устройств: заданное напряжение прямоугольной и синусоидальной формы, заданный ток синусоидальной, треугольной, трапецеидальной, ступенчато-прямоугольной формы и др. Варианты практического построения цепи возбуждения выбираются, как правило, исходя из соображений уменьшения затрат мощности на возбуждение и возможности обеспечения оптимального режима. Для всех указанных типов феррозондов в модуляторе в качестве возбуждающего фактора используется переменное магнитное поле, создаваемое током катушки возбуждения. В этом случае возбуждаемый в сердечниках модулятора магнитный поток вызывает соответствующие осцилляции их намагниченности.

Анализ особенностей функционирования известных типов феррозондов показал, что конструктивные и технологические методы повышения их эксплуатационных характеристик в рамках традиционных подходов и решений в основном себя исчерпали. Одно из возможных эффективных решений данной проблемы лежит в сфере разработки феррозондов, в основу работы которых заложена реализация физических явлений, ранее не использующихся в феррозондах, приводящая к качественному скачку в улучшении их выходных показателей.

Проведенные исследования и анализ физических процессов, реализуемых при работе модуляторов феррозондов, показали, что одним из перспективных направлений нетрадиционных путей улучшения их технико-экономических показателей является применение нового физического принципа возбуждения модулятора. В основе этого принципа лежит магнитоэлектрический эффект, инициируемый в сердечнике модулятора феррозонда переменным электрическим полем при его воздействии на локальную магнитоупорядоченную неоднородность, искусственно созданную в этом сердечнике. Для более полного представления сути предлагаемого способа возбуждения феррозондов рассмотрим особенности физических эффектов, на которых он основывается, на примере ферромагнитной системы модулятора феррозонда, состоящей из неметаллических ферромагнетиков, т. е. ферритов.

Принято считать, что ферритовые элементы обладают поликристаллическими доменными структурами, представляющими собой скоррелли-рованные системы, в которых ориентация магнитных моментов доменов одного кристалла воздей- ствует на ориентацию магнитных моментов доменов соседних кристаллов, превращая весь объем образца в самоорганизующуюся систему. Кроме того, если ферритовые элементы обладают локальной неоднородностью в виде магнитоупорядоченной структуры, то при определенных условиях в этих локальных неоднородностях могут возникать магнитоупругие взаимодействия, в которых переменными величинами будут являться как компоненты напряжения (или деформации), так и компоненты намагниченности. Иными словами, при наличии подобной магнитоупругой связи упругие колебания в локальной неоднородности будут вызывать соответствующие колебания векторов MS доменов и доменных границ, фактически являющихся областями, в которых вектор намагниченности плавно разворачивается при переходе от одного домена к другому. В этом процессе доменные границы, по сути, будут представлять собой магнитные спирали-солитоны, что в итоге и предопределит наличие некоторой ассоциированной электрической поляризации этих доменных границ, а значит, и соответствующую возможность управления ими с помощью электрического поля. В этом случае доменные стенки выступают в роли пьезоэлектрических структурных компонент, а сами домены можно считать магнитострикционными структурными компонентами. При этом внутри каждого домена подобной многодоменной структуры существует анизотропная магнитострикционная деформация, т. е. спонтанная магнитострикция.

Обобщая, можно констатировать, что воздействие электрического поля на подобные скоррелированные системы в структуре локальной неоднородности может привести к соответствующим изменениям модулей упругости, диэлектрической и магнитной проницаемости, а также пьезоэлектрических и магнитоупругих модулей этой локальной неоднородности с магнитоуопорядоченной структурой, которая в итоге может выступать в качестве источника магнитоэлектрических взаимодействий.

Следует отметить, что сами ферриты как композиционные материалы по своим свойствам относятся в определенном смысле к магнитоэлектрическим материалам, основным эффектом в которых является магнитоэлектрический эффект (МЭЭ), заключающийся в индуцировании электрической поляризации в материале во внешнем магнитном поле или в появлении намагниченности во внешнем электрическом поле. Иными словами, особенность МЭЭ заключается в том, что он связывает полярный вектор (поляризация) с аксиальным вектором (напряженность магнитного поля) и, наоборот, аксиальный вектор (намагниченность) с полярным вектором (напряженность электрического поля), вследствие чего МЭЭ можно отнести к перекрестным эффектам. Причем для рассматриваемого случая, т. е. для магнитоупорядоченной структуры ферритового элемента, МЭЭ возникает на неоднородностях типа доменных границ.

Исходя из этого, следует, что существует реальная возможность инициировать в ферритовых элементах возникновение МЭЭ, который относится к перекрестным эффектам и обусловлен механическим взаимодействием электрической, магнитной и упругой подсистем этих ферритовых элементов. При этом на частоте электромеханического резонанса возможно увеличение МЭЭ, а его дальнейшее усиление может иметь место при совпадении электромеханического и магнитного резонансов.

Таким образом, возникновение МЭЭ в ферритовом элементе связано прежде всего с механическим взаимодействием их магнитострикционной (пьезомагнитной) и пьезоэлектрической подсистем и заключается в возникновении поляризации вещества под действием магнитного поля (прямой МЭЭ) и в возникновении намагниченности вещества под действием электрического поля (обратный МЭЭ):

Pi =ayHj; M a E где Pi – электрическая поляризация; Mi – намагниченность; Hj – магнитное поле; Ej – электрическое поле; αij = αji – магнитоэлектрическая восприимчивость.

В этом случае, для материала, помещенного в однородные магнитное и электрическое поля, изменение объемной плотности свободной энергии может быть представлено следующим образом:

dF = - P i • dE j - M i • dH j .

Подобный перенос энергии магнитоэлектрического возбуждения в твердых телах составляет одну из наиболее фундаментальных проблем современной физики конденсированного состояния. Проблема эта весьма универсальна, поскольку перенос энергии магнитоэлектрического возбуждения является промежуточным процессом, который осуществляется между первичным актом возбуждения магнитоэлектрического процесса и теми конечными процессами, в которых эта энергия используется. Исходя из этого, можно элементарный акт «индуктивно-резонансного» переноса энергии рассматривать, как результат перекрестного взаимодействия двух элементарных разнородных подсистем (элементарных ячеек) – донора и акцептора энергии. В этом случае можно считать, что вся структура материала фактически состоит из таких элементарных ячеек, образованных соответствующими элементарными подсистемами. Если структура подобного материала композита возбуждена каким-либо образом, то возбуждение может быть локализовано в любой из этих элементарных ячеек. Следует отметить, что такое локализованное возбуждение не отвечает стационарному состоянию. Поэтому существующая связь между элементарными подсистемами и резонанс, обу- словленный идентичностью соответствующих элементарных ячеек, приведут к тому, что энергия возбуждения будет мигрировать от одной ячейки к другой, образуя эволюционирующую, самоорганизующуюся систему.

Так как подсистемы в композитной структуре механически связаны, то в пьезомагнитной подсистеме возникнут соответственно уже магнитоупругие деформации, порождающие, в свою очередь, намагниченность данной подсистемы, которая вызывает механические напряжения в пьезоэлектрической подсистеме, что приводит уже к ее электрической поляризации, т. е. к возникновению внутреннего электрического поля. Подобная взаимообусловленность двух эффектов (обратного и прямого МЭЭ) порождает непрерывный процесс их пространственно-временного взаимодействия, который в условиях совпадения электромеханического и магнитного резонансов приведет к существенному усилению индукции переменной намагниченности, а значит, и к повышению чувствительности феррозондового магнитометра.

Исходя из рассмотренных особенностей процесса возникновения МЭЭ, можно констатировать, что под воздействием источника магнитоэлектрических взаимодействий в виде локальной неоднородности структуры ферритового элемента возможно инициирование соответствующих изменений магнитных свойств объемных магнитострикционно-пьезоэлектрических структур самого ферритового элемента, т. е. возможна реализация эволюционирующего процесса пространственной модуляции намагниченности. Иными словами, воздействие подобного источника магнитоэлектрических взаимодействий приведет к изменениям распределения намагниченности, а сама величина этого эффекта будет достигать наибольшего значения в области максимальной неоднородности намагниченности.

Таким образом, можно утверждать, что воздействие переменным поперечным электрическим полем E _~ на локальную неоднородность в виде магнитоупорядоченной структуры с продольной намагниченностью M 0 = х • H = , находящейся в центре стержневой ферромагнитный системы, приводит к возбуждению в данной структуре МЭЭ. В свою очередь, наличие подобного МЭЭ способствует переводу указанной магнитоупорядоченной структуры в состояние непрерывной генерации магнитоэлектрического взаимодействия, которое уже инициирует соответствующий эволюционирующий МЭЭ во всей однородной структуре ферромагнитной системы. При этом продольная намагниченность M 0 = х • H = локальной неоднородности дополнительно обеспечивает максимальное значение магнитной проницаемости материала всей ферромагнитный системы, интенсифицируя все ее эндогенные физические процессы.

Исходя из особенностей функциональной структуры феррозонда и режимов его работы, а также специфики процессов возникновения МЭЭ в магнитоупорядоченных структурах ферримагнетиков, можно предложить новый способ его возбуждения (рис. 2), который осуществляется следующим образом.

В центре ферромагнитной системы 1 модулятора феррозонда, в качестве материала которой выбран феррит, создают локальную неоднородность в виде магнитоупорядоченной структуры путем добавления в ферромагнитную систему 1 постоянного магнита (ПМ) 2 из композита с намагниченностью вдоль оси ферромагнитной системы, который выбирают таким образом, чтобы создаваемая им напряженность магнитного поля обеспечивала максимальную магнитную проницаемость материала ферромагнитной системы 1 модулятора. Затем воздействуют внешним переменным электрическим полем на магнитоупорядоченную структуру ПМ 2 перпендикулярно его продольной оси. После чего на совпадающих частотах электромеханического и магнитного резонансов создают в магнитоупорядоченной структуре ПМ 2 режим генерации МЭ взаимодействий, посредством которых возбуждают в волноводных элементах ферромагнитной системы 1 стоячую магнитоэлектрическую волну 3 таким образом, чтобы для работы феррозонда в режима градиен-томера на всей длине ферромагнитной системы укладывалось 3/2 длины λ стоячей магнитоэлектрической волны с расположением ее средней пучности 4 по геометрическому центру ферромагнитной системы 1, а для функционирования феррозонда в режиме полемера на всей длине ферромагнитной системы 1 укладывалась одна длина λ стоячей магнитоэлектрической волны 3 с расположением ее среднего узла 5 по геометрическому центру ферромагнитной системы 1 (см. рис. 2).

Устройство модулятора для возбуждения феррозондов показано на рис. 3.

Модулятор состоит из ферромагнитной системы 1, содержащей два ферромагнитных стержневых полуэлемента конечной длины 1 ′ и 1 ″ , соосно состыкованных между собой коротким стержневым ПМ 2 с намагниченностью вдоль оси стержней; электродов 6 и 7, расположенных между внешней 8 и внутренней 9 диэлектрических цилиндрических втулок и охватывающих часть длины центральной части ферромагнитной системы 1, и заземленный электрод 10 в виде боковой поверхности разрезного тонкостенного металлического цилиндра, расположенного снаружи внешней втулки 8. Совокупность элементов 6–10 образуют вариант излучающей С-антенны. В составе феррозонда периферийный конец полуэлемента 1 ′ модулятора размещен внутри приемной катушки 11 ′ , а периферийный конец полуэлемента 1 ″ размещен внутри приемной катушки 11 ″ .

Описанный модулятор, реализующий предложенный способ возбуждения феррозондов, работает следующим образом (см. рис. 2 и рис. 3). ПМ 2 создает в ферромагнитных полуэлементах 1 ′ и 1 ″ ферромагнитной системы 1 подмагничиваю-

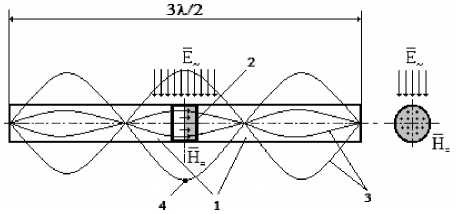
В режиме градиентомера

Рис. 2. возбуждение феррозонда в различных режимах работы

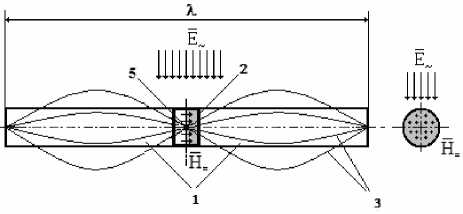
В режиме полемера

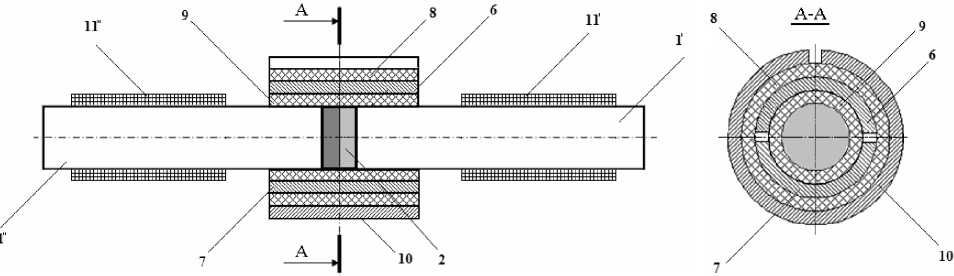
Рис. 3. Устройство модулятора для реализации нового способа возбуждения феррозонда

щее продольное постоянное магнитное поле напряженностью H ПМ , обеспечивающее максимальную величину начальной магнитной проницаемости µ = F ( H _ПМ) материала ФС 1:

lim µ = max µ = µ ^*.                    (1)

H _ПМ → Н    H

При подаче напряжения высокой частоты u _Г ( t ) = U_m ⋅ cos ω t на электроды излучающей С-антенны в магнитоупорядоченной структуре материала ПМ создается поперечное переменное электрическое поле (ПЭП):

_E ( _t ) =β⋅ ϕ 1 ( t ) -ϕ 2 ( t ) = δ

= β⋅ u _Г( t ) δ = E_m ⋅ cos ω t ,                    (2)

β где E = U ⋅   – амплитудное значение напря- m mδ женности электрического поля; β – конструктивный коэффициент С-антенны; δ – средний зазор между электродами С-антенны.

При этом заземленный электрод 10 излучающей С-антенны выполняет функции электростати- ческого и электромагнитного экранов, что существенно уменьшает влияние различных физических факторов на устойчивость рабочего режима феррозонда в целом. Кроме того, особенности конструктивного исполнения электрода 10 обеспечивают необходимые уровни локализации и интенсивности ПЭП, что значительно повышает эффективность работы устройства модулятора.

Поперечное ПЭП, взаимодействуя с продольно-магнитоупорядоченной структурой ПМ 2, пе- реводит данную структуру в состояние режима генерации магнитоэлектрических колебаний, которые в свою очередь через контактные поверхности в структурах ферромагнитных полуэлементов 1′ и 1″ на совпадающих частотах электромеханического и магнитного резонансов возбуждают эволюционирующий неоднородный МЭЭ в виде соответствующего потока магнитоэлектрической индукции ФМЭ, описываемый с учетом (2) волновым уравнением d2Φ МЭ = 2 dt2

⋅

d ² Φ _МЭ d ² x ,

где Ф МЭ – описывает некоторое свойство волноводов, связанное с волной; с ² – константа, характеризующая свойства среды (например, скорость распространения волны в среде).

Общее решение уравнения (3) можно записать в виде

Ф _МЭ ( x , t ) = f ( x – c ⋅ t ) + g ( x + c ⋅ t ), где f и g – произвольные функции.

Конкретизируем функции f и g следующими выражениями:

f ( x – c ⋅ t ) = a ⋅ sin( k ⋅ x – ω⋅ t ) ;

g(x+c⋅t) = a ⋅sin(k⋅x+ω⋅t), где с = ω/k – волновая скорость, k = 2π/λ – волно- вой коэффициент, λ – длина волны; а – амплитудное значение потока МЭ индукции.

В этом случае получим решение уравнения (3) в виде стоячей волны:

Ф_МЭ ( x , t ) = 2 ⋅ a ⋅ cos ω ₀ t ⋅ sin kx =

= 2 ⋅ Ф _m ⋅ cos ω ₀ t ⋅ sin kx , (4) где ω = ω ₀ – циклическая частота стоячей магнитоэлектрической волны на совпадающих частотах электромеханического и магнитного резонансов; а = γ · α · Е_m = Ф _m , где γ – коэффициент эволюции магнитоэлектрической волны, α = dP / dH – коэффициент магнитоэлектрической восприимчивости, dP и dH – соответственно изменения поляризации и приращения магнитного поля.

Точки x = n · π / k , в которых все время Ф_МЭ = 0, являются узлами волны, а точки x = (2 n + 1)· π /2 k , в которых Ф_МЭ достигает максимальных значений, образуют пучности волны. При х = λ 0 /4 для выражения (4) можем записать

Φ _МЭ = 2 ⋅ a ⋅ cos ω ₀ t = 2 ⋅Φ _m ⋅ cos ω ₀ t . (5)

Фактически данный волновой процесс можно рассматривать как пространственно-временную эволюцию некоторого состояния материала ферромагнитных полуэлементов 1 ′ и 1 ″ , инициирующий возникновение периодичной магнитной модуляционной структуры (ММС) с периодом Т = 2 π / ω 0 и с распределенной вдоль продольной оси ферромагнитной системы осциллирующей магнитной проницаемостью:

2 π x

µ=η⋅γ⋅ E ( t ) = 2 ⋅η⋅γ⋅ E_m ⋅ cos ω ₀ t ⋅ sin , (6) λ ₀

где η – коэффициент преобразования энергии электрического поля в энергию магнитоэлектрической волны; β – коэффициент инверсного магнитоэлектрического преобразования; x – координата вдоль распространения волны.

При этом сами ферромагнитные стержневые полуэлементы 1 ′ и 1 ″ выполняют функцию магнитоэлектрических волноводов, канализирующих эволюционирующий процесс магнитоэлектрического взаимодействия.

С учетом того, что рассматриваемый резонансный режим предполагает расположение пучности магнитоэлектрической волны на координате х = λ 0 /4, выражение (6) можно представить в виде

Ц = 2 -ц m - cos ® 0 t = Ц Р ( t ), (7) где µ m = η · β · E m – амплитудное значение магнитной проницаемости ФС.

Фактически образующаяся в ФС стоячая магнитоэлектрическая волна «навязывает» магнитной системе ФС ММС c соответствующим периодом Т .

Наличие подобной ММС, возникающей за счет движения и трансформации доменных границ в структуре ФС, приводит к периодическому изменению в каждом из них соответствующей средней намагниченности:

^M = У/\ j^Mj,

где nj = Vj / ^, Vj и Mj — соответственно относитель-j ный объем и намагниченность j-й группы доменов.

При наличии медленно изменяющегося измеряемого магнитного поля H 0 (t) выражение для намагниченности М можем записать

M = M = x ■ H o ( t ) =

(. ,*-,,_        ^

' ■Ц- 1 ■ H ( t ), (9)

l Ц 0         J

*

где X =

Ц

-

Ц о

V

Ц о

■Ц- 1

– магнитная восприимчивость.

Из выражения (9) следует, что измеряемое постоянное магнитное поле H 0 (t), направленное вдоль продольных осей симметрии ферромагнитных волноводов, трансформируется в стоячую волну магнитного поля за счет параметрической модуляции осциллирующей магнитной проницаемости материала ферромагнитного волновода.

Если периферийную часть первого ферромагнитного стержневого полуэлемента 1 ' модулятора поместить внутрь приемной катушки 11 ' (см. рис. 3), то на нее будут воздействовать поток магнитоэлектрической индукции Ф_МЭ и осциллирующая составляющая измеряемого магнитного поля, полученная в результате модуляции этого поля волной индукции переменной намагниченности. В результате этих воздействий в приемной катушке соответственно возникнут магнитоэлектрическая э.д.с. ( e МЭ ), пропорциональная d Ф МЭ / dt и магнитомодуляционная э.д.с. ( e _ММ), пропорциональная dM / dt.

Исходя из вышесказанного и с учетом (5), можем записать выражения для магнитоэлектрической э.д.с.:

e M Э = ⁹ ^ ^ МЭ = ^{8 5} ■ w ^-Ю 0 ^-Ф m • sin ® 0 t = dt

= K M3 ^-® 0 ^-Ф m ■ ^sin ® 0 t ,

где 9 = - 4- л - w • 5 - соответствующая константа связи;

w и s – соответственно количество витков катушки и площадь сечения ФС; K _Мэ = 8 ■ п ■ 5 ■ w - коэффици-

ент магнитоэлектрического преобразования.

Аналогично можем представить выражение и для магнитомодуляционной э.д.с:

^e MM

dM dt

= 9"

*

Ц "Ц е 1л ^dH0  ,, d Ц|   ^dH 0

--<Ц---+ H 0 ( t ) >

Ц 0      [ dt            dt J     dt

а Ц * "Ц 0 тт ^{d Ц}

= ⁹ ■          ■ H 0 ■     =

Ц ₀ dt

*

e            и Ц "Цо      ■

= 8 ■ П ■ 5 ■ w ■to o ■ H ₀--- Ц _m • sin to ₀ 1 =

Ц 0

= K MM -® 0 ■ ^H 0 ■Ц m ■ ^sin ® 0 t ,

* Ц -Ц_о где K _ММ = 8 ■ п ■ 5 ■ w ---коэффициент магни-

Ц 0

томодуляционного преобразования.

Если периферийную часть второго стержневого полуэлемента 1 " ферромагнитной системы поместить внутрь другой приемной катушки 11 " , то на нее будут воздействовать все процессы, рассмотренные ранее, в результате чего в ней будут индуцироваться соответственно е M _м и е " _э, имеющие аналитические представления, аналогичные соответственно ^е мм ^{и e} м з .

Использование рассмотренных физических процессов позволяет получить в ферромагнитной системе 1 модулятора два варианта распределения стоячей магнитоэлектрического волны по длине этой системы:

– на всей длине ферромагнитной системы укладывается 3/2 длины X стоячей МЭ-волны 3, а ее средняя пучность 4 располагается по центру ферромагнитной системы 1 (см. рис. 2);

– на всей длине ферромагнитной системы 1 укладывается одна длина X стоячей МЭ-волны 3, а средний узел этой волны 5 располагался на поперечной оси симметрии ферромагнитной системы 1 (см. рис. 2).

Первый вариант распределения магнитоэлектрической волны соответствует функционированию модулятора для работы феррозонда в режиме градиентомера, при котором измерительными катушками будут регистрироваться соответственно ^{( + e} мм ),^{( + e} Mэ ) ^{и ( + e} мм ), ^{( + e} Mэ ), ^а второй вариант распределения обеспечивает функционирование модулятора для работы феррозонда в режиме полемера, при котором измерительными катушками будут регистрироваться соответственно ( + e "^), ^{( + e} "э ) ^{и ( + e} "м ),^{( - e} "э ).

Тогда для работы феррозонда в режиме гра-диентомера можем записать еГ = (eмм -eмм)+ (eмэ -eмэ) = ^мм,   (12)

^{где e} мм * ^e мм , ^e мэ = ^e мэ .

Соответственно для работы феррозонда в режиме полемера будет справедливо выражение вида es =(eмм + емм)+ [eмэ + (-емэ)] = 2eмм, (13) где eмм = e"м = eмм , Iемэ| = eмэ|-

Приведенные аналитические выражения (10)–(13) убедительно доказывают состоятельность предложенных идей, реализуемых в форматах предлагаемого способа и конструктивных особенностей устройства его реализации.

Все рассматриваемые физические процессы, лежащие в основе нового способа возбуждения феррозонда и обусловленные определенной совокупностью взаимосвязанных физических эффектов, представлены в виде соответствующей физической схемы феррозонда, показанной на рис. 4.

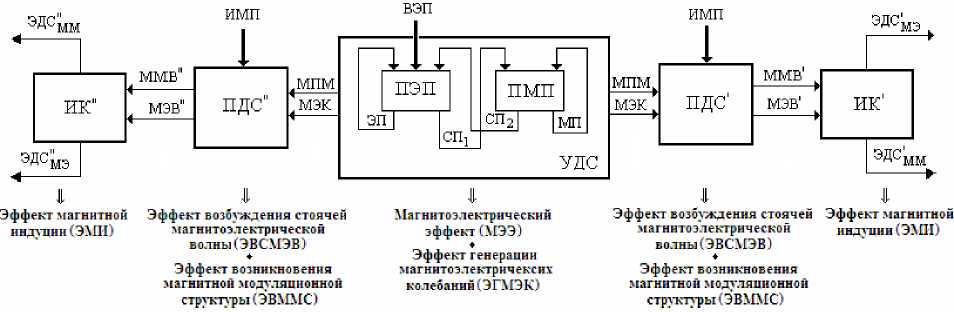
Рис. 4. Физическая схема феррозонда

На рис. 4 обозначено: ВЭП – внешнее электрическое поле; ИМП – измеряемое магнитное поле; УДС – упорядоченная доменная структура, состоящая из пьезоэлектрической и пьезомагнитной подсистемы соответственно ПЭП и ПМП; ЭП и СП₁ – соответственно электрическое и силовое поля, возникающие в ПЭП; МП и СП₂ – соответственно магнитное и силовое поля, возникающие в ПМП; МПМ – магнитное поле магнита; МЭК – магнитоэлектрические колебания; ПДС ′ и ПДС ″ – периодические доменные структуры соответственно первого и второго ферромагнитных стержневых полуэлементов (ФСП) модулятора; ММВ ′ и ММВ ″ – магнитомодуляционные волны соответственно в первом и во втором ФСП модулятора; МЭВ ′ и МЭВ ″ – магнитоэлектрические волны соответственно в первом и во втором ФСП модулятора; ИК ′ и ИК ″ – измерительные катушки феррозонда, расположенные соответственно на первом и втором ФСП модулятора; ЭДС ′ _ММ и ЭДС ″ ММ – магнитомодуляционные э.д.с. соответственно измерительных катушек ИК ′ и ИК ″ ; ЭДС ′ МЭ и ЭДС ″ МЭ – магнитоэлектрические э.д.с. соответственно измерительных катушек ИК ′ и ИК ″ .

Данная схема дает наглядное представление о существующих взаимосвязях между физическими процессами в различных функциональных подсистемах феррозонда (УДС; ПДС ′ ; ПДС ″ ; ИК ′ ; ИК ″ ):

• 1.    По отношению к УДС экзогенным физическим фактором является ВЭП, а эндогенными физическими факторами – ЭП, МП, СП 1 , СП 2 , которые в своей совокупности порождают физические эффекты МЭЭ и ЭГМЭК:

• 2.    По отношению к ПДС ′ и ПДС ″ экзогенными физическими факторами являются ИМП, МПМ, МЭК, которые в своей совокупности порождают физические эффекты ЭВСМЭВ и ЭВММС, проявляющиеся в виде эндогенных физических факторов {МЭВ ′ , ММВ ′ } и {МЭВ ″ , ММВ ″ }:

• 3.    По отношению к ИК ′ и ИК ″ экзогенными физическими факторами являются соответственно {ММВ ′ , МЭВ ′ } и {ММВ ″ , МЭВ ″ }, которые в своей совокупности порождают физические эффекты ЭМИ, проявляющиеся в генерации соответственно {ЭДС ′ ММ , ЭДС ′ МЭ } и {ЭДС ″ ММ , ЭДС ″ МЭ }:

F 1 : {ВЭП} → {МЭЭ ∧ ЭГМЭК} ⇒ {МЭК}.

F 2 : {МПМ; МЭК} → {ЭВСМЭВ} ⇒

⇒ {МЭВ ′ ∈ ПДС ′ ; МЭВ ″ ∈ ПДС ″ };

F 3 : {ИМП ∧ МПМ; МЭК} → {ЭВММС} ⇒

⇒ {ММВ ′ ∈ ПДС ′ ; ММВ ″ ∈ ПДС ″ }.

F 4 : {ММВ ′ ; МЭВ ′ } → {ЭМИ ∈ ИК ′ } ⇒

⇒ {ЭДС ′ ММ , ЭДС ′ МЭ };

F 5 : {ММВ ″ ; МЭВ ″ } → {ЭМИ ∈ ИК ″ } ⇒

⇒ {ЭДС ″ ММ , ЭДС ″ МЭ }.

Предложенная физическая схема феррозонда, наглядно показывающая взаимосвязь физических процессов, лежащих в основе предложенного способа возбуждения феррозонда, позволяет разрабатывать различные схемно-аппаратные варианты модуляторов для реализации процесса возбуждения феррозонда.

Экспериментальные исследования

Для экспериментального подтверждения работоспособности и эффективности нового метода возбуждения феррозондов был использован специальный макет стандартного поля (МСП) класса 0.1, имеющий значительно меньшие размеры, чем обычный компенсатор, выполненный на кольцах Гельмгольца, но при этом создающий магнитное поле с той же равномерностью [26].

В используемом МСП равномерное поле создавалось посредством системы колец (система Максвелла), состоящей из двух основных и двух дополнительных малых колец, расположенных по одной оси с основными кольцами (рис. 5). Эта система характеризуется расположением секций на поверхности общей сферы радиуса R 0 , т. е. выполнением условия R_i ² + a_i ² = R ₀ ² . В качестве расстояния от произвольной точки до оси системы приня-_„  /22

та величина ρ = x + y , где x и y – декартовы координаты.

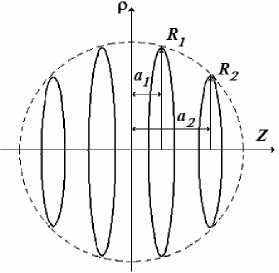
Рис. 5. Система колец тока (система Максвелла)

Обмотки основных и дополнительных колец включались последовательно и встречно. Диаметр основных колец и расстояние между ними выби- рались произвольно из геометрических размеров имеющегося рабочего пространства, а расстояние между дополнительными кольцами и их диаметр определялись однозначно из условия создания в объеме радиуса r магнитного поля с заданной равномерностью. В рабочем пространстве МСП помещался макетный образец феррозонда, техниче- ские характеристики которого определялись по результатам измерений его реакции на различные воздействия эталонных магнитных полей. С помощью МСП в процессе экспериментальных исследований макетного образца феррозонда создавались постоянные магнитные поля, величины которых варьировались в диапазоне от 0,5γ до 1000γ.

Напряженность магнитного поля заданной величины H кругового витка с током на оси задава- лась в соответствии с выражением u i n • i • Ri

П = — •------------:— .

2 ( z ² + R ²)³ / ²,

где N · I – число ампер-витков; Ri – радиус витка; z – расстояние от центра витка до интересуемой точки.

При градуировке методические и другие ошибки сводились к минимуму благодаря обработке результатов наблюдений по методу наименьших квадратов. При линейной интерполяции градуировочных характеристик чувствительность феррозонда определялась по формуле nn

S = £ U_tI_t A £ i f,                   (15)

i = 1        / i = 1

где Ui – выходное напряжение феррозонда при i- м измерении; Ii – ток в кольцах Гельмгольца; А – постоянная колец; n – количество точек градуировочной характеристики.

Систематическая погрешность (смещенный нуль) выявлялась в результате поворотов феррозондов на 180° в объеме скомпенсированного или почти скомпенсированного геомагнитного поля и вычислялась в соответствии с выражением ⁿ

• ⁵ = 2n_S Z ( U 0 + U 180 h               (16)

где S – чувствительность феррозонда; U 0 и U 180 – выходные напряжения феррозонда, соответствующие положительному и отрицательному значениям остаточного поля при каждом - м наблюдении; n – количество наблюдений.

В процессе экспериментальных исследований были определены следующие основные параметры феррозонда: 1 - предел измерения ±150 y ; 2 - порог чувствительности 0,5 у ; 3 - чувствительность 0,2 в/ у ; 4 – среднеквадратичное значение флуктуаций нуля при многосуточных наблюдениях 1^2 у ; 5 - температурный коэффициент не более 0,1 % на 1 °С; потребляемая мощность 20 мВт.

Заключение

В работе показано, что использование не-скомпенсированных ферромагнетиков (ферримагнетиков), к которым относятся ферриты, имеющие сложную структуру кристаллической решетки, состоящую из двух и более подрешеток, и наличие косвенного обменного взаимодействия обеспечивает при определенных условиях возможность появления в таких структурах на микроуровне резонансного МЭЭ, обладающего одновременно поляризующим и намагничивающим свойствами. Это вызывает существенные изменения как связанных колебаний намагниченности подрешеток, так и изменение энтропии косвенного обменного взаимодействия, что в конечном счете приведет к появлению соответствующих электродинамических процессов уже на макроуровне.

Таким образом, возбуждаемый посредством переменного электрического поля в структуре ферримагнетика магнитоэлектрический эффект на частоте совпадения электромеханического и магнитного резонансов используется в качестве механизма трансформации однородно упорядоченной доменной структуры в динамическую периодическую доменную структуру, распределенную вдоль всей длины ферритового стержня и формирующую при этом стоячую магнитную волну. В данном случае в МЭЭ важен не сам факт присутствия традиционной макроуровневой магнитострикции, а инициация в структуре ферромагнетика локального (элементарного) МЭЭ, представляющего собой динамическую неоднородность, при перемещении которой происходит одновременно активное опосредованное полевое взаимодействие через доменные структуры с чувствительными элементами феррозонда и соответствующая параметрическая модуляция магнитной проницаемости материала ферримагнетика, которая приобретает осциллирующие свойства.

Конструктивно и технологически феррозонд с новым способом возбуждения выгодно отличается от традиционных феррозондов, у которых обязательным возбуждающим конструктивным элементом является многовитковая электрическая обмотка катушки. Протекающий переменный электриче- ский ток через обмотку многовитковой катушки вызывает соответствующий процесс ее теплового нагрева, который является заметным дестабилизирующим фактором режима функционирования феррозонда при его эксплуатации. Кроме того, необходимость применения многовитковой катушки создает определенные технологические сложности при изготовлении феррозонда и ограничения в варьировании параметров возбуждающего магнитного поля (амплитуды напряженности и частоты), а также вызывает существенное увеличение его массогабаритных параметров и стоимости. Применение вместо возбуждающей многовит-ковой катушки конденсатора с профильными электродами, создающего возбуждающее пе- ременное электрическое поле, фактически устраняет все перечисленные недостатки, свойственные традиционным феррозондам, что фактически обеспечивает конкурентное преимущество предлагаемого нового типа феррозонда.

На основе предлагаемого способа возбуждения феррозондов и базовой конструкции устройства его осуществления открываются широкие возможности для исследований в области нового направления в науке – спинтроники, в частности, прикладного использования МЭ-взаимодействия, которое разработчики магнитометрической аппаратуры могут эффективно использовать при создании различных вариантов феррозондов на новых физических принципах функционирования.