Fig (Ficus Carica L.) Identification Based on Mutual Information and Neural Networks

• I.    INTRODUCTION

  The computerization of plant management species becomes more popular. The process of recognition and identification of plant species is very time-consuming as it has been mainly carried out by botanists. The focus of computerized living plant identification is on stable feature’s extraction of plants. The information of leaf plays an important role in identifying living plants. Leaf-based features are preferred over owner’s fruits, etc. due to the seasonal nature of the later and also the abundance of leaves. Fig ( Ficus Carica L .) tree plays an important role in the Syrian economy, where Syria produces 42944 tons a year. For this reason, the classification of fig tree species is of paramount

importance to preserve type and improve production. In this research, we described the classification of a plant Fig ( Ficus Carica L) with multiple varieties. Fig is one of the oldest fruit trees in the Mediterranean zone. Its wild genetic resource still exists in many countries, including Syria and Anatolia, which are considered as the natural habitats of the fig tree.

The classification of plant leaf has been introduced in several approaches such as k-Nearest Neighbor Classifier (k-NN), Probabilistic Neural Network (PNN), Genetic Algorithm (GA), Support Vector Machine (SVM), and Principal Component Analysis (PCA) [1]. Zulkifli [2] proposed General Regression Neural Network to classify 10 kinds of plants with green color leaves. Wu et al. [3] used PNN to classify 32 kinds of green leaves. Singh et al. [4] suggested SVM to implement a classifier for the problem. Shabanzade et al. [5] used Linear Discriminant Analysis (LDA). Several of researchers are used aspect ratio, leaf vein, and invariant moment to identify plant. Several features such as an aspect ratio (ratio between length and width of leaf), the ratio of perimeter to the diameter of leaf, and vein features were used to characterize the leaf with accuracy of 90 %. Wu et al. [3, 6]

On the other hand, Texture analysis is important in many applications of computer image analysis for classification, detection, or segmentation of images based on local spatial variations of the intensity or the color. Actually, shape, color and texture features are common features involved in several applications, such as in [7] and [8]. However, some researchers used part of those features only. Invariant moments proposed by Hue are very popular in image processing to recognize objects, including leaves of plants [9-10]. Polar Fourier transforms (PFT) proposed by Zhang [2]. Several leaf classification systems have incorporated texture features to improve the performance, such as in [12] that used entropy; homogeneity and contraction derived from the co-occurrence matrix came from Digital Wavelet Transform (DWT), in [13] that used lacunarity to capture the texture of leaf and in [14] that used GLCM.

Texture features can be extracted by using various methods. Gray-level Gabor Filter and Local binary pattern (LBP) are examples of popular methods to extract texture features.

To implement the preliminary classification system, in this research, we tried to capture the texture of the leaf by a new feature extraction technique based on mutual information. Those features were inputted into the identification system that uses a neural network classifier. Testing was done by using a data set. The result shows that method improves good performance (92%) of the identification system with 2 cultivars and 90 with 3 cultivars.

Mutual Information (MI) and Entropy provide an intuitive tool to measure the uncertainty of random variables and the information shared by them, in which the entropy and the mutual information are two critical concepts. The entropy is a measure of the uncertainty of random variables, while the mutual information is a measure of information shared by two random variables. MI can compute between two variables if we have explicit knowledge of the probability distributions. In general, these probabilities are not known. Various methods are used to estimate the probability densities from the observed data. In the next two sections, this paper treats a brief presentation of MI concept and the descriptor algorithm. In the section 4, the concept of neural networks Training Multilayer Perceptrons are described. Image analysis is given in sections 5. Results and discussion are presented in section 6. At the end, a conclusion is presented.

• II.    ENTROPY AND MUTUAL INFORMATION

The entropy H is a measure of the uncertainty of random variables. Let X is a discrete random variable with alphabet and p ( x ) = P ( X = x ), x eX be the probability mass function, the entropy of X is defined as:

H ( X ) = - £ p ⁽ x ) log p ⁽ x )                (1)

x eX

While the mutual information is a measure of information shared by two random variables, defined as:

I(X, Y)=Z Z p(x, y)log xeX yeY

p ( x , y ) p ( x ) p ( y )

= H ( Y ) - H ( Y | X ),                (2)

Where p ( x , y ) represents the joint probability distribution of (X, Y) , p ( x ) and p ( y ) are the marginal distributions of X and Y, respectively. H(Y|X) is the conditional entropy of Y in the case of X is known. It can be represented as:

H ( Y | X ) = - Z p ( x , У ) log p ( У I x ) (3)

x eX

For the continuous random variables, the entropy and the MI are defined as in (1), (2) and (3) after replaced the summation by integration. The MI is zero if and only if X and Y are statistically independent, i.e. vanishing mutual information does imply that the two variables are independent. This shows that MI provides a more general measure of dependencies in the data, in particular, positive, negative and nonlinear correlations.

We can compute the MI between two variables if we have explicit knowledge of the probability distributions. In general, these probabilities are not known. Various methods are used to estimate the probability densities from the observed data. Consider two sequences (S i ) and (S J ) of n simultaneous observations of two random variables. Since entropy is computed using discrete probabilities, we estimate probability densities using the widely used histogram method [16-20].

Let Fx(i) denote the number of observations of X falling in the bin a i . The probabilities p( a _i ) are then estimated as:

p( a i ) = f X X i l n

Let f_Y ( j ) denote the number of observations of Y falling in the bin b j . The p robabilities p( b j ) are then estimated as:

p( b j ) = ^ Y>n

Let f_XY ( i ; j ) denote the number of observations such as that X falls in bin a _i and Y falls in bin b _j . Then the mutual information between X and Y is estimated as:

I ( X , Y ) = log n +ly У f„ ( i ; J ) log f^i i j- (4) n _{i j} f _X ( i ) f _Y ( j )

• III.   NEW DESCRIPTOR BASED ON MUTUAL

INFORMATION .

In the following section, we describe our new Algorithm NDBMI for constructing the descriptor.

• 1-    Given a image (matrix) A( n , m), divide it in to sub images (matrices) S i (k, l), it gives a collection of sub images (matrices) P

• 2-    Find the mean matrix of the collection P

• 3-    Calculate the MI between each sub matrix in the collection P and the mean matrix; it gives a vector with dimension equal to cardinality of the collection.

• 4-    Consider the vector calculated in 3 as a descriptor of the image A.

• IV.   NEURAL NETWORKS

In the following sub section we present and review one of the important classes of ANN, which is the Feed Forward Neural Networks.

Artificial Neural Networks (ANNs) are massively parallel, highly connected structures consisting of a number of simple, non linear processing units. Due to their massively parallel structure, they can perform computation at very high rate if implemented on a dedicated hardware. Moreover of their adaptive nature, they can learn the characteristics of inputs signals and adapt to data changes. The nonlinear nature of ANNs can help in performing function approximation and signal filtering operations which are beyond optimal linear techniques.

A.    feed-forward artificial neural networks

Artificial neural networks are parallel computational models which are able, at least in principle, to map any nonlinear functional relationship between an input and an output hyperspace to the desired accuracy. They are constituted by individual processing units called neurons or nodes and differ among each other in the way these units are connected to process the information (architecture) and, consequently, in the kind of learning protocol adopted. In particular, the neurons of a feedforward neural network are organized in three layers: The input units receive information from the outside world, usually in the form of a data file; the intermediate neurons, contained in one or more hidden layers, allow nonlinearity in the data processing; the output layer is used to provide an answer for a given set of input values (Fig. 1).

In a fully connected artificial neural network, each neuron in a given layer is connected to each neuron in the following layer by an associated numerical weight Wij. The weight connecting two neurons regulates the magnitude of signal that passes between them. In addition, each neuron possesses a numerical bias term, corresponding to an input -o1 f whose associated weight has the meaning of a threshold value. Information in an ANN is stored in these connection weights which can be thought of as the “memory” of the system. The goal of back-propagation training is to change iteratively the weights between the neurons in a direction that minimizes the error E, defined as the squared difference between the desired and the actual outcomes of the output nodes, summed over the training patterns (training set data) and the output neurons, according to the steepest descent method:

∆ W ij ( k ) =- η ∂ ^E + α ∆ W ij ( k - 1) ∂ w_{i j}

The variation of a connection weight at the kth iteration depends on the partial derivative of the total error with respect to that weight through a proportionality constant termed learning rate (η) and on the variation of the same weight during the previous iteration by means of a momentum term (α). To compute the partial derivative of the error E with respect to the connection weights to the hidden layer(s) requires propagating backwards the prediction error E using the rules of chain derivation, hence, the name “back-propagation”: Chain derivation acts as a way to “distribute” the error E between the neurons of the hidden layer(s) in order to apply the iterative weight adjustment, necessary for the learning of the network [21–23].

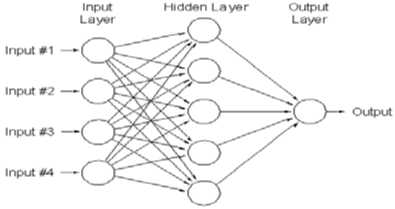
Figure 1 : Feed-forward Neural with three layers

B.    Training Multilayer Perceptrons

Once the number of layers, and number of units in each layer, has been selected, the network's weights and thresholds must be set so as to minimize the prediction error made by the network. This is the role of the training algorithms. Which are used to adjust automatically the weights and thresholds in order to minimize this error. This process is equivalent to fitting the model represented by the network to the training data available. The error of a particular configuration of the network can be determined by running all the training cases through the network, comparing the actual output generated with the desired or target outputs. The differences are combined together to form an error function which measures the network error. One of the error functions is the sum squared error. [24-28]

We are interesting to apply the Mutual Information computation to identify and classify the Figs (Ficus Carical) trees in Syria region. Each pattern (Fig leaf image) is described using varieties of numeric features, which is the features vector returned by the feature extraction function based on mutual information descriptor (section 3). The data set is divided into two sets, one for training, and one for testing. The preprocessing parameters were determined using the matrix containing all features which used for training or testing; these same parameters were used to preprocess the test feature vectors before passing them to the trained neural network.

A fixed number (m) of instances for each class were randomly assigned to the training set and the others instances from each class for testing set. The first preprocessing function was used to preprocess the networks training set, By normalizing the inputs and targets, they have means of zero and standard deviation of 1.The normalized training sets were used to train a Feed Forward Back Propagation network (with a number of inputs equal to the number of features (m), (2m+1) hidden neurons and 2 outputs neurons equal to the number of classes).

FM represents the instance features of the pattern (Fig leafs) that belongs to the class 1. The columns number d+1,d+2,d+3,….,2d, represents the instance features of the pattern (Fig leaf) which belongs to the class 2, etc. we rewrite the matrix FM as the form :

FM = lf. . for l = 1,.2,3,..,d ij i = 1,2,3,..,m, and j = 1,2,3,..,n

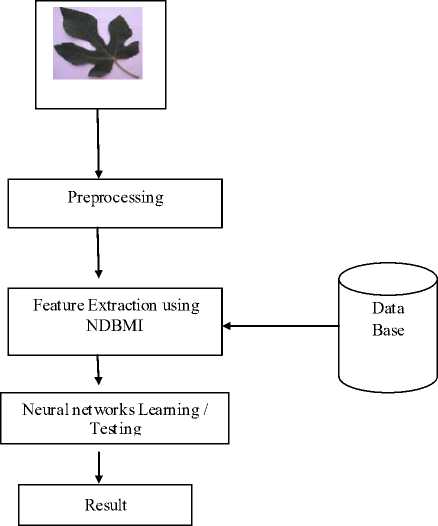
Figure.2 Model of the Leaf Classification System

For example when m = 6, d=2 and n =4, the outputs matrix OM will be as the fowling form (The neurons number of the input layer is equal 6, and the output layer is equal 4)

OM =

Also we represent all features for the testing set in a matrix TM each column represents the pattern feature. If the testing set contains dT instances for each pattern that belongs to the same class, The dimension of the matrix TM will be equal to ^{m x dT x n} where m is the number of features (dimension of feature vector) and n is the number of classes we rewrite the matrix TM as the form [29].

TM =^l f _ij for l = 1,.2,3,..,. dT

i = 1,2,3,...., m , and j = 1,2,3,..., n

• VI.    RESULTS AND DISCUSSION

Fourty Two adult leaves of FIG were harvested from three trees in the same day all the leaves were chosen by experts in the same way, from those at a mature stage, showing no damage. The image of inferior leaf sides was only used, that is low resolution digital image. The momentum and learning rate were 0.9 and 0.01 respectively ( n , a in the equation 1).

The output of the Neural Network is represented by a vector that belongs to [0, 1]n, where n is equal to the number of neurons in the output layer. It is also equal to the number of classes (2 or 3). For n = 2, if the output vector is (0, 1)^T then the networks classifies the pattern to the class two. The output vector should contain a one and only a one, Otherwise to the class one. We represent all features for the learning set in a matrix FM. Each column represents the pattern feature. If the learning set contains d instances for each pattern that belongs to the same class, the dimension of the matrix FM will be equal to m x d x n where m is the number of features (dimension of feature vector) and n is the number of classes. The columns number 1, 2, 3,…, d in the matrix

Figure.3 Example of image Fig tree class 1 (shaghoury)

Figure.4 Example of image Fig tree class 2 (Dir Attia)

Figure.5 Example of image Fig tree class 3 (Maysony)

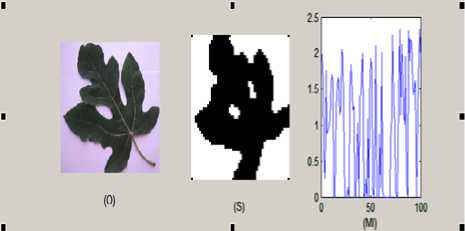
Figure. 8 O: original Image S: Segmented image, MI: mutual information of S of size 50x50.

Testing set contains 7 pattern for each class, and the Learning set contains 7 patterns for each class (The total is equal to 21 patterns).

The Block diagram of the classification system is shown in figure 2. First of all, the leaf is inputted to the system. Preprocessing does such as converting RGB image to Gray image, filtering, segmentation then the features of the leaf are extracted by using NDBMI, which are used by neural system classifier. (Figures 7, 8 and 9)

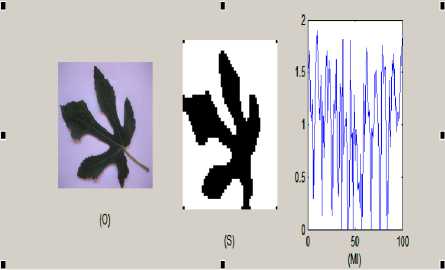
Figure. 6 O: original Image S: Segmented image, MI: mutual information of S of size 50x50.

We are appalling the NDBMI descriptor by using the image size 100x100 and 5x5 sub images, and then we have a feature vector size 400. See Fig. 10

Figure. 9 MI: mutual information of S of size 100x100.

The experiments were accomplished by using three kinds of FIG trees. Firstly, we are using three pairs of types. Type 1 with type 2, type 2 with type 3, and type 3 with type1. Secondly, we are using the three types together.

The accuracy of the system is calculated by using the following equation:

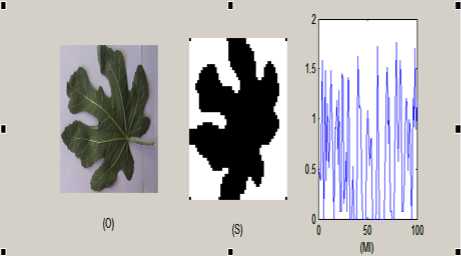
Figure. 7 O: original Image S: Segmented image, MI: mutual information of S of size 50x50.

n

Accuracy = ^r n _t

, where n_r is the numbers of correct leaves classify and n_t is the total number of leaves.

We were obtained accuracy 92.6 % for the classification rate over all the two types classification and accuracy 90% for the 3 types.

The results are showing in figures 12 and 13 for two-class classification, where figures 14 and 15 show the classification of the three classes.

Neural output Matrix with Learning set

2       4       6       8       10      12      14

Figure 10-Testing with data Learning (two classes)

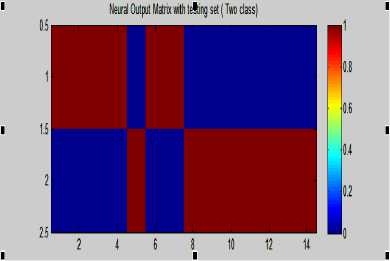
Figure 14- Neural out matrix with Testing set (two classes)

Out NN: with 500 iterations

0.99 0.99  0.99  0.96 0.92 0.94  0.80 0.26  0.85 0.74

0.94   0.88 0.81 0.65

0.29  0.06  0.97  0.99 0.36 0.90  1.00 1.00 0.98  1.00

0.97 0.94 1.00   0.96

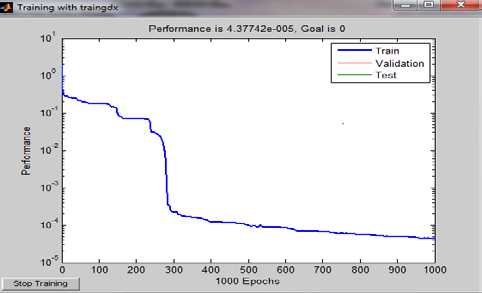
Figure 11 : Performance Neural networks out after 1000 iterations.

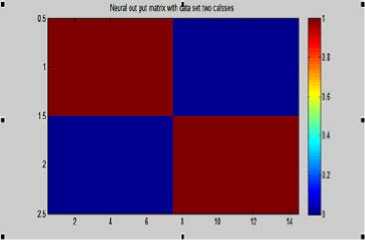
Figure 15- Neural out matrix with Testing set (two classes) (100% Maysony /shaghoury)

Neural output Matrix with testing set

8      10      12      14

Figure 12- Neural out matrix with Testing set (two classes) 92.8 % Dir Attia/shaghoury

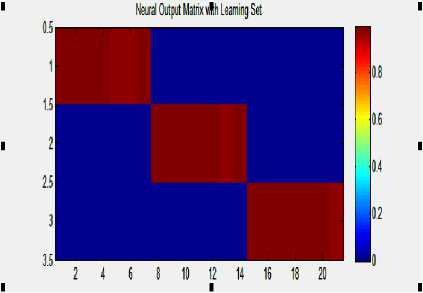
Figure 16- Neural out matrix with Learning set (3 classes)

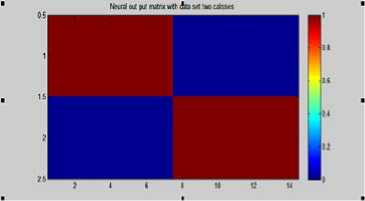
Figure 13- Neural out matrix with Testing set (two classes) 100% Dir Attia/shaghoury

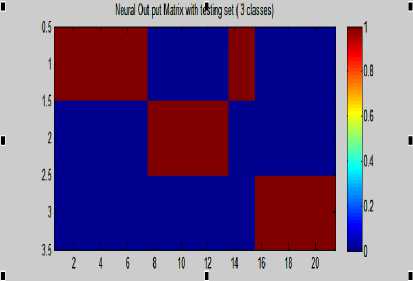
Figure 17- Neural out matrix with testing set (3 classes)

90.4%

VII. C ONCLUSION

We study and propose new descriptor based on mutual information theory, which used as input to neural

networks classifier for classification Fig (Ficus Carica L) trees. We use two hidden layer feed forward neural networks. The proposal technique is applied to set of 42 samples (3 classes) 14 image for each class. 7 Images of each class are used for the network training and the remaining images are used for generalization and testing. The patterns (images) were described using a new descriptor based in mutual information. The result shows that the recognition rates were 100% for the training and 92.8% for generalization. The preliminary results obtained indicated the technical feasibility of the proposed method that will be applied for more than 120 varieties existent in Syria