Фильтрация оценок вектора состояния в двухпозиционной радиолокационной системе с применением искусственных нейронных сетей

Несмотря на значительный прогресс в разработке основных элементов и устройств радиолокационных систем (РЛС) (антенн, передатчиков, приемников, устройств обработки информации), случаях возросшие требования к ним не удается реализовать при использовании однопозиционной РЛС, поэтому возникает задача совершенствования принципов построения радиолокационных станций и систем.

Одним из перспективных направлений является переход от однопозиционных РЛС к многопозиционным радиолокационным системам (МП РЛС), состоящим из разнесенных в пространстве передающих и приемных пунктов (или однопозиционных РЛС), совместно ведущих радиолокационное наблюдение целей [1; 2]. В МП РЛС радиолокационная информация (РЛИ) используется более эффективно.

Анализ сведений, приведенных в отечественных и зарубежных работах, позволяет сделать вывод о том, что для реализации возможностей МП РЛС требуется решение комплекса взаимосвязанных теоретических и практических задач.

Значительное расширение практической реализации результатов теоретических исследований возникает благодаря внедрению в радиолокационное оборудование цифровых методов обработки сигналов. Эффективные результаты достигнуты в области разработки быстродействующих, устойчивых к вычислительным погрешностям алгоритмов вторичной обработки [3]. Анализ применения линейных рекуррентных алгоритмов оценивания координат цели в МП РЛС и вопросов повышения ее точностных характеристик за счет объединения координатной информации проводился в работах [1; 2].

Объединение этих направлений с централизованной вторичной обработкой информации позволяет создать оптимальную многопозиционной систему Вместе с тем оптимальной многоканальной фильтрации присущи и следующие недостатки [3]:

• -    возможность работы только в централизованном режиме;

• -    большой объем вычислительных операций в пункте обработки информации для определения параметров траектории цели;

• -    необходимость передачи из приемных пунктов в пункт обработки информации всего объема получаемой информации;

• -    низкая живучесть;

• -    необходимость предварительного приведения оценок приемных пунктов к единой системе координат и т. д.

Построение оптимальной МП РЛС вызывает определенные трудности. Поэтому анализ известных и разработка новых алгоритмов децентрализованной вторичной обработки РЛИ для МП РЛС, обеспечивающих высокую точность оценивания координатной информации, является актуальной задачей.

В качестве многопозиционной радиолокационной системы авторы предлагают использовать двухпозиционную радиолокационную систему с децентрализованной вторичной обработкой РЛИ. Выбор такого упрощенного варианта системы обусловлен тем, что основные закономерности многопозиционного приема в полной мере проявляются и в двухпозиционной системе. При этом МП РЛС значительно проще в технической реализации. Кроме того, они сохраняют преимущества по повышению точности определения координат целей и помехозащищенности перед однопозиционными РЛС.

В представленной статье осуществляется анализ двух вариантов децентрализованной системы обработки координатной информации, состоящей из рекуррентных алгоритмов фильтрации координат цели, в вынесенных приемных пунктах (ВПП). В первом варианте обработки сглаженные оценки координат цели по линиям связи из ВПП передаются в пункт обработки информации (ПОИ), в котором осуществляется их комплексирование (ФО-алгоритм).

Во втором варианте повышение точности прогнозируемой оценки вектора состояния осуществляется за счет использования технологии искусственных нейронных сетей (ИНС) [5].

Алгоритм ФО используемый в первом варианте , основан на децентрализованной обработке данных [1; 4]. Рациональное распределение этапов обработки РЛИ позволяет сократить часть вычислительных затрат путем перехода к многомашинной вычислительной структуре. Непосредственное сопряжение ЭВМ с каждым приемным пунктом дает возможность уменьшить число вычислений в ПОИ путем частичной обработки информации на месте [4].

Первый этап децентрализованной обработки реализуется непосредственно на ВПП и заключается в самостоятельном определении оценки вектора состояния a _k по каждой из совокупностей оценок вектора наблюдаемых параметров X , где к - номер такта измерения.

Модель косвенного измерения координат аэродинамической цели является линейной:

Xk = hk [ак ]+5k, (1) где h [ak ] - нелинейная функция пересчета вектора состояния в вектор наблюдаемых параметров; 5к - вектор ошибок измерений, элементы которого являются белым шумом.

В настоящее время общая теория оптимальных методов статистической обработки информации в нелинейных задачах разработана достаточно хорошо [1], однако практическое применение результатов этой теории сопряжено с большими трудностями. В связи с этим часто отдают предпочтение построению субоптимальных фильтров, рационально сочетая необходимую эффективность их функционирования и допустимую сложность применительно к решению практических задач.

В качестве приближенных рекуррентных алгоритмов нелинейного оценивания часто применяются различные модификации линейных рекуррентных алгоритмов. Фильтры Калмана (ФК) в классе линейных рекуррентных алгоритмов обеспечивают оценивание вектора состояния динамического объекта с минимальной среднеквадратической ошибкой (СКО).

В основу построения алгоритмов фильтра Калмана положены концепции предсказания координат цели и коррекции этих координат на основе полученных данных. При использовании линеаризованных фильтров Калмана качество оценки вектора состояния во многом зависит от близости оценки и истинного значения вектора состояния. Поэтому расчет h_k [ a _k ] целесообразнее проводить относительно оценки, полученной к моменту поступления очередного измерения.

Алгоритмы дискретного фильтра Калмана могут быть представлены в следующем виде:

• -    алгоритм оценивания вектора состояния

а k = а k/k-1 + Kk {( k - hk [a k/k-1 ]};(2)

• -    алгоритм одношагового предсказания

a k/k-1 = Bk-1ak-1 ;(

• -    вычисление матричного коэффициента усиления

Kk = Ck-1 h-;;(4)

• -    алгоритм вычисления апостериорной матрицы ошибок измерений вектора состояния

• -    алгоритм вычисления априорной матрицы ошибок измерений вектора состояния

с - k - 1 = B k - 1 с ;! BL + Q k - 1 ;            (6)

где h_k [cz _k / _k 1 ] - пересчет прогнозированной оценки вектора состояния в сферическую систему координат; B_k , H_k , Q_k - известные матрицы.

Вычисления, произведенные с помощью уравнений фильтрации (2).. .(6), осуществляются на основании результатов двух первых радиолокационных измерений: ( 1 , ( 2 - для упрощенного фильтра Калмана (УФК) и трех измерений: ( , ( 2 , ( 3 - для расширенного фильтра Калмана (РФК). Это связано с необходимостью вычисления оценок скорости и _xk , и _yk , и _zk для УФК и дополнительно оценок ускорений 5 _xk , 5 _yk , 5 _zk для РФК. Составляющие оценки вектора состояния могут быть рассчитаны только на основании оценок вектора наблюдения, полученного в различные моменты времени. Матричный коэффициент усиления K_k и матрица дисперсий ошибок оценивания вектора состояния C k - ¹ для обобщенного фильтра Калмана не могут быть вычислены заранее. Вычисление этих величин должно происходить в реальном масштабе времени, так как они, в соответствии с процедурой линеаризации, зависят от текущей оценки вектора состояния a _k .

Выражения (2).. .(6) описывают алгоритмы получения оценки вектора состояния a _k и корреляционной матрицы ошибок измерения C k ^{- 1} в момент поступления данных на к -м шаге.

Разность между текущей и прогнозируемой оценкой вектора наблюдаемых параметров равна .

^V k = ⁽ k ^- hk ^{[ а} k / k - 1 ] .                   (7)

Величина v _k , которую называют невязкой, умножается на матричный коэффициент усиления K_k , в результате чего формируется сигнал коррекции. Далее этот сигнал суммируется с предсказанной оценкой вектора состояния a _k / _k - 1 , в результате чего получается оценка вектора состояния в ВПП.

Оценки вектора состояния в ВПП представлены в единой форме записи и привязаны к одному моменту времени. Для формирования результирующей оценки век-

C k ^{- 1} = ( C k / k - 1 + H T C xk H k )^{- 1} ;            (5)

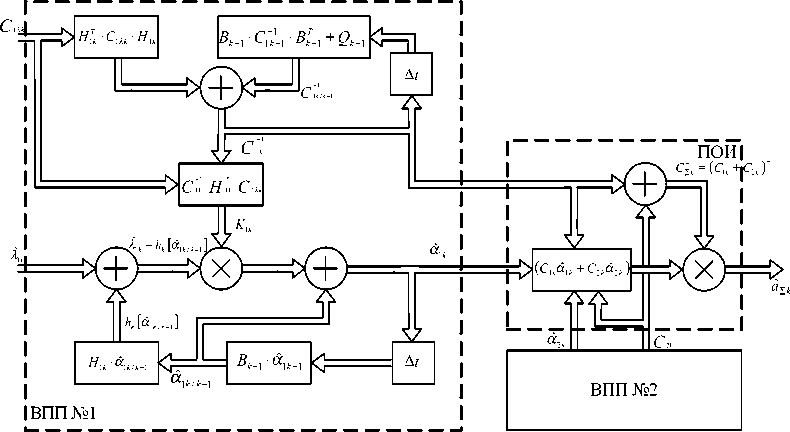
Рис. 1. Структурная схема алгоритма ФО

тора состояния « хk необходимо иметь статистические характеристики отдельных оценок. Исчерпывающей статистической характеристикой каждой оценки параметров траектории является ее ковариационная матрица C ik . Результирующая оценка вектора состояния сводится к выполнению простой операции статистического согласовании [4]

^a х k = C X ( C i k ^C 1 k + C 2 k ^C 2k ) , (8) где a 1 _k, a _2k - оценки вектора состояния в 1-м и 2-м ВПП; C 1 k , C 2 k - соответствующие корреляционные матрицы точности; C _x k = ( C 1 _k + C 2 _k ) ^{- 1} - результирующая матрица ошибок.

Схема реализующая алгоритм децентрализованной обработки данных (2).. .(6), (8), имеет следующий вид (рис. 1).

Повышение точности прогнозирования во втором варианте алгоритма вторичной обработки РЛИ приводит к созданию нового фильтра с нейронной сетью на основе фильтра Калмана (ФНС). В ФНС происходит замена прогнозированного значения фильтра Калмана B_k_!& _k _ 1 на прогнозированное значение, сформированное нейронной сетью. В остальном работа фильтра осталась неизменной.

Разработанный дискретный фильтр отличается от обычного ФК (2)...(6) только алгоритмом одношагового предсказания (3):

^a kp - 1 = ^a k - 1 ^{+ Aa} Yk . ⁽⁹⁾

Матричный коэффициент усиления Kk и матрица дисперсий ошибок оценивания вектора состояния C— для ФНС, как и для фильтра Калмана, не могут быть рассчитаны заранее. Вычисление должно происходить в ре альном масштабе времени, так как эти величины зависят от текущей оценки вектора состояния ak.

Выражения (2), (4)...(9) описывают алгоритмы получения оценки вектора состояния a _k и корреляционной матрицы ошибок измерения Ck¹ в момент поступления данных на к -м шаге (рис. 2). Выражение a _k/_k _ 1 соответствует экстраполяции оценки вектора состояния, полученной на предыдущем шаге.

Формирование начальных данных для работы нейронной сети и вычисление прогнозированной оценки вектора состояния осуществляется следующим образом.

Оценка вектора наблюдаемых параметров X _k , поступающая на каждом такте измерения, и отфильтрованная оценка вектора состояния a _k _ 1 позволяют сформировать вектор

Ka fk = ( Z_k ( Л _к ) - a k _ i ) (10)

между текущей оценкой Zk (Xk) вектора наблюдения, пересчитанной в декартову систему координат и отфильт рованной оценкой вектора состояния на предыдущем (к - 1) шаге фильтрации ak_1. При использовании обученной сети в ФНС вычисление Atxfk возможно с исполь зованием оценок координат вектора состояния вместо вектора наблюдений. При этом необходимо, чтобы последний вектор Act 1 k вычислялся с использованием принятого вектора наблюдений на к-м шаге. Данный вектор поступает на вход нейронной сети с предыдущими тремя векторами Atxk = [Aa4k; Aa3k; Atx2k; Aa1 k ]T. На выходе нейронной сети формируется значение следующего вектора AtxYk = (AxYk, AyYk, AzYk)T и определяется оценка вектора состояния координат цели, состоящая из оценок век тора координат

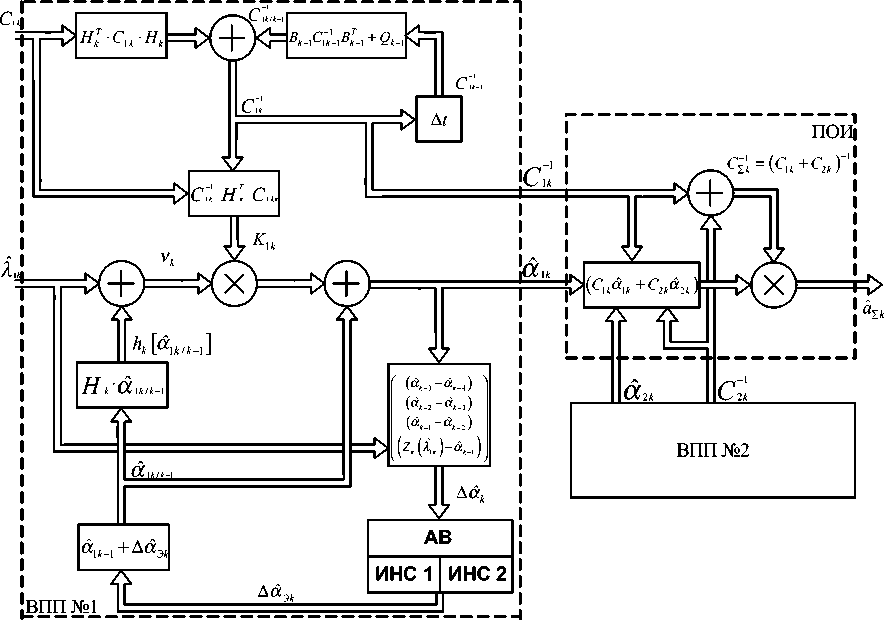
Рис. 2. Структурная схема алгоритма ФО-ФНС. АВ - алгоритм выбора; ИНС1 - нейронная сеть, обученная на равномерное прямолинейное движение цели; ИНС2 - нейронная сеть, обученная на движение цели с маневрами

а-1(1:3) = xkp-1 ykp-1 _ С      X xk-1 А Ук-1 А С zk-1 J + -Ai „ ’ Ay „ A J (11) А z V k/k-1 и оценок вектора скоро* стей f Ci Uxkp -1 fAXyk / T) аkp-1(4:6) = Uvk k-1 Uzk/k-1 _ Ay yk Д7 . z Ýk / T / T J (12) соответствующих к-му такту измерений. Этот вектор аналогичен вектору прогнозированного значения ak / k_,, который вычисляется в упрощенном фильтре Калмана. Он содержит прогнозированные оценки координат и скоростей цели.

Разработанный ФНС-алгоритм оценивания координат цели может быть использован в МП РЛС аналогично фильтру Калмана в ФО-алгоритме. В ФО-алгоритме результирующая оценка вектора состояния оа ^ _k на выходе ПОИ формируется путем комплексирования оценок векторов состояния с А 1 _k и 6 ( 2 _k . Комплексирование оценок координат цели, вычисленных в вынесенных приемных пунктах по ФО-ФНС-алгоритму, происходит в ПОИ по алгоритму (8).

Структурная схема ФО-ФНС-алгоритма (см. рис. 2) аналогична структурной схеме алгоритма ФО (см. рис. 1), за исключением блока, рассчитывающего Ac A _k , и блока АВ, определяющего в зависимости от модели движения, какая ИНС должна прогнозировать Ac A y _k : ИНС1 обучена на прогнозирование вектора A c t y _k при оценивании координат цели, летящей равномерно прямолинейно, ИНС2 применяется если цель движется - с маневрированием по направлению или скорости.

Моделирование работы алгоритма фильтрации ФНС в двухпозиционной радиолокационной системе (ФО-ФНС) позволило провести сравнительный анализ между алгоритмами фильтрации ФО и ФО-ФНС.

Проведенное имитационное моделирование ставило перед собой задачу исследования эффективности применения линейных рекуррентных алгоритмов фильтрации с целью повышения точности оценивания координат аэродинамической цели. Результаты моделирования процесса оценивания координат аэродинамической цели с помощью алгоритмов фильтрации ФО (кривые 1) и ФО-ФНС (кривые 2) представлены на графиках зависимости СКО фильтрации координат цели от номера шага фильтрации в декартовой системе координат (рис. 3.5).

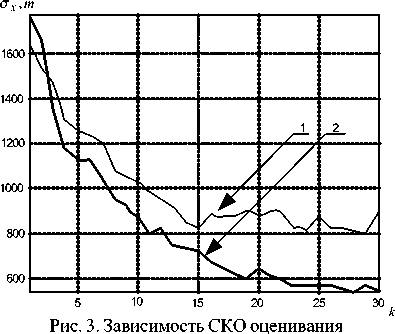
по координатеАпри равноускоренном движении

Применение синтезированного алгоритма ФО-ФНС повышает точность оценивания по отношению к известному ФО-алгоритму на20.40 % в установившемся режиме.

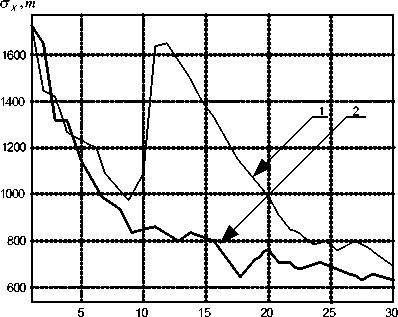
Рис. 4. СКО оценивания по координате А’ при маневрировании по скорости

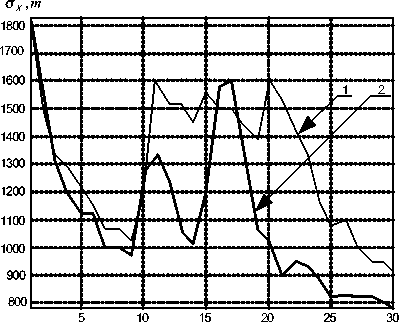
Рис. 5. СКО оценивания по координатеА при маневрировании по направлению

Таким образом, на основании вышеизложенного можно сделать следующие выводы:

• 1.    Применение децентрализованного алгоритма обработки РЛИ (ФО) позволяет повысить точность оценивания координат цели по сравнению с бистатической РЛС на 20.30 %.

• 2.    Исследование применения нейрокомпьютерных алгоритмов ИНС в радиолокации позволяет сделать вывод о возможности ее использования для повышения точности оценивания координат цели в ВПП.

• 3.    Разработанный алгоритм вторичной обработки РЛИ с применением искусственных нейронных сетей (ФНС) позволяет повысить точность оценивания координат цели за счет повышения точности прогнозированной оценки вектора состояния по сравнению с ФК на 20.40 %.

• 4.    Проведенный анализ чувствительности и устойчивости алгоритма ФНС к изменению внешних и внутренних параметров показал, что разработанный фильтр позволяет следить за целью во всем диапазоне скоростей и на всех видах траекторий и маневров, которые были учтены в задачнике на этапе обучения НС.

• 5.    Полученные результаты в ходе сравнительного статистического анализа алгоритмов децентрализованной обработки (ФО, ФО-ФНС) позволяют сделать вывод о том, что

• повышение точности оценивания координатной информации в установившемся режиме для ФО-ФНС-алгоритма по сравнению с ФО-алгоритмом составляет 20.. .40 %.