Фильтрационные процессы при боковой экструзии флюидонасыщенных поропластов

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2019PNRPU MECHANICS BULLETIN

Установившиеся течения пластических сред в каналах рассматривались во многих работах начиная с середины XX века. Преимущественно речь шла о сужающихся плоских или осесимметричных каналах, тем самым моделировался достаточно давно известный процесс обработки материалов – прямая экструзия (Соколовский, 1950 [1] – ассоциированный с поверхностью текучести Мизеса закон; Shield, 1955 [2] – призма Треска, гипотеза Хаара–Кармана; Danyluk, 1969 [3] – упруго-пластическая задача в рамках теории Прандтля– Рейсса при условии текучести Мизеса; Aleksandrov, Barlat, 1999 [4] – течение через осесимметричный канал в случае пластического потенциала, заданного произвольной изотропной выпуклой функцией, не зависящей от гидростатического давления). Все указанные решения построены для компактных (несжимаемых) сред.

Для некомпактных материалов механическое поведение и краевые задачи, описывающие процессы интенсивной пластической деформации, оказываются существенно сложнее; на сегодня известны только некоторые точные решения задач, в которых уплотнение материала происходит в том числе за счет эффектов дилатансии (прямая экструзия в осесимметричной и плоской постановке). Ранние работы по течениям пластически сжимаемых сред в каналах сосредоточены в основном на условии Мора–Кулона, ассоциированном с ним законе и гипотезе полной пластичности Хаара– Кармана (Cox [et al.], 1961 [5]). Ряд результатов получен методами верхней оценки и плоских сечений (Oh, Lee 1985 [6]). Из недавних результатов упомянем точные решения о нестационарном течении сферического слоя, подчиняющегося условию Мизеса–Шлейхера (Mon-chiet, Kondo, 2012 [7]), условию Друкера–Прагера или Мора–Кулона (Thore [et al.], 2009 [8]), эллиптическому условию типа Грина (Green, 1972 [9]) с постоянными коэффициентами (Shen [et al.], 2012 [10])). Указанные аналитические решения построены для двухконстантных моделей пластически сжимаемых сред, использование которых для описания поведения реальных материалов дает хорошие результаты в случае малых изменений плотности среды. Более сложные модели опираются на функциональные коэффициенты в уравнении поверхности текучести, явно зависящие от плотности. К числу таких относятся широко приме- няющаяся для моделирования вязкого разрушения модель Гурсона (Gurson, 1977 [11]), а также ряд моделей типа Грина, нашедших применение для описания прессования порошков и деформирования различных пористых тел. Поверхности текучести в обеих указанных моделях при нулевой пористости переходят в цилиндр Мизеса. Решение краевых задач в рамках моделей Гур-сона и Грина сопряжено с существенными сложностями. Для модели Гурсона известно приближенное аналитическое решение о движении среды в коническом канале без трения (Durban, Mear, 1991 [12]). Для модели Грина с непостоянными коэффициентами известные аналитические решения фактически исчерпываются двумя работами (Alexandrov [et al.], 2007 [13]; Alexandrov, Druyanov, 1990 [14]). В отличие от предыдущих, здесь полагается сухое трение по закону Кулона– Амонтона, а не трение Прандтля, используется приближенное уравнение равновесия, полученное по методу Хилла (Hill, 1963 [15]). В первой рассматривается обобщение условия Мизеса на некомпактные материалы, во второй – один из вариантов обобщения критерия Треска. Результаты последней демонстрируют, по всей видимости, нереалистичную податливость каркаса. Различным вариантам построения поверхностей текучести сжимаемых материалов с предельным переходом в призму Треска посвящена работа Revil-Baudard, Cazacu, 2014 [16].

Сравнительно недавно Сегалом [17] был предложен новый вид обработки материалов – боковая экструзия или равноканальное угловое прессование. Теоретических исследований, посвященных механике процесса, здесь существенно меньше. Упомянем работы [18–20], в которых речь идет о равноканальном прессовании пластически несжимаемых сред; ряд расчетных данных получен блочным методом, не имеющим очевидных преимуществ перед приближенным анализом в конечно-элементных пакетах, выполненном, например, в [21– 23]. Для некомпактных материалов (в том числе с дефектами в виде микропористости) известны только некоторые экспериментальные результаты и расчетные данные МКЭ-моделирования [24–26]. Последнее на сегодня является, по существу, единственным инструментом получения прогнозных оценок напряженно-деформированного состояния в процессах углового прессования сжимаемых сред.

Что касается фильтрационных процессов, вызванных деформированием пористой среды, то большая часть известных работ рассматривает каркас как вязкоупругий континуум [27–28] либо как вязкую жидкость [29]. Аналитические решения для таких процессов в рамках жесткопластического анализа до сих пор не получены, хотя во многих случаях необратимая деформация каркаса является основным механизмом, индуцирующим фильтрацию, а материал каркаса слабо проявляет вязкие свойства. В ряде исследований проведен учет пластической деформации каркаса [30] и получены результаты численного моделирования, например, в случае прессования в закрытой матрице [31].

В настоящей работе для жесткопластического анализа будем использовать эллиптическое условие текучести с постоянными коэффициентами как наиболее простое, позволяющее описать поведение сжимаемого материала в узком диапазоне изменения плотности. Для описания процесса фильтрации могут быть использованы два различных подхода. В связанной постановке поровое давление может оказывать влияние на переход материала из жесткого состояния в пластическое, в уравнении поверхности текучести будет присутствовать независимая скалярная функция внутрипорового давления. Последняя связана с параметрами деформированного состояния посредством уравнения фильтрации и баланса массы фаз. В этом случае векторное уравнение равновесия отличается от соответствующего для сухого каркаса наличием в правой части источника в виде градиента внутрипорового давления. Полную систему уравнений в этом случае можно представить в виде переопределенной системы автономных неоднородных квазилинейных ДУЧП первого порядка, совместность которой трудно прогнозировать. Второй подход, который и будет использован в настоящей работе, – использование несвязанной постановки. Такой вариант представляется неплохим приближением в случае достаточно высокой проницаемости каркаса. В этом случае поровое давление исключается из уравнения равновесия каркаса. Механическая часть задачи при ряде предположений кинематического характера сводится к интегрированию автономной системы двух квазилинейных ДУЧП первого порядка относительно одной неизвестной функции. Её решение используется для построения источника и коэффициентов эллиптического уравнения фильтрации жидкости. Это существенно упрощает постановку задачи, по сути дела сводя ее к известным уравнениям анизотропной теплопроводности.

• 1.    Постановка задачи, система уравнений процесса и модельные допущения

Рассмотрим процесс отжима жидкости из пористой среды при прохождении ее через зону сопряжения двух плоских щелевых каналов одинакового сечения (рисунок). Сток организован на цилиндрической поверхности r = r. Будем полагать, что на входе и на выходе из деформационной зоны не происходит разрыва скоростей. Следуя принципам жесткопластического анализа, считаем, что деформирование пористого каркаса исключительно необратимо и происходит в секторе кольца D = [ГрГ ]х[0,Фо]. Отсчет угловой координаты начинается с поверхности выхода из деформационной зоны и направлен против движения материала. На выходе из области деформирования пористый материал с остатка- ми флюида удаляется, так что давление в жидкости на поверхности ф = 0 не отличается от атмосферного.

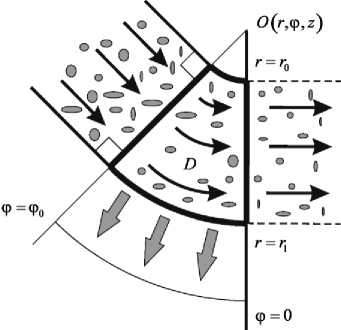
Рис. 1. Схема процесса отжима поропласта

Fig. 1. Diagram of the poro-plastic materials pressing

Для пористого материала примем пластический потенциал вида

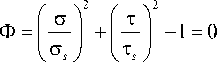
где    ct_s , т - константы,   3 с = tr ( о ) ,    2 т ² =

= tr ( о ² ) - tr ( о ) 2 / 3; о — тензор макроскопических напряжений Коши в каркасе; а также ассоциированный с потенциалом (1) закон пластического течения

. д Ф

Е = Л , д о

где Л - скалярный пластический множитель; ε – тензор скорости деформации каркаса,

2 е = ( V® v ) T + ( V® v ) ; V - оператор Гамильтона; v – вектор скорости материальных точек каркаса.

Уравнения (1) и (2) позволяют установить связь между тензором напряжений и тензором скорости деформации:

22 о      Е + 9 1 tr ( е )      _а_ 1 ^ст s У  1

2 ^ " у tr ( е ² ) + 9 tr ( е ) 2 ,    = 2 1^)   ³ .

Будем пренебрегать массовыми и инерционными силами. Равновесная конфигурация должна удовлетворять уравнению

• V- о = 0 .

  
  

Безразмерная плотность каркаса р удовлетворяет уравнению неразрывности dp + V-(pv ) = 0.                 (5)

Введем вектор скорости фильтрации vf таким образом, что полная скорость движения частиц жидкости равна (v + vf). Принимая для обоих компонентов смеси (материал каркаса и флюид) условие несжимаемости, аналогично (5) запишем для флюида уравнение

^^^'Ц ¹ -Р ) ( ^{v + v}f )] = 0.       (6)

Суммируя (5) и (6), имеем [32]

V-[ v + ( 1-р ) v f ] = 0.                (7)

Будем рассматривать достаточно медленное потенциальное течение ньютоновской жидкости в каркасе, подчиняющееся линейному закону фильтрации Дарси

,         , , к.

q _в( 1 -р ) v f =--V P .             (8)

Ц

Здесь q – вектор потока, прямо пропорциональный проницаемости k и обратно пропорциональный вязкости флюида ц ; P - внутрипоровое давление. В рассматриваемом процессе коэффициент вязкости можно считать постоянным. Проницаемость среды можно считать постоянной лишь в самом грубом приближении. В общем случае k есть функция относительной плотности каркаса, например, заданная соотношением Козени– Кармана. Упомянутое соотношение существенно нелинейно; небольшой рост относительной плотности каркаса может вызвать заметное падение проницаемости.

Уравнение (4) с учетом (3) интегрируется относительно вектора скорости точек каркаса. Уравнение (5) тогда позволяет найти распределение плотности, а уравнения (7) и (8) служат для определения скорости фильтрации и внутрипорового давления.

Введем цилиндрическую систему координат (см. рисунок) и далее будем полагать, что

• 1)    процесс стационарный, др / 5 1 = 0,

• 2)    движение точек пористого каркаса происходит по дугам окружности, единственная ненулевая компонента вектора скорости есть г_ф = r to ( r , ф ) < 0, m - угловая скорость; 5m / 5ф <  0, течение замедляется.

Краевые условия:

– на выходе из деформационной зоны канала отсутствует противодавление ст I =0;(9)

фф|ф=0      ;(

– известна линейная скорость материала на входе в деформационную зону канала v     =- v = const;

ф ф=ф0

– известна относительная плотность на входе в деформационную зону канала pl    = p„ = const;

¹ ф=ф 0       ⁰

—

^ + 2 „ ,,

д x

– азимутальная составляющая вектора скорости фильтрации на входе в деформационную зону канала равна нулю v f = 0 или, с учетом (8);

^Ф !ф=Ф о

дф

= 0,  '°+( дx х

° гг

—

\ д° гф о +--- фф) дф

= 0

образуют переопределенную систему относительно

V ( x , ф ) :

д P

дф

Ф=Ф о

= 0;

cos _V[ 1 ^{— (— 2 —} 2 ) tan ² ф]^ = 0, ^

cos тдН*2—2) tan v*+2

= 0.

– на выходе из деформационной зоны канала внут-рипоровое давление равно нулю

P _п= 0;                     (13)

Iф=0                                           v 7

- на цилиндрической поверхности г = г„ задано условие непротекания vf\   = 0 или, с учетом (8),

I г = г ₀

Система (18) совместна, из первого уравнения следует Sv / д x = 0, т.е. напряженное состояние не зависит от радиальной координаты. Второе уравнение (18) имеет решение

V = — 2 х^— 1 ( ф+ C ) ,

д P д г

= 0;

где C = — — — - константа интегрирования, определяющаяся краевым условием (9).

Учитывая (17), tan V = — ^— 1 ( дю / д x )( дго / дф ) 1 , откуда

- цилиндрическая поверхность г = г проницаема для жидкости

P_r_г = 0.                      (15)

I ^г = ^г 1

2. Решение механической части задачи

С учетом сделанных предположений о кинематике материальных точек каркаса тензор скорости деформации имеет вид

е = ^ e ^ e —J_£^(e ® e + e ® e ^,     (16)

дф ^{ф ф} 2 д x ^{( r ф ф r} )

введена замена независимой переменной x = ln ( г_х / г ) .

Соотношение (3) с учетом (16) позволяет получить компоненты тензора напряжений в виде

° гг = ° _zz    ^т , ( — ^{— 2} Х ^{- 1} ) ^cos V ,

° фф    ^т , X ^cos V , ° г ф    ^т , ^sin V ,

sin V =

F'

Q

, cos v =

+х ²

_^х , V^2 +х ²

o^f ^ 0, х=V20+» ) . д x (дф)          ’

Напряженное состояние каркаса определяется одной функцией v ( x , ф ) • Из (17) следует, что при отсутствии противодавления на выходе из канала реализуется состояние чистого сдвига.

С учетом (17) две нетривиальные компоненты уравнения равновесия (4)

-—X ^cot ( ² — ^{— 1} ф)т~ = ⁰ .            ⁽¹⁹⁾

д x       ^х      ’ дф

Линейное уравнение в частных производных первого порядка (19) интегрируется методом характеристик [33] и позволяет получить в замкнутом виде угловую скорость ю = F(Е), Е = x — lncos1/2 (2—1ф),      (20)

где F – произвольная функция своего аргумента.

Теперь приведем полученное общее решение (20) в соответствие с краевыми условиями процесса. Компонента    вектора    скорости    точек    каркаса уф = ге—xю = ге—xF ^x — lncos1/2 (2——1ф)^ на входе в канал не зависит от x . Это возможно только в том случае, если F(е) = F0еЕ, где F - константа, определяющаяся краевым условием (10). Таким образом, кинематика среды описывается уравнением cos1/2 (2—1ф0)

v ф = ^— v 0---- _1/2V       , ф е [ 0, ф 0^] ,        ⁽²¹⁾

cos ( 2 — ф )

а необходимое давление для поддержания стационарно го течения имеет выражение |°фф| = —Т sin(2——1ф0) ■

Из условия стационарности (5) и краевого условия (11) следует

p ^v ф = ^—Р 0 v 0 ■                     ⁽²²⁾

Распределение плотности устанавливается исходя из (22) с учетом решения (21).

3. Решение задачи фильтрации

Соотношения (7) и (8) позволяют записать квазилинейное эллиптическое уравнение для скалярного поля внутрипорового давления:

co

W (х, ф) = £ n =0

g n sin ( ^X n ф ) ^X n ^ch ( ^X п ^х 0 )

X

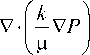
= V- v .

^X[ e ^- * ⁰ sh ( X п ^х ) ^-X n ch ( X n ( ^х 0 ^{- х} ) ) ] ,

Правая часть (23) согласно решению (21) есть известная функция пространственных переменных, V- v = r ^-1 (d v _ф / дф ) . Коэффициент фильтрации к / ц считается известной функцией относительной плотности каркаса. Согласно (21), (22) величина к / ц может быть записана как функция пространственной переменной ф .

n(2 n +1)           2 'r ,  .     / x

^X n =    ----~ , g n = — J ^f ( ф ) sin ( ^X n ф ) ^d ф.

2ф 0           ф 0 0

Согласно (8) поток флюида из деформационной зоны через поверхность r = r определяется выражением

^{( 1 -}р ) ^vfL

_г д w

"^{f +}Т"

^{д х} х = 0

3.1. Случай постоянной проницаемости

Если коэффициент к / ц не зависит от локальной относительной плотности каркаса (а следовательно, и от пространственных координат), то (23) представляет собой уравнение Пуассона

Максимальное значение потока достигается при х0 ^ o, т.е. в канале с особенностью r = 0

o max { (1 -p) vrf|r_r } = - f + ZXngn sin (Xnф), 1                 n=0

д ( дP)  д2 P   ц Svф r — I r— 1 +--- = r--- .

д r V д r )  дф     к дф

соответствующая интегральная мощность потока через поверхность r = r

Введем, как и прежде, замену независимой пере менной х = ln (r / r), обозначим х0 = ln (r / r). Также

ф 0                               ф 0             o

J ( 1 ^-p ) v fL. d ф=^- / ^fd ф⁺ Е g n .

0                      ^Г1              0               n =0

введем     замену     зависимой     переменной

P = r ( ц / к ) [ W ( х , ф ) + e ^{- x}f ( ф ) ] . Здесь функция f ( ф ) удовлетворяет обыкновенному дифференциальному уравнению f" + f = S v / дф с краевыми условиями

При r = 0 мощность стока, как и мощность работы внешних сил, линейно зависит от толщины щелевого канала r .

f ( 0 ) = 0 и f ' ( ф ₀ ) = 0:

^{f (}ф ) =

cos

ф ф| хф cos ф dф + sin

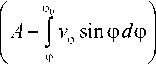
A = v ₀ cos

ф 0

ф₀ + tan ф₀ J т _ф cos ф d ф .

Тем самым краевая задача для уравнения Пуассона (24) в секторе кольца с условиями (12)–(15) сводится к краевой задаче для уравнения Лапласа в прямоугольнике

д ² W д ² W

—т +--т дх2   дф2

3.2. Общий случай проницаемости

Пусть коэффициент фильтрации к / ц представляет собой произвольную гладкую монотонную функцию относительной плотности (и в силу (21), (22) пространственной переменной ф ). В этом случае для уравнения (23) неизвестны даже частные точные решения. Далее сведем (23) к уравнению анизотропной теплопроводности с частным случаем анизотропии, для которого такие решения известны [33].

Введем новые независимые переменные r       г к х = ln—, 0=f — dф,              (28)

^r      0 ц

с условиями

Ч = 0 =- f ( v ) , W .=0 = 0 ^,

д W д х

= e ^{- х 0} f ( ф )

д W

обозначим 0 = Г^Ф ° ( к / ц ) d ф. Для преобразования (28) 0

существует обратное ф(0) = Inv[0(ф)], соответствен но, к / ц и уф могут быть записаны как функции 0.

Тогда (23) примет вид

Точное решение задачи (24)–(25) известно [33]:

д ² P   д ( к ) д P       _х S v _ф

—г + — _ — = re --- дх2   д0 (ц) д0 1 д0

Заменяя в (29) зависимую переменную P = г W ( X , e ) + e ^{- x}f ' ( e ) ], где f ( e ) удовлетворяет линейному уравнению ( k / p ) 2 f + f = у_ф с граничными условиями f (6₀) = - ^v o и f ' ( 0 ) = 0 , имеем смешанную краевую задачу

52 W 5 ( k Y 5 W

+ I I 5 x ²    56 (pj 56

W x = 0 =- f '(⁶) ^, W 6= 0 = ⁰ .

5 W

5 x

= e~x0 f '(e). ^W v '   56

= 0.

Заключение

В рамках жесткопластического анализа получено точное аналитическое решение задачи о стационарном течении полосы из некомпактного материала через сопряжение плоских каналов в зоне интенсивной пластической деформации. Определены компоненты тензора напряжений Коши, тензора скорости деформации и распределение относительной плотности материала. Получены