Финансовая реализуемость инновационных проектов в игровой постановке

Как бы ни был общественно привлекателен инновационный проект, если не удается решить проблему его финансового обеспечения, то проект обречен на неудачу. Финансовой реализуемости различных инвестиционных проектов в рыночных условиях уделяется большое внимание в современной экономической теории и ее приложениях [1 -- 3] и др.

Однако анализ финансовой реализуемости проводится, как правило, при фиксированных параметрах самого проекта, определяющих потребные финансовые потоки. Вместе с тем понятно, что особенности финансового обеспечения могут оказать влияние на результаты оптимизации исходных параметров проекта. Так, если у инициатора проекта новой технической системы не хватает собственных средств для компенсации первичных расходов в ожидании будущих доходов и ему не удалось привлечь достаточно кредитоспособных соинвесторов, то, чтобы вообще не отказаться от проекта, инициатор может пойти на снижение выбранного им ранее уровня инженерного совершенства системы. За счет этого ему удастся сократить затраты на проектирование и производство, несколько поступившись, конечно, будущими доходами от эксплуатации менее совершенной системы.

Высказанные соображения свидетельствуют в пользу совместного рассмотрения проблем инженерного проектирования и финансового обеспечения инноваций, чему и посвящена предлагаемая статья.

Статья продолжает предшествующие работы авторов [4, 5] о проектировании, производстве и эксплуатации многоцелевых технических систем. Там тоже присутствовали финансовые показатели, но только при формировании целевой функции — итоговой прибыли. Проблема финансовой реализуемости проекта посредством соинвестирования и кредитования не затрагивались, а лишь упоминались. Основное внимание было уделено неопределенным факторам и постепенному уточнению информации о них при поэтапном принятии управленческих решений. Однако сейчас для облегчения математических конструкций вопросы неопределенностей временно оставлены в стороне.

• II.    Участники финансирования инновационного проекта и их управляющие воздействия

Все множество лиц и организаций, принимающих участие в финансировании инвестиционного проекта, разделим, отвлекаясь от деталей, на две категории — на соинвесторов и кредиторов.

Соинвесторы финансируют проект, получая после его реализации и расплаты с кредиторами долю итоговой прибыли, пропорциональную вложенным каждым из них средствам.

Участие соинвестора в реализации проекта может заключаться не только во вложении денежных средств, а, например, в предоставлении оборудования, производственных площадей, объектов интеллектуальной собственности (само научно-техническое новшество) и т.д. В конечном итоге неденежное участие в проекте может быть пересчитано в денежные средства. К соинве-сторам отнесем также патентодержателя (изобретателя) научно-технического новшества. Доля патентодержателя в будущих доходах исчисляется пропорционально стоимости патента и возможных дополнительных его финансовых вложений в проект. Все условия графика вложений соинвесторами и получения доходов от проекта оговариваются в инвестиционном контракте, в котором также предусматриваются санкции за нарушение графика платежей инвесторами.

Кредиторы привлекаются соинвесторами к участию в финансировании проекта в случаях нехватки у соинвесторов собственных средств. Существенное отличие кредиторов от соинвесторов состоит в том, что договор кредитования оговаривает правило возврата временно одолженных средств вне прямой зависимости от будущих доходов соинвесторов.

Формы кредитования могут быть различными [1--3]. Но всегда соинвесторы ориентированы на долевое участие в прибыли, поэтому каждый из них заинтересован в максимальной суммарной прибыли. Для целей настоящего рассмотрения все соинвесторы могут в рамках необременительных дополнительных условий считаться единым участником, распоряжающимся объединенными финансовыми ресурсами для обеспечения реализации проекта. Соинвесторы также осуществляют подбор кредиторов и все расчеты с ними, распоряжаясь всеми доходами от проекта. Объединенные соинвесторы будут называться еще основным участником проекта, который в последующей схеме и формулах помечается индексом e = 0.

Кредиторы, именуемые еще привлеченными участниками e ∈ E , остаются персонифицированными, поскольку договоры с ними индивидуальны и, как правило, априори несравнимы из-за разноаспектности их характеристик, таких как объем и динамика кредитования, проценты за кредит, срок и динамика погашения долга.

Кредитор заинтересован в неукоснительном соблюдении договора с соинвесторами, обеспечивающего ему желаемый уровень доходности. Техника заключения договоров не рассматривается. Все множество E потенциальных договоров считается сформированным заранее, а соинвесторы могут выбирать из него подходящие. Возможны случаи, когда кредитор является одновременно и соинвестром. И тогда он представляется в виде двух различных участников, имеющих свои интересы и управления.

Связи между проектом и участниками его финансирования показаны на рис. 1. Связи формализованы в виде ориентированных финансовых потоков, характеризуемых переменной интенсивностью в непрерывном времени t (для определенности р ./ год) на протяжении всей продолжительности [0 ,T ] жизненного цикла проекта:

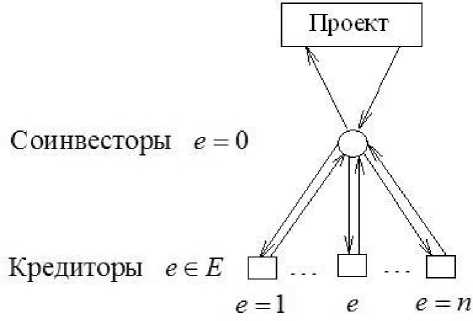
Рис. 1. Схема связей между участниками финансирования проекта

u — расходы соинвесторов на проектирование, испытания и производство новой технической системы, то есть непосредственно на реализацию проекта, называемые далее первичными расходами;

v — доходы соинвесторов от эксплуатации системы, называемые первичными доходами .

Остальные потоки, называемые вторичными , связывают соинвесторов с кредиторами для обеспечения финансовой реализуемости проекта при временной нехватке у соинвесторов собственных средств:

• v _e — поток заемных средств от e -го кредитора соинвесторам;

u e — поток средств, возвращаемых соинвесторами e -му кредитору (выплаты долгов и процентов).

С позиции соинвесторов v _e — это вторичные доходы, а u _e — вторичные расходы.

Горизонтальные финансовые связи между кредиторами по делам, относящимся к проекту, не предусмотрены (хотя связи между кредиторами возможны по другим, не рассматриваемым здесь, операциям).

Перечисленными финансовыми потоками распоряжаются разные участники, отслеживая свои интересы, соблюдая инженерно-технические ограничения и выполняя принятые на себя обязательства.

Соинвесторы управляют первичными расходами u и потоками u e расплат с кредиторами e ∈ E . Множество кредиторов E подбирается также соинвесторами по результатам переговоров с потенциальными кредиторами, где согласуются правила кредитования и расплаты с долгами. Ориентируясь на эти правила, на собственные финансовые возможности и на потребные первичные расходы, соинвесторы выбирают еще желательную для них верхнюю границу v e потока заемных средств v _e , определяемого окончательно e -м кредитором.

Воздействие соинвесторов на первичные расходы по проекту реализуется апосредованно — через выбор инженерно-технических параметров проектируемой системы и масштабов ее производства, что достаточно подробно разбиралось в [4, 5] с учетом возможных неопределенностей. Сейчас, не прибегая к такой детализации, будем считать, что соинвесторы распоряжаются непосредственно первичными расходами u как независимым управлением в пределах известного им множества U гарантированной допустимости:

u Е U = fix.

Множество U отражает все инженерно-технические особенности проектируемой системы. Соблюдение условия (1) обеспечиывает материальную (но еще не финансовую) допустимость первичных расходов при любых реализациях неопределенных факторов в прогнозируемых пределах, что подчеркивается названием «множество гарантированной допустимости». В формировании множества U финансовые ограничения не участвуют — они будут построены особо. По этой причине вторичные финансовые потоки на само множество U не влияют, но они скажутся на результатах оптимального выбора управления из этого множества при соблюдении условий финансовой реализуемости проекта.

Будем считать также построенным соответствие D между первичными доходами и расходами. Это соответствие по функции и Е U однозначно определяет верхнюю границу v доходов от реализации проекта. Соинвесторы по договоренности между собой могут отложить часть полученных доходов на будущую совместную экономическую деятельность или благотворительность. Так что у них есть ограниченная сверху возможность управления потоком v первичных доходов, используемых для расплаты с кредиторами и выплаты девидентов:

0 6 v 6 v = D ( u ) .

Отображение D определяется соответствием между инженерно-техническими характеристиками проекта, с одной стороны, и первичными расходами u и максимально возможными первичными доходами v — с другой. После исключения отсюда инженерно-технических характеристик и получается отображение D : и ^ v .

Это отображение известно инвесторам. Оно не реагирует на вторичные финансовые потоки, а более, пока никак не конкретизуется. При наличии неопределенностей под v в (2) понимается гарантированная оценка первичных доходов. В ограничении (2) можно явно выделить резерв на упомяную выше «прочую» деятельность соинвесторов, но можно этого и не делать, считая ограничивающую функцию v уже уменьшенной на величину такого резерва.

Помимо управления первичными финансовыми потоками u и v у соинвесторов есть возможность воздействия и на вторичные финансовые потоки u e ,v e , связывающие соинвесторов e = 0 с кредиторами e ∈ E , как было показано на рис. 1.

Отношения соинвесторов с кредиторами регламентируются договором о кредитовании, который формализуется в виде отображения De , однозначно определяющего по программе заемных средств ve программу погашения долга с процентами. В договоре De могли бы быть предусмотрены некоторые свободы для соинвесторов, разрешающие им, например, досрочную расплату с долгом. В качестве символа подобных свобод, не ущемлящих интересов кредиторов и не противоречащих предположению об однозначности соответствия De , будем считать, что соинвесторы могут сами выбирать программу ue расплаты с долгом, нигде не опускаясь ниже функции ue , однозначно вычисляемой по договору De в ответ на программу займа ve :

U e >  u _e = D e ( v e ) , e G E,                                    (3)

где отображение D _e известно и соинвесторам, и e -му кредитору и недоступно односторонним изменениям.

Соинвесторы могут влиять также на программу заимствований v _e , высказывая кредиторам свои пожелания в виде верхней границы заимствований V e .

Кредиторы имеют право отступать вниз от этой границы при назначении ими фактических потоков кредитования v _e , не превышающих собственных финансовых возможностей V _e :

V e 6 min { V e ; V e } , e G E.                                      (4)

В заключение настоящего раздела приводится перечень управлений, которые будут выбираться участниками проекта при решении своих задач, формируемых в последующих разделах.

Соинвесторы ( e = 0) выбирают:

u — первичные расходы из множества (1) гарнтированной инженерно-технической допустимости, v — первичные доходы, ограниченные сверху инженерно-техническими возможностяими (2), ue — выплаты кредиторам, ограниченные снизу долговыми обязательствами (3),

V — верхнюю границу желательных заимствований.

Кредиторы ( e ∈ E ) выбирают:

v e — фактическую программу кредитования, ограниченную сверху в (4) желаниями соинвесторов V e и своими финансовыми возможностями V e .

При этом фигурирующие в ограничениях (1) — (4) множество U , отображения D ( u ) и D e (v e ), а также функция V _e считаются уже сформированными и известными всем участникам.

• III.    Условия финансовой реализуемости проекта и функции полезности его участников

Финансовые потоки столь же реальны, что и материальные, и играют не меньшую роль в условиях допустимости управлений. Все материальные, инженерно-технические ограничения были лаконично представлены условиями (1), (2). Условия (3), (4) открывают список финансовых ограничений, который продолжается ниже.

Прежде всего предстоит обеспечить выполнение закона сохранения финансовых потоков. Этот закон здесь записывается в непрерывном времени t в виде интегральных уравнений динамики специализированных инвестиционных счетов каждого из участников проекта. Под инвестиционным счетом S _e (t) е -го участника понимаются нарастающие итоги его финансовой деятельности по проекту, представляемые с учетом начального состояния счета S _e (0) интегралом по отрезку [0 ,t ] от разности (сальдо) интенсивностей потоков всех его доходов и всех расходов, включая их возможные δ -всплески:

для соинвесторов ( е = 0; v и v e — доходы, и и u e — расходы):

S o ( t ) = S o (O) + Z

t

^{v ( t} ) ⁺ ZLv e ^(T )

e ∈ E

dτ -

u ( t ) + ^X и_е(т ) dT >  0 17

V t G [0 ,T ] ,

e ∈ E

для кредиторов ( e ∈ E ; u _e — доход, v _e — расход):

t

t

S _e ( t ) = | u e (T)dT — | v e (T)dT >  —m e (t) V t G [0 ,T ] .

Соинвесторы на своем счету располагают начальной суммой S o (0) >  0, которая полагается в (5) фиксированной. Ни в один из моментов времени t на отрезке [0 ,T ] жизненного цикла проекта их текущий счет не должен стать отрицательным.

Счет S e ( t ), который ведет e -й кредитор по своим финансовым взаимодействиям с соинвето-рами, начинается с нуля: S _e (0) = 0. Кредитор может временно позволить себе иметь на этом счету отрицательный нарастающий итог, ограниченный снизу некоторым уровнем ( - m e ), который он устанавливает по прогнозам операций с другими заемщиками. Окончательный результат, естественно, должен быть положительным.

Типичный вариант поведения функций (5, 6) показан на рис. 2, 3, 4, 5. Он соответствует трем кусочно-постоянным и одному импульсному финансовым потокам, заданным рис. 2, 3. Первоначальные расходы по проекту u(t) сосредоточены на полуинтервале [0 ,t * ), где их интенсивность принята постоянной положительной, а вне этого полуинтервала — нулевой. В момент времени t _∗ расходы сменяются доходами v ( t ), прежде нулевыми. Интенсивность потока доходов на полуинтервале (t * ,T ) тоже полагается постоянной положительной (рис. 2).

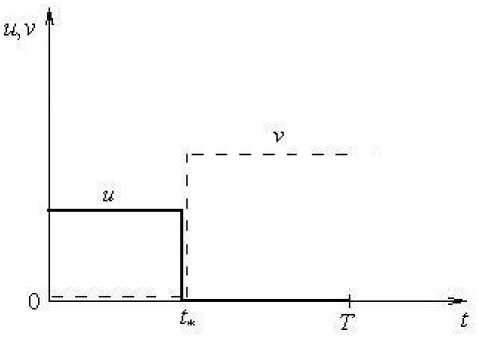
Рис. 2. Иллюстративный пример первичных финансовых потоков u, v

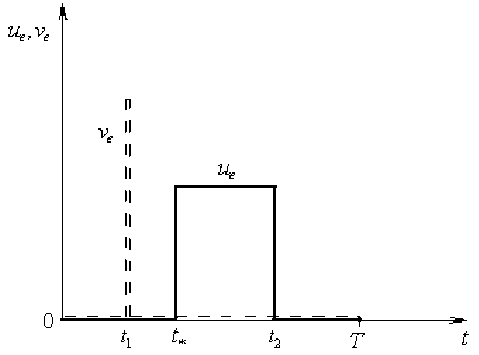
Рис. 3. Иллюстративный пример вторичных финансовых потоков u _e , v _e

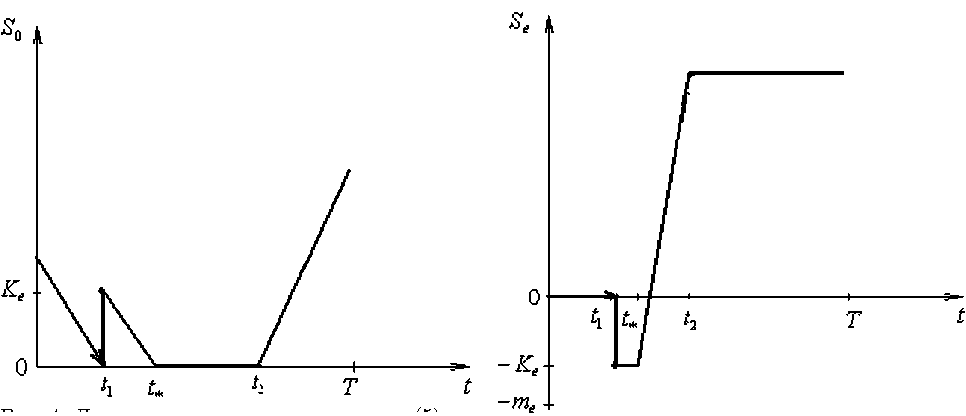
Рис. 4. Динамика инвестиционных счетов (5) со-инвесторов S 0 , соответствующая рис. 2, 3

Рис. 5. Динамика инвестиционных счетов (6) со-инвесторов S _e , соответствующая рис. 2, 3

До начала поступления доходов от проекта, в момент t 1 , заканчиваются собственные средства соинвесторов: S o ( t i ) = 0 , 0 < t i < t * , и тогда они мгновенно берут конечную сумму кредита K e у единственного кредитора e , т.е. интенсивность потока кредитования выбрана в виде обобщенной 5 -функции: v _e ( t ) = K e 5(t — t i ). В договоре с кредитором оговорено, что соинвесторы начнут выплачивать долг с процентами, когда у них появятся первичные доходы от проекта (как пример). Выплаты должны производиться равномерно и закончиться в установленный момент времени t 2 < T (рис. 4. 5).

Текущие ограничения снизу в (5, 6) на состояния инвестиционных счетов участников еще не исчерпывают всех условий финансовой реализуемости проекта. Каждый из участников, будучи свободным в своем выборе, должен быть уверен в достаточном уровне прибыльности конечных итогов своей инвестиционной деятельности.

Эффективность инвестиций оценивается различными показателями, исчерпывающе представленными и проанализированными в [1--3]. В настоящей статье используется два распространенных достаточно естественных показателя.

С одной стороны, участники отслеживают прибыльность каждой единицы своих вложений в проект (относительный, удельный показатель). С другой стороны, они хотят увеличить сумму полученной прибыли (абсолютный, объемный показатель). Такие показатели не заменяют друг друга. Например, удельная прибыльность инвестиций может быть высокой, а масштаб проекта небольшим, и тогда проект будет не привлекателен для крупного инвестора. Или, наоборот, проект крупномасштабный и сулит большую сумму прибыли, но удельная прибыльность инвестиций в него невелика, например меньше, чем процент по депозиту в банке, и тогда проект снова оказывается непривлекательным.

При расчете показателей эффективности долговременных инвестиций, типичных для инновационных проектов, участники более ценят «сегодняшние деньги», чем ту же сумму денег в будущем, что привычно формализуется в виде убывающих по времени дисконтирующих множителей при подсчете нарастающих итогов затрат и доходов. Это — модель психологической характеристики участников любой экономической деятельности. Однако в бухгалтерских расчетах типа (5, 6) дисконтирующие множители не используются.

Первый из упомянутых выше показателей эффективности инвестиций называется индексом доходности и определяется в [1 -- 3] как отношение кумулятивного дисконтированного дохода, приходящегося на долю участника проекта, к дисконтированному кумулятивному расходу. Этот показатель используется в настоящей статье как дополнительное финансовое ограничение: индекс доходности для каждого участника проекта должен оказаться не ниже некоторого фиксированного уровня I e >  1, начиная с которого деятельность в проекте считается им приемлемой.

Ограничения по доходности удобно представить в виде, линейном относительно управлений v, v e , u, u e :

для соинвесторов ( е = 0) —

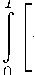
T e-λ0tdt,

e ^{-λ 0 t} dt >  I 0

для кредиторов ( е G E ) —

jue(t)e Xetdt > Ie 0

jve(t)e Xetdt, 0

где A o , A e = fix >  A > 0 — нормы дисконтирования ценности денег, устанавливаемые для себя каждым участником на уровне не ниже банковского процента λ .

В экономической литературе более распространена другая, эквивалентная, запись дисконтирующей функции [1]:

(1 + E)-т вместо e-Xt, где E — годовая безразмерная норма дисконтирования, λ — мгновенная размерная норма, т = t(1 год )-1 — безразмерное время, t — размерное время, измеряемое в годах.

A = [ln(1 + E )](1 год ) ^{- 1} ~ E (1 год ) ^{- 1} при E ^ 1 (обычно E ~ 10 ^{- 2} ).

Второй показатель эффективности — так называемый чистый дисконтированный доход , здесь используется в виде функций полезности участников проекта, стремящихся к увеличению значений каждый своей функции:

для соинвесторов e = 0 —

T

F0

^{v(t) +} 52 v e ^(t)

e ∈ E

- ^u(t) - 52u e ^(t)

e ∈ E

e -^ 0^tdt ~ max ,

для кредиторов ( e G E ) —

F e

T

= j[u e ^(t)

— v e ( t )] e ^{X e t} dt ~ max .

Символическая запись F ~ max в (9, 10) не означает классическую задачу максимизации, а лишь указывает на желательность увеличения значений функции F . Несовпадение друг с другом функций полезности (9, 10) и относительная независимость действий участников проекта приводит к необходимости игровой формализации, что и будет сделано в следующем разделе.

• IV.    Игровое равновесие

Как уже отмечалось, интересы участников финансирования инновационного проекта, моделируемые функциями полезности (9, 10), различны. Каждый из участников может индивидуально распорядиться своим набором управлений в рамках условий допустимости. Управления одного участника воздействуют на свою и чужие функции полезности (9, 10), а также на условия допустимости (3) — (7, 8) чужих управлений. Все это — признаки, указывающие на игровой характер взаимодействия участников проекта.

Игра моделирует предварительный этап переговоров, когда потенциальные участники решают для себя вопрос, финансировать проект или нет. Игра формализуется как одношаговая: все участники одновременно выбирают свои управления в виде функций времени сразу на весь отрезок жизни проекта, не зная чужих выборов. Однако все функции полезности и все условия допустимости управлений, свои и чужие, считаются заранее известными всем потенциальным участникам.

Специфика игры о финансировании инновационного проекта состоит в том, что управления участников воздействуют не только на функции полезности, свои и чужие, но и на условия допустимости чужих управлений. В таких случаях говорят об играх с запрещенными ситуациями [6], более точно называемыми еще играми со связанными ограничениями [7], а лучше — со связывающими ограничениями, поскольку они связывают возможные выборы разных участников друг с другом.

Ниже для каждого e -го участника проекта приводится сводка сведений из п. 2, 3, требуемых в нормальной форме описания игр: функция полезности F e , управления x e и множество их допустимости X _e . При этом специфические обозначения управлений, перечисленные в конце п. 2, для сокращения записей заменены на унифицированные.

Для соинвесторов ( e = 0) обозначим эти формулы (11):

F o ( x _e ; x e ) ~ max

— функция полезности (9),

X o = ( u, v ; U e , V e , e G E ) ,                                          (11)

— свои управления,

X o ( x E ) = { x o :      удовлетворяют условиям (1)--(3) , (5) , (7) }

— множество допустимости,

X E = ( V e , e G E )

— чужие управления, воздействующие на F 0 и X 0 .

Для кредиторов ( e € E ), обозначим эти формулы (12):

F _e ( x _e ; x o ) ~ max

— функция полезности (10),

X e = V e ,                                                (12)

— свои управления,

X _e ( x o ) = {x _e :      удовлетворяют условиям (4) , (5) , (7) }

— множество допустимости, x0— чужие управления, воздействующие на Fe и Xe .

Здесь ответственность за выполнение разных ограничений в соответствии с их смыслом поделена между участниками, что было предложено отслеживать в [7]. За соблюдение каждого из ограничений, наложенных на управления, отвечает хотя бы один участник игры, управление которого фигурирует в этом ограничении, так что за ограничения только с чужими управлениями участник не отвечает. За ограничения, куда входят управления сразу нескольких участников, могут отвечать каждый из них или только некоторые.

По этим правилам и были сформированы в (11, 12) множества X o ( x e ) и X _e ( x o ), которые уместно называть множествами индивидуальной допустимости управлений.

Из-за наличия в игре связывающих ограничений эти множества зависят от чужих выборов. И возможна ситуация, когда индивидуально допустимый выбор одного участника не оставляет ни одного индивидуально допустимого выбора для другого. Такая ситуация означает кризис идеи индивидуального принятия решения и заставляет внести в игру элемент коллективизма.

Во избежании возможной недопустимости управлений в играх со связывающими ограничениями все участники помимо выполнения условия индивидуальной допустимости должны принять дополнительное обязательство по обеспечению совокупной допустимости управлений [8, 9].

Если всем участникам финансирования проекта удалось соблюсти свои условия индивидуальной допустимости из (11, 12), то это и означает выполнение соглашения о совокупной допустимости.

Условие совокупной допустимости удобно записать, используя составной вектор всех управляющих функций:

x = ( x o , x i , ..., x n ) ,       где       { 1 , ..., n} = E.                           (13)

Составной вектор (13) должен удовлетворять всем условиям, наложенным на управления, что записывается в виде требования его принадлежности множеству X совокупной допустимости, определяемому через множества индивидуальной допустимости:

x € X = {x : x o € X o ( x o , ..., x n ) , x i € X i ( x o ) , -., x n € X n ( x o ) } .                (14)

Все совокупно допустимые выборы согласно определению (14) индивидуально допустимы. Если множества индивидуальной допустимости не зависят от чужих управлений, как в классических задачах на прямых произведениях недеформируемых множеств индивидуальной допустимости, то верно и обратное. Но в играх со связывающими ограничениями типа (11, 12) соблюдение одним участником только своих ограничений, если он делает выбор первым, не всегда оставляет непустым множество индивидуальной допустимости для другого участника, делающего свой выбор вторым, что означает тогда нарушение условия (10) совокупной допустимости управлений.

Конструктивная запись условия (14) совокупной допустимости в рассматриваемой игре о финансировании инновационного проекта будет представлена ниже для двух вариантов рациональных решений: для равновесных решений по Нэшу и для кооперативных решений.

Идея равновесия по Нэшу привлекательна для экономически мотивированных индивидуумов, стремящихся к самостоятельности в принятии решений. Решения всеми участниками игры принимаются одновременно без знания конкретных выборов окружающих, но с твердой уверенностью, что окружающие будут придерживаться равновесия, то есть реализуют свои компоненты совокупного равновесного вектора управлений (13). Задача состоит в том, чтобы отыскать такой вектор x°, который, во-первых, был бы совокупно и индивидуально допустим, и, во-вторых, чтобы ни одному из участников было бы невыгодно в смысле своей функции полезности отклоняться по-одиночке от этого вектора при условии, что остальные его придерживаются.

Все сказанное, как известно из теории игр, означает для каждого участника игры, что в равновесии x ° он достигает максимума своей функции полезности по своим управлениям при фиксированных на равновесных уровнях управления остальных участников:

для соинвесторов ( е = 0):

x G X g ( x E ): F o ( x 0 ; x E )=   max   F g (x g ; x E ) = W",      где      X g ( x E ) = { x g : ( x g ,x E ) G X } ;

x o GX o ( x E )

для кредиторов ( e G E ):

x o G X e ( x o ): F e ( x o ; x o )= max F e ( x e ; x o ) = W o , X e GX e ( x O )

где

X e ( x o ) = { x e : ( x o ,x _e ,x e ) G X } ,x _e = ( x o o ,e G E \{ e } ) .                     (16)

От классического определения нэшевского равновесия, пригодного для игр на прямых произведениях недеформируемых множеств индивидуальной допустимости, обобщенный вариант (15, 16) из [9] для игр со связывающими ограничениями отличается специальной конструкцией множеств X g и X e , на которых отыскиваются максимумы в (15) и в (16). Элементы этих множеств для участника, анализирующего свои мыслимые отклонения от равновесия, должны удовлетворять условию (14) совокупной допустимости составного вектора (13), где на месте управления выделенного участника стоит отклоняющийся аргумент (без верхнего значка «градус»), а на всех остальных местах — равновесные аргументы, помеченные верхним значком «градус».

В соответствии со сказанным подробная расшифровка лаконичных определений множеств X g и X _e , приведенных в (15) и (16), такова:

X g ( x i , ..., x n ) = { x g G X g ( x " , ..., x n ) : x " G X i ( x g ) , ..., x n G X n ( x g ) } , X e ( x " ) = { x e G X e ( x o ) : x " G X g ( x " , ..., x O_ " ,x e ,x O _+i , ..., x n ) } .

При фиксированных равновесных компонентах составного вектора управлений (13) все условия, записанные в (17) после двоеточий, представляют собой дополнительные ограничения на отклоняющиеся аргументы составного вектора, порожденные условием (14) совокупной допустимости управлений. Например, условие x " G X i ( x g ) из верхней строки (17) надо понимать как неявное ограничение на отклоняющийся аргумент x g в (15). Все такие дополнительные ограничения желательно представить в явной форме, разрешив их относительно отклоняющихся аргументов. Дополнительные ограничения могут оказаться активными или неактивными, поэтому в общем случае X g С X g и X e С X e , где строгое включение реализуется при наличии хотя бы одного активного дополнительного ограничения. Тем не менее для краткости всегда будем называть X g и X _e суженными множествами индивидуальной допустимости.

Если бы выделенному участнику инновационного проекта были известны равновесные выборы всех остальных участников, то свой равновесный выбор он бы нашел, решив только свою традиционную задачу оптимизации (15) или (16) с расшифровкой (17) множества допустимости для своего аргумента, названного выше отклоняющимся. Однако равновесные выборы окружения выделенный участник пока не знает, а от них зависит и его функция полезности, и суженное множество индивидуальной допустимости, на котором он ищет максимум.

В такой ситуации каждому e -му участнику придется сделать заготовку своих наилучших ответов x e на всевозможные допустимые варианты выборов его окружения x __e , то есть построить собственную максимизирующую стратегию x e = ^ ( x __e ), многократно решив свою задачу оптимизации (15) или (16), всякий раз по-разному назначая «чужие» функции x __e :

максимизирующая стратегия соинвесторов ( e = 0):

x g = ^ g ( x i , ..., x n ) G Argmax F g ( x g ; x e )     при      x e = ( x i , ..., x n ) = fix G X e ; (18)

xoGXo максимизирующие стратегии кредиторов (e G E = {1, ..., n}):

x e = ^ e ( x o ) G Argmax F e ( x e ; x q )     при      x q =     fix      G X q .           (19)

x e ∈ X e

Такую работу каждый участник проекта может проделать самостоятельно. Но после этого все результаты (18, 19) нужно свести в одну согласующую систему уравнений:

x q = ^ o ( x i , ..., x n ) G X o ( x i , ..., x n ), x i = y i ( x o ) G X i ( x o ) , ...

xn — ^n(x0) G Xn^O), которую лучше решать коллективно или поручить ее решение доверенному эксперту.

Если система (20) относительно неизвестных функций или параметров x q , x i , ..., x n имеет решение, то оно и будет равновесным x ^o . Геометрически оно означает точку пересечения всех максимизирующих стратегий (18, 19) в пространстве составного вектора (13), поэтому от нее ни одному участнику не выгодно отклоняться, что и требуется в определении равновесия (15, 16). В случае единственности коллективно найденного равновесного вектора x ^o остается раздать соответствующие его компоненты каждому участнику игры для реализации.

Замечания. В принципе каждый участник, стремясь к самостоятельности, может индивидуально проделать одну и ту же работу, решив относящиеся ко всем задачи (15, 16) и (20). Правда, для этого нужно, чтобы все участники снабдили друг друга точными и исчерпывающими сведениями о своих функциях полезности и о множествах своих допустимых управлений. Но лишь в случае единственности решения системы (20) не потребуется дополнительных коллективных действий, если не считать таковыми уже принятое соглашение о соблюдении всеми участниками условия совокупной допустимости управлений.

В случае же неединственности равновесного составного вектора управлений x ^o надобности в коллективных решениях не избежать по следующей причине. Разные варианты равновесного вектора x ^o сулят одному и тому же участнику разную полезность, и он, естественно, захочет предпочесть вариант с большей своей полезностью. Для других участников более предпочтительными могут оказаться другие варианты вектора x ^o из (20). А если составить вектор (13) из компонент, принадлежащих разным вариантам равновесного вектора x ^o , то получившийся вектор, как правило, уже не будет равновесным. Счастливое исключение представляют собой антагонистические игры, когда в них оказывается несколько седловых точек, то есть равновесий, — там и полезности не меняются, и перемешивание компонент не нарушает равновесия.

Коллективные меры также нужны против участников, отклоняющихся от равновесия. Поодиночке им отклоняться невыгодно, что сразу заложено в определение равновесия. Но несколько участников могут вступить в сговор друг с другом с целью получения выгоды за счет согласованности своих, сразу нескольких, отклонений от общего равновесия. А такая возможность не исключается.

Наконец, самым существенным препятствием для реализуемости привлекательной идеи нэ-шевского индивидуализма представляет собой возможность отсутствия решений у согласующей системы уравнений (20). Известные достаточные условия существования равновесий [10] стесняют благоприятную ситуацию рамками непрерывности и выпуклости, быть может, и не очень зауженными. Во всяком случае, рассматриваемая игровая задача о финансировании инновационных проектов с некоторыми дополнительными оговорками сюда помещается.

Но если равновесие в игре все же отсутствует, то требуются коллективные переговоры о смене самого принципа принятия решений.

• V.    Кооперативное решение

Представленный в п. 4 анализ нэшевского игрового равновесия, исходно задуманного как способ индивидуального принятия решений, свидетельствует о необходимости использования участниками игры ряда коллективных действий без которых невозможно реализовать равновесие.

Именно элементы коллективизма позволяют также поднять равновесные выигрыши участников, как правило, выше (в общем случае не ниже) уровня гарантированных результатов, достижимых строго индивидуально. Более широкое использование коллективных действий открывает перспективы дальнейшего увеличения выигрышей участников.

Возможное увеличение выигрышей в кооперативных решениях объясняется объединением всех ресурсов управления, исключением ряда индивидуальных ограничений и нацеливанием объединенных ресурсов на некий общий результат, допускающий последующий справедливый дележ между участниками. Конечно, это достигается ценой усложнения системы управления и наносит некоторый моральный ущерб участникам, вынужденным еще в большей мере отказываться от независимости в принятии решений, чем при реализации идеи игрового равновесия.

Решив объединиться по делам финансирования инновационного проекта, участники, естественно, будут стремиться максимизировать сумму всех чистых доходов в надежде после справедливого дележа увеличить свой индивидуальный доход. При этом они, наверняка, смогут договориться о единой норме дисконтирования А будущей ценности денег: A e = A V e = 0 , 1 , ..., n .

В результате суммирования по номеру участника e их чистых дисконтированных доходов F _e из (9, 10) встречные финансовые потоки u _e и v _e , внутренние для сообщества и названные в п. 2 вторичными, взаимно уничтожаются, поэтому в суммарном чистом дисконтированном доходе F инвестиционного сообщества останутся только внешние потоки u и v , связывающие сообщество непосредственно с проектом и названные первичными:

T

F =

n

X F e = [^[v(t) - ^u(t)] e =0

e -λt dt

~ max ,

где A = fix      >  0 .

В дополнение к соглашению о единой норме дисконтирования λ участники инвестиционного сообщества договариваются об одинаковом уровне I приемлемой доходности: I e = I Ve = 0 , 1 , ..., n . Чтобы каждый участник при последующем дележе смог достичь договорного уровня доходности I , необходимо обеспечить такую же доходность инвестиционного сообщества в совокупности. Это необходимое условие получается почленным суммированием неравенств (7, 8) при I e = I , в результате чего, как и в (21), исчезают все внутренние финансовые перетоки:

TT

0         t > I 0

где I = fix >  1 , A = fix      >  0 .     (22)

Индивидуальные инвестиционные счета S _e всех членов сообщества объединяются в единый инвестиционный счет S всего сообщества, поэтому все балансы и ограничения (5, 6) суммируются по e , что опять исключает внутренние перетоки:

S(t) = X Se(t) = So(O) + e=0

t

|[v ( t ) — u ( t )] dT >  — m ( t ) Vt E [0 ,T ] , 0

где S o (0) = fix >  0 — начальное состояние счета у соинвесторов (у кредиторов полагалось S _e (0) = 0 ,e = 1 , ..., n ), m ( t ) = m i ( t ) + ... + m _n (t) = fix > 0 — суммарная нижняя граница временно невозвращенных долгов, допускаемых кредиторами (для соинвесторов всегда должно быть S o ( t ) >  0).

В объединяющей задаче отыскивается максимум суммарного чистого дисконтированного дохода (21) по первичным расходам u и доходам v при соблюдении условий (1), (2) инженернотехнической допустимости проекта и условий (22), (23) его финансовой допустимости с позиции инвестиционного сообщества в целом:

F ( u,v ) ^ max — целевая функция ( u,v ) E С = { ( u,v ) :     удовлетворяют

(19) ,

(1) , (2) , (22) , (23) }

— множество допустимых управлений.

Это — классическая задача оптимизации. У нее значительно меньше «подводных камней», препятствующих существованию решения, чем у задачи (17) об игровом равновесии.

Решив задачу (24), можно приступить к дележу найденного максимального суммарного дохода F ^∗ между участниками инвестиционного сообщества.

Формализацию интуитивно понятного термина «справедливый дележ» производят по-разому. Один из простейших вариантов — поделить суммарный доход F ^∗ пропорционально индивидуальным равновесным выигрышам W _e ^o из (15, 16), если они существуют. Тогда e -й участник получит

W ^o                            .

F e = Й70Т Zwo ^F ,^e = ^0, ...,n, F = max max F⁽u,v ) .              (25)

W q + ... + w _n                                 ( u,v ) eC

Результат (25) для каждого участника инвестиционного сообщества не хуже равновесного (обычно лучше), поскольку в объединяющей задаче (24) меньше ограничений и связей, чем в (15, 16), (20), и в ней максимизируется сразу суммарный доход, а не его составляющие по-отдельности при фиксированных чужих управлениях, как в (15, 16).

Если решение задачи (15, 16), (20) об игровом равновесии существует или получение такого решения затруднительно, то для подсчета долей участников в дележе (25) можно использовать их максимальные гарантированные результаты W _e , действительно индивидуальные и притом всегда существующие (но как правило невысокие):

W e = max[inf F ( x e ; x -e )] ,                                    (26)

xe x-e где неуказанные множества изменения своих xe и чужих x-e управлений строятся с учетом условий индивидуальной и совокупной допустимости по схеме из [8], несколько отличной от примененной в п. 4 для задачи игрового равновесия.

После того как произведен дележ (25), нужно еще вычислить вторичные финансовые потоки, его обеспечивающие с учетом всех исходных условий (5, 6), (7, 8), а не только их просуммированных вариантов (16), (17), учтенных в объединяющей задаче (24). К сожалению, это не всегда удается сделать.

• VI.    Заключение

• 1.    Вопросы инженерного проектирования и финансовой реализуемости инноваций следует решать совместно. В результате независимого инженерного проектирования даже социально и экономически значимый проект может оказаться в рыночных условиях нереализуемым. Однако финансово сбалансированный сдвиг инженерного оптимума в сторону уменьшения расходов на проектирование и производство новой технической системы, сопровождающийся, конечно, некоторым уменьшением доходов от эксплуатации менее совершенной системы, может обеспечить проекту финансовую реализуемость, что будет количественно показано авторами в очередной статье.

• 2.    Качественный анализ широко распространенных показателей эффективности инвестиций, таких как чистый дисконтированный доход и индекс относительной доходности, говорит о целесообразности их одновременного использования, поскольку первый из них характеризует абсолютную успешность вложений, а второй — относительную.

• 3.    Взаимодействие соинвесторов и кредиторов, участвующих в финансировании инновационного проекта, уместно формализованно описывать как игровое, уделяя особое внимание специфическим ограничениям на управления, связывающим участников друг с другом.

• 4.    Связывающие ограничения неминуемо привносят в игру элемент коллективизма из-за необходимости обеспечить совокупную допустимость управлений участников, даже когда в качестве схемы их рационального поведения принимается исходно индивидуалистическое равновесие по Нэшу. Впрочем, и без связывающих ограничений нэшевское равновесие требует коллективных действий в случае неединственности положения равновесия и для противодействия участникам, которые могут попытаться отклониться от согласованного положения равновесия.

• 5.    Невозможность обойтись без коллективных действий при поиске и реализации нэшевского равновесия делает более привлекательными кооперативные решения, в которых максимизируется суммарная прибыль участников, а затем осуществляется ее дележ, обещающий каждому участнику результат, не худший (а, как правило, лучший) индивидуально достижимого. Но при этом нужно еще сформировать допустимые вторичные финансовые потоки между участниками, что не всегда оказывается возможным.

• 6.    Представленные в статье игровые постановки проблемы совместного разрешения инженерных и финансовых аспектов инновационного проектирования требуют дальнейшего анализа. Сначала аналитического — на иллюстративных примерах, а затем численного — на прикладной задаче, над чем и работают авторы.

Авторы благодарны рецензенту за полезные замечания.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 09-07-00343-а).