Finding Longest Common Substrings in Documents

Published Online August 2015 in MECS

There are many methods and algorithms to compare documents or simply to judge similarity between documents. Such algorithms are time and space consuming, for instant the brute force algorithm compares two documents in word by word manner. The classic textbook solution to the longest common substring (LCS) problem is to build the (generalized) suffix tree of the documents and find the node that corresponds to LCS [18]. While this can be achieved in linear time, it comes at the cost of using huge space to store the suffix tree. In applications with large amounts of data or strict space constraints, this renders the classic solution impractical.

Another algorithms compare the subject document with investigated documents by constructing metrics related to the documents such as punctuation, the number of statements, paragraphs [9].

LCS approaches aid the problem of searching for coding regions in DNA sequences yielding the common substring between DNA sequences [10, 15].

The problem of LCS can be defined mathematically as:

Given two documents (strings), S of length m and T of length n , find the longest strings which are substrings of both S and T .

A generalization is the k-common substring problem [16].

Given the set of strings = {S1S2,, ... ,Sk }, where |S, | = n , and £ n , = N. Find for each 2 < к < К, the longest strings which occur as substrings of at least strings.

The algorithm suggested in this paper aims to minimize both the time of processing and the size of allocated memory. The algorithm detects not only the longest common string but finds exactly all possible common substrings. It is based on the convolution between the two documents (named major sequence ( X ) which is represented as array and the minor one ( Y ) which is represented as circular linked list. An array ( Z ) of linked lists is established and a new node is created for each match between two substrings. The first string is kept fixed while the another one is rotated, using pointer, to left in one character step. If two or more matches in different locations in string Y share the same location in string X , the corresponding nodes will construct a unique linked-list. Accordingly, by the end of processing, we obtain a group of linked-lists containing nodes arranged in certain manner representing all possible matches between sequences X and Y . The array Z of linked lists is then traversed horizontally and vertically looking for the matches between string X and Y .

The rest of the paper is organized as follows. Section II discusses the suggested algorithm, and the implementation and experimental results are discussed in Section III. We conclude the paper in Section IV.

• II.    The Suggested Algorithm

The suggested algorithm compares two documents to find all possible identical matches. The data structure required for the suggested algorithm is shown in Fig.1. The major string is represented in array X while the second one (the minor string) is represented in circular linked-list Y . Each node in the circular linked list Y consists of two fields: the first field holds character value while the second one points to the next node in a circular manner. The initialization process (shown in Fig.2) reads the major document (the longer one) character by character in array X (each array cell holds one character value) and the minor document is read into the circular linked-list Y respectively. In addition, it establishes an empty linked-list array Z , where each cell of array Z is a separate linked-list. The data structures X , Y and Z are all of the same size as the major document (measured in characters). The major document refers to the longer one. If the major document is longer than the minor one, the rest of the circular linked-list Y will be filled with a not used special character (i.e. Null ).

The process of matching is described in the flowchart shown in Fig.3; where it begins by creating two counters: I for loop number and shift_no for the shifting number. Two nested loops will be used, one for left-shifting the sequence represented in the circular linked-list Y, and the inner loop for comparing every character in X with the corresponding one in Y . If there is a match between the the character stored in cell number n in X and the character stored in node number n in the shifted circular linked-list Y , then a new node will be added to the linked-list stored in cell number n in array Z . The new node consists of two fields; the first one contains the shift number ( shift_no counter) and the second one contains a pointer to the next node in the same linked-list (it must be null until adding new node).

The last process scans and inspects the contents of the linked-list array Z looking for the contiguous nodes which contains the same shift_no in its data fields. The result of this process is added to a list yielding the longest contiguous nodes sequence.

The following example illustrate the matching process of the suggested algorithm:

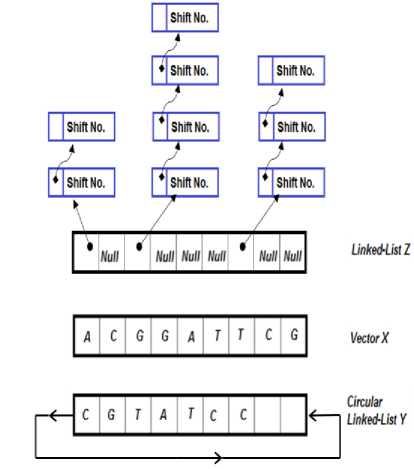
Fig.1. The data structures used in the suggested approach

Input: two strings

Major string = “ please let me learn better”

Minor string = “ release letter”

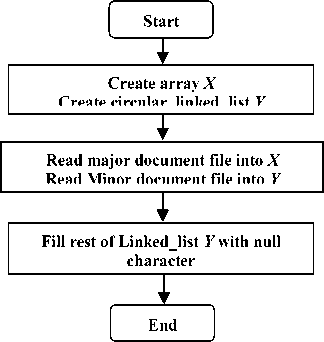
Fig.2. Flow chart of the initialization process

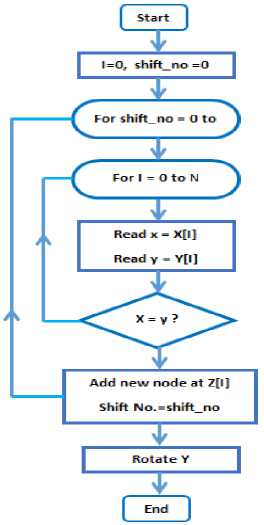
Fig.3. Flow chart of the matching process

As illustrated in Fig.5 B, the first two rows at top of the right table contain the two input strings X and Y respectively. The minor string is rotated to left one character at a time yielding to the successive strings shown in the rest of the same table. The convolution process is performed every time the minor string is rotated, the contents of the minor string is compared, character by character with the corresponding characters of the major string yielding to the corresponding row in the left table

(Fig.5 A) in the figure. If two characters are equal, a new node is added to the linked list related to this position in the major string. The new node contains two fields: the first one contains the shift_no and the other contains a pointer to the next node (null until adding the next node). The new node is represented by “ 1 ” in the left table. The two linked-lists shown in Fig.4 represent the added nodes in the second and third columns of the left table (Fig. 5 A) respectively and they are corresponding to characters “ l ” and “ e ” of the major string. Inspecting the rows contained in the left table, it is noticed that each row represents the result of comparing the major string with the minor one at certain rotation number. The “ ones ” in a row means that the corresponding characters in both strings are equal. The contiguous “ ones ” means that the corresponding characters is common substring in both strings. For example the ones in the row number “ 1 ” in the left table represents the substrings: “ lease let ”, “ ” and “ r ” respectively.

Fig.4. the added nodes in the second and third columns of the left table corresponding to characters “l” and “e” of the major string

Shift No.	Result of comparing major string with the rotated minor string
0													1							1
1		1	1	1	1	1		1	1	1										1						1
2										1										1
3														1										1	1
4			1			1			1		1			1						1
5											1			1						1					1
6											1			1						1		1
7		1	1			1					1			1
8							1				1			1						1		1			1
9							1				1			1				1		1
10			1				1				1			1
11							1				1			1						1		1			1
12							1				1			1		1
13							1				1													1
14											1				1	1	1					1	1	1	1	1
15							1				1		1	1									1
16							1
17							1						1			1						1
18							1
19							1		1
20													1		1	1		1
21								1	1
22						1												1		1
23											1		1			1				1
24						1			1											1
25			1																	1

A)

Fig.5. Illustration example to find matches between strings: ”please let me learn better” as major string and “release letter” as minor one

• III.    Implementation and Experimental Results

The suggested algorithm has been implemented using C# (Microsoft Visual Studio) language to perform comparison between two input long strings and display all possible common substrings in suitable manner. The program has been tested with different lengths strings and the time of processing is computed in each case. The snapshot in Fig.6 is taken after running the program for the example explained in Fig.5. The resulted common substrings between the two input strings are listed in the data view component as shown in the mentioned Fig. along with the locations of those substrings and their lengths in both input strings. The relation between the time of processing and its dependence on the ratio between the lengths of both minor and some major strings

(see Table-1) have been experimentally studied yielding to Table-2 which is presented and plotted in Fig.7. The major string was 1000 character and the minor string is varied gradually from 50 to 1000 characters length. It is noticed that this relation is almost linear. Moreover, the time of processing has been studied in more deep: the time of processing consists of two components; the first one is consumed in constructing the linked lists related to each position in the major string which contains the matches between the two strings, and the other component is consumed in traversing the these linked lists looking for continuous strings. It has been found that the first time component is trivial compared to the second one (Table-2). The relation between time of processing and its dependence on the length of the major string is considered and inspected yielding to Table-3 which is represented in Fig.8 respectively.

Table 1. LCS for different input strings

Major string	Minor string	LCS
please let me learn better	release letter	Lease let
A state diagram is a model of a reactive system. state diagrams are used to model complex logic. The model defines a finite set of states and behaviors and how the system transitions from one state to another when certain conditions are true.	state diagrams are used to model complex logic in dynamic systems from one state to another	state diagrams are used to model complex logic
we can format hard disk	information science	format
his computer is encoded	the letter is enclosed	ter is enc
this manual machine is very old	the computational machines	Al machine

Table 2. Relation between time of creating linked lists and traversing them (length of major string = 1000 characters).

Minor string length	Time of creating linked list	Time of traversing linked list	Total time (seconds)
50	16	1597	1613
100	24	1879	1903
150	29	2311	2340
200	30	2847	2877
250	34	3211	3245
300	35	3688	3723
350	36	4380	4416
400	36	5094	5130
450	37	5988	6025
500	37	6957	6994
550	37	8649	8686
600	37	10400	10437
650	37	11505	11542
700	37	13042	13079
750	37	15264	15301
800	37	16389	16426
850	38	17689	17727
900	38	18770	18808
950	38	20349	20387
1000	40	21422	21462

Table 3. Relation between total processing time and length of string (both minor and major strings are of the same size).

Minor string length	Time of creating linked list	Time of traversing linked list	Total time (seconds)
200	4	277	281
400	8	966	974
500	16	1710	1726
600	22	2705	2727
700	26	4197	4223
800	29	7596	7625
1000	37	19188	19225
1200	75	34815	34890
1500	119	64296	64415
2000	300	155075	155375
2250	442	224355	224797
2500	576	310108	310684
3000	976	530132	531108
4000	1779	1340481	1342260
4500	2111	1919311	1921422
5000	2695	2656767	2659462

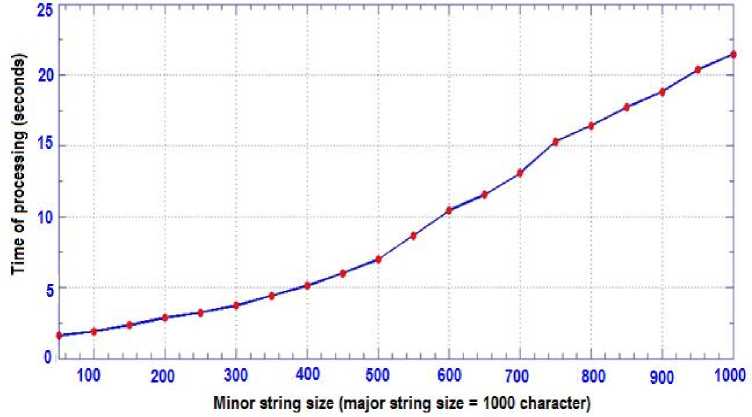
Fig.6. The snapshot of the implemented program running for the illustration example.

Fig.7. The relation between the time of processing and its dependence on the ratio between the lengths of both minor and some major strings

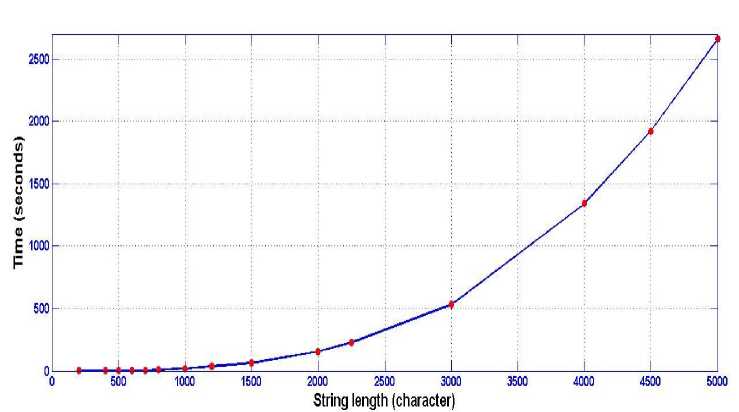
Fig.8. Relation between time consumed in constructing linked lists and time consumed in traversing them

• IV.    Conclusion

Documents matching is a fundamental and upcoming area in data processing and internet search. The algorithm proposed in this paper addressed the problem of locating the longest common substring (LCS) in two different sequences. It is based on the convolution between the two strings (named major sequence X and minor one Y ) and creating a node to the linked-list in the corresponding cell of array Z for each match between two substrings. If two or more matches share the same location in string X , the corresponding nodes will construct a single linked-list yielding to a group of linked-lists containing nodes arranged in certain manner representing all possible matches between sequences X and Y . The obtained results presented very good speedups and indicate that impressive improvements has been achieved. basing on this algorithm, an application can be developed to find the longest common substring between two or more DNA sequences. The prposed algorithm can be developed to locate the longest common strings between the major document and several minor strings. Moreover, the algorithm needs to be developed to be able to run in parallel processing manner to cope with the long time processing problem.