Finding Optimal Routes in Internal Routing Networks based on a Modified Dijkstra’s Algorithm

Modern networks are facing an unprecedented increase in traffic volumes, driven by the proliferation of new services and the growing number of connected devices. Analysis of traffic from large operators shows a steady increase in load, especially due to the popularity of video applications and other bandwidth-intensive services [1, 2]. This increase in load creates significant challenges for the effective management of network resources and can lead to congestion in certain parts of the network, negatively affecting the quality of service (QoS) [3].

The Standard Interior Gateway Routing (IGP) protocols, for instance Open Shortest Path First (OSPF) [4], generally employ the Dijkstra's algorithm to calculate a single Shortest Path First (SPF) tree, thereby determining the optimal routes from a source to all other nodes in the network. However, focusing on only one shortest path to each node often leads to excessive traffic concentration on certain network segments. This, in turn, reduces the efficiency of using alternative routes, creates bottlenecks in the network, limits the overall throughput, and reduces its fault tolerance.

One of the most promising approaches to solving these problems is multipath routing. This concept involves the use of several available paths to transfer data between two network nodes. The use of such routing allows for more efficient distribution of network traffic between different routes, which contributes to better load balancing and avoidance of congestion on individual channels [6]. Furthermore, the availability of alternative paths significantly increases network reliability, since in the event of a failure of one of the channels or nodes, traffic can be quickly redirected through other available routes. This ensures fast communication recovery and minimizes packet loss. Dividing the data flow between multiple paths can also potentially speed up data transfer by making more efficient use of the total network bandwidth.

Despite the existing approaches to multi-path routing, most of them do not allow storing alternative routes to all network nodes or require significantly higher computational costs. This paper solves the problem of constructing a set of shortest routes with low computational complexity and the ability to store the results for further use. The proposed modification of Dijkstra's algorithm allows us to build not only the main SPF tree, but also a second additional shortest path tree covering all network nodes. This allows the router to have at least two independent paths to each node, which contributes to better load balancing and increased reliability. At the same time, the algorithm retains the same computational complexity as the classical Dijkstra algorithm, requiring only twice as much memory to store the results. Thus, the hypothesis of this paper is that the construction of a second SPF tree allows for the implementation of efficient multi-path routing without significantly complicating the computational process.

2.    Literature Review

Lan et al. (2012) [7] consider the problems of single-path routing in OSPF, such as slow response to congestion and inefficient use of network resources. They propose a multi-path routing algorithm (DSMC) based on several link metrics such as bandwidth and propagation delay. The simulation results show the advantages of the proposed algorithm in terms of better load balancing, lower queuing delay, and better average network utilization compared to standard OSPF.

Moza and Kumar (2020) [8] note that to ensure high quality of service (QoS) in networks, especially for multimedia applications, it is necessary to find paths that satisfy certain constraints (reliability, throughput, delay). This paper proposes to use a genetic algorithm to determine the K shortest paths from one source to one or more destinations, taking into account the bandwidth constraint. The algorithm uses the connection matrix and channel bandwidth to find paths, which allows to increase the throughput and packet delivery ratio.

RFC 8218 (2017) [9] describes an extension to the Optimized Link State Routing Protocol Version 2 (OLSRv2) that adds support for multipath routing. The appendix provides an example of the Multipath Dijkstra’s algorithm, which, after finding the first shortest path, increases the channel metrics of this path and runs the Dijkstra’s algorithm again to find the next, potentially not completely disconnected path. This approach is aimed at avoiding the selection of significantly worse, though fully disconnected, paths for a better balance between paths.

Waoo et al. (2014) [10] present an improvement of the standard AODV routing protocol for mobile ad-hoc networks. Their mechanism establishes and stores multiple optimal paths based on throughput and delay criteria. In the event of a communication channel failure, the system switches to the next available path. To establish multiple paths, information from RREQ packets is used, and RREP packets are sent over more than one path. This reduces the overhead of local route discovery in the event of a link failure, resulting in lower latency and packet loss ratio compared to AODV and HLSMPRA.

Chen et al. (2020) [11] propose an efficient algorithm for finding K shortest simple paths (without loops) in road networks. The algorithm formulates the process of calculating deviation paths as a repeated search for the shortest path in a dynamic network. The reoptimization technique (Lifelong planning A*) is used, which allows to efficiently calculate each deviation path by reusing the shortest path tree created during the previous search. Experiments on real road networks have shown significantly better performance compared to other state-of-the-art algorithms.

Li et al. (2008) [12] propose a new routing algorithm for wireless sensor networks (WSNs) called Data Centric Braided Multipath (DCBM). The algorithm aims at achieving and maintaining route stability through multiple interconnected paths that can cope with node mobility. It uses several channel metrics to select paths, balancing data delivery quality with energy efficiency. Simulations show that the algorithm maintains a delivery ratio similar to previously proposed protocols, but requires significantly less control packet overhead and has loop reduction and local path recovery properties.

Liu and Liu (2010) [13] propose a delay-aware multi-path routing protocol (DMSR) to support QoS for real-time multimedia applications in wireless ad-hoc networks. The metric for path selection is based on local node delay information, which takes into account the number of neighboring nodes, channel occupancy time, and the number of packets in the sending buffer. The simulation results show that the DMSR protocol can reduce the average end-to-end delay compared to the DSR and i-DSR protocols.

Farrugia et al. (2018) [14] use a multi-objective genetic algorithm to solve the Multi Commodity Flow routing problem in software-defined networks (SDNs). Unlike linear programming (LP), which can lead to packet reordering that negatively affects TCP, the genetic algorithm allows finding solutions with fewer flow splits while maintaining the trade-off between overall network flow and path cost. This improves flow-level performance by reducing the packet reordering problem and solves LP scalability issues.

Kudtarkar et al. (2014) [15] describe a singular multihop routing based on a spindle graph and the Labelle Merging Algorithm. This approach is aimed at overcoming the disadvantages of single-path OSPF routing, such as congestion and inefficient use of resources. Singular multihop routing offers a compromise, increasing fault tolerance and load balancing. The algorithm finds and merges duplicate paths with small differences to make efficient use of resources.

3.    Characterization of the Dijkstra’s Algorithm and its Implementations

Dijkstra's algorithm [16] is a classical method for finding the shortest paths from one source to all other vertices in a graph with non-negative edge weights. It belongs to greedy algorithms and guarantees finding optimal routes if the priority queue is handled correctly. It is widely used in routing systems, in particular in the OSPF protocol, where it performs the SPF (Shortest Path First) function of building a tree of shortest paths from the router to all network nodes.

There are several implementations of the Dijkstra’s algorithm that differ in their computational complexity depending on the structure of the input data and the data structures used:

• •    Based on a regular array (naive implementation): at each step, a linear search for the minimum distance is performed, so the total complexity is

O(V2)(1)

where V is the number of vertices in the graph.

• •    Based on the Binary Heap: improves the efficiency of finding the minimum element, which reduces the overall complexity to

O ((V + E )log V)(2)

where E is the number of edges. This is much more efficient for sparse graphs.

• •    Based on Fibonacci heap: has amortized complexity

4.    The Proposed Modification of the Dijkstra’s Algorithm

O (V log V + E)(3)

Theoretically the most efficient implementation, but rarely used in practice due to the complexity of implementation and large hidden constants.

The best compromise between performance and implementation complexity is to use a binary heap (or priority queue), which provides good performance in real networks and is supported in most standard programming language libraries.

The proposed approach enhances the classical Dijkstra’s algorithm by enabling the identification of multiple routing paths between network nodes within a single execution. The core idea lies in preserving not only the primary shortest routes but also viable alternative routes that can be employed in the event of congestion or failure of the main paths. Importantly, this enhancement is achieved without altering the fundamental computational complexity of the original algorithm.

In contrast to the traditional implementation, which constructs a single shortest path tree, the modified algorithm generates a set of trees: one main tree and one or more alternative trees. These alternative trees store backup routes that may not be optimal under normal conditions but can serve as valuable alternatives when needed:

• •    First condition. If a new, shorter route to a node is found during the algorithm, the previous route is not discarded but stored in an additional tree as a backup. Thus, the main tree always contains the most optimal routes, and additional trees contain alternatives.

• •    Second condition. If the new route found is longer than the main route but shorter than one of the existing routes in the additional trees, it is also saved. The algorithm sequentially checks each of the additional trees, and if any of them has a higher path weight, the new route replaces the old one.

To illustrate the effectiveness of this proposed method, an example is presented using a graph with 13 nodes (Fig. 1). The execution of the algorithm on this graph results in the formation of the primary shortest paths tree (Fig. 2), which, as expected, mirrors the output of the conventional Dijkstra’s algorithm in terms of the shortest paths. However, the crucial distinction lies in the simultaneous generation of an additional tree of routes (Fig. 3). This additional tree explicitly contains the alternative pathways to the nodes that were identified and stored according to the two conditions during the algorithm's single execution. This demonstrates the method's ability to provide valuable routing alternatives alongside the primary shortest paths.

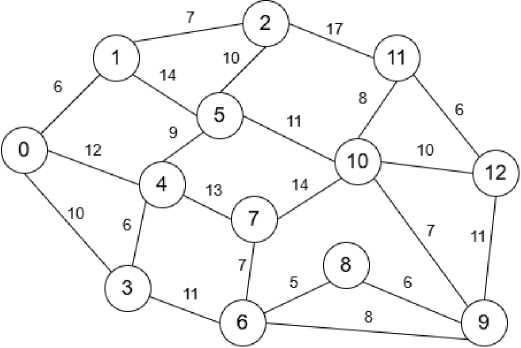
• Fig.1.    Nodes network

  

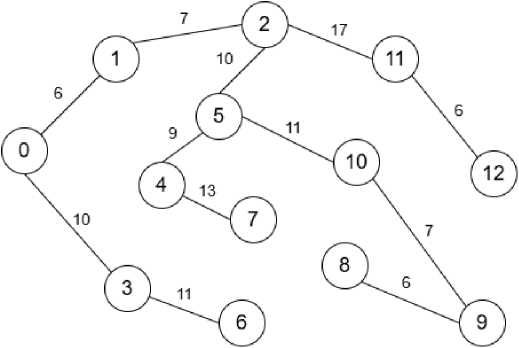
• Fig.2.    Main shortest-path tree

  

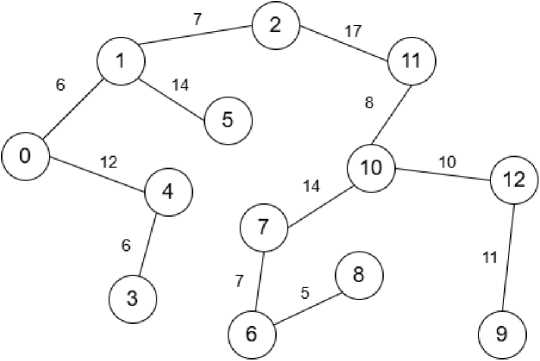
• Fig.3.    Additional shortest-path tree

5.    Experiment and Results Analysis

• 5.1.    Analysis of the Algorithm Efficiency

Fig. 4 presents the general scheme of the proposed modification, which builds upon the classical Dijkstra’s algorithm implemented with a priority queue.

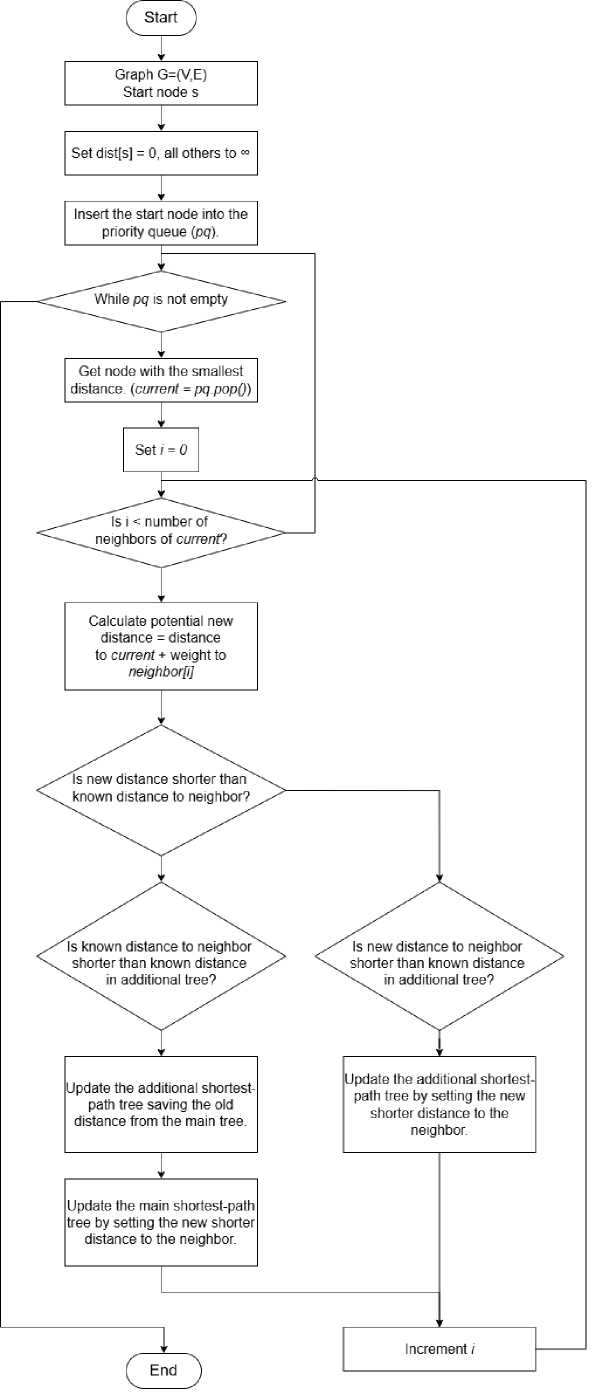
Fig.4. Flowchart of modified dijkstra’s algorithm

This section presents a comprehensive analysis of the experimental studies conducted to evaluate the effectiveness of the proposed modification of the Dijkstra algorithm. The purpose of these experiments was to compare the performance of the modified algorithm with the classical implementation in terms of two key indicators: algorithm execution time and message delivery time for single- and multi-path transmission. The research included a detailed analysis of the algorithms' performance, including a comparison by execution time, amount of RAM used, and average CPU utilization on test graphs with different numbers of nodes - from 10 to 1000. In addition, the developed modification was compared with other well-known approaches to finding multiple routes, such as Suurballe, Yen, and ant algorithms. These experiments were designed to identify and compare the characteristics of each of the studied approaches in a simulated network environment.

In the first experiment, we comprehensively evaluated the effectiveness of route search algorithms by comparing the classical and modified Dijkstra algorithms in terms of three key performance indicators: execution time (in ticks), amount of RAM used (in bytes), and average CPU load (in percent).

The measurements were made on test graphs with the number of nodes ranging from 10 to 1000, which allowed us to evaluate the behavior of the algorithms in problems of varying complexity. The execution time was recorded as the actual amount of time required to complete the calculations, while the memory consumption was determined by estimating the amount of memory allocated to the process during execution. The average CPU load was calculated as the ratio of the total CPU time spent by the process to the actual execution time of the algorithm, taking into account the number of logical cores. In cases where the algorithm was executed too fast and the measurements gave a load close to zero, the calculations were based on repeatedly running the algorithm in a loop with subsequent averaging of the results, which allowed us to avoid errors and ensure the stability of the metrics.

The experiments were conducted on a hardware platform with the following characteristics:

• •    Processor: Intel(R) Core(TM) i7-9750H CPU @ 2.60GHz

• •    Clock frequency: 2592 MHz

• •    Number of physical cores: 6

• •    Number of logical threads: 12

The measurement results are presented in Table 1. To illustrate the relative increase in the performance of the modified algorithm compared to the classical one, the data are visualized in Fig. 5.

Table 1 Comparison of algorithms

Number of nodes in the network	Algorithm running time (ticks)		RAM used (bytes)		Average CPU load
	The classic Dijkstra’s algorithm	Modified Dijkstra’s algorithm	The classic Dijkstra’s algorithm	Modified Dijkstra’s algorithm	The classic Dijkstra’s algorithm	Modified Dijkstra’s algorithm
10	97	146	680	936	0,0122%	0,0196%
50	930	984	2440	3336	0,0336%	0,0350%
100	3505	3518	5000	6696	0,1759%	0,1773%
200	12244	12408	10480	13776	0,2545%	0,2581%
500	68581	69412	22640	30736	0,7649%	0,7864%
1000	268637	276494	46880	62976	1,8928%	1,9008%

Based on the results presented in Table 1, there is a natural increase in the execution time for both algorithms -both the classical and the modified Dijkstra algorithm - with an increase in the number of nodes in the network. This trend is fully consistent with their theoretical complexity. When analyzed in detail, as shown in Figure 5, the modified algorithm demonstrates slightly faster execution time. For example, for a network with 10 nodes, the increase in execution time is 50.52% compared to the classical algorithm. However, when the network size increases to 100 and 1000 nodes, this difference decreases significantly to 0.37% and 2.92%, respectively.

A similar pattern is observed in terms of RAM consumption, which increases in proportion to the number of nodes. According to Fig. 5, the modified algorithm consistently requires 31-38% more memory over the entire measurement range. This is due to the need to store auxiliary data structures that support alternative routes.

The average CPU utilization also shows a similar trend. While the absolute difference in utilization is not significant, as shown in Table 1, the relative increase for the modified version is noticeable on small graphs, but stabilizes at less than 1% for networks with 100 nodes or more, as shown in Figure 5.

Thus, the modified algorithm retains the scalability of the classical approach while providing additional functionality in the form of support for multiple paths. This is achieved at the cost of a moderate and predictable increase in computing resources.

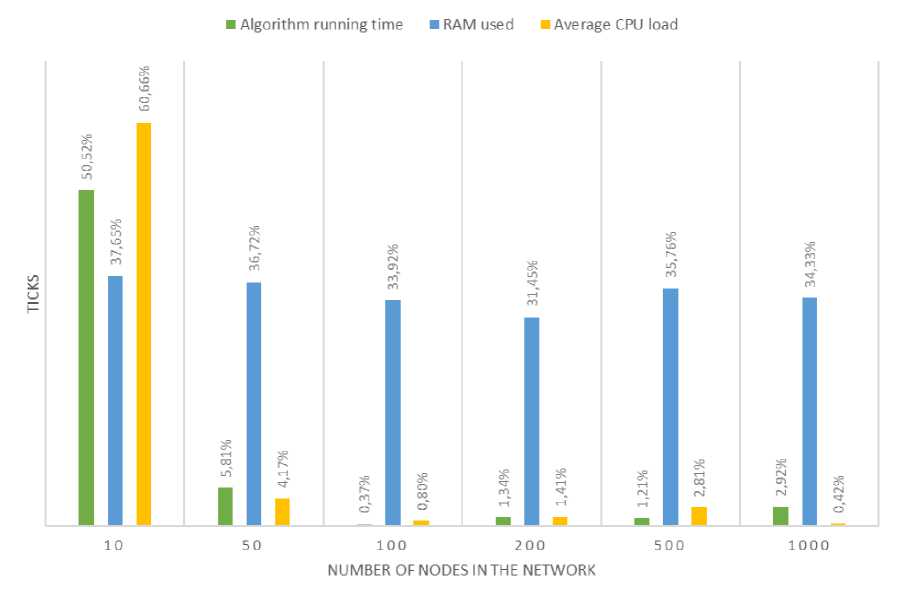
Fig.5. Percentage increase in resource utilization by the modified algorithm compared to the classical one

• 5.2.    Comparison with Alternative Algorithms for Finding Multiple Routes

The second set of experiments focused on comparing the developed modification with other known approaches to finding multiple routes. For this purpose, representatives of different classes of algorithms were chosen: exact, iterative, and heuristic. This approach allowed us to cover a wide range of strategies for solving the problem of routing in graphs. Each of the selected methods was tested on identical input data, which ensured the objectivity of the results and the possibility of direct comparison.

As in the previous section, the main evaluation criteria were execution time, RAM usage, and average CPU load. The results are shown in Table 2 and Table 3.

Table 2. Results of measuring the time and space costs of algorithms

Number of nodes in the network	Algorithm running time (ticks)				RAM used (bytes)
	Modified Dijkstra’s algorithm	Suurballe’s algorithm	Yen’s algorithm	Ant Colony algorithm	Modified Dijkstra’s algorithm	Suurballe’s algorithm	Yen’s algorithm	Ant Colony algorithm
10	146	281	310	9758	936	752	872	304
50	984	2437	1114	99559	3336	2512	2648	336
100	3518	7339	3803	484415	6696	5144	5192	352
200	12408	24936	79987	1357725	13776	10640	10688	368
500	69412	144197	478943	12268371	30736	22800	22848	384
1000	276494	594229	616630	43067105	62976	47040	47120	448

The analysis of the results presented in Tables 2 and 3 reveals clear tradeoffs between the approaches under study. In terms of execution time, the developed modified Dijkstra algorithm demonstrates the highest performance, significantly outperforming its counterparts, especially on large networks. In contrast, the ant algorithm turned out to be orders of magnitude slower, which is a characteristic feature of iterative heuristics that take a long time to converge.

When analyzing the use of RAM, the opposite picture is observed: the ant algorithm is the most economical, while the modified Dijkstra algorithm requires the most resources to store auxiliary structures. Yen and Suurbal's algorithms occupy an intermediate position in terms of both time and space costs. At the same time, the average CPU load remains comparable for all methods and is not a decisive factor in the comparison.

Table 3. Results of measuring the average CPU load

Number of nodes in the network	Average CPU load
	Modified Dijkstra’s algorithm	Suurballe’s algorithm	Yen’s algorithm	Ant Colony algorithm
10	0,0196%	0.0201%	0.0189%	0.0213%
50	0,0350%	0.0362%	0.0345%	0.0380%
100	0,1773%	0.1810%	0.1740%	0.1925%
200	0,2581%	0.2634%	0.2529%	0.2780%
500	0,7864%	0.8033%	0.7698%	0.8125%
1000	1,9008%	1.9284%	1.8841%	2.0017%

It is important to note that a direct comparison of these algorithms is conditional, as they are designed to solve slightly different problems. For example, Yen's algorithm is an exact method that is guaranteed to find K-shortest paths and is indispensable when the optimality of routes is important. Suurbal's algorithm, in turn, specializes in finding two node-intersecting paths, which is critical for ensuring network fault tolerance. The ant algorithm, as a heuristic, does not guarantee optimality, but is well suited for very large and dynamic systems where exact methods are too slow.

Against this background, the developed modification offers a unique approach. Its key advantage is the ability to find the second shortest route not to one endpoint, but to all network nodes simultaneously, allowing this data to be stored as an additional shortest path tree. Thus, the router gets much more options for sending data, having a precalculated backup path for each possible direction. This makes the developed approach especially effective for systems where the speed of response and flexibility of routing are critical.

Table 4. Analysis of message delivery time

Main message (number of packets)	Additional messages (number of packets)	Delivery time of the main message (steps)		Delivery time of all messages (steps)
		The classic Dijkstra’s algorithm	Modified Dijkstra’s algorithm	The classic Dijkstra’s algorithm	Modified Dijkstra’s algorithm
0→12(40)	12→0 (40)	1332	969	1332	1162
0→4(15)	2→8 (35), 11→2 (8), 9→12 (12)	179	76	407	311
2→8 (35)	0→4(15), 11→2 (8), 9→12 (12)	407	311
11→2 (8)	2→8 (35, 0→4(15), 9→12 (12)	135	263
9→12 (12)	2→8 (35), 11→2 (8), 0→4(15)	131	107
3→1(30)	6→2 (15), 12→0 (20), 9→1 (10), 4→9 (20), 1→8 (10)	395	275	552	443
9→1 (10)	6→2 (15), 12→0 (20), 3→1 (30), 4→9 (20), 1→8 (10)	157	250	552	443
1→7(14)	5→8 (20), 8→5 (25), 2→3 (12), 3→2 (18), 6→5 (5), 5→6 (20), 9→5 (10), 5→9 (15)	199	200	790	757
2→3 (12)	5→8 (20), 8→5 (25), 1→7(14), 3→2 (18), 6→5 (5), 5→6 (20), 9→5 (10), 5→9 (15)	297	254
8→5 (25)	5→8 (20), 1→7(14), 2→3 (12), 3→2 (18), 6→5 (5), 5→6 (20), 9→5 (10), 5→9 (15)	790	757

• 5.3.    Analyze the Message Delivery Time

The third experiment, conducted on the graph shown in Fig. 1, aimed to evaluate the impact of using multiple routes found by the modified algorithm on message delivery time compared to using a single path found by the classical algorithm. Several data transmission scenarios with different numbers of simultaneous flows between network nodes were modeled. The delivery time (in simulation steps) was measured both for the selected message and for all messages in the scenario. The results are presented in Table 4.

The analysis of the data presented in Table 2 shows that the use of multi-path routing has a significant positive impact on the total delivery time of all messages, especially when the network is loaded with additional messages. In most cases, the total delivery time of all packets is significantly reduced compared to the classical approach. For example, for a 3→1 message (30 packets) combined with five additional messages, the total delivery time is reduced from 552 to 443 steps. This is made possible by distributing message packets along parallel routes, which avoids creating bottlenecks and makes more efficient use of network bandwidth.

However, as can be seen from the same table, the use of multiple routes can have an unobvious impact on the delivery time of the main message. In some scenarios, the delivery time of the main message when using the modified algorithm may be longer than when using the classical algorithm, despite the fact that the total delivery time of all messages is less. For example, for the 11→2 main message (8 packets) combined with three additional messages, the delivery time of the main message increased from 135 to 263 steps. A similar situation is observed for a 9→1 message (10 packets) with five additional messages (from 157 to 250 steps).

This behavior, where the message delivery time increases when using multipathing, can be explained by several factors:

Firstly, even if the first packet of the main message is sent by one of the routes, the other routes may be busy with packets of other messages that are also being processed at that moment. This can create time delays that are different from the single route scenario, where all traffic for a given pair of nodes travels along a single path.

Secondly, when using multiple routes, the router spends additional time deciding on the optimal route to send each packet, taking into account the current congestion of alternative routes.

Despite the possibility of such an increase in the delivery time of the first packet in some cases, the overall effect of using multipathing for packet transmission is positive. A significant reduction in the total delivery time of all message packets and additional messages indicates the effectiveness of this approach for increasing the overall throughput and speed of large data transfers or processing multiple simultaneous requests in the network.

6.    Summary and Conclusions

In this paper, we propose and study a modification of the classical Dijkstra algorithm aimed at the efficient implementation of multi-path routing in internal routing networks. The key advantage of the proposed approach is the ability to find not only the main shortest path, but also a set of alternative routes to all network nodes in one run of the algorithm without changing its asymptotic complexity. This makes the algorithm promising for integration into modern communication systems, where the flexibility of traffic distribution and stability of operation are critical.

Experimental studies have confirmed that the proposed modification maintains high performance, only slightly increasing the execution time and moderately consuming more RAM compared to the classical implementation. At the same time, the main advantage is manifested during data transmission under high load conditions: the use of alternative paths can significantly reduce the total message delivery time. This contributes to a more efficient use of network bandwidth, reduces the risk of congestion, and improves overall performance. It was also found that in some scenarios, the delivery time of a particular message may increase due to competition for resources on parallel routes, but the overall effect on a system with heavy traffic remains positive.

The proposed algorithm has significant potential for implementation in internal routing protocols, such as OSPF, as an addition to standard SPF mechanisms. Its application can significantly increase network fault tolerance, as precalculated backup paths ensure fast communication recovery in case of failures. In addition, it opens opportunities for more intelligent load balancing, allowing network devices to dynamically distribute data flows based on the current state of the channels. In the long run, such algorithms can become the basis for developing more adaptive and selforganizing network infrastructures.

Further research can be developed in several directions. First, it is worth focusing on optimizing the criteria for selecting alternative paths by integrating additional metrics such as delay, throughput, channel reliability, or transmission cost. Secondly, it is promising to study the adaptation of the algorithm for dynamic environments, such as software-defined networks (SDN), the Internet of Things (IoT), and mobile networks, where the topology can change in real time.