Fire resistance of statically indeterminate steel systems

The problem of fire resistance of steel structures was dealt with by many researchers, such as A.I. Yakovlev, V. P. Bushev, V. A. Pchelintsev, V. G. Olimpiev, N. F. Gavrikov, S. V. Davydov. O.Peterson, S. Magnusson, J. Thor. and others.

• V . P. Bushev, V. A. Pchelintsev in his research had developed methods of testing building constructions of buildings for fire resistance, methods for determining fire resistance of concrete and steel load-bearing elements and different enclosing structures and features of modern structures in fire, and recommendations are given for determining the required fire resistance of structural components [2].

• V . G. Olimpiev, N. F. Gavrikov, S. V. Davydov, etc. engaged in developing the main provisions of calculating the fire resistance of steel and reinforced concrete structures that meet the requirements of building codes and regulations II-B.1-62, building codes and regulations II-A.5-62 and CH 295-64. Including the calculation of the duration of heating and assessment of the stress-strain state of reinforced concrete slabs under non-stationary high-temperature exposure and methods for calculating the fire resistance of bent elements in regular and inclined sections [2].

O.Peterson, S. Magnusson, J. Theor presented a handbook about rational fire engineering design process for loadbearing structures and partitions of steel based on performance requirements. The design methods are based on the rules, advisory notes and recommendations given in the Swedish Building Regulations and in a separate publication on the rational design of fire-fighting equipment, which was compiled based on the instructions of the National Swedish Council for Physical Planning and Construction. The methods presented in this handbook have been given the general approval of the Board (General Approval Certificate No 2698/73) [3].

The study aims to develop a methodology for determining the critical stability parameters of core metal structures, taking into account the emergency associated with heating in the event of a fire.

To achieve this goal, it is necessary to solve the following tasks:

• -    to investigate the influence of the heating temperature of the gaseous medium on mechanical characteristics of steel structures;

• -    to investigate the effect of temperature during uniform heating during a fire on the value of critical stability parameters of metal structures;

• -    to investigate the effect of temperature during uneven heating during fire time per value of critical stability parameters statically indefinable systems made of metal, taking into account cramped working conditions elements and their influence on each other.

2.    Materials and Methods

Influence of an emergency in a standard fire on the critical stability parameters of steel structures. The heating of structures can occur at various temperature conditions of a fire, which reflect a generalized mode of fire development, adapted to the operating conditions of different building materials, products and structures. The nominal dependencies include the standard fire development temperature regime, smoldering temperature regime, outdoor fire temperature regime, and hydrocarbon fire regime. The standard (cellulose) fire curve develops following the accepted scheme. Dependency (1) was derived and published by Russian state standard GOST 30247.0-94 «Elements of building constructions. Fireresistance test methods. General requirements» [4]:

e g = 20 + 345 • lg(8 • t + 1) ,                                       (1)

0 is the ambient gas temperature in the test furnace (°C);

t is the time elapsed since the start of the test (min).

The external fire curve is used in determining the fire resistance limit of the external walls of buildings:

e g = 660 • (1 - 0.687 • e ^{( - 0} .3 ² t ) - 0.313 • e ⁽"'³⁸е ) ) + 20 ,                          ⁽²⁾

The hydrocarbon temperature regime must be used when determining the fire resistance limit of building structures at oil industry facilities:

e g = 1080 • (1 - 0.325 • e ^(-(И67 t ) - 0.675 - e ( " 2⁵t ) ) + 20                          ⁽³⁾

The heating temperature during a fire has a significant effect on steel's strength and mechanical properties.

Table 2.1 shows the values of the reduction factors for the graph of deformation of carbon steel at elevated temperatures. The reduction factors are defined as follows:

KE,e is reduction factor (relative to Ee for an inclined linear section of the elastic deformation area:

к - E K E ^e = E

The value of the coefficients for intermediate temperatures is determined by linear interpolation.

Table 1. Reduction of steel deformation moduli depending on the ambient temperature in case of fire and time

Reducing factor, ^ E,e	Ambient gas temperature, 6g	Time
1	0	0
1	108	0.1
0.9	200	0.29
0.8	300	0.685
0.7	404	1.5
0.6	500	3
0.31	600	6
0.13	700	11.4
0.09	800	22.7
0.0675	900	44.5
0.045	1000	87
0.0225	1010	92
0	1225	390

The influence of the time counted from the onset of a fire on the value of the deformation modulus is shown in Figure 1.

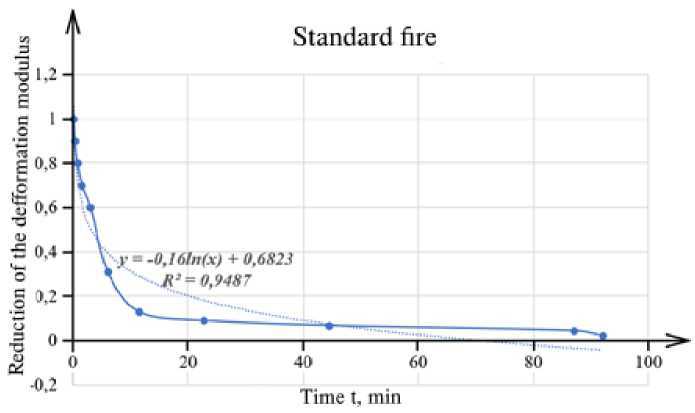
Fig. 1 Influence of the time counted from the beginning of the fire on the value of the deformation modulus

Based on the construction of a trend line with approximation reliability of 94.87%, the dependence of the deformation modulus on time, counted from the onset of standard fire, was obtained:

E _e =- 0.16 • ln t + 0.6823                                        (5)

An important issue in solving the stability problems of structural systems in the event of an emergency during a fire is to identify the most dangerous elements or parts of the structure with low resistance to buckling. [4-6]. Therefore, the study of stability begins with the entire structural system, i.e. from the construction of the calculation scheme, the so-called first level. Using this scheme, a computational analysis of the stress state of all elements is carried out, which are subject to in-depth study in the future.

Let us consider a single-span frame in which the left post is loaded with a force of 4P. The right position is loaded with a force P (Fig. 2) and determines the critical force change during a standard fire and uniform heating of the elements.

Solodilova, V.; Dubrakova, K.; Bulgakov, A.; Erofeev, V.; Otto, J.

Fire resistance of statically indeterminate steel systems;

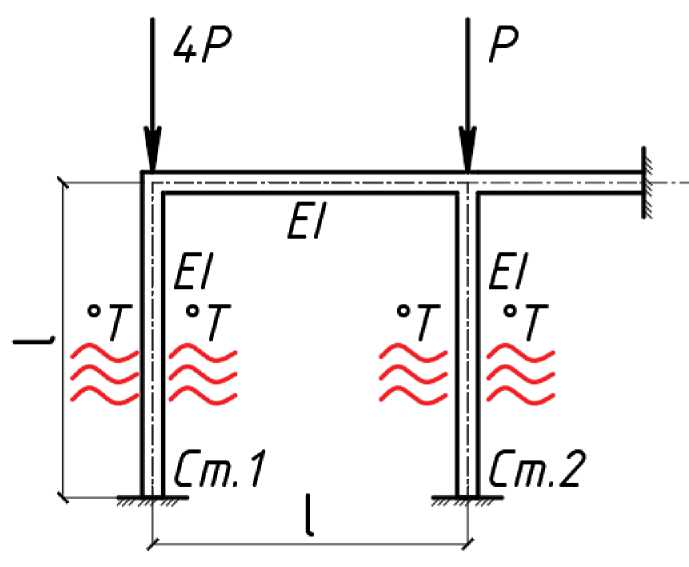
Fig. 2 Design scheme of the frame (made by the authors)

Let us choose the basic system of the displacement method, taking into account its kinematic definability. The loss of stability of the rod is characterized by the appearance of both bending and torsion [7-9].

Applying single angular displacements and constructing bending moment diagrams in an equivalent system, we determine the unknown variables r by the method of cutting nodes and compose

a system of equations for the displacement method:

/ r ii ■ z i + r i2 • z 2 = 0;

_ ^r 12 ■ z i + r 22 • z 2 = 0.

The determinant of a system (6) is determined from the expression:

(4 ■ i ■ ( ^ 2 ( 6 )) + 1) • (4 ■ i ■ (^( 5 2 ) + 2) - (2 ■ i )² = 0

Having calculated the unknown reactions of the supports and found the work of the internal forces of each of the racks of the frame before the fire, we determine the critical force and the type of bifurcation of the elements. If the specified work is negative A i ( M i Q i ) <  0 element buckles actively if A i ( M i Q i ) >  0 – passively [10-12].

After transformations, expression (7) will take the form:

4 ■ (^( 6 )) + 1) ■ M W + 2) - 1 = 0                            (8)

Parameter 6 1 = l ■

4 F EI

Therefore, Э 2 = 2 W .Let us determine the parameters

9 1 and 9 2 for which the determinant of system (6) is equal to 0.

According to the calculation results, the determinant of a system (6) is equal to zero at

^ 2 ( 6 ) = 0.527 and ^ ₂( 6 2 ) = 0.2635 . Therefore, the critical force for rack 1 is Р кр1 =

26.56 ■ EI l2

, for

rack 2 - P = кр ,

7.023 ■ EI l2

. The work of rack 1 is:

A i = 4 ■ i ■ ( ^ 2 ( 6 )) ■ Z i = 0 , A 2 = 4 ■ i ■ ( ^ 2 ( 6 2 )) ■ Z 2 = 0 .

Therefore, A 1 = - 9.997 ■ i , A ₂ = 2.498 ■ i , i.e the first rack before the start of a fire loses stability actively, involving the entire system as a whole in a common bifurcation.

After an emergency associated with a standard fire, with uniform combustion and, accordingly, with uniform heating of the elements [13-14].

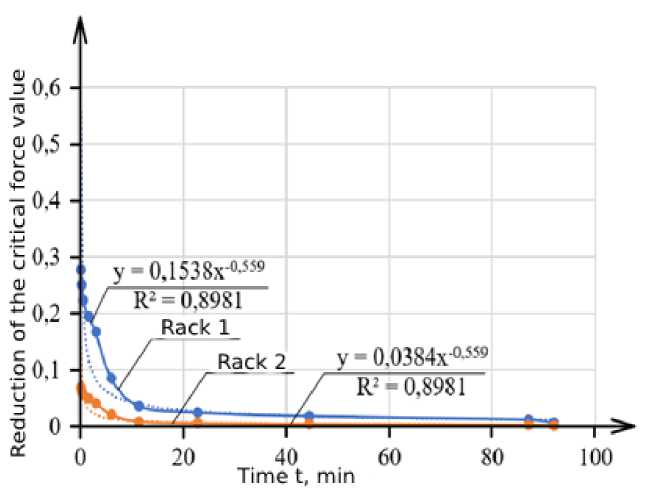
Fig. 3 - Influence of time from the moment of ignition on the value of the critical force for the first and second racks

The critical force will decrease exponentially for both stoics at the same rate. The effect of time from the moment of ignition on the value of the critical force for the first and second racks of the system under consideration is shown in fig. 3

Based on the construction of trend lines with an approximation reliability of 89.81%, the dependence of the critical force on time counted from the onset of a standard fire was obtained

P^ != 0.158 • t ^{( - 0,559)}.                                                ⁽⁹⁾

кр .,1

P_{D 2} = 0.0384 • t ⁽ - ° ^,559).                                           ⁽¹⁰⁾

кр .,2

Consider the situation of a local standard fire, in which only one (second) rack is heated. In this case, the mechanical parameters of one of the racks change, affecting the second one due to cramped working conditions [15-16].

3.    Results and Discussion

At the temperature Т=1112⁰С, t=183 min, the steel deformation modulus of the second (heated) rack will decrease by 64 times, therefore: 6 = 4 • 6 2 . The determinant of the system is determined from expression (6).

According to the results of calculating the determinants of the system, the determinant of system (6) is equal to zero at 6 1 = 1.405 and 6 2 = 0.3 5125 . С Therefore, the critical force for rack 1 is

_D _ 1.97 • EI                    0.123 • EI

.

^Ркр ,1      ^2     ^{, for rack} 2- ^Ркр ,1        2

Consequently, heating the second rack leads to the critical force of the first sharply decreasing: when the second rack is heated to a temperature of 1112.00, the critical force for the first rack will reduce by 13.5 times [17-19].

.At a temperature of T=985⁰С, t=78 min, the steel deformation modulus of the second (heated) rack will decrease by 20.08 times, therefore, for the frame under consideration: 6 1 = 2.24 6 2 . The determinant of a system (6) is determined from expression (7).

According to the results of calculating the determinants of the system, the determinant of a system

6.3 ⋅ EI l ²

• (6)    is equal to zero for ϑ ₁ = 2.51 and ϑ ₂ = 1.12 . Therefore, the critical force for rack 1 is P_{кр ,1} =

7.09 ⋅ EI

1.25 ⋅ EI for rack 2 - P =         .

кр ,2        _l 2

The critical force of the first strut under local fire impact at Т=9850С on the second strut decreases by 4.2 times.

At the temperature Т=960⁰С, t=66 min, the steel deformation modulus of the second (heated) rack will decrease by 17 times, therefore, for the frame in question: ϑ ₁ = 2.108 ⋅ ϑ ₂ . The determinant of a system (6) is determined from expression (7).

According to the results of calculating the determinants of the system, the determinant of a system (6) is equal to zero at ϑ ₁ = 2.663 and ϑ ₂ = 1.263 . Therefore, the critical force for rack 1 is

1.595 ⋅ EI

l ²

P_{кр ,1} =      ₂     , for rack 2 - P_{кр ,2}

The critical force of the first strut under local impact at Т=9600С of fire on the second strut decreases by 3.75 times.

At the temperature Т=633.30С, t=7.8 min, the steel deformation modulus of the second (heated)

rack will decrease by 4 times, therefore: ϑ1=ϑ2. The determinant of the system is determined from expression (6). According to the results of calculating the determinants of the system, the determinant of a system (6) is equal to zero at ϑ1 = 3.05 and ϑ2 = 3.05 . Therefore, the critical force for rack 1 is

9.303 ⋅ EI                     9.303 ⋅ EI

.

P_{кр ,1} =      ₂      , for rack 2 - P_{кр ,2} =      ₂

Consequently, heating the second rack leads to the fact that the critical force of the second one decreases: when the second rack is heated to a temperature of 633.00, the critical force for the first rack decreases by 2.85 times [20-22].

At the temperature Т=4040С, t=1,5 min, the steel deformation modulus of the second (heated) rack will decrease by 1.43 times, therefore: ϑ1 = 0.5975⋅ϑ2. The determinant of the system is determined from expression (6).

According to the results of calculating the determinants of the system, the determinant of a system

• (6)    is equal to zero at ϑ ₁ = 5.28 and ϑ ₂ = 3.1548 . Therefore, the critical force for rack 1 is

27.88 ⋅ EI                    9.95 ⋅ EI

.

P_{кр ,1} =            , for rack 2- P_{кр ,2} =

^,             l ^{2                                  ,}            l ²

The critical force of the first strut under local fire impact on the second strut increases by 1.05 times.

Figure 4 shows the dependence of the critical force of the first strut when a standard fire acts on the second strut. The work of rack 1 is equal to: A ₁ = 4 ⋅ i ⋅ ( ϕ ₂ ( ϑ ₁)) ⋅ Z ₁ , A ₂ = 4 ⋅ i ⋅ ( ϕ ₂( ϑ ₂)) ⋅ Z ₂ . Therefore,

A ₁ = - 9.997 ⋅ i , A ₂ = 2.498 ⋅ i , those the first rack before the start of a fire loses stability actively, involving the entire system as a whole in a common bifurcation.

Change in the critical force of the first rack under local fire impact on the second y = -6E-10x4 + 2E-06x3 - 0.0014x2 + 0.4406x - 6.2849

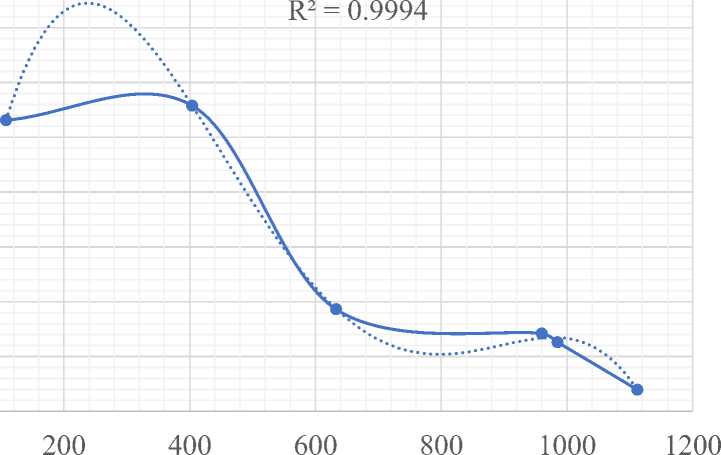
Fig.4 - Dependence of the critical force of the first column when exposed to a standard fire on the second column

Based on the construction of trend lines with approximation reliability of 99.94%, the dependence of the critical force of the first prop on temperature the impact on the second prop during a standard fire was obtained:

Р кр 1 = - 6 E - 10 Т ⁴ + 2 E - 06 Т ³ - 0.0014 Т ² + 0.4406 Т - 6.2849 ⁽¹¹⁾

From the dependence shown in Figure 4, it can be seen that at a fire impact temperature on the second rack up to 4300C, the critical force of the first rack grows, increasing by an average of 5%. With an increase in the temperature of the impact on the right element over 4300, the critical force of the first rack sharply decreases in proportion to the increase in the temperature of the effect [23-24].

The work of rack 1 is equal to: A 1 = 4 ■ i • ( ^ ₂( ^ 1 )) • Z 1 , A ₂ = 4 • i • ( ^ 2 ( ^ 2 )) • Z 2 • Therefore, at a temperature 430 0 С, A 1 = 1.84 • i , A 2 = - 0.531 ■ i , those. The first fire leg loses its stability passively, and the second one actively, involving the whole system in the general bifurcation.

It has been determined that at a fire impact temperature on the second strut up to 4300C, the critical force of the first strut grows, increasing by an average of 5%. With an increase in the temperature of the impact on the right element over 4300С, the critical force of the first rack sharply decreases in proportion to the increase in the temperature of the impact. These changes are because at the heating temperature of the second rack in the range from 0 to 4100C, the first rack loses stability actively. When the impact temperature of 4100С on the right rack is exceeded, the left transition to a passive bifurcation [25,26].

4.    Conclusions

An emergency that has arisen during a standard fire has a significant impact on the critical parameters of the stability of steel structures. Out-of-design impacts, accompanied by a sudden change in geometry cause changes in critical parameters and their corresponding values of critical forces.

• 1.    The nominal dependencies include the standard fire development temperature regime, smoldering temperature regime, outdoor fire temperature regime, and hydrocarbon fire regime. The curve of various fires is taken according to the accepted regularity.

• 2.    Based on the statistical data, the dependence of the decrease in the deformation modulus of steel due to temperature increase was revealed and converted into a variable curve.

• 3.    An important issue in solving the stability of structural systems in the event of an emergency during a fire is to identify the most dangerous elements or parts of a structure with low resistance to buckling. Having chosen the main system of the displacement method, taking into account its kinematic determinability, we calculated that before a fire occurs, the first strut will begin to lose stability actively, involving the entire system as a whole in a common bifurcation. with uniform heating of the elements, the critical force will decrease exponentially for both racks at the same rate. Considering the situation of a local standard fire, only one (second) rack is heated. The dependence of the critical force of the first rack when a standard fire affects the second rack was revealed. It has been determined that at a temperature of fire impact on structures up to 430⁰C, the critical force of one of the bearing elements increases by an average of 5%. With an increase in the impact temperature on the second element over 430⁰C, the critical force of the first element sharply decreases in proportion to the increase in the impact temperature.