Физическая модель электродуговой зоны в плазменном реакторе совмещенного типа

Значение ископаемых углей как источника энергии и сырья для промышленности все более возрастает. Особое внимание уделяется бурым углям, добыча которых постоянно увеличивается. Они рассматриваются не только как энергетическое топливо, но также как сырье для химикотехнологической переработки. Однако такие угли отличаются высоким содержанием влаги, характеризуются пониженной теплотой сгорания, при хранении на воздухе разрушаются. Для устранения данных недостатков используются методы деструктивно-термической переработки, позволяющие получать из бурых углей высококачественную продукцию, необходимую для использования в промышленности. Основой процесса получения целевой продукции из угля при любом его техническом оформлении является термодеструкция [1].

В качестве нового способа обработки бурых углей и получения угольных сорбентов возможно использование низкотемпературной плазмы, которая значительно повышает эффективность переработки и активации углей за счет интенсификации процессов пиролиза, протекающих под действием высокой температуры и большой удельной мощности, а также из-за высокой концентрации активных радикалов, ионов и электронов [2]. Для исследования процессов газификации и пиролиза углей была создана универсальная плазменная модульная установка совмещенного типа (рис. 1), которая открывает возможность комплексного подхода к получению активированного угля и синтез-газа.

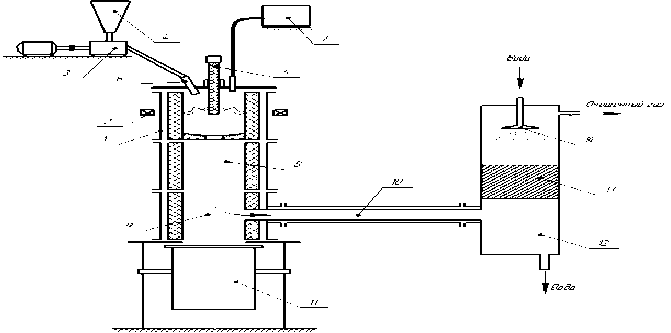
Рис. 1. Плазменный модульный реактор совмещенного типа. 1 – реактор; 2 – магнитная катушка; 3 – дозатор; 4 – бункер сырья; 5 – катод; 6 – эжектор; 7 – парогенератор; 8 – камера муфеля; 9 – камера разделения; 10 – труба вывода газа; 11 – сборник твердого остатка; 12 – скруббер; 13 – фильтр; 14 – ороситель

Применение модульного принципа позволяет упростить конструкцию, облегчить ремонт и эксплуатацию оборудования, уменьшить энерго- и металлозатраты.

Реагенты (угольная дробленка, пар) поступают сверху через крышку реактора в межэлектродный промежуток, где дуга постоянного тока вращается с помощью внешней электромагнитной катушки. Проходя через высокотемпературную электродуговую зону (рис. 2), реагенты вступают в реакцию. В результате реакции пароводяной газификации образуется синтез-газ, состоящий преимущественно из СО (угарного газа) и Н 2 (водорода). Крупный твердый остаток падает в бункер пиролиза и активации, а мелкодисперсные частицы вместе с синтез-газом «засасываются» в скруббер, где и происходит их улавливание.

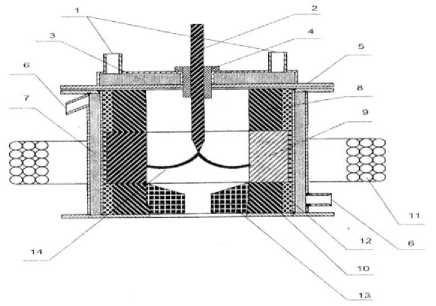
Рис. 2. Электродуговая камера плазменного реактора. 1 – ввод и вывод охлаждающей воды в крышке плазменного реактора; 2 – графитовый стержень (катод); 3 – охлаждающая вода; 4 – изолятор; 5 – крышка плазменного реактора; 6 – ввод и вывод охлаждающей воды плазменного реактора; 7 – охлаждающая вода; 8 – верхнее графитовое кольцо; 9 – анодное графитовое кольцо; 10 – нижнее графитовое кольцо с выемкой для установки диафрагмы; 11 – соленоид; 12 – графитовая крошка; 13 – графитовая диафрагма; 14 – электрическая дуга

В эксперименте использовался уголь, размеры фракций которого составляли после просеивания от 0,1 до 1 мм. Уголь пропускается через плазмохимический реактор с вращающейся магнитным полем дугой. При равномерном вращении анодного пятна дуги между кольцевым катодом в реакторе образуется сплошная плазменная среда со средней температурой 2500-3000 K. За счет этого подаваемые сверху в реактор частицы угля полностью проходят термохимическую обработку плазмой. Время пребывания частиц угля в плазменной зоне зависит от размера фракции, регулируется установкой диафрагмы в нижней части плазменного реактора и составляет от 0,1 до 1 с.

В электродуговой зоне реактора описываемого типа вводимая в камеру электрическая мощность в электрической дуге превращается в тепловую. Таким образом, электродуговая зона является зоной генерирования тепловой энергии, ее поглощения, она перекрывает все сечение камеры, позволяет регулировать время пребывания в ней угольной пыли, концентрацию мощности и, следовательно, температуру. Эта зона по высоте ограничена плоскостями, перпендикулярными оси камеры и проходящими через конец электрода (верхняя) и через середину электромагнитной катушки-соленоида (нижняя). Тепловая энергия генерируется в зоне вращающейся дугой и под влиянием течений газа, получающегося при термическом воздействии на угольную пыль, распределяется по всему ее объему.

Мощность зоны генерирования определяется условием равномерного ее распределения. Для этого используется формула мощности постоянного тока:

P р = U р ⋅ I р ,                                                    (1)

где: P р – мощность реактора; U р и I р – соответственно напряжение и сила тока реактора. В экспериментах по термической обработке углей использовались следующие значения напряжения и силы тока: U р = 200 В; I р = 200 А.

В расчетах диаметр камеры реактора принимается за определяющий размер, и все основные закономерности электродуговой зоны выражаются через него. Это дает возможность распространить результаты эксперимента, полученные на реакторах малой мощности, на геометрически подобные реакторы большой мощности и, следовательно, больших диаметров камеры. Ток реактора I р выражается через плотность тока, отнесенную к площади сечения камеры:

I р = ∆i p πД к ²/4.                                              (2)

Соответственно, плотность тока ∆i p = 4 I р / πД к ² = 1,132 А/см².

Напряжение реактора U р представляется через градиент напряжения межэлектродного промежутка:

U р = E p Д к /2.                                             (3)

Здесь Д к /2 – межэлектродный промежуток, к которому относят напряжение дуги для определения градиента напряжения (при реакторе со стержневым катодом).

Соответственно градиент напряжения E p = 2 U р /Д к = 26,7 В/см. В итоге с учетом выражений для I р и U р выводится формула для мощности реактора:

P р = U р ⋅ I р = π/4 ⋅ 1/2 E p ∆i p Д к ³ ≈ 0,39 E p ∆i p Д к ³,                          (4)

которая равна: P р ≈ 0,39 E p ∆i p Д к ³ = 0,39 ⋅ 26,7 В/см ⋅ 1,132 А/см² ⋅ (15)³ см³ = 40 кВА = 40 кВт.

В результате преобразований делается вывод, что выделяемая в объеме зоны генерирования тепловая мощность, равная вводимой электрической мощности, пропорциональна кубу диаметра камеры, она же пропорциональна плотности тока ∆i_p и градиенту напряжения E_p или иначе объемной мощности W _p, выделяемой в зоне. Величина W _p, определяющая температурный уровень, является, как очевидно, константой для данного производства на геометрически подобных реакторах:

Wp = const.(5)

Следовательно, можно принять константами ∆i p и E p :

∆ip ≈ const.(6)

Ep ≈ const.(7)

Величину ∆ip ≡ Iд/Дк2 определяют с помощью горячих моделей [3] из условий высоких технологических показателей при высокой производительности установки. Затем при заданном диаметре реактора ее величину обеспечивают выбором тока. Из изложенного следует, что для подобия тепловых зон необходимо в качестве константы принять также индукцию внешнего магнитного поля (от электромагнитной катушки) на оси камеры:

B ≈ const.

Естественно, если тепловая мощность реактора изменяется пропорционально кубу его диаметра, то, соответственно, перерабатываемый материал (уголь) при постоянстве энергии, необходимой на единицу массы, нужно подавать в него пропорционально кубу диаметра с учетом КПД:

G _час = P р η_т/m,

где: G час – часовая загрузка угля, кг; η т – термический КПД; m – расход энергии на обработку 1 кг угля.

Зависимость E p ≈ const при B ≈ const, I д /Д к ² ≈ const и выходе газа, пропорциональном Д к ³, подтверждена экспериментально для камер диаметром 10, 15 и 20 см (рис. 3) [4]. При Д к , равном 15 и 20 см, градиенты напряжения практически совпадают: при Д к = 10 см E p 10 см больше E p 15 см и E p 20 см . В последнем случае, видимо, сказывается повышенное охлаждающее действие стенок при малом диаметре камеры, а также нелинейность вольтамперных характеристик. В соответствии с этим делается заключение, что камеры слишком малого диаметра непригодны для моделирования.

Зная величину констант (5–8) для данного процесса с учетом формулы (7), а также расхода энергии на обработку 1 т угля, можно определить диаметр камеры геометрически подобного реактора и другие его размеры при различных мощностях или производительности по углеобработке [5].

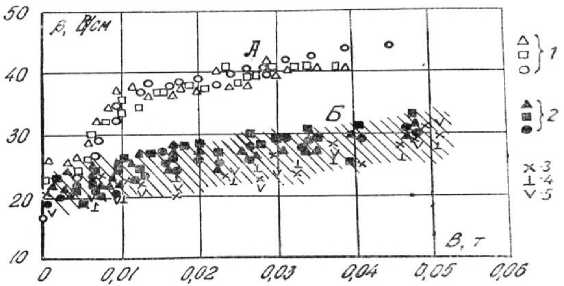
Рис. 3. График изменения зависимости E_p = f(B) в камерах диаметром 10 см (кривая А), 15 и 20 см (кривая Б; залитые точки соответствуют диаметру 15 см, фигурные – диаметру 20 см)

Далее находится скорость движения дуги по кольцевому электроду, учитывая при этом, что в реакторах для подобия тепловых зон сохраняются одинаковыми плотность тока в сечении камеры I д /Д к ² ≈ const и индукция магнитного поля B ≈ const. Из равенства газодинамических сил сопротивления движению [4] и электромагнитных движущих (на единицу длины) имеем:

B ⋅ I д ~ ( s ⋅ v окр ² ⋅ c ⋅ ρ)/2g,

где: s – миделево сечение дуги; v окр – скорость ее движения по кольцевому электроду; ρ – весовая плотность среды; c – безразмерный коэффициент; g – ускорение силы тяжести. Отношение ρ/2g для данной среды и при заданной температуре ее нагрева можно принять постоянным. Далее считаем cs эквивалентным миделевым сечением s _экв. Тогда на основании равенства (1.10) получается:

v _окр ~ ( B ⋅ I _д/ s _экв)

Поскольку I д ~ Д к ², B ≈ const и s экв ≈ const, то окончательно имеем:

v окр ~ Д к .

В электродуговом реакторе скорость движения дуги по кольцевому электроду (аноду) при B ≈ const и I д ~ Д к ² примерно пропорциональна диаметру камеры Д к или, что тоже самое, во всех геометрически подобных реакторах электрические дуги вращаются с примерно постоянными угловыми скоростями. Это одно из условий подобия тепловых зон. В исследуемом реакторе производительность по обработке угля пропорциональна примерно кубу диаметра камеры. Необходимо определить, как зависит кинетическая энергия струй, несущая способность, от диаметра камеры. Для этого необходимо воспользоваться формулой:

Σ^l 0 1/2 ρ ⋅ v ² = I д ⋅ Σ^l 0 ∆i pазн l ед ,                                                  (12)

учитывая, что плотность тока электродных пятен дуг достаточно большой силы тока, находящихся в одних и тех же условиях, с изменениями тока меняется незначительно [6]. Используя зависимость миделева сечения от тока и напряженности магнитного поля, необходимо исходить из модели «обдуваемой» дуги, при которой она представляется сплюснутой с лобовым (к движению) размером сечения, постоянным при изменениях тока. Ввиду того, что ток дуги в реакторе выбран пропорциональным Д к ², при постоянном лобовом размере размер ее сечения, перпендикулярный лобовому, при сохранении прочих условий должен быть пропорциональным Д_к², а плотность тока в сечении дуги оставаться неизменной. Дуга у кольцевого электрода, где скорость ее вращения максимальна, имеет заметное расширение [7]. Оно возрастает с увеличением Д к и соответственно тока, так как при этом согласно формуле (11) повышается и скорость дуги – изменяются условия ее существования. Перпендикулярный лобовому размер столба растет при этом быстрее, чем Д к ². Поскольку v окр ~ Д к , то соответственно с ростом Д к и тока будет увеличиваться перпендикулярный лобовому размер сечения дуги Д к ² и пропорционально снижаться плотность тока у кольцевого электрода. На стержневом электроде (катоде) плотность тока в пятне значительно не изменяется, так как условия его существования здесь при этом не претерпевают изменений. В связи с ростом разности плотностей тока на стержневом и кольцевом электродах растут как струйные течения, так и несущая способность дуги [8]. Следовательно, для плазменного реактора имеется следующее соотношение:

Σ^l 0 ∆i pазн l ед = ( ∆i max – ∆i min ) ~ Д к .                                  (13)

Формула (12) для данного случая и для однотипных реакторов с изменением диаметра камер может быть записана в виде:

Σ^l 0 1/2 ρ ⋅ v ² ≈ I д Σ^l 0 ∆i pазн l ед ~ Д к ³.                                         (14)

В приведенных формулах ∆i max и ∆i min – плотности тока на концах дуги. Несущая способность дуг (кинетическая энергия струй) так же, как и производительность при обработке угля, пропорциональна кубу диаметра камеры Д к ³ (при B ≈ const и I д ~ Д к ²). Таким образом, получена важная закономерность электродуговой зоны, указывающая пути организации эффективной обработки угля в плазменном реакторе.

Следующим этапом моделирования электродуговой зоны реактора является определение тепловых потерь в электромагнитной катушке (джоулево тепло) с увеличением диаметра камеры реактора. Известно, что магнитная индукция B в центре кругового тока рассчитывается по формуле:

B = μ a I э-м.к / a ,                                                     (15)

где: μ a – абсолютная магнитная проницаемость вещества; a – радиус реактора; I э-м.к – ток катушки.

Магнитная индукция в опытах при Iэ-м.к = 50 А составила B =0,001 Тл. Из приведенной формулы вытекает, что при сохранении величины магнитной индукции на оси реактора неизменной ток в катушке должен возрастать пропорционально увеличению диаметра камеры реактора (2a = Дк). Соответственно, джоулевы потери мощности будут пропорциональны произведению квадрата тока катушки на электрическое сопротивление ее витков. При увеличении диаметра катушки (Дк = 2a) растут длина ее обмотки и сопротивление, но при этом вследствие повышения тока увеличивается сечение обмотки и сопротивление падает, поэтому результирующее сопротивление катушки не изменяет- ся. Тепловая мощность будет повышаться пропорционально Дк2, и относительные потери в электромагнитной катушке (Pкат./Pреакт.) с ростом мощности реактора и его диаметра будут уменьшаться [3, 5]. Если же с ростом диаметра камеры реактора будет увеличиваться и магнитная индукция, то при этом потери мощности в катушке возрастут пропорционально Дк3, а относительные потери останутся неизменными (~1%). Следовательно, магнитные поля можно применять для управления термическими зонами реактора [7, 9].

В электродуговой зоне при B ≈ const и I д ~ Д к ² силы, движущие дугу вокруг анода F = BI д , пропорциональны Д к ², им равны и силы сопротивления движению F сопр. ~ Д к ², и сила упругости F упр. ~ I д ~ Д к ². Но поскольку интенсивность закручивания дуг определяется этими же силами и все они изменяются одинаково при изменении диаметра камеры, то можно считать, что при этих условиях закру-ченность дуговых столбов с изменением Д_к остается постоянной.

Из вышесказанного следует важный вывод: в дуговых реакторах совмещенного типа при B ≈ const и I д / Д к ² ≈ const число витков закручивания дуг не изменяется:

ω ≈ const                                               (16)