Физическая модель термоусадки синтетической модифицированной полиолефиновой нити с эффектом памяти формы на основе кластерных представлений

Возрастающее количество электронных элементов в текстильной, автомобильной и других видах промышленности требует дополнительных мер по обеспечению электроизоляции, защиты устройств от вредного воздействия окружающей среды и химических веществ

[1-2].Одной из широко используемых и оправданных с экономической точки зрения технологий для изоляции и герметизации проводки, защиты мест соединений проводов и различных элементов электрооборудования стало применение термоусаживаемых материалов в виде трубок, в том числе из технического текстиля.

Это современный простой в применении высокотехнологичный материал, нашедший широкое применение в электротехнике, энергетике, автомобилестроении, авиастроении, приборостроении. Основным компонентом текстильных термоусаживаемых трубок является полиолефиновая нить с эффектом памяти формы, исследование которой представляет большой научный и практический интерес.Целью работы является построение физической модели процесса термоусадки полиэтиленовой нити с эффектом памяти формы и оценка ее энергетических состояний.

Образцы и методы исследования

Объектом исследования является полиэтиленовая нить с эффектом памяти формы. Данная нить является основным термоусаживаемым компонентом текстильного полотна полотняного переплетения InnoSHRINK XTFS. диаметром 10 см .

Для формирования эффекта памяти формы полиэтиленовую нить необходимо подвергнуть модификации в несколько этапов. Сначала нить подвергают радиационной сшивке, после чего при температуре, близкой к температуре плавления, подвергают процессу ориентационной вытяжки [3 – 8]. Из данных по термической усадке [6, 8 – 9] следует, что коэффициент вытяжки полиэтиленовой нити с эффектом памяти формы λ=8. После процесса вытяжки нить охлаждают до комнатной температуры.

Опыты по термоусадке проводились в интервале температур 115÷200 ⁰ С [6]. Для каждой температуры процесс усадки под действием температуры полиэтиленовой нити с эффектом памяти формы можно представить в виде:

S = « нас (1 - e"^в ) ,       (1)

l-l где S =--усадканити;/0- начальная длина lо нити;l – длина нити после усадки; ε – максимальновозможная усадка при выбранной температуре.

Коэффициент β обратно пропорционален времени релаксации τ , характеризующем время перехода через потенциальный барьер. Коэффициент β был определен экспериментально. На рисунке 1 представлена зависимость коэффициента β от температуры воздействия.

Современные представления о структуре полимерных материалов [10 – 14] позволяют предложить физическую модель, описываю- щую процесс термической усадки полиолефиновой модифицированной нити с эффектом памяти формы. Разобьем структуру полимерной нити на множество отдельных групп макромолекул, соединенных сшивками, которые впоследствии будем называть кластерами. Представления о кластерной структуре предложены в работах [15 – 16]. Для описания процесса восстановления формы полимерной нити с эффектом памяти формы обычно используют упрощенные феноменологические модели [17].

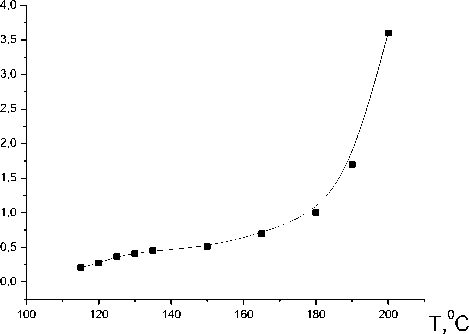
Рисунок 1 – Зависимость коэффициента β от времени теплового воздействия

Различные модели основываются на концепции одного или нескольких потенциальных барьеров. Применим к исследуемой полиэтиленовой нити с эффектом памяти формы модель двух состояний, т.е. кластер может находиться либо в вытянутом состоянии с энергией U 3 , либо в сжатом c энергией U 1 . На рисунке 2 представлена зависимость энергии кластера от степени его растяжения.

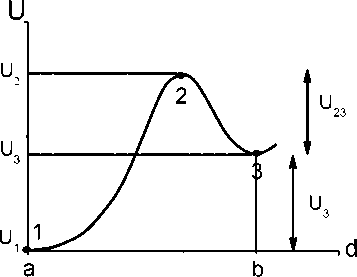
Рисунок 2 – Зависимостьэнергии кластера от степени его растяжения

Участок кривой 1 – 2соответствует тех-

нологическому процессу вытяжки нити при температуре, близкой к температуре плавления на стадии производства нити с эффектом памяти формы. До своего растяжения кластеры находятся в состоянии с энергией U 1 . Участок кривой 2 – 3характеризует процесс при охлаждении вытянутой нити на стадии производства. Кластеры переходят в квазиравновесное состояние с энергией U 3 . Таким образом, происходит ”замораживание” элементарных объемов - кластеров в квазиравновесном состоянии U 3 . С энергетической точки зрения, эффект памяти формы заключается в том, что состояние c энергией U ₁ более энергетически выгодное, чем состояние с энергией U ₃.

Вероятность перехода кластера через потенциальный барьер можно представить в виде:

кДж

Получаем U 23 =65÷68       ,

моль

или около

7800 К . Таким образом, мы имеем дело с “высокими” потенциальными барьерами.

Для оценки U 2 и U 3 применим общее уравнение деформации, выведенное ранее и представленное в работе [23]. Приведем конеч-

ное уравнение:

d                         *2^

— (a - £  ) + (a - £  )(eY упр + e 3

dk^{v w})  ^{( w)(}

*  2

■ Y ^£ упр ) =

... = x sh⁽ Y ^£ Упр ), ⁽⁴⁾

где величины со значком ” * ” представляют собой приведенные величины, т.е. величины, отнесенные к величине ( kT ), где: k =

1,38 - 10 ^{- 23}

Дж

– постоянная Больцмана; γ

К ⋅ моль

- ^U 12 kT

13     ^v 0 e     ;

- ^U 23

kT

31 ^v 0 e     ,

– коэффициент, зависящий от рода нити, имеющий размерность Дж; это поправка к энергиям, необходимым для преодоления потенциального барьера, которую требуется учесть при приложении к нити внешнего меха-

где ν – коэффициентпропорциональности, с^-1.

Оценим энергию активации U 23 . Кинетические (активационные) характеристики при

нического воздействия; sh(у*£ ² ) =

. *2

Y eγ εx

-e

. *2 - Y £ x

– гиперболический синус величины γε ;

термоусадке полимеров определяются трансгош переходами в сегментах макромолекул [1820]. Известно, что кинетические характеристики кооперативных конформационных переходов в полиэтилене имеют следующие значения: Е 0 =30÷70 кДж/моль ; предэкспоненциальный множитель – К 0 =10^-6÷ 10^-7 [18 – 22]. Такая величина Е 0 объясняется тем, что изменение размеров полимеров (деформация ползучести, усадка и прочее изменение размеров) связано не с одиночными гош-транс и транс-гош переходами (энергия активации которых для ПЭ равна 12÷15 кДж/моль ), а с несколькими конформационными переходами в элементарных сегментах макромолекул.

Проведем оценку энергии активации процесса термоусадки мононити из сшитого полиэтилена на основе экспериментальных данных, полученных в работе [6].

U ₂₃= RT In - , (3)

t 0

Дж где:R=8, 31         ;T – температура, К;t

– вре-

мя выхода усадки в режим стабилизации; t ₀=10^-6c.

^X f ( T )

² mn 5   _

---_:--безразмерный параметр, яв- e ^{- U 3} + 1

ляющийся функцией температуры; δ = b - a – единичный квант деформации элементарного N объема макромолекул; m =   – линейная

L 0

плотность элементарных объемов макромолекул; L - первоначальная длина образца; N - число элементарных объемов;t – время тепло-

1      *

вого воздействия; 0  = — eU 12; k =---; v0 - p   v 0

коэффициент, имеющий размерность с-1;

σ

ε =    – упругая часть деформации;

X

Применяя уравнение (3) в режиме термоусадки с начальными условиями, характерными для нагревания нити в свободном состоянии, £ _упр = 0 , получим уравнение в частном виде, описывающее процесс термической усадки исследуемой полиолефиновой модифицированной нити.

— + (1 + e * ) e = 0 . dk

Уравнение (5) представляет собой дифференциальное уравнение с разделяющимися

переменными. Его решение

U_n = U ₃ + U ₃ = 90 кДж = 10900 К (7) моль

Оценив значения U23, U3 и U12 , можно получить значение v0 для дальнейшего расчета

£ = ^ нас ⁽¹ - e

d+ eU i ) v ,

•""    )    (6)

совпадает с ранее предложенным уравнением (1) для термической усадки нити.

вероятности перехода за единицу времени элементарных объемов через потенциальный барьер по формуле 2. После подстановки экспериментальных значений коэффициента

Величина

*

(1 + e^U 3 )

Р =

*

(1 + e^{U 3} )

U *2

e ¹²

v₀ представляет со-

U * e ¹²

^V 0

для различных температур бы-

бой коэффициент в в уравнении (1). Подставив экспериментальные значения в для двух

различных температур и исключив v ₀, можно

кДж оценить значение U =25       , что соответст- моль

вует 3000 К. Тогда

ло найдено среднее значение коэффициента v₀ ~ 1 - 10 ⁶ с ^{- 1} . С учетом значения v ₀, оценим вероятности переходов элементарных объемов через потенциальный барьер по формуле (2) На рисунках 3 и 4 представлены зависимости вероятностей энергетических переходов в единицу времени через потенциальный барьер от температуры.

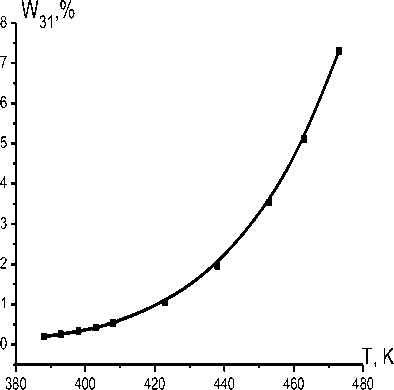
Рисунок 3 – Зависимостьвероятности перехода W ₃₁ в единицу времени через потенциальный барьер в направлении3 – 1

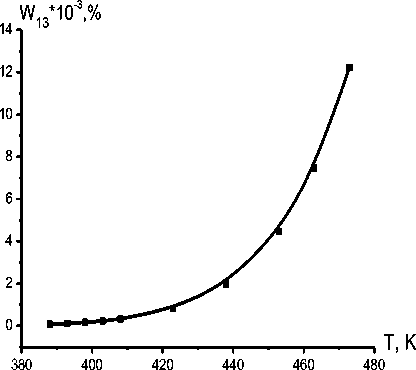
Рисунок 4 – Зависимостьвероятности перехода W13 в единицу времени через потенциальный барьер в направлении1 – 3

Как видно из рисунков 3 и 4, вероятность переходов в единицу времени через потенциальный барьер в направлении 1 – 3 W 13 чрезвычайно мала, так что спонтанный переход кластеров из состояния 1 в состояние 3 даже при повышенных температурах практически исключается.

Таким образом, процесс термоусадки с учетом U 23 , U ₃, U 1 2 и v ₀ можно описать уравнением регрессии вида:

- (1 + e T ^- 60 - 10 ⁶ 1

10,9 - 103

Е = Е нас ⁽¹ — e e T         ) ,           (7)

где t – время, измеряемое в минутах.

Выводы

Предложенная кластерная модель поведения полиолефиновой нити позволяет не только качественно, но и количественно описать эффект «памяти формы», что дает возможность в дальнейшем успешно прогнозировать поведение материалов, в состав которых входят полиолефиновые нити.