Физическая очередь в прикладной теории массового обслуживания

Таким образом, если обычная математическая очередь рассчитывается как среднее по всем заявкам, побывавшим в системе, то очередь без нулевых входов должна рассчитываться как средняя величина за вычетом тех требований, которые были обслужены немедленно, поскольку попали в систему в тот момент, когда, по крайней мере, один из каналов обслуживания был свободен. В соответствии с терминологией, принятой в системе имитационного моделирования GPSS, будем называть нулевым входом такой приход заявки в систему, при котором имеется, по крайней мере, один свободный канал обслуживания, и заявка в этом случае обслуживается немедленно. Назовём физической очередью очередь, рассчитанную без учёта нулевых входов. В случае занятости всех обслуживающих каналов вновь прибывшая в систему очередная заявка будет вынуждена ожидать обслуживания в накопителе, при этом минимальное количество заявок в накопителе равно нулю.

Как и привычная математическая очередь, рассчитываемая с учётом нулевых входов, физическая очередь также характеризуются моментами числа требований, ожидающих обслуживания, и соответственно, моментами времени ожидания обслуживания вновь прибывшей заявкой в соответствующей очереди. Идея расчёта этих моментов заключается в том, что в этом случае при расчёте параметров очереди следует переопределить условие нормировки с учётом только тех состояний СМО, при которых отсутствуют нулевые входы. Говоря другими словами, нужно учесть при расчётах только те состояния системы, в которых присутствует физическая очередь. Таким образом, алгоритм расчёта параметров физической очереди полностью идентичен алгоритму расчёта математической очереди за исключением вероятностей возможных состояний СМО, которые теперь должны рассчитываться исходя из нового условия нормировки, исключающего состояния, соответствующие нулевым входам.

В данной работе в рамках модели наиболее общей системы массового обслуживания с произвольным количеством источников и ограничений по длине очереди [5] получены общие математические выражения для первых и вторых моментов числа требований, ожидающих обслуживания в физической очереди. Также рассчитаны соответствующие функции распределения, и как следствие, первый и второй моменты времени ожидания начала обслуживания заявкой в очереди указанного типа.

Вероятностные характеристики и моменты числа требований в физической очереди. В работе авторов [5] была представлена наиболее общая математическая модель открытой многоканальной СМО, имеющей m обслуживающих устройств одинаковой производительности с экспоненциально распределенным временем обслуживания. Входной поток требований в этом случае является суперпозицией произвольного числа компонент h, каждая из которых представляет собой пуассоновский поток заявок, обслуживаемых в порядке очереди. Для каждого типа требований, поступающих в систему из j-го источника, действует своё ограничение на длину очереди 8j, при этом 80 < 81 < 82 <•< 8h . В настоящей работе мы также будем использовать обозначения, принятые в работе [5]:

8о = E0 = 0; 81 = *; 82 = * + E2V• 8j = ZEi = ZE; -i=0

ограничения длины очереди (объёма накопителя) для заявок j-й компоненты;

hhh

Ло = ZAj; Л1 = ZAj; Л2 = Z^jV"• Лh = Ah; j=0               j=1

где A — интенсивность потока заявок j-й компоненты; ц — интенсивность обслуживания заявок одним обслуживающим устройством;

h hh

R=Zpa R=Zр; R =ZpjV• Rh = ph; Ri=— j=0             j=1             j=2

где P j — приведенная интенсивность потока заявок j-й компоненты.

Для расчёта параметров физической очереди на базе разработанной и представленной в работе [5] универсальной математической модели необходимо переписать условие нормировки таким образом, чтобы при суммировании в этом условии учитывались лишь те состояния системы, которые соответствуют физической очереди. В результате имеем m+8h

Е p = ¹

i = m                            (1)

- условие нормировки для расчёта физической очереди.

Подставив соответствующие выражения для вероятностей стационарных состояний P i в представленное выше условие нормировки, и решая полученное уравнение относительно Р ₀, получим следующее выражение величины Р₀ , используемое для расчета физической очереди:

состояния системы Р₀ , то есть вероятность полного отсутствия заявок в системе, которая в этом расчёте не нужна, а некоторый коэффициент пропорциональности, который может быть и большим единицы. Физический смысл при этом имеют лишь величины вероятностей соответствующих состояний системы P i , которые, конечно, для всех значений i >  m остаются меньшими, чем единица. При этом формулы для остальных вероятностных характеристик, предназначенных для расчёта параметров физической очереди, будут выглядеть точно так же, как и при расчёте характеристик обычной математической очереди с заменой ^Р ₀ на Р ₀ . Имеем

m

R ^p

P 0 , m !

D m    D m h  g ^{- 1} ( —

P0 = R0-+R-Zn — m!   m! g=1 j=01 m

m

\g - I ( — .

I E j

X

m + 8. <  i <  m + 8 ,^ ₁₉   0 <  j <  h - 1

j                   j ^{+ 1}

- вероятности всевозможных состояний СМО в стационарном режиме;

m !

g=1 j=0 V m m — -g

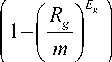
i—1 f p *\Eg mm p =ttI Rg I R^pJ

P Bi   П 1     I     |  0

g = 0 V m J m ^!

m 1

—

- i 1 * 1 m )

m — —

* , R = m

—, — ^ m

. E g ,   ^- g = m

Подчеркнём, что в данном случае P0 пред- ставляет собой уже не вероятность нулевого

- базовая вероятность для расчёта характеристик СМО;

h ( - p = n l — ^{m 8 h}    =1 V m

E gm

R^p

I         f ^P 0

I     m !

• -    вероятность полной занятости системы;

1 ^h

P w =   2 R i P Bi

R 0 i = 1

• -    вероятность ожидания обслуживания вновь прибывшей заявкой в физической очереди.

В этом случае относительная пропускная способность системы q = P_w , абсолютная пропускная способность, очевидно, A = Л _o q.

Моменты числа заявок, ожидающих обслуживания в физической очереди рассчитываются по той же схеме, что и для математической очереди, однако в соответствующие формулы подставляются вероятности с тильдой, полученные с учётом соответствующего условия нормировки. Подробный вывод формул для моментов длины очереди приводится в работе [5]. В результате имеем

• -    среднее число заявок, находящихся в физической очереди

P =

r Г m R m р

I               1

m J x i- m - E1 / EF

P |       ( R1 | m Jl

m <  i <  m + E_x

Rm

—— P , i >  m + E_x m !

В данной модели принята следующая система обозначений:

P o =—; P 1 =—;

и     и

X p = -;

и

л₀            „ Л

R o =— = P o ⁺ P 1 ⁺ p ; ^R 1 =—= P 1 ⁺ P ^.

и              и

В этом случае первый и второй моменты числа заявок, ожидающих обслуживания в физической очереди имеют вид

l =

—Ry ( PB1 - E1 Pm+E, ) ,  R1 * m m - R1 x

E 1 +¹ p p R = m

I 2 ^B 1 ,      ¹

> +

h

1 =2

i = 1

"'  [ Pb-- EPm+£ ], R* m m - R.             iJ

Ei ( ^e - + 1 ) p

-          m+£ - 1 ^

h

+2 £i i=2

R = ^m

Ri

' i - 1        ¹ BI ;

m

- второй начальный момент числа требований в физической очереди

h

R ( m + R

^{1 2} = 2 £ -1 P Bi ⁺1 m — R l m — ^Ri

i = 1

mE_t („ ,  2 R

----” Ei +-- m - R l m - R

⁺ 2 ^£ i - 1

⁺ 2 ^£i-1 I ^PBi

где

( E i - 1 ) E i

( 2 E - 1

l 6

^{+ £} i - 1

m +£ i ,

R. * m

R = m

+

^+£ h P m+£_h *

Приведём также варианты этих зависимостей для нескольких частных случаев, представляющих определённый практический интерес. Для комбинированной модели массового обслуживания, представленной в работе [4], имеем

Л

P o =

m R ₀ m !

1 +

l

R 1

m - R₁

E ₁

1 "I ^R I l m J

E , R = m

E 1

⁺I “ I ---- l m J m - p J

- 1

;

, R * m

+

при этом вероятности стационарных состояний

(E,

+ p I — + l m

T2=\-R1

—¹— Ir * 1 ¹ FLS ;

m - p J m + Ra

m - R_x m - R_t

^f £ ₊ ^{2 m} |p

E ¹ 1 E ^{1 +} m - R J P^{m +} E 1

E 2

+ p — + m

^

³ = У p

FLS   2 i i=m+E1

B 1

, R_x * m

> +

m - p

^P B 1 , ^R 1 = ^m

2 E + m +P m - p

FLS ,

— вероятность полной загрузки

накопителя, p — приведенная интенсивность

потока заявок, для которых не действуют огра-

ничения на длину очереди.

Для частной модели СМО с полным набором накопителей, предложенной в работе [6], вероятности стационарных состояний системы при расчёте физической очереди принимают вид

mmh g

Ro + Ro   rTR_ • m! m!    у =1 m ’

~   i - m R Rm ~ p =П—-°- p,  m +1 < i < m + h.

g = 1 m m !

и тогда моменты числа заявок, ожидающих обслуживания в физической очереди

P o =

m + h          i - m D mm

l ⁽ K ) = 2 ( - - m ) K П R g R 7 P K = '-2. i = m + 1          ^ = 1 m m !

Для модели Х. Такаджи [7] вероятности стационарных состояний системы для расчёта физической имеют вид:

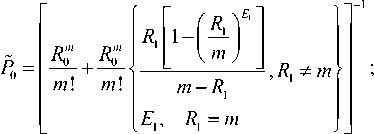
/ D у ^m mm

P =| -1 I  ^0-P,  m

V m ) m !

^{m -} Р 1

^Е ■ '

I 2   ’

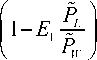
Р 1 = т

Р * m

7 2

Р 1 ⁽ m ⁺ Р 1 ) ( ^{m -} Р 1 ) ²

;

Р 1 ^Е 1 | р , ^m

-------I ^Е 1⁺------- m - р V m - р

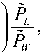
р * m .

Р = m

и моменты числа заявок, ожидающих обслуживания в физической очереди

l = ]

__-i n I PB1  Е1 Pm+Е Ь m - —,

Е + 1^

2   ^P b i ,   ^— i = ^m

— i    m + — i 5

PB m - — ^ m - —

Е 1 ( Е 1 + 1) (2 Е 1 + 1)

В этих формулах

P

P W = ]

( m - 1 ) ! ( m - р )

m m ^{- 1}

J m - 1)!

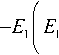
m- ¹ p „ m - — ) m ^{+ E1}

( E 1 + 1 )( 2 E , + 1 )

-           PB 1 ,

, — 1 * m

^— 1 = ^m

Точно такая же система формул будет, очевидно, действительной и для однокомпонентной модели СМО с очередью конечной длины (по классификации Дж. Кендалла - модель M/M/m/E). В этом случае в вышеуказанных формулах следует лишь положить — о = — 1 = Р 1 , откуда в соответствии с [2, 3] имеем

P 0 =

Rm  m m! m - р

P i =| ^р

V m

i - m

В этом случае первый и второй моменты числа заявок, ожидающих обслуживания в физической очереди

7- • V = Р ⁽ m + Р ⁾ P.

l            P FLS ;         (      V   ^FLS .

m - р          ( m - Р )

Для наиболее простой однокомпонентной модели с неограниченной очередью (модель M/M/m) в формулах (2) следует принять — ₀ = р и в

этом случае отсюда имеем

-        р = р ^{( m +} р )

m - р ’       ( ^{m -} р )

Время ожидания начала обслуживания заявкой в физической очереди. Алгоритм расчёта моментов времени ожидания обслуживания заявкой в физической очереди вполне идентичен алгоритму расчёта моментов времени ожидания заявки в обычной математической очереди, приведенному в работе [5]. В нем вместо обычных вероятностных характеристик лишь следует под-

/    X ^Е 1

1 -( Р I

V m )

^Е 1 P 0 ,   Р 1 = ^m

, Р * m

- вероятность ожидания заявкой обслуживания,

то есть вероятность того, что поступающее требование найдет все каналы занятыми

Р 2 + ^Е 1 р

1    Е,    0, m! m 1

m - 1

m _P

( m - 1)!

Р * m

Р 1 = m

- вероятность отказа, который заявка получает, если приходит в момент, когда заняты все m обслуживающих каналов и все Е 1 мест в очереди.

Наконец, для частной модели, впервые изученной в работе Дж. Коэна [1], имеем следующие вероятности стационарных состояний системы для расчёта параметров физической

очереди:

। о, m !

i >  m .

ставить соответствующие вероятности с тильдой, полученные с учётом нового условия нормировки (1). Кроме того, с учётом этого обстоятельства следует переопределить относительную пропускную способность системы q . В данном случае для универсальной модели СМО, представленной работе [5], имеем следующие конечные формулы для моментов времени ожидания заявки в физической очереди:

i = - У J W A t r

' — i [ P Bi - E i P m +,]   —

m - —

^ W = Л ^X

A

° i - Г Bi m

l

A'

' ² ( P Bi - ^Е^^р. . . . ) Г

h

\ — i ] i = 1

р ( ^{m - —}i ) ²

p m

3pm2

1 + 5 ⁱ — ¹ ( m - — ) + m

Eg

i - 1 ( — i

П УI  [£i(fi+1)(fi+2)

g = 0 V ^—i )

—

⁸ 1 - 1 ( ^ i I + ^{1 ) P}Bi    E i ⁽ E i + ^{1 )} P m+:      ,

+--- m p m p ( m - R ) , ^M m \ .

^- E i - i (- 1 + O^ i - + ²) ] , R i = ^m

Для комбинированной модели массового обслуживания, приведенной в работе [4], при этом имеем tw = ^ A

R ₁

n I PB1  E1 Pm+E J + m - R x          17

₊ P>   \_E .

+   PFLS I E1 + m ^ m - p

l

A ^;

- дисперсия времени ожидания заявки в физической очереди

°"w

(E1 +1)(E1 + 2) p -12,

_     3 я A

= " ^{( E + 1 )(} E + ^{5 )} , p = m

[

.

Наконец, для модели Дж. Коэна [1]:

• -    \ D -     IP -    ^2pPILs>

• t =         P =   • tw =

^w Am - p FLS A’      A P ( ^{m -} P )

Для наиболее простой однокомпонентной модели с неограниченной очередью (модель M/M/m) при условии R o = p отсюда, очевидно,

2¹ tw    ~

A [ p ( m ^- R 1 ) _

2 - R ^ ( P b 1 - E 1 P m + E ) - m - R ^{x            17}

- E 1 ( E 1 + 1 ) P m + E ] ,

R_x * m

x

E 1²

—

3m p

^{1 P} B 1^,

^R 1 = ^m

p ( ^{m -} p )

2 ^ PFLS IE1 +      ^ + E1 ( E1 + 1) Pm+E m ^ m - p)             1

Для частной модели СМО с полным набором нако п ителей [6], имеем

7   —     1   m+h tW'=3; tw=:^^(i-m)(i-m+1)Pi■

A         A^{m p} i = m + 1

Для модели Х. Такаджи [7]:

t w

2 ¹ t w

1     R 1

Am - R,

( ^PB 1   ^E 1 ^Pm + E ) = p

1 _A

R 1

A ]_ ^ ( m ^{- R} 1 ) [ ² m ^{- R} 1

( P b 1 - E 1 P m + E , ) -

- E 1 ( E 1 + 1 ) P m + E 1 ] , R 1 * m'

—---Pb i, R

B 1    1

3 m p

= m

₊ E 1 ( E 1 + ¹ ) P A p m     ^{m + E1 .}

Эти же формулы будут справедливыми

и

для классической модели M/M/m/E, если в них положить R 0 = ^R ₁ = ^p ₁ , в этом случае имеем

l

‘^w = A H

P 1 ( ^PW  ^E 1 ^PL )

A ( m ^- P 1 )   ’

E , + 1

—¹-- , p = m

2 Я      ¹

p * m

;

следует

~ _ p _lCT ² =_____²_____.

t w                    л;      w     2          \2

Я ( m - p ) Я      p ( m - p )

Следует отметить, что результаты, полученные по этому алгоритму, полностью совпадают с результатами имитационного моделирования СМО вышеуказанных типов в системе имитационного моделирования GPSS World.