Физически-нелинейный расчет железобетонных балок-стенок с трещинами методом конечных элементов

В рамках физически-нелинейного расчета процесс изменения напряженно-деформированного

где

состояния конструкции исследуется путем малых приращений нагрузки. По мере роста нагрузки железобетон последовательно проходит ряд стадий напряженно-деформированного состояния:

• •    упругую без трещин;

• •    упругопластическую без трещин, где учитывается нелинейность деформаций бетона;

• •    стадию с трещинами до начала пластического деформирования арматуры;

k — ^T b ,min / Rb\ ; c — 1,48 - 0,055 R _b .

• •    стадию с трещинами, где учитывается развитие пластических деформаций арматуры.

Переход в иную стадию деформирования ус-

танавливается анализом системы очевидных ограничений. Напряжения, при которых в растянутом бетоне образуются трещины, определяются с учетом влияния факторов плоского напряжен-

ного состояния

^T b , crc

( 1 - c ) k 1 - ck

R bt ,

На стадии без трещин бетон рассматривается как физически-нелинейное ортотропное тело, оси ортотропии которого n и t совпадают с направлениями главных напряжений o b_n = o b,_max и T bt = CT b,_min . Связь между напряжениями и деформациями в координатах х , у записывается в виде

Ы — [ C ( T b ) ] Н b . (4)

Основными физическими характеристиками ортотропной модели являются секущие модули деформаций бетона E bn и E' bt и коэффициент поперечных деформаций v . Секущие модули деформаций бетона вычисляются в зависимости от вида напряженного состояния (сжатие-сжатие, сжатие-растяжение или растяжение-растяжение) и величины главных напряжений,

чем обеспечивается зависимость [ С ] b = [ C( o b ) ]. Коэффициент поперечных деформаций бетона определяется по методике [1] и также зависит от вида напряженного состояния и уровня напряжений в бетоне.

Для бетона до образования трещин справедливы зависимости sin 2 a cos 2 а

--+---------------;

E bn         E bt

v ( 1 + m )

mEbn + Ebt ’ f 1       1 | sin 2 a

I - E s J 2 ; .

cos ² a sin ² a + ;

E bn         E bt

1       1       2 v ( 1 + m )

++     ;

Ebn   Ebt   mEbn + Ebt m — 7b.max /7b.min где a - угол направления главных осей n и t по отношению к осям х и у.

После образования трещин элементы матрицы жесткости железобетона вычисляются по формулам (1.57) [2]. В случае только ортогонального армирования эти формулы существенно упрощаются и принимают вид:

~

C rc .11

A x , t       + cos ² a _;

E Sx Ц x + E Sp Ц p      E b

~

C rc .12 — 0;

~ C rc .13

A x , t ctg a       sin 2 a _

E Sx Ц х + E Sp ц p    2 E _b ’

~          ^A y , t

Crc .22 — —

Esу Цу sin 2 a

E b ;

f (6)

~ C rc .23

~

C rc .33 —

A y , t tg a   sin 2 a

E Sу Ц у     2 E b ’

Ax,tctg 2a      Ay,ttg 2a 1 f 2

--111 —1

ESx Цx + Esp цp    ESу цу    Eb V vn

В формулах (6) средними модулями деформаций арматуры E C, i=x, у учитывается влияние растянутого бетона на участке между трещинами на деформации арматуры. При частично нарушенном сцеплении E ' _Si > E _Si , при полностью нарушенном E 'i , = E _Si . Если 7 _Si >  о _Si,el , то при вычислении средних модулей деформаций арматуры учитываются пластические деформации стержней на участке между трещинами.

На первой итерации каждого этапа нагружения секущий модуль деформаций бетона принимается равным модулю упругости. После выполнения расчета в конечном элементе (КЭ) получают некоторые напряжения о ¹ ! и деформации £\ (где верхний индекс означает номер этапа нагружения, а нижний – номер итерации). Далее

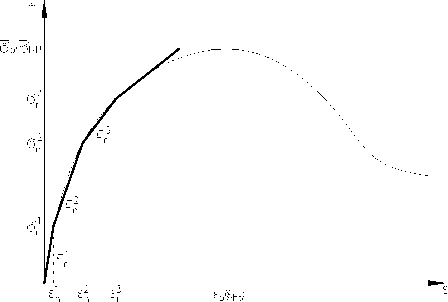
Рис. 1. Характер зависимости между напряжениями и деформациями

в соответствии с полученными напряжениями и деформациями корректируется секущий модуль деформаций и назначается его новое значение E 1 ¹ . На следующих итерациях расчет повторяется при постоянной нагрузке. На каждом этапе нагружения расчет прекращают после заданного числа итераций или при удовлетворении условия сходимости. По полученным напряжениям ст П и деформациям f n в КЭ корректируется секущий модуль E n ¹ . Характер зависимости между напряжениями и деформациями приведен на рисунке 1.

Если в процессе расчета в некотором КЭ напряжения 7 mn или деформации £ mn в бетоне превысили их предельные значения, то на последующих итерациях в этому элементе задают новое значение секущего модуля бетона E mn , равное 0,5 E m n - 1 . Физически смысл такой операции состоит в том, что в процессе разрушения элемента его постепенно выключают из работы [3, 4].

Для расчета по предложенной методике была выбраны балки-стенки из опытов М.П. Нильсена (Nilsen M.P.) [5]. Балки-стенки высотой h = 100 см, толщиной t = 8 см и пролетами l = 100 см (балка-стенка №101) и l = 200 см (балка-стенка №103) были испытаны на кратковременную нагрузку. Армирование балок-стенок осуществлялось по всему полю однородной сеткой из проволоки диаметром 6 мм и шагом 100 мм ( Ц x — Ц у — 0,0035). Физикомеханические свойства арматуры приведены в таблице 1. Схемы армирования балок-стенок приведены на рис. 2.

Таблица 1

Физико-механические свойства арматуры

	E s	7 s , el	7 0,2	7 u	f SU
	МПа	МПа	МПа	МПа	–
Арматура диаметром 6 мм	210000	410	510	680	0,025

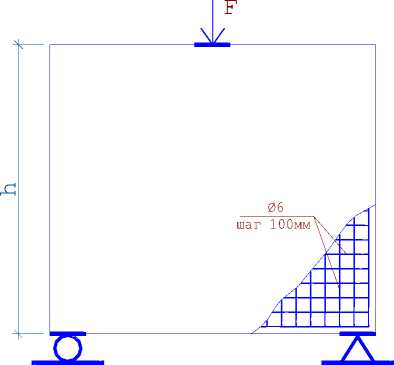
Рис. 2. Конструкция балки-стенки

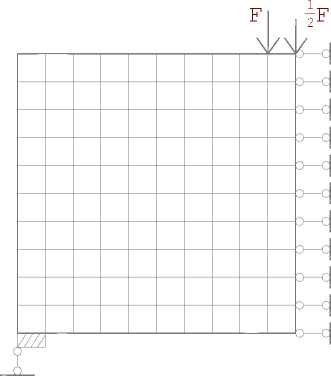
Рис. 3. Расчетная схема балок-стенок

Если в процессе расчета в некотором КЭ напряжения σ mn или деформации ε mn в бетоне превысили их предельные значения, то на последующих итерациях этому элементу задают новое значение секущего модуля бетона E mn , равное 0,5 E m n - 1 . Физически смысл такой операции состоит в том, что в процессе разрушения элемента его постепенно выключают из работы [3, 4].

Для расчета по предложенной методике была выбраны балки-стенки из опытов М. П. Нильсена (M. P. Nilsen) [5]. Балки-стенки высотой h = 100 см, толщиной t = 8 см и пролетами l = 100 см (балка-стенка №101) и l = 200 см (балка-стенка № 103) были испытаны на кратковременную нагрузку. Армирование балок-стенок осуществлялось по всему полю однородной сеткой из проволоки диаметром 6 мм и шагом 100 мм ( µ x = µ y = 0,0035 ). Физико-механические свойства арматуры приведены в таблице 1. Схемы армирования балок-стенок приведены на рисунке 2.

Физико-механические свойства бетона балок-стенок приведены в таблице 2.

При расчете симметричные части балок-стенок № 101 и № 103 были разбиты на 51 и 100 прямоугольных КЭ, соединенных 68 и 123 узлами соответственно. Расчетные схемы балок стенок представлены на рисунке 3.

На рисунке 4 представлены графики прогибов балок-стенок. Как в опыте, так и в расчете балки-стенки загружались до разрушения. В балке-стенке № 101 опытная нагрузка трещино-образования составила 145 кН, расчетная 120 кН. В балке-стенке № 103 опытная нагрузка трещинообразования составила 78 кН, расчетная – 90 кН.

Как в эксперименте, так и в расчете образование первых трещин не привело к существенному нарастанию прогибов. Как следует из графиков (см. рис. 4) и анализа напряженного состояния конечных элементов, нелинейность деформирования резко возросла с началом текучести продольной растянутой арматуры, сокращением высоты сжатой зоны и сопровождалась нарастающим раскрытием нормальных и наклонных трещин. Как в опыте, так и в расчете разрушение балок-стенок явилось следствием текучести продольной растянутой арматуры и исчерпания прочности сжатого бетона. Схемы образования и развития трещин в балках-стенках представлены на рисунках 5 и 6.

Сопоставление теоретических и опытных данных позволяет сделать вывод, что представленная модель и методика расчета с достаточной степенью точности описывают нелинейное поведение железобетона с трещинами.

Таблица 2

Физико-механические свойства бетона

Балка-стенка	Цилиндрическая прочность	Кубиковая прочность R (20х20см)	Призменная прочность R b	Прочность при осевом растяжении R bt	Модуль упругих деформаций E b
	МПа	МПа	МПа	МПа	МПа
№101	41	49,4	35,6	2,54	36000
№103	37	44,6	32,4	2,41	34500

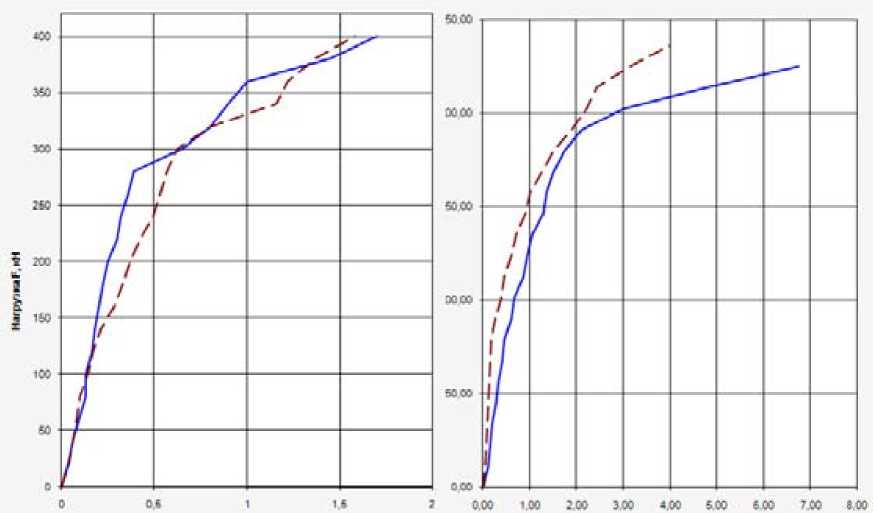
Рис. 4. График прогибов балки-стенки №101 (слева) и балки-стенки №103 (справа).

Обозначено:         опыт;          расчет.

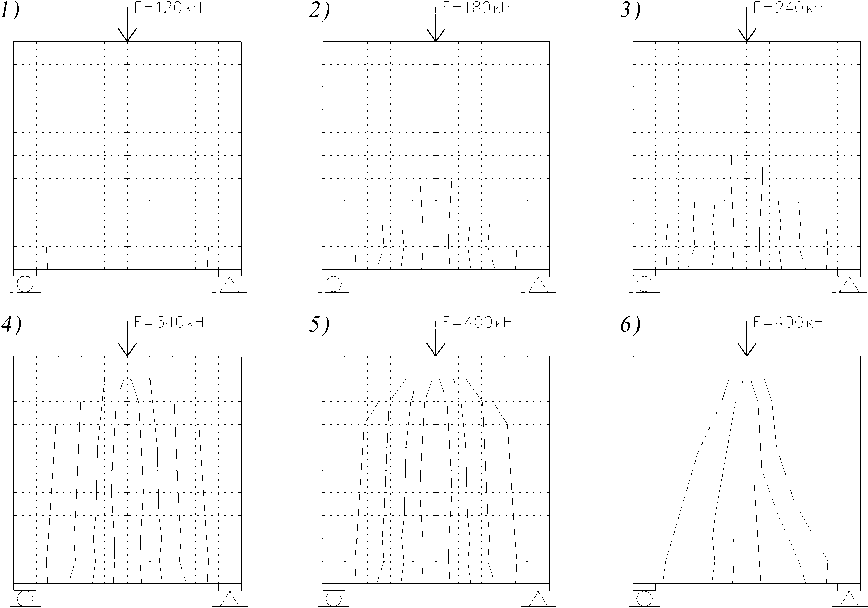
Рис. 5. Схемы развития трещин в балке-стенке №101 1-5 – расчет; 6 – опыт

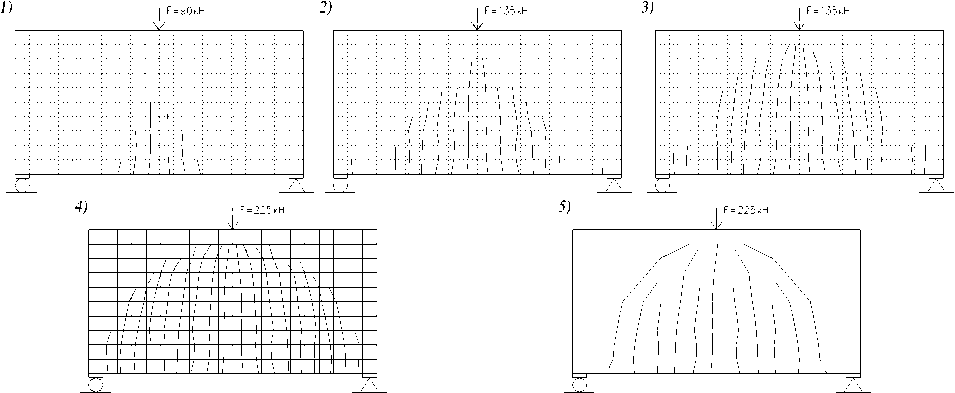
Рис. 6. Схемы развития трещин в балке-стенке № 103 1-4 – расчет; 5 – опыт