Физические основы электрографии

Среди методов исследования электрической активности органов и тканей наибольшее распространение получила электрография. Данный метод заключается в регистрации временных изменений электрических потенциалов полей, создаваемых органами или тканями на поверхности тела. В основу электрографии положен метод моделирования органа в виде эквивалентного электрического генератора. Причем потенциалы поля, создаваемые таким эквивалентным генератором, должны быть близки значениям потенциалов реального органа или ткани, регистрируемым на поверхности тела (принцип эквивалентного генератора) [1].

Для того чтобы понять, какой физический объект выбрать в качестве эквивалентного генератора, рассмотрим клетку, окруженную электрически заряженной мембраной. В покое внутренняя поверхность мембраны заряжена отрицательно относительно наружной поверхности (рис. 1). Возбужденные участки мембраны поляризованы противоположно: внутри положительно, снаружи отрицательно. Таким образом, возбужденные и невозбужденные участки клеточных мембран можно рассматривать как совокупность электрических диполей.

Важно отметить, что среда, окружающая клетки, представляет собой проводник. В такой среде диполь может сохраняться только в случае, если он является источником тока. Действительно, на клеточной мембране происходит разделение электрических зарядов за счет неодинаковой проницаемости для разных видов ионов, а также работы встроенных в нее белков (так называемых ионных насосов), использующих энергию, выделяемую при гидролизе молекулы АТФ. Поэтому с физической точки зрения данная система является источником тока.

внеклеточная среда

аб

клеточная мембрана

внутриклеточная среда

Рис. 1. Схема клеточной мембраны с невозбужденными (а) и возбужденными (б) участками (стрелками показано направление электрических токов)

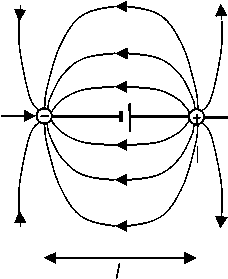
Система, образованная положительным и отрицательным полюсами источника тока, помещенными в однородную проводящую среду на некотором расстоянии друг от друга, получила название токовый диполь (рис. 2). Основная характеристика токового диполя - это его дипольный момент

D = 1 1 , (1) где I - полный ток, протекающий от положительного полюса к отрицательному, l - расстояние между полюсами (плечо диполя).

D

Рис. 2. Полюсы источника тока, помещенные в однородную проводящую среду, как токовый диполь

В соответствии с данным определением дипольный момент клетки - вектор, направленный от возбужденного участка наружной поверхности мембраны к невозбужденному. Тогда дипольный момент органа или ткани представляет собой векторную сумму дипольных моментов наружных мембран поверхностного слоя их электрически активных клеток [2]. По- лучающийся при этом вектор называется результирующим (интегральным) дипольным моментом органа.

Распределение электрического потенциала поля токового диполя. Выбрав в качестве модели электрически активного органа токовый диполь, можно перейти к расчету распределения потенциалов создаваемого им поля. Вначале найдем потенциал поля уединенного положительного полюса источника тока (монополя) в однородной проводящей среде на произвольном расстоянии r от него (рис. 3).

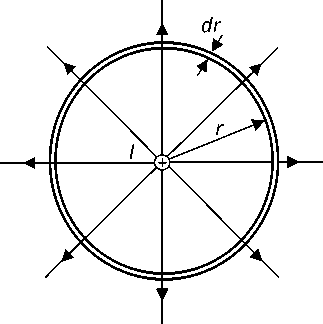
Рис. 3. Уединенный положительный полюс источника тока в однородной проводящей среде

Рассмотрим сферический слой радиуса r и толщиной dr , в центре которого расположен

монополь.

Пусть I - сила тока, протекающего через слой поверхностью S . При этом ( - d ф )

– падение записать:

электрического потенциала на этом слое.

В соответствии с законом Ома можно

• -    d ф = I d R ,

dr где d R = р — - сопротивление выделенного слоя,

S = 4 п r - площадь его поверхности,

р - удельное сопротивление среды.

Тогда

dr

• -    d ф = I р-----

• 4 п r 2

.

Проинтегрируем обе части выражения (3):

0             га

- J dф = IРJ

ф

r

dr

,

• 4    п r

и тогда для потенциала поля монополя получаем:

I Р ф =

4 п r

.

Найдем выражение для потенциала ф поля, создаваемого токовым диполем в точке A, находящейся на большом расстоянии r от него (рис. 4).

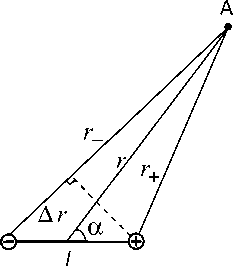
Рис. 4. К расчету электрического потенциала поля, создаваемого токовым диполем в точке А

Потенциал ф в точке A равен алгебраической сумме потенциалов положительного и от- рицательного полюсов в этой точке:

ф = ф₊+ф —

IT ^f "1 - "1' 4 п ( r ₊ г - )

I p ⁽ r _ - r + )

4 п r ₊ r -

A r = r _ - r ₊ « l cos a , для потенциала

С учетом того, что r >> l, r+ = r- ~ r, r+ r_ ~ r имеем:

_ I p l cos a _ p D cos a

.

^{4 п} r ²      4 п r ²

Из полученной формулы следует, что потенциал ф поля токового диполя в точке A за- висит от величины электрического момента диполя и от угла между осью диполя и направлением на точку A.

Используя формулу (6), найдем выражение для разности потенциалов электрического поля диполя в точках A и B. Для удобства предположим, что эти точки равноудалены от диполя г а = г в = r >>  l (рис. 5):

.                p D cos a   p D cos a_R    p D

^A Ф AB = Ф A ^- Ф B =------ 5---5— =---- у ^{( cos a} A ^{- cos a} B ) ,⁽⁷⁾

4 п г ²       4 п r ²     4 п r ²

п в где a a = a + — - 2 - угол между вектором D и направлением от диполя до точки A, п В_ a в = a + — + 2 - угол между вектором D и направлением от диполя до точки B.

Тогда p D a,+a a,-aR p D        2 a + п

Аф =-^— -( - 2 ) sin-^--- B sin-^--- B = -^— -( - 2 ) sin-----sin - =

AB 4 п r2 V ’        2            2       4 п r2 V ’       2

p D . f   п) . В p D cos a . В sin a+   sin— =

2 п r2 I    2) 2 2 п r22

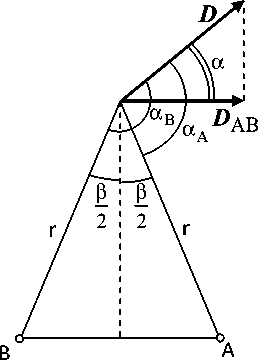
Рис. 5. К расчету разности потенциалов поля токового диполя в точках A и B, равноудаленных от диполя

Как видно из формулы (8), данная разность потенциалов Δϕ _AB пропорциональна проекции D_AB момента токового диполя на прямую, соединяющую точки A и B.

Результирующий дипольный момент сердца. После того, как мы нашли соотношение, связывающее проекцию дипольного момента источника с распределением потенциалов создаваемого им поля, необходимо указать способ, в соответствии с которым по наблюдаемой разности потенциалов можно определить пространственную ориентацию вектора дипольного момента эквивалентного генератора органа в данный момент времени. Применительно к сердцу данную задачу решил нидерландский физиолог В. Эйнтховен (1913). Он предложил измерять электрические потенциалы сердца в точках, представляющих вершины равностороннего треугольника (так называемый треугольник Эйнтховена), в центре которого находится результирующий дипольный момент сердца [3]. Эквипотенциальные линии поля, генерируемые сердцем, проходящие через вершины этого треугольника, выходят на правую руку, левую руку и левую ногу (пунктирные линии на рис. 6).

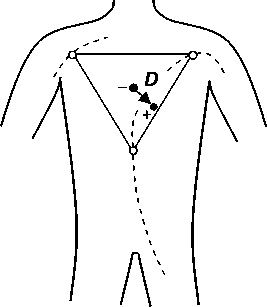
Рис. 6. Схема треугольника Эйнтховена

Это позволяет стандартизовать измерения потенциалов сердца и получить информацию о величине и направлении дипольного момента сердца во фронтальной плоскости тела. В электрокардиографии I стандартным отведением называется соединение милливольтметра с левой и правой руками, II отведение – правой руки и левой ноги, III отведение – левой руки и левой ноги. Тогда, следуя соотношению (8), можно показать, что разность потенциалов между вершинами треугольника Эйнтховена пропорциональна проекции вектора дипольного момента на соответствующие стороны треугольника (рис. 7):

Δϕ _AB ~ D_AB = D cos α _AB ,

Δϕ _AC ~ D_AC = D cos α _AC ,

Δϕ _BC ~ D_BC = D cos α _BC .                         (9)

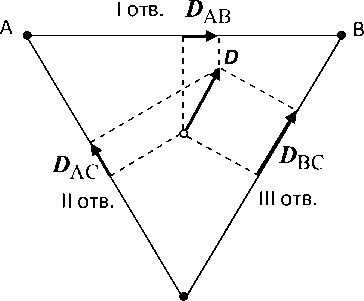
C

Рис. 7. Построение вектора дипольного момента D в треугольнике Эйнтховена

Следовательно, измерив с помощью милливольтметра разность потенциалов между вершинами равностороннего треугольника в соответствующих отведениях, можно определить величину и направление вектора дипольного момента D во фронтальной плоскости.

В процессе распространения электрического возбуждения в сердечной мышце непрерывно изменяется направление результирующего вектора, его величина. Поэтому разность потенциалов, измеренная милливольтметром в соответствующих отведениях, будет меняться со временем.

График зависимости разности потенциалов Δ ϕ в данном отведении от времени t называется линейной электрокардиограммой (рис. 8). Каждый такой график отражает величину проекции результирующего вектора на направление, соответствующее данному отведению.

Δϕ

Рис. 8. Схема типичной линейной электрокардиограммы

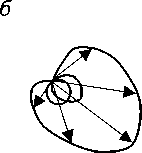
Чтобы получить информацию об изменении вектора дипольного момента на плоскости, необходимо сложить результаты измерений величины проекции дипольного момента в двух взаимно перпендикулярных направлениях в этой плоскости, то есть, получить фигуру Лиссажу (рис. 9а) [1]. Данная фигура является векторэлектрокардиограммой. Векторэлектрокар-диограмма представляет собой линию, описываемую концом вектора результирующего дипольного момента сердца за цикл электрической активности в проекции на заданную плоскость (рис. 9б). Например, складывая отведения, расположенные вдоль горизонтального и вертикального направлений, получаем проекцию дипольного момента сердца во фронталь- ной плоскости. Чтобы проследить за поведением результирующего вектора в пространстве, необходимо построить векторэлектрокардиограмму в саггитальной и горизонтальной плоскостях, выбрав соответствующие направления отведений.

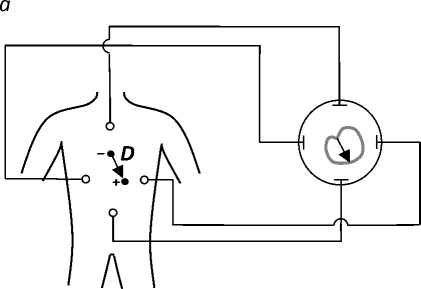
Рис. 9. Схема получения векторэлектрокардиограммы с помощью электронно-лучевого осциллограф (а).

Проекция векторэлектрокардиограммы на фронтальную плоскость (б) за один сердечный цикл

Заключение. В предлагаемой работе рассмотрены физические вопросы электрографии органов и тканей. Представлены основные этапы изложения данной темы: от выбора модели электрической активности биообъектов и простейших математических соотношений, связывающих источник и создаваемое им поле, до способов регистрации электрических потенциалов, генерируемых органами и тканями на поверхности тела. Настоящая работа может быть полезна при изучении курсов физики, нормальной физиологии и кардиологии в высших медицинских учебных заведениях.

Автор выражает глубокую благодарность доценту кафедры медицинской и биологической физики Самарского государственного медуниверситета А.И. Сироте за плодотворное обсуждение затронутых в статье задач и оказанную помощь в работе, а также доценту кафедры физики Поволжского государственного университета телекоммуникаций и информатики М.В. Головкиной за анализ статьи, что способствовало ее улучшению.