Физические основы электропроводности сильно ионизированного воздуха

При решении прикладных задач, связанных с зоной ионизации мощных импульсных источников ионизирующего излучения, возникает необходимость исследования шунтирующих свойств ионизированного воздуха. Например, в ходе радиационных испытаний электрические цепи электронных устройств могут значительно шунтироваться ионизированным воздухом, что приводит к значительным искажениям результатов этих испытаний. Шунтирующие свойства ионизированного воздуха представляют интерес также при различных электрических измерениях в зоне ионизации электронных ускорителей, которые широко используются в процессе разработки высоких технологий.

Электропроводность сильно ионизированного воздуха

Воздействие на воздух любого ионизирующего излучения сводится к образованию в нем лавин вторичных электронов. Рожденные на последних стадиях электронных лавин вторичные электроны, имеющие энергию меньше потенциала ионизации, определяют электрофизические свойства ионизированного воздуха. Проводимость ионизированного воздуха в этом случае определяется как процессами ионизации, так и целым комплексом различных деионизационных процессов (электрон-ионная рекомбинация, ион-ионная рекомбинация, прилипание электронов к нейтральным молекулам кислорода). В статье представлены результаты исследования проводимости воздуха в условиях его облучения нестационарной радиацией (энергия релятивистских электронов порядка 1 МэВ).

Проводимость ионизированного газа может быть записана в виде о = е (ц+ион^+ + и ион^- + µэлn),                                    (1)

где µ ⁺ _ион , µ ^– _ион , µ _эл – подвижность положительных, отрицательных ионов и электронов соответственно; N + , N _- , n — их концентрации.

Концентрации электронов и ионов найдем из уравнения баланса между скоростями ионообразования и деионизационных процессов:

d n

— = q - aNn - yn, dt          + dN

—- = q - aN n - PN N , d t              ⁺         ' "

dN

— = yn - PN+ N-, dt где q – число электрон-ионных пар, образующихся в 1 см3 воздуха в течение 1 с под влиянием излучения; γ – частота прилипания электронов к молекулам воздуха (преимущественно к кислороду), величина, обратная среднему времени жизни электрон-ионных пар; α и β – коэффициенты рекомбинации положительных ионов с электронами и отрицательными ионами соответственно.

Наиболее часто радиационные исследования проводят в зоне ионизации электронных ускорителей, где ионизация воздуха осуществляется электронным пучком.

Скорость ионообразования q можно найти, зная потери энергии релятивистских электронов на единице ∂E пути [1], плотность тока пучка электронов j и энергию, необходимую для одной электрон-ионной ∂x пары Wе [2].

В области энергий от 1 до 10 МэВ (энергия типична для электронных ускорителей, используемых для радиационных исследований) ионизационные потери остаются неизменными и могут быть приняты равными 1,6·10 ⁶ эВ·см ² ·г ^–1 [1; 2].

Примем плотность тока пучка ускорителя j = 10 мА/см2, а энергию Wе = 34 эВ. Получим для воздуха нормальной плотности q = 3,5·1018 с–1·см–3

.

Электрофизические свойства ионизированного газа определяются в основном поведением электронной компоненты, которая на четыре порядка более подвижна, чем ионная.

Процесс прилипания электронов к нейтральным молекулам воздуха при давлениях, близких к нормальному, протекает значительно быстрее электронной рекомбинации. Действительно, скорость прилипания определяется частотой прилипания γ, с ^–1 , согласно экспериментальным исследованиям [3] при нормальном давлении равна 1,1·10 ⁸ с ^–1 и зависит от давления согласно [4; 5]:

γ = 1,1·108Ф2 + 2,6·106Ф, где Ф = Р/Р0, здесь Р0 – нормальное давление.

Состояние ионной компоненты будет определяться диссоциативной электрон-ионной рекомбинацией и трехчастичной рекомбинацией, когда избыточная энергия отдается третьей нейтральной частице, тогда коэффициент рекомбинации положительных ионов с электронами α может быть принят согласно [5]: α = (2,9 + 1,7Ф)·10 ^–7 см ³ ·с ^–1 .

Рекомбинация положительных ионов с отрицательными ионами может происходить в двойных и тройных соударениях, и коэффициент ион-ионной рекомбинации β ≈ (5·10 ^–2 + 2,5Ф)·10 ^–6 см ³ ·с ^–1 [6; 5].

В работе [7] приведена подвижность электронов в воздухе в зависимости от давления, полученная экспериментально СВЧ-методами при измерении частоты соударения электронов с нейтральной компонентой и составляющая µ э = 2,6·10 ⁹ Р ^–1,2 ед. СГСЭ, где Р – давление воздуха, Торр .

Для нормального давления (760 Торр) µ э = 9,1·10 ⁵ ед. СГСЭ.

Для стационарного случая концентрация электронов при плотности тока пучка j ≈ 10 мА·см ^–2 cоставляет n = 3,3·10 ¹⁰ см ^–3 и проводимость воздуха определяется электронной компонентой σ = 1,4·10 ⁷ ед. СГСЭ (с ^–1 ).

При решении ряда прикладных задач возникает необходимость расчета нестационарной проводимости воздуха (например, при исследовании переходных характеристик различных измерительных преобразователей, работающих в зоне ионизации радиационных установок). Нестационарная проводимость рассчитывается по формуле (1) с использованием системы (2).

Зададим скорость ионообразования с помощью функции Хевисайда в виде прямоугольного импульса длительностью 10 ^–6 с и временем задерживания 10 ^–7 с. Положим, что амплитуда импульса q 0 = 3,5·10 ¹⁸ см ^–3 с ^–1 .

Для положительных ионов подвижность µ ⁺ ион примем равной 4,2·10 ² ед. СГСЭ, аналогично для отрицательных ионов µ ^– ион = 5,4·10 ² ед. СГСЭ [8].

На рис. 1–3 показаны результаты численного интегрирования системы (2).

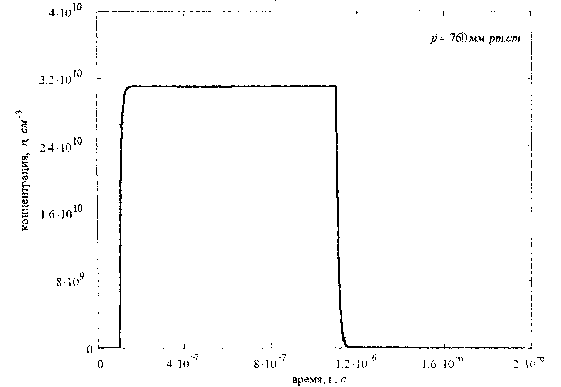
Рис. 1. Зависимость концентрации электронов от времени

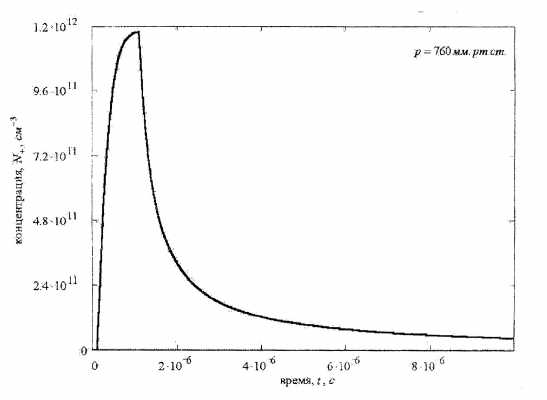
Рис. 2. Зависимость концентрации положительных ионов от времени

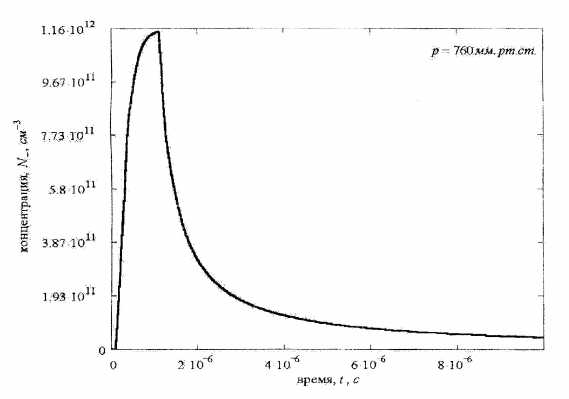
Рис. 3. Зависимость концентрации отрицательных ионов от времени

На рис. 4 показаны результаты численных расчетов нестационарной проводимости ионизированного воздуха с использованием формул (1) и (2).

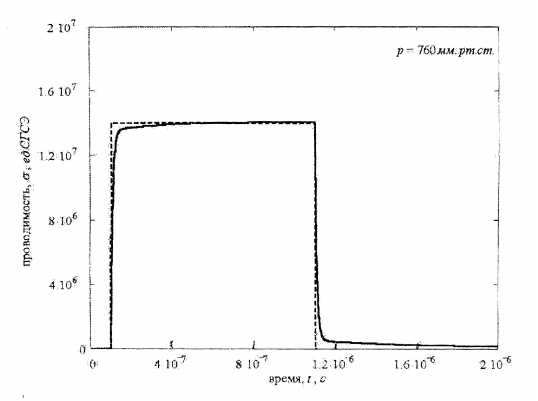
Рис. 4. Зависимость проводимости от времени при плотности тока пучка ускорителя электронов j = 10 мА·см ^–2

Из рис. 4 видно, что проводимость определяется поведением электронной компоненты и при этом практически повторяет форму пучка первичных электронов, таким образом, появляется возможность создания на этой основе методов измерения ионизационного эффекта.

Экспозиционная доза определена Рентгеном для атмосферного воздуха как стандартной среды, поэтому методы измерения проводимости могли бы стать основой импульсной дозиметрии высоких интенсивностей. Необходимо также отметить, что эти методы могли бы решить проблему зависимости чувствительности метода дозиметрии от энергии излучения ("хода с жесткостью"), что характерно для большинства методов, где в качестве первичного преобразователя используется среда, существенно отличающаяся от воздуха по атомному номеру. Эта проблема особенно остро стоит в дозиметрии однократных импульсов тормозного излучения, получаемых на сильноточных электронных ускорителях, где спектр излучения непостоянен от импульса к импульсу.

Преобладание электронной компоненты в проводимости воздуха позволяет при оценке ионизационного эффекта использовать лишь первое уравнение системы (2) и для квазистационарного случая (характерное время изменения потока радиации много больше 10–8 с) полагать q = γne.

Если принять частоту прилипания γ известной [5], то скорость ионообразования однозначно определяется концентрацией электронов n e , которая может быть определена экспериментально, например, одним из СВЧ-методов диагностики плазмы в пределах 10 ⁶ –10 ¹² см ^–3 [8].

Вывод

Скорость ионообразования в воздухе известным образом [1; 2] связана с мощностью экспозиционной дозы, что позволяет получить высокоскоростные методы абсолютных измерений мощности экспозиционной дозы.