Физические принципы диагностики в технологиях плазменного напыления

методов диагностики скорости, является уравнение непрерывности, описывающее движение потока ньютоновской жидкости (псевдогаза частиц), чувствительной к ударным вол-∂n       r нам: — + div(пи) = 0, где n=N(t)/V- концентра-∂t ция частиц в измерительном объеме V.

Введем обозначения: ц ( t ) = - ( д п /д t ) • V интенсивность потока частиц, пересекающих поперечное сечение измерительного объема V (число частиц в единицу времени); р _пог ( t ) = ( д п /д x ) • S = ( д п /д x ) • V/кl - погонная плотность частиц, приведенная к толщине измерительного объема A l , число частиц на единицу длины. Запишем уравнение непрерывности в одномерном виде: ц ( t )= р_поги . Отсюда определим скорость потока:

U = Ц / р пог              (1)

Интегральная скоростная характеристика (1) выражает скорость ансамбля или группы из N частиц, находящихся в определенный момент времени в измерительном объеме. Это позволяет перейти к модели многоскоростного твердофазного континуума. Континууму с номером i соответствует плотность p i , скорость Ui , ( i =1,2,..., K) и другие параметры.

Методика диагностики скоростных характеристик двухфазного потока заключается в последовательном выделении оптическими средствами теплового излучения одинаковых порций частиц потока, описываемых как континуумы, измерении времени пролета каждым континуумом известного базового расстояния, задаваемого несколькими фотоприемниками. В качестве оптического преобразователя, в общем случае должна применяться линейная многоэлементная матрица из M фотодиодов. Интенсивность потока частиц определяют по интенсивности светового излучения, а плотность потока частиц - по разности интенсивностей входящего и выходящего потока частиц в сечениях, задающих базовое расстояние пролета L (рис. 1).

d

f ( N j. ⁽ t »)

L v J

L

^A t кв

d (( N j. ( t )})

^A t кв

.

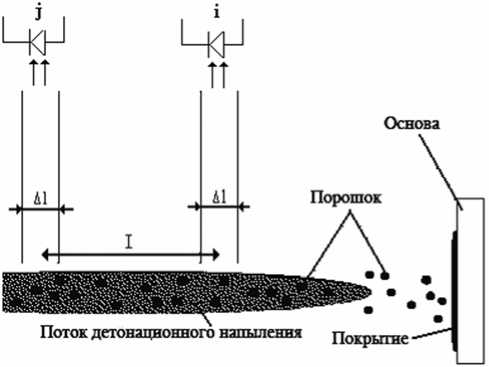
Рис. 1. Схема диагностики распределения скорости частиц конденсированной фазы

Число частиц, вошедших в j -ое сечение к моменту времени t , есть сумма числа частиц N j ( t ), входящих в сечение j за время dt , по рассматриваемому временному отрезку, то же справедливо и для числа частиц N i ( t ), вышедших за время t через сечение i.

t

^N „,( t ) = —    J ^J , ( T ) d T

K0 ^b 0V ) 0

z к1

NBbI xi (t) =---------f J(t ) dT, вых i

K0^0(T ) 0

где J j ( t ) и J i ( t ) сигналы фототока, снимаемые с j -го и i -го фотодиодов соответственно. На основе (3), (4) и (5) получим:

в потоке плазмы

( ^( t )) =

Количество частиц в i -ом сечении в некоторый момент времени t может быть найдено как произведение погонной плотности р пог на этом участке на ширину сечения A l :

N ( t ) = p i ( t ) A l .

a t кВ K 0^0(Т)

t

JAJ ji (t ) dT

Перепишем выражение (1) с учетом (3) и (6):

r

и =

t

J ^{A J}ji ⁽ T ) d T 0

Введем понятие средней погонной плотности частиц, как отношение разности числа частиц N_BX j ( t ), вошедших через j -ое сечение и числа частиц N_выхi ( t ) вышедших через i -ое, к расстоянию L между ними:

^A t .в ^K.-'T ) f jt )}У

L

v J

(Р (t)) =

N вых j ( t ) - N _вх i ( t ) = (,)} LL

Допустим, что изменением погонной плотности р пог между сечениями i и j можно пренебречь (меняется незначительно на выбранном интервале), тогда:

Запишем уравнение непрерывности для одномерного случая:

ji-пог V ) l

^N,⁽ t ) , N i ( t ) A l      A l

dk Р пог ⁽ t ))      d (д ⁽ t ))

--------=-- dt            dx .            (3)

Окончательно, для скоростей потока в сечениях i и j , выражая N ( t ) из (4) и проводя некоторые упрощения, получим следующие соотношения:

Из (3) изменение средней интенсивности ^d<Д ⁽ t )) в сечении L за период квантования сигнала A t_Ke будет равно (без учета знака):

Ц =

^d( ^ ( t )) = ^d ^Р пог ⁽ t ))

L

A t кв ,

t f AJji (t)dT

A l 0__________

A t _К в      J, ( t )

а с учетом (2), получим:

u =

t jAJji (t)dT a l i___________

A t _К в      J j ( t )

Максимальная прочность сцепления порошка с основой при напылении определяется степенью прогрева частиц порошка до температуры плавления без перехода основной массы частиц в жидкую фазу. Нагрев частиц порошка является результатом вынужденного конвективного теплообмена с импульсным плазменным потоком. Поэтому определение температуры частиц непосредственно перед моментом взаимодействия с основой представляет важную технологическую задачу.

Методика определения температуры частиц в потоке напыления включает измерение интенсивности излучения при разложении в спектр. При этом во время измерения производят суммирование спектральных интенсивностей на N длинах волн от пролетающих разнородно нагретых частиц конденсированной фазы. Получается суммарный тепловой спектр U от разнородно нагретых частиц, который является вектором значений U(l 1 ), U(l 2 ), …U(l i ),…U(l N ), где U(l i ) есть суммарная спектральная интенсивность, полученная на длине волны l i . Гистограмма Z температурного распределения частиц, которая представляет собой вектор значений на N заданных температурах, определяют по следующей формуле:

Z = A - 1 • U

,

где А – матрица размером N x N значений a ( l i , T j ) спектральной интенсивности излучения абсолютно черного тела, определяемых по формуле Планка на каждой из N длин волн и каждой из N заданных температур. Среднюю температуру частиц находят по формуле:

NN

T cp = T Z(T i ) • ^ TZ(T i )

I - 1               I I - 1          ,            (11)

где T ср – имеет вполне определенный физический смысл только для одномодовых распределений частиц Z(T i ) или может быть вычислена для совокупности нескольких локальных температурных распределений частиц.

В технологиях плазменного нанесения покрытий газовая фаза используется для транспортировки частиц конденсированной фазы к подложке. При этом газовая фаза обладает значительной температурой и имеет линейчатый спектр собственного излучения, в который входят линии излучения транспортирующего газа и незначительные следы линий излучения-поглощения испарившихся в процессе переноса мелких частиц порошка. Все нагретые частицы конденсированной фазы имеют непрерывный спектр собственного теплового излучения. В результирующем спектре U суммируются интенсивности излучения непрерывного теплового и линейчатого спектров, что делает невозможным определение точного температурного распределения Z по формуле (10) напрямую, с использованием формулы Планка для получения матрицы А.

Поставленная задача достигается благодаря тому, что в заданном сечении дважды производиться измерение интенсивности спектральных линий излучения плазменного потока, сначала без частиц конденсированной фазы в виде вектора значений S(l 1 ), S(l 2 ) ….,S(l i ),…, S(l N ) , а потом суммарного теплового и линейчатого спектра двухфазного плазменного потока U , из которого затем исключаются все значения на тех длинах волн l k , где интенсивность спектральных линий плазмы S(l k ) не равна нулю, а из матрицы A , полученной по формуле Планка, исключаются соответствующие столбцы и строки с элементами a ( l i , T j ) , где i и j равны k (рис. 2). Затем температурное распределение находится по формуле (10), а средняя температура частиц конденсированной фазы по формуле (11).

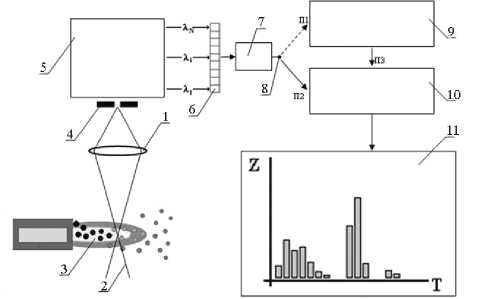
Рис. 2. Схема диагностики температурного распределения частиц конденсированной фазы в потоке плазмы:

1 – оптическая система; 2 – изображение сечения плазменного потока; 3 – двухфазный плазменный поток; 4 – входная щель спектрального дисперсионного устройства; 5 – спектральное дисперсионное устройство; 6 – фотоприемник из N элементов; 7 – аналогоцифровой преобразователь; 8 – переключатель режимов; 9 – блок выделения спектральных линий; 10 – блок цифровой обработки сигналов; 11 – гистограмма температурного распределения частиц)

Методика диагностики распределения скорости и температуры потока детонационного напыления реализована авторами в компьютерной автоматизированной системе ИСТ 2.4 [3]. Аппаратная часть системы состоит из светоприемников, которые расположены у среза ствола установки напыления. Они соединены оптическим волокнами с блоком оптоэлектронных преобразователей (ОЭП). Сигнал с блока ОЭП поступает на плату аналого-цифрового преобразования (АЦП), встроенную в компьютер посредством шины PCI. Работа АЦП и программной части диагностического комплекса синхронизована с установкой детонационного напыления.

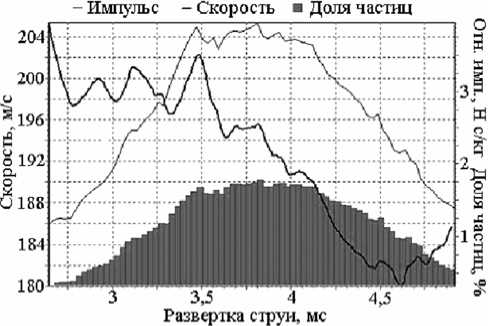
Рис. 3. Распределения скорости, относительной массы и импульса порошка в потоке за один цикл напыления

Автоматизированная система диагностики ИСТ 2.4 апробирована на установке детонационного нанесения покрытий «Катунь-М» [4]. В результате исследований удалось восстановить в каждом цикле напыления распределение средней по ансамблю скорости частиц с минимальной массовой долей ансамбля до 0,1%, что дало возможность анализировать параметры напыляемого порошка в различных частях потока детонационного напыления (рис. 3). Кроме того, эксперименты показали, что программно-аппаратный комплекс ИСТ

• 4. 2 при частоте работы установки напыления 8-10 Гц может осуществлять диагностику параметров конденсированной фазы потока в режиме реального времени и пригоден для работы в автоматизированных системах технологического контроля за процессом нанесения покрытий. Погрешность измерения скорости диагностической системой ИСТ 2.4 составляет 5%, а температуры 10%.

Выводы: методика измерения теплофизических параметров потока детонационного напыления, изложенная в данной статье, позволила создать способ диагностики распределения температуры и скорости частиц конденсированной фазы в процессе нанесения покрытий.