Физические теории пластичности: теория и приложения к описанию неупругого деформирования материалов. Ч. 3: теории упрочнения, градиентные теории

• 5.    Законы упрочнения в физических теориях пластичности

Изменение физико-механических свойств образца в процессах обработки металлов является следствием существенной перестройки микро- и мезоструктуры материала [10]. Описывать такие процессы невозможно без изучения и создания соответствующих моделей, в явном виде учитывающих физические первопричины эволюции микроструктуры материала при больших деформациях. Непосредственно в структуру физических теорий пластичности описание эволюции микроструктуры вводят через специфические соотношения (как правило, мезо- или микроуровня), определяющие изменение критических сдвиговых напряжений на системах скольжения в зависимости от некоторого набора параметров (в качестве которых могут выступать сдвиги, температура, энергия дефекта упаковки и т.д.). Известно, что даже незначительное изменение значений, входящих в закон упрочнения материальных параметров, может качественно отразиться на результатах описания поведения материала, в определяющие соотношения которого входят эти законы упрочнения, что говорит о необходимости очень тонкого и корректного учета механизмов неупругого деформирования материала, наиболее важных для исследования того или иного процесса.

В большинстве работ в рамках математических теорий пластичности, посвященных исследованию упрочнения, классификацию моделей последнего проводят исходя из качественного анализа вида кривой напряжение-деформация (получаемой в макроопытах) при продолжающемся активном нагружении и рассмотрения экспериментальных данных, полученных при исследовании микроструктуры материала при той или иной интенсивности деформаций [7, 9 и др.]. Так, в упрочнении часто выделяют стадии, наступающие последовательно при пластической деформации образца. Это стадия легкого скольжения, имеющая место непосредственно после достижения предела текучести материал; стадия линейного упрочнения, связанная, по-видимому, с пересечением дислокационных линий и формированием дислокационных структур; стадия параболического упрочнения, наблюдаемая у материалов с низкой энергией дефекта упаковки (ЭДУ) и связанная с взаимодействием уже не отдельных дислокаций, а образовавшихся на ранних стадиях дислокационных субструктур, а также с образованием и разрушением сидячих дислокаций [11]. Подобное рассмотрение, как представляется, едва ли можно использовать при построении физически обоснованной теории пластичности, так как, по сути, такая классификация представляет собой попытку описать упрочнение, основываясь только на макрофеномено-логическом подходе, не раскрывая при этом физических первопричин упрочнения и не опираясь на физику взаимодействия носителей механизмов пластической деформации - дислокаций и дислокационных субструктур.

Значительное внимание в физических теориях (как упругопластических, так и вязкопластических) уделяется модификации законов упрочнения в связи с новыми экспериментальными данными, полученными с применением высокоразрешающей аппаратуры (в особенности электронных микроскопов).

Краткий обзор существующих теорий упрочнения приведен в работе [58]; особое внимание уделяется теориям, основанным на рассмотрении эволюции дислокационных субструктур. Выделена модель [65, 66], в которой зерно представляется совокупностью блоков ячеек; для описания блоков вводятся ориентации потенциально возможных границ и присущие границам плотности дислокаций. Следуя указанным статьям, предлагаются эволюционные уравнения для плотности дислокаций, «налипающих» на границах блоков ячеек. Критические напряжения сдвига определяются по объемной доле границ блоков в зерне и накопленной плотности дислокаций. Входящие в эволюционные уравнения и выражения критического напряжения параметры модели предлагается определять методом наименьших квадратов по экспериментальным данным; приведены соответствующая постановка задачи оптимизации и алгоритм ее решения. Предлагаемый закон упрочнения был использован в самосогласованной вязкопластической модели для анализа деформирования при сложном нагружении поли-кристаллической меди (ГЦК-решетка). Сложное нагружение осуществлено по следующей схеме: образцы из отожженной меди прокатывались за один проход на 5,6, 10,5 и 18,8%, затем из них вырезались цилиндрические образцы в направлении прокатки, поперечном направлении и в направлении нормали к плоскости прокатанного листа. В дальнейшем полученные образцы подвергались осадке до деформаций от 24 до 44%. Для случая прокатки на 5,6 и 10,5% и последующей осадки предлагаемая модель показывает хорошее соответствие с экспериментальными данными; несколько худшее соответствие результатов имеет место при деформировании на первом этапе (прокат- ки) до 18,8%, в связи с чем авторы отмечают необходимость доработки модели упрочнения для описания IV стадии.

В большинстве современных исследований по упрочнению авторы используют так называемые дислокационно ориентированные модели ( dislocation based models ), в которых в качестве внутренних переменных микроуровня вводят скалярные плотности дислокаций на системах скольжения; далее записывают эволюционные уравнения для плотности дислокаций, а в качестве замыкающих уравнений записывают выражение, связывающее скорости сдвигов со скоростями изменения плотности дислокаций (обычно используется соотношение Оро-вана) [25, 30-33, 60, 72]. В качестве примера можно привести работу [32], в которой развивается именно такой подход. В части, касающейся описания упрочнения, авторы придерживаются классического подхода, когда скорость изменения критических касательных напряжений на системе скольжения записывается в виде

Nslip t g = Е Hgh Уh,                          (1)

h-I где tg - критическое напряжение сдвига на системе скольжения g, точка сверху означает материальную производную по времени, уh -скорость сдвига по системе скольжения h, Nip - количество активных систем скольжения, а коэффициенты (модули) упрочнения Hgh описывают взаимодействие дислокаций различных систем скольжения. Принимается гипотеза о том, что плотность дислокаций определяется тремя процессами: возникновения, скольжения и аннигиляции дислокаций при достижении достаточно большой плотности и продолжающейся пластической деформации. Эти механизмы учитываются в соотношении

Р g - ¹ ( ф - 2 У . Р g ] У g ,                      (2)

b V L J где рg - плотность дислокаций в g-й системе, b - модуль вектора Бюргерса, yc - расстояние аннигиляции для дислокационного диполя, Lg - длина свободного пробега дислокаций, определяемая, в свою очередь, соотношением g0

Z ph h=1, h * g где g0 - параметр, определяемый дислокационной структурой. Авторы [30] используют в качестве закона упрочнения соотношение

т

g c

= т₀ + ар b

^N slip

Z a ^- P h , h = 1

где т₀ - начальное критическое напряжение сдвига, а - параметр, связанный со стабильностью дислокационной структуры, р - модуль сдвига. Модули упрочнения H^gh тогда связаны с коэффициентами взаимодействия систем скольжения a ^gh соотношением

Н ^- =

ар

^N slip

2. Z a P ‘

V h = 1

a ^- I -1- - 2 у , p ^g

Попытка явного учета различных конкретных механизмов взаимодействия дислокаций в законе упрочнения делается в работе [72]. К существенным недостаткам предлагаемой модели следует отнести тот факт, что модули упрочнения в работе есть величины постоянные, а способ их определения не описан. Перечислим некоторые учитываемые в работе механизмы: формирование барьеров Ломера-Коттрелла, образование барьеров Хирта и так называемых «скользящих стыков», взаимодействие дислокаций на скрещивающихся системах скольжения, взаимодействие дислокаций, лежащих в одной плоскости, взаимодействие дислокаций одной и той же системы. Для скалярной плотности дислокаций принимаются соотношения вида (2) без учета размера зерна.

Следует отметить, что применение в качестве внутренних переменных скалярных плотностей дислокаций на системах скольжения влечет за собой большие сложности при использовании модели. Во-первых, использование переменных микроуровня сразу лишает исследователя возможности оперировать сколь-нибудь достоверными экспериментальными данными, дающими представление о реальных процессах, протекающих на данном масштабном уровне при пластической деформации; во-вторых, даже опираясь на геометрическую теорию дислокаций, едва ли можно учесть в уравнениях вида (2) взаимодействие дислокаций различных систем скольжения; наконец, в-третьих, даже в упомянутой достаточно простой модели введено множество материальных констант микроуровня, определять значения которых возможно только из экспериментов. В силу того, что состояние современной экспериментальной базы не позволяет в динамике отслеживать эволюцию дислокационных субструктур в объеме деформируемого материала, дислокационно ориентированный подход к описанию упрочнения представляется интересным и перспективным, но еще недостаточно инструментально оснащенным.

Заслуживает внимания также работа [15], в которой рассматривается трехмерная дислокационно ориентированная модель пластической деформации чистого алюминия. В ней для определения скоростей пластических сдвигов по системам скольжения вначале записывают модифицированное уравнение Орована как для винтовых, так и для краевых дислокаций; представляется странным учет движения винтовых дислокаций в уравнении Орована, хотя бы в силу особенностей движения винтовых дислокаций по сравнению с краевыми, в частности отсутствия систем скольжения для них как таковых. Для скалярной плотности дислокаций принимается гипотеза аддитивности скоростей генерации и аннигиляции дислокаций, скорости генерации как краевых, так и винтовых дислокаций принимаются не зависящими от направления скольжения.

Значения параметров упрочнения в соответствии с [72] разбиваются на несколько групп, исходя из типа взаимодействия дислокаций тех или иных пар систем скольжения (например, выделяют взаимодействия дислокаций разных систем, имеющих один и тот же вектор Бюргерса; систем с одной плоскостью скольжения; систем, склонных к образованию различных барьеров: Ломера-Коттрелла, Хирта, некоторых других).

В работе [51] рассматривается вязкопластическая модель, учитывающая влияние температуры, основанная на континуальной модели «механического порогового напряжения» (MTS - mechanical threshold stress), предложенной Фоллансби и Куксом [27]. Определяющие соотношения, используемые в данной модели, рассмотрены подробно во второй части обзора, здесь остановимся на особенностях описания упрочнения.

Критическое напряжение сдвига т ^ ) в рамках модели для учета влияния скорости деформации и температуры масштабируется «механическим порогом» т, представляющим собой сопротивление сдвигу при 0 К; последний разделен на атермическую т_а и термическую т\ составляющие, так что

^Т = ^T a + 2 ^{Т 1} •                          ⁽⁶⁾

l

Следует отметить, что использование термина «термическая составляющая» (введенного в исходной статье [27]) для второго члена правой части (6)) представляется не совсем корректным, поскольку «пороговое напряжение» т определено как сопротивление сдвигу при нулевой абсолютной температуре, а первый член правой части по определению не зависит от температуры 6.

Отмечается, что составляющая т_а характеризует нечувствительное к скорости взаимодействие дислокаций с дальнодействующими барьерами (например, границами зерен), а т l - чувствительные к скорости деформации взаимодействия дислокаций с близкодействующими препятствиями (например, дислокациями леса, примесными атомами), которые могут быть преодолены за счет термической активации. При изменяющихся температурах и скоростях деформации соответствующий вклад в критическое напряжение сдвига т l связан с его исходным аналогом т l масштабирующей функцией S l (D e ,6) , так что т l = т l S l (D e , 6) .

Критическое напряжение сдвига для всех СС определяется аналогично «механическому порогу»:

ll

> = > + 27 = > + 2 Sl (В»6) ^.(7)

G G l G G lG

Здесь G0 - некоторое отсчетное значение модуля сдвига G, определяемого соотношением

G = G(6) = Go--6 0      ,(8)

exp I % I-1

D_o, 6 0 - экспериментально определяемые константы.

Для описания кинетики взаимодействия на короткодействующих препятствиях используется соотношение Аррениуса и феноменологическое выражение для свободной энергии как функции напряжений, тогда каждая компонента т\ может быть записана в виде

l

т,

ˆ

т

"7 = S (d , , 9 ) -^ = 1

G

G

^^^^^^в

щ-.

I g o Gb 3    d u J

^

^т t

G 0

.

Здесь к - константа Больцмана, b - модуль вектора Бюргерса, g ₀ - нормализованная энергия активации дислокаций для преодоления препятствий, d _и о - константа, p , q - константы, характеризующие форму препятствий ( 0 <  p <  1, 1 <  q <  2 ).

В стандартной MTS-модели используются два термических члена, обозначаемые как т\ = тi, тt2 = тЕ, тогда соотношение (7) перепи шется в виде

/V                                         /V/V

2c

G

т                 т.т

S (d_M, 9 )^ + S (d_M, 9 )^,

G         G0

где

S -(d „ , 9 ) =

^^^^^^в

к 9

V g о i ^{G b 3}

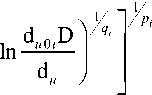
D ln- e^

S е (D e , 9 ) = 1

( к 9

^^^^^^в

V g 0е ^{G b 3}

^D e J

.

В этих соотношениях т i описывает термическую составляющую сопротивления деформации (в цитируемой работе этот член не учитывается), ат _Е - взаимодействие подвижных дислокаций с лесом дислокаций (учитывается).

Эволюционное уравнение для тЕ в скоростях записывается в следующей форме:

KK

--Е = h (9,d ,, тЕ )S| ?“'| = (h0 - hr (9,d u, тЕ) )Е|ТИ|.        (12> dt                   k=1                                    k=1

где h 0 отражает упрочнение, обусловленное накоплением дислокаций (принимается постоянным), а h r описывает скорость динамического возврата. Наиболее употребимыми функциональными формами скорости упрочнения h являются запись через гиперболический тангенс (Фоллансби-Кукс) или в виде степенного закона (Кукс и др.):

h = h ₀

^^^^^^^в

tanh

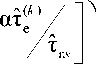
tanh(a)

h

G

h ₀

G 0

С

1"к

Т ( k ) Т

А ты 7

,

к

где a, к - эмпирические константы, т_ы - пороговое напряжение насыщения. В обоих соотношениях h 0 описывает начальную скорость упрочнения; скорость упрочнения h с ростом деформации уменьшается и стремится к насыщению. Применение подобных моделей для деформаций, превосходящих единицу, исключено, так что невозможно описать IV стадию упрочнения.

Пороговое напряжение насыщения ты является функцией скорости деформации и температуры:

ln-d u- = g ^{0E S} Gb In-b-, d u 0 _E          ^к 6        ^T = s 0

где d u _0e , g _{0e s} , т_ы 0 - эмпирические константы.

Верификация предлагаемой модели осуществлена сопоставлением полученных с ее помощью результатов расчета напряжений с результатами стандартной изотропной модели MTS. Скоростная и температурная зависимости определялись в опытах на сжатие алюминиевого сплава Al 5182 при температурах 200 и 300 °С при скоростях деформации 0,001 и 1,0 с-1. Показано очень хорошее соответствие результатов. Анализ предсказания моделью формирования текстуры осуществлен сопоставлением с результатами, полученными Kalidindi e.a. с использованием модели Тейлора; отмечается хорошее качественное соответствие результатов.

.к = - 2G(1 - Р)-----¹---- -(е p - Е ^p )

p

1 + ¥g ^£ u

/2 G где £U, оu - интенсивности пластических деформаций и напряжений. С учетом предположения о деформировании стенок ячеек упругим образом последнее соотношение модифицировано к виду

рк=- 777-G(1 - р)-------г Е ^(nm+mn), fw      1 + %G и

7 2   0 u где fw - объемная доля границ ячеек. Результаты расчетов сопостав лялись с данными экспериментальных исследований разных авторов, проведенных на растяжение и циклическое нагружение монокристаллов, показано удовлетворительное соответствие экспериментальных и теоретических результатов, полученных с помощью модифицированной модели. Результаты расчетов по модели Kroner на один-два порядка превышают экспериментально измеренные.

Интересный вариант физической модели упруговязкопластично-сти предложен в работе [52], согласно которому монокристалл представляется совокупностью «жестких» (зоны с повышенной плотностью дислокаций, например, стенки ячеек) и «мягких» (зоны с пониженной плотностью дислокаций, например, внутренность ячеек) областей.

Принимается гипотеза Фойгта; напряжения определяются суммой напряжений в «жестких» и «мягких» областях. В каждой из областей для упругой составляющей тензора деформаций используется изотропный закон Гука с отличающимися константами Ламе. Принимается гипотеза об аддитивном разложении тензора малых деформаций на упругую и вязкопластическую составляющие. Неупругие деформации осущест- вляются сдвигом в активных системах скольжения, условием активации является выполнение закона Шмида. Для каждой из областей скорости сдвигов в к-й СС определяются степенным законом вида

( k )        ( k )

' ( 5 )     П 5 )

( k ) ⁿ

Т2-

V Lc° )

( k )     ⁿ

^Т ( H )

sign(T ( k _:) ), у ( ^к _:) = H^   sign(T < H ) ) ,

VTC )

где индексы 5 , H относятся соответственно к «мягкой» (soft) и «жесткой» (hard) зонам, t_c0 - постоянное критическое напряжение в «мягкой» области, т С ^к ) - критическое напряжение сдвига в «жесткой» области, т ( 5 ) , т ( kk ) - сдвиговые напряжения в к- й СС, n - показатель скоростной чувствительности. Для критического напряжения сдвига в «жесткой» области т С k ) предлагается эволюционное уравнение, учитывающее активное и латентное упрочнение за счет сдвигов в обеих областях и возможное разупрочнение за счет сдвигов в «мягкой» зоне.

Предложенная модель была использована для анализа поведения монокристаллов при непропорциональном циклическом нагружении (траектории деформирования - круговые, в виде квадрата, 8-лучевой звезды), отмечается удовлетворительное качественное соответствие экспериментальным данным.

Модификация упруговязкопластической модели, учитывающая наряду со сдвиговой модой деформирование двойникованием, предложена в [46]. Для скоростей сдвигов и скорости изменения объемной доли двойников использован степенной закон с одинаковым показателем степени; для двойникования предполагается наличие предельной доли двойников, запрещен обратный переход. Градиент скорости перемещений для зерна определяется как сумма трех составляющих: скоростей сдвига в исходной матрице, скорости двойникования и скорости сдвига в сдвойникованной области, взвешенных с объемными долями каждой зоны. Для упрощения процедуры интегрирования соотношения записываются в неизменной отсчетной конфигурации.

Приведены примеры расчета текстуры для ГЦК- и ОЦК-поликри-сталлов; из сопоставления с экспериментальными данными следует, что неучет двойникования ведет к качественно неверным результатам. В [47] описанная модель расширена включением еще одной моды деформирования - микрополос сдвига. Применение данной модели к ГЦК-поликристаллам с низкой энергией дефекта упаковки позволило описать четыре стадии кривой упрочнения; отмечается необходимость учета образования микрополос сдвига для корректного предсказания эволюции текстуры.

Детальному описанию законов упрочнения ГЦК-кристаллов посвящена статья [45]. Рассмотрение кинематического и изотропного упрочнения монокристаллов основано на тщательном физическом анализе взаимодействия дислокаций различных СС. Использовано гипоуп-ругое соотношение, в котором коротационная производная тензора напряжений определяется по тензору спина решетки. Спин решетки полагается равным разности тензора вихря и антисимметричной части тензора скоростей сдвига по СС. Скорости сдвига в СС устанавливаются с помощью вязкопластического закона (произведение степенной и экспоненциальной функций сдвиговых напряжений).

Реализация модели осуществлена с применением МКЭ (пакет ABAQUS, 8-узловые симплекс-элементы); рассмотрен образец из монокристаллической меди, подверженный одноосному растяжению с постоянной скоростью роста напряжений. С позиций взаимодействия дислокаций тщательно описывается и анализируется упрочнение в первичной и вторичных СС. Сопоставление с экспериментальными результатами позволяет заключить, что предлагаемая модель хорошо описывает упрочнение на первых двух стадиях пластического деформирования.

В работе [20] рассматривается модель пластичности кристаллов, основанная на введении тензора плотности и/или скалярной плотности дислокаций. Во втором случае предлагается использовать вязкопластический закон: при выполнении условия Шмида на некоторой системе скольжения скорость сдвига в ней определяется соотношением

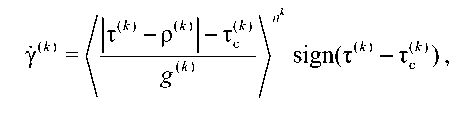
у ⁽ k )

Т ⁽ k ) - р ⁽ k )

sign(T ^k ) - т С ^k ) )

где т ^{( к} ) = M (k ) : о - сдвиговое напряжение в системе скольжения к , M S ') - симметричный ориентационный тензор, т С ^к ) , р ^{( к} ) - параметры изотропного и кинематического упрочнения, зависящие от плотности дислокаций; g ^{( к} ) , n - материальные константы, ^X^ = Max (0, X). Подробно закон упрочнения рассмотрен в [23] и имеет вид

^{( к} ) _ ^{( к} ) I Х' nkh ( 1 ^-b ^b r ^YC ™ V^{( r} ) — Г I V^{( r} ) I H

^T c = ^T 0 ⁺ ^ Q h r ^ ^{1 -} e      ) , Y cum ” | |Y |d t ,         ⁽¹⁶⁾

r

р(к) = скак, ак = у(к) - dкак у(к) - Г рк' ] mk sign (ак), (17) N X > где матрица |_Qkhkr J определяет активное и латентное упрочнение (неизотропный закон упрочнения), br, dк, mk, N - материальные константы.

Отмечается, что в работах Флека и Хатчинсона, Фореста с соавторами данная модель расширена включением кривизн-кручений кристаллической решетки, связанных с формированием дислокационных субструктур; в законе упрочнения появляется добавочный член, пропорциональный кривизне плоскости скольжения. Отмечается существенное влияние модуля упрочнения за счет кривизны решетки на напряженно-деформированное состояние в окрестности кончика трещины в монокристалле. К сожалению, объяснений, почему кривизны-кручения должны приводить к дополнительному изотропному упрочнению, не приводится; как представляется, более важным является появление моментных напряжений и несимметрии тензора напряжений, которые в модели не рассматриваются.

Весьма подробно вопросы построения и применения физических моделей упруговязкопластичности для описания поведения поликристаллов в широком диапазоне скоростей деформации (10-102 с-1) при больших деформациях (порядка 100%) и относительно низких гомологических температурах (Тг<0,3) рассмотрены в статье [18]. Как и в большинстве рассмотренных выше работ, использовано мультипликативное разложение градиента места и ОС анизотропной гиперупругости (с учетом температурной деформации), в котором в качестве мер напряженного и деформированного состояния приняты соответственно второй тензор Пиола-Кирхгоффа и тензор деформаций Коши-Грина, определенные в терминах разгруженной конфигурации.

Пластическое деформирование полагается реализующимся скольжением краевых дислокаций; следует отметить, что, как и во многих других работах последнего десятилетнего периода, закон вязкопластичности выводится на основе уравнения Орована

• ⁽ k) = p m ) bv ⁽ k ) {т k ) , ^ ) , ₀), , ₍₁₈₎

где p ^ ) - плотность мобильных дислокаций, v⁽k ) - средняя скорость движения дислокаций в к- й СС, причем v⁽ k ) равна нулю при |т ⁽ k )| <  т⁽_с ^к ) . Критическое напряжение сдвига полагается равным сумме двух составляющих: сопротивления близкодействующих барьеров, которые могут быть преодолены за счет термических флуктуаций даже при напряжениях ниже барьера Пайерлса-Набарро (называемого термической составляющей) т )к ) и сопротивления дальнодействующих барьеров (называемого атермической составляющей) т . к ) (см., например, [27]). Для модуля средней скорости движения дислокаций принимается соотношение

Ат ⁽ k ) <  0,

l ⁽ k ) v exp

( . ( к 0

k                   7

0 <  Ат ⁽ k ) <  т ^(к ) ,

где Ат ⁽ k ) = |т ⁽ k ) - т . k ) , l^(к ) - средняя длина свободного пробега дислокаций, v - характеристический частотный параметр (порядка 10¹² с^-1), у ⁽ k ) - свободная энтальпия активации (или свободная энергия активации Гиббса); направление движения совпадает с направлением сдвиговых напряжений. Предлагается модификация закона упрочнения, рассмотренного выше [62], для учета влияния температуры и скорости деформации.

Для определения макронапряжений используется процедура осреднения Тейлора по представительному объему, включающему 400 зерен. Предлагаемая модель встроена в конечно-элементный пакет ABAQUS. Подробно описаны процедура и результаты идентификации модели, выполненной для чистого (99,987 %) алюминия и алюминиевого спла- ва (ГЦК-решетка). Для идентификации использованы известные в литературе экспериментальные данные по одноосному растяжению образцов при нескольких значениях постоянных скоростей деформаций и температур. Полученные параметры были далее применены для теоретического предсказания поведения материала при одноосном нагружении со скачками по скорости деформаций и температуре; режимы изменения скоростей деформаций и температур выбраны аналогичными реализуемым в известных из литературы экспериментах. Сравнение расчетных и экспериментальных данных по зависимостям напряжение-деформация показывает хорошее соответствие.

В работе [70] описана упруговязкопластическая модель, в которой наряду с дислокационной сдвиговой модой деформирования учитывается двойникование. Используется гипотеза аддитивности упругой, дислокационной сдвиговой и двойниковой составляющих тензора деформации скорости; для двойников сдвиг полагается постоянным, соответствующая составляющая деформации скорости определяется скоростью изменения объемной доли двойников. Модель применена к анализу деформирования образцов из стали аустенитного класса (ГЦК-решетка). Вкладом двойникования в повороты пренебрегается; скорость поворота решетки определяется разностью тензора вихря и антисимметричной части дислокационной скорости сдвига. Дислокационная скорость сдвига на к -й СС определяется соотношением

у ⁽ k )

( ехр

V

A F кё"

(

V

^^^^^^^е

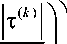
т ( k )

^с У?

sign ( т ⁽ k ) ) ,

где у₀- материальный параметр, A F - энергия активации преодоления барьеров (в отсутствии напряжений), к - постоянная Больцмана, 0 -абсолютная температура.

Упрочнение по СС определяется плотностью дислокаций; приведено эволюционное уравнение для скорости изменения плотности дислокаций, которая пропорциональна скорости сдвига и уменьшается при увеличении длины свободного пробега дислокаций. Длина свободного пробега зависит от среднего диаметра зерна, расстояния между двойниками и плотности накопленных дислокаций. Средний размер пакета микродвойников полагается постоянной величиной (30 нм), число микродвойников в пакете в соответствии с экспериментальными данными принято равным 5. Кинетическое уравнение для объемной доли двойников записано в виде степенной зависимости от отношения напряжения сдвига по системе двойникования к критическому напряжению двойникования. Для связи параметров мезо- и макроуровней используется самосогласованная модель.

Предлагаемая модель использована для исследования поведения поликристаллического образца при одноосном растяжении; описана процедура идентификации модели. Результаты расчетов показывают, что вклад двойников в неупругую деформацию мал (около 3%); однако, являясь эффективными препятствиями для дислокаций, появление двойников ведет к значительному упрочнению. Двойникование имеет место в 90 % зерен представительного макрообъема, причем в большинстве зерен доминируют две системы двойникования. Объемная доля двойниковых пакетов растет с ростом деформации, составляя 6 % при деформации 0,3. Результаты расчета обнаруживают удовлетворительное соответствие экспериментальным данным.

В работе [57] приведено краткое описание эволюции микроструктуры при деформировании ГЦК-монокристаллов (ячейки, блоки ячеек, субзерна, дислокационные стенки, разделяющие ячейки и блоки). Для описания микроструктуры предлагается ввести внутренние переменные, моделирующие блоки ячеек и дислокационные стенки. В качестве основного ОС используется закон Гука, записанный для разгруженной конфигурации. Скорости сдвигов по СС определяются из закона Орована; скорость движения дислокаций устанавливается кинетическим законом, учитывающим энергию активации дислокаций, температуру, сдвиговые напряжения, плотности мобильных дислокаций и дислокаций леса. Основываясь на принципе максимума работы напряжений на пластических деформациях, стало возможным получить выражение для плотности мобильных дислокаций; представляется странным, что плотность мобильных дислокаций принимается пропорциональной корню квадратному плотности дислокаций леса. На основе того же принципа для случая «композита» из блоков ячеек и стенок выведено выражение для плотности мобильных дислокаций как функции плотностей дислокаций в блоках ячеек и дислокационных стенках. Предложены основанные на рассмотрении дислокационных реакций кинетические уравнения для изменения плотностей иммобильных дислокаций в блоках ячеек и в дислокационных стенках.

Для моделирования «композита» из блоков и стенок для каждой системы скольжения предлагается использовать модель Максвелла, в которой в силу сложности реализации пренебрегается упругими составляющими сдвигов. В итоге построенная модель имеет в своем составе десять материальных констант. Авторы отмечают, что вследствие построения всех кинетических уравнений на основе теории дислокаций указанные константы имеют ясно выраженный физический смысл и, по крайней мере, известен порядок этих величин. Авторами проведен физический анализ и обоснованы интервалы возможных значений каждой из констант, входящих в модель. Разработанная модель использована для анализа сжатия монокристалла алюминия при трех скоростях изменения приложенной нагрузки (0,2, 2 и 20 Н/с) и трех различных температурах (623, 673 и 723 К); сопоставление теоретических результатов с экспериментальными показывает удовлетворительное соответствие. Отмечается, что в дальнейшем модель предполагается расширить на более широкий температурный диапазон и ОЦК-кристаллы и встроить её в конечно-элементную программу.

Близкая к рассмотренной выше «композитная» упругопластическая модель для описания ячеистой структуры монокристалла рассмотрена в работе [77]. Материал представляется совокупностью ячеек и стенок (областей с повышенной плотностью дислокаций); записаны эволюционные уравнения для плотности дислокаций. Для моделирования используется теория течения с комбинированным законом упрочнения и гиперупругий закон, в котором второй тензор Пиола-Кирхгоффа определен в разгруженной конфигурации. На двухзвенных траекториях деформации (растяжение - растяжение с изломом траектории) анализируется влияние величины деформации первого участка траектории и угла излома на остаточные напряжения в ячейках и стенках; отмечается возможность применения модели для описания эффекта Баушингера. Результаты расчетов удовлетворительно согласуются с экспериментальными данными.

В статье [67] рассмотрена самосогласованная «композитная» упруговязкопластическая модель, согласно которой зерно поликристалла представляется совокупностью «мягкого» ядра и «жесткой» оболочки. В ядре учитываются только статистически накопленные дислокации (СНД) (с нулевым суммарным вектором Бюргерса), тогда как в оболочке наряду со СНД важную роль играют геометрически необходимые дисло- кации (ГНД), обеспечивающие совместность деформаций по границам неоднородно деформируемых зерен. В каждой из двух зон тензор деформации скорости представляется суммой упругой и вязкопластической составляющих; для упругой составляющей используется изотропный закон Гука, для вязкопластической - степенной закон течения.

Напряжение течения определяется плотностью дислокаций; для плотностей СНД и ГНД приведены эволюционные уравнения. Для связи переменных мезо- и макроуровня использована самосогласованная схема (Эшелби), для упрощения анализа форма зерен считается сферической. Модель применена для исследования поведения стали ферритного класса с различными средними размерами зерна (5,5, 8,5, 15, 120 мкм). Модель хорошо описывает зависимость напряжения течения от размера зерна; показано, что в приграничной зоне внутренние напряжения существенно превышают напряжения в ядре зерен. Показано существенное влияние размера зерна на уровень остаточных напряжений второго рода (на мезоуровне). Все результаты расчетов хорошо согласуются с экспериментальными данными.

Модификация упруговязкопластической модели, основанная на прямом рассмотрении движения краевых и винтовых дислокаций, предложена в работе [15]. Скорость сдвига в каждой СС определяется плотностями соответствующих типов дислокаций и средними скоростями их движения (т.е. по уравнению Орована). Предложены эволюционные уравнения для плотности дислокаций, учитывающие их генерацию (источниками Франка-Рида) и аннигиляцию. Критические напряжения сдвига в СС определяются отдельно для краевых и винтовых дислокаций по плотности дислокаций обоих типов, накопленных в других СС, и законам взаимодействия с ними (с учетом образования барьеров дислокационного типа). Ротации решеток зерен устанавливаются ортогональным тензором, входящим в полярное разложение упругой составляющей градиента места. Подробно описана численная процедура реализации модели. Вышеописанная физическая модель была встроена в конечно-элементный пакет ABAQUS. Для идентификации использованы экспериментальные данные по растяжению монокристалла алюминия. Представлены результаты расчета прямых полюсных фигур при стесненной осадке (в условиях ПДС) образцов из поликристаллического алюминия.

В работах [11, 12, 14, 76] предлагается подход к описанию упрочнения в моно- и поликристаллах, связанный с физическим анализом механизмов взаимодействия дислокаций друг с другом и с границами зерен. Дается краткий обзор существующих в отечественной и иностранной литературе теорий упрочнения. Отмечается, что существуют два основных варианта построения таких соотношений: первый - без явного учета эволюции дефектной структуры материала, второй - на основе подхода к построению определяющих соотношений с использованием внутренних переменных, характеризующих микроструктуру материала; при этом, как правило, необходимо использовать переменные микроуровня - плотности дислокаций, что приводит к проблеме замыкания эволюционных уравнений.

Рассматриваются некоторые физические механизмы упрочнения, предлагается разделение упрочнения на неориентированное и ориентированное. Первое описывает упрочнение независимо от направления деформирования (образование пересечений дислокаций, жгутов, кос, барьеров Ломера-Коттрелла); такое упрочнение приводит к увеличению критического напряжения сдвига сразу на многих СС. Второе связано с накоплением упругой энергии на «поджатых дислокациях» (на различных барьерах), эта энергия может высвобождаться при «развороте» направления деформирования. Запасаемая на микродефектах энергия, в свою очередь, разделяется на два типа: не высвобождаемая на микро- и мезодеформациях и высвобождаемая; доля «высвобождае-мости» зависит от сложности нагружения. Это разделение учитывается, например, при модификации основного (степенного) составляющего закона упрочнения и при описании эффекта Баушингера.

В предположении об аддитивности скоростей критических напряжений сдвига на системе скольжения, обусловленных различными механизмами упрочнения, основной закон упрочнения дополняется слагаемыми, учитывающими основные механизмы возникновения препятствий при пластическом деформировании, не учтенными первым (степенным) слагаемым.

Подход к описанию неориентированного упрочнения иллюстрируется на примере описания дополнительного упрочнения за счет образования барьеров Ломера-Коттрелла. Определяются внутренние переменные, дополнительная функция упрочнения f ЛК1 принимается в виде fж1 ( Уэду, y (°, У (j) ) =

= ⁵ 1 ^Г

⁽ i ⁾

c

(

1 -

V

У н 1

У* эду 7 V

У* эду J

( t,          „л^-1

j f .' d Г + f ' i ⁾

V о              7

N *

У ⁽ⁱ⁾ Z y ^{( j )}

V j * i

. 7

+ У о

где у Эд _У - критическое значение энергии дефекта упаковки (ЭДУ) материала, у_ЭДУ - ЭДУ материала, N * - число СС, сопряженных к данной, г С ⁾ - текущее критическое напряжение, у 0 - малая константа, 5 1 - материальная константа, Н - функция Хэвисайда.

Рассматривается ориентированное упрочнение за счет аннигиляции дислокаций, «поджатых» на препятствиях, при смене направления деформирования, а также за счет взаимодействия внутризеренных дислокаций с границами зерен в случае деформирования поликристалла. Подробно рассмотрены физика процесса аннигиляции и факторы, влияющие на уменьшение критического касательного напряжения на данной СС в результате аннигиляции дислокаций. Для учета высвобождаемой упругой энергии в соотношение для f £) введен дополнительный множитель, учитывающий сложность нагружения по всем СС:

( ‘ )                       v( ‘ )

f ⁽ i )                      d¹™ ₌_£ _T⁽ i ⁾ _^У---- y⁽ i ) ⁽ i ^{+ 12)} _{+        T} ^{( i )}

. f ан ^{( p}1 , ^p 2 , — , ^p m ) d i ⁵ 2 ^Ган ^ ( j ) ^У ( ^{У T У}0 ) , ^Ган

1 1 =0

= Г d i = 1,24, где Z У(j) - суммарный накопленный сдвиг, у“ - малый параметр, 52 - материальная константа.

При описании зернограничного упрочнения принимается модель прохождения дислокации через границу с образованием в ней дислокации ориентационного несоответствия. Дополнительное зернограничное упрочнение описывается при помощи соотношения fй■ (yw, У(i), 5 )=чу") У 'i^Sk ^« • к=1 V0

где Sk - площадь зерна, «приходящаяся» на данную СС, V0 - объем зерна, P - количество плоских участков, аппроксимирующих границы зерна, мера разориентации §jk определяется по минимальному значению для рассматриваемой СС данного зерна j, плоского участка гра ницы к и всех СС 1 соседнего зерна: §jk = min ^n(к) {b( 1) - b(j) )}, где n(k)

–

нормаль к плоскому участку границы.

Проведена серия численных экспериментов по деформированию моно- и поликристаллов с учетом различных дополнительных слагаемых в законе упрочнения. Удовлетворительно описано начало второй стадии упрочнения, связанное с введением в законы упрочнения слагаемого, описывающего дополнительное упрочнение за счет реакций на расщепленных дислокациях и образования барьеров Ломера-Коттрелла. Представлены результаты по реверсивному деформированию с учетом слагаемого, описывающего аннигиляцию дислокаций. Для модельного материала (чистая медь) показано, что при смене направления деформирования (с одноосного растяжения на одноосное сжатие в том же направлении) предел текучести материала снизился с ~ 33 МПа до ~ 30 МПа.

Проведены численные эксперименты по циклическому деформированию: представительный объем поликристалла подвергали кинематическому нагружению (растяжение-сжатие) при различном числе циклов нагружения. С увеличением количества циклов отчетливо проявляется эффект Баушингера, наблюдается явление «размывания» второй стадии упрочнения по всему участку пластического течения. Исследование изменения дефектной структуры материала при большом числе циклов показывает на постепенный выход всех СС на одинаковую плотность барьеров Ломера-Коттрелла. Приведена диаграмма одноосного сжатия поликристалла при учете слагаемого, описывающего зернограничное упрочнение. Заметен переход с некоторого момента деформирования от линейного упрочнения к нелинейному участку; нелинейность обусловлена совместным влиянием на скорость дополнительного упрочнения как скорости сдвига по данной СС, так и накопленного сдвига по этой же СС (в отличие от других дополнительных слагаемых).

• 6.    Модели обобщенных континуумов

В последние годы для модификации различных физических теорий исследователями все чаще применяются модели обобщенных континуумов (градиентные теории - в особенности). Остановимся деталь- нее на некоторых работах данного направления. В статье [71], основанной на феноменологической градиентной теории пластичности [26], рассматривается вариант градиентной физической теории упруговяз-копластичности. Анализируется случай малых градиентов перемещений, в связи с чем не делается различия между отсчетной и актуальной конфигурациями. В духе микроморфного континуума Миндлина [61] вводятся радиусы-векторы макроточки X и микроточки х, соответствующие операторы Гамильтона обозначим как V и □. Каждой макроточке X приписывается микрообъем 5 V, наделенный микроструктурой (системами скольжения). Скорости сдвига по произвольной к-й СС определяются разложением в ряд Тейлора с сохранением градиентов первого порядка:

у ^{( к} ) ( X , x ) = (у⁽ k )) ( X ) + x ( Пу ⁽ kУ ( X ) , (20) где ^у⁽ k )^ ( X ) - осредненная по 5 V скорость сдвига по к -й СС, ^Пу ^{( к} )^ ( X ) - осредненный по 5 V градиент скорости сдвига по к -й СС. Пластическая составляющая тензора деформации скорости далее определяется обычным соотношением

D p = d p = ^ у ^{( к} ) ( X , x ) M ^{( к} ) . (21) k

Подстановка (20) в (21) и запись мощности напряжений в единице 1

объема на скоростях пластических деформаций, N p =      о : d p d V ,

5 V 5JV приводит к следующему результату:

N p = 0 :(d p ) + (т) • (ч p ),                   (22)

где (d У = Е(у^{( к} ^( X ) M^{( к} ) , (ч p ) = Ем^{( к} )( °у ^{( к} )) ( X ) , 0 = — Jo d V , 5 V 55,

(т^ =— Jo x dV, A • B = A^Bj; тензор (третьего ранга) (ч) называ-' '    5 V 8JV ется тензором «парных напряжений».

Тензор скорости полных микродеформаций в 5 V полагается линейной функцией микрокоординат х . Тогда мощность напряжений на единицу объема можно представить соотношением

N = ^ J °:D d V = (°) :(D + (t) • ^), ⁸ V ₈ V

где (D) = —  D d V , (А) =

8 V

—— J D 0 dV. В дальнейшем полагается, что 5 V 8*V осредненный по 8V тензор скорости микродеформаций ^D^ равен тензору скорости макродеформаций А в точке X, А (X) = ^D^, а DV = (А). Уравнения равновесия и статические граничные условия макроуровня получены на основе принципа виртуальной мощности. В качестве определяющих соотношений макроуровня использован закон Гука в скоростной форме как для напряжений, так и для парных напряжений:

й) = C:De,   (t) = le2 C: (Ae), где lе - параметр, имеющий размерность длины и связанный с размером области 8 V («упругий масштаб»), С - обычный тензор упругих характеристик (4-го ранга).

На микроуровне используется модифицированная модель вязкопластичности. С этой целью вводятся эффективная скорость сдвига и эффективные сдвиговые напряжения для каждой СС, включающие в себя соответственно градиенты скоростей сдвигов и парные напряжения, с помощью масштабных коэффициентов приведенные к размерности скорости сдвига и обычного напряжения. Закон упрочнения по СС определяется в терминах эффективной скорости сдвига. Принимается степенной закон зависимости эффективной скорости сдвига от эффективного сдвигового напряжения на каждой СС. Модель замыкается гипотезой о равенстве отношений средних по СС скоростей сдвигов и их градиентов (последние умножаются на масштабные факторы) и соответствующих энергетически сопряженных силовых факторов на каждой СС, причем это отношение равно отношению эффективной скорости сдвига к эффективному напряжению сдвига в каждой СС. Приведены результаты решения модельной плоской задачи о деформировании бикристалла; анализируется влияние на результаты параметров модели (в частности, масштабных факторов).

В статье [24] градиентная модель основана на концепции «геометрически необходимых дислокаций (ГНД)» (восходящей к работам [17, 50, 64]; детальное рассмотрение теории ГНД, определение тензора их плотности через Fр и градиент Fр в отсчетной конфигурации содер- жится в [21]). Согласно этой концепции, наряду со «статистически накопленными дислокациями (СНД)» [17], являющимися следствием однородного пластического деформирования, вблизи областей неоднородности пластических сдвигов (например, в окрестности границ зерен) появляются дислокационные субструктуры типа стенок дислокаций, дислокационных ячеек и т.д., которые должны обеспечить совместность деформации решетки и отвечают за искривления - кручения решетки, которые и называются «геометрически необходимыми дислокациями».

В соответствие с указанной концепцией авторы представляют поликристалл совокупностью двух «фаз» - примерно однородно деформируемых «ядра» зерен и зон, моделирующих участки границы каждого из зерен.

В качестве основы для описания поведения «зон однородности» принята упруговязкопластическая модель [48], основанная на мультипликативном разложении Ли, изотропном гиперупругом законе, в котором в качестве мер напряженного и деформированного состояния выбраны соответственно второй тензор Пиола-Кирхгоффа и тензор деформаций Коши-Грина, определенные в терминах промежуточной (разгруженной) конфигурации.

Основное отличие от известных моделей кристаллов заключается в упомянутой выше «двухфазности» материала. Поликристалл представляется совокупностью «ядер» зерен и приграничных областей -бикристаллов. При этом бикристаллические зоны подразделяются на две подобласти - «внутреннюю» и «внешнюю» (для каждого зерна), каждая из этих подобластей «наследует» ориентацию систем скольжения зерен, примыкающих к моделируемому участку границы. На границе подобластей задаются дополнительные условия совместности по градиентам места и напряжениям. Полные деформации в «ядре» зерен и осредненные деформации в каждом бикристалле полагаются равными осредненным деформациям (т.е. принята гипотеза Фойгта).

Напряжения в зерне определяются осреднением по объему «ядра» и бикристаллов, окружающих зерно (с учетом объемной доли «ядра» и бикристаллической границы). В представительном объеме напряжения определяются осреднением по совокупности зерен (сумма напряжений в зернах, деленная на число зерен, составляющих представительный объем).

Полагается, что ГНД накапливаются с ростом деформации во внутренней части бикристаллов, их плотность определяется разностью пластических составляющих градиентов места в ядре и внутренней части бикристаллов. Появление ГНД связывают с дополнительным (по отношению к увеличению критических напряжений за счет статистически накопленных дислокаций) упрочнением систем скольжения. Предлагаемая модель использована для анализа одноосного растяжения образца с акцентом на проверку справедливости соотношения Холла-Петча. Результаты расчетов по предлагаемой модели сопоставлялись с теоретическими результатами прямого конечно-элементного моделирования и экспериментальными данными для поликристалличе-ской меди со средним размером зерна 14, 33 и 220 мкм, показано их хорошее соответствие. Дальнейшее развитие данной модели на двухфазный материал (суперсплав на основе никеля) содержится в работе [75].

Построению физической теории, учитывающей наличие в деформируемом кристалле совокупностей дислокаций двух типов - СНД и ГНД - и основанной на термодинамическом подходе, посвящена работа [73]. Рассматривается случай малых градиентов перемещений, в силу чего системы скольжения полагаются фиксированными в отсчетной конфигурации. Наряду с мультипликативным разложением градиента места, скоростью пластической составляющей последнего, выраженной через скорости сдвига по СС, используется ротор и скорость ротора пластической составляющей градиента места, выражаемые линейными функциями скорости сдвигов и градиента скорости сдвигов. Вводится эволюционное уравнение для скорости суммарной (СНД+ГНД) плотности дислокаций, скорость изменения которой также представляется квазилинейной функцией скоростей сдвига и градиентов скоростей сдвига. Предлагается общая форма конститутивного соотношения, согласно которой отклик материала (например, тензор напряжений или свободная энергия) определяется независящей от выбора системы отсчета функцией температуры, тензора деформаций Коши-Грина, плотности дислокаций, градиента температуры, скорости сдвигов и градиента скорости сдвигов.

Рассматривается два метода вывода балансовых и конститутивных соотношений, основанных на термодинамическом подходе (в обоих используется неравенство Клаузиуса-Дюгема). В первом из них, названном моделью обобщенных внутренних переменных, сдвиги и градиенты сдви- гов вводятся в уравнение баланса энергии и энтропии неявным образом через зависимость от указанных параметров свободной энергии. Во втором методе - «модели внутренних степеней свободы» - скорости сдвигов явным образом вводятся в выражение для скорости изменения полной энергии и энтропии, при этом появляется необходимость в определении дополнительных параметров, термодинамически сопряженных с новыми степенями свободы.

Предлагается два способа определения плотности ГИД. В первом из них, называемом моделью системы скольжения, векторная мера плотности ГИД определяется для систем скольжения через градиенты сдвигов по ним. Во втором способе («континуальном») векторная мера плотности ГИД вводится через ротор пластической составляющей градиента места. Для каждого из этих способов получены эволюционные уравнения для скорости изменения меры ГИД. В дальнейшем плотности СИД и ГИД вводятся в качестве аргументов функции свободной энергии; установленные эволюционные уравнения для СИД и ГИД вводятся в структуру полученных на основе термодинамического подхода эволюционных и конститутивных уравнений. Для замыкания полученной системы уравнений требуется дополнительное соотношение, не вытекающее из термодинамики; в качестве такого уравнения используется экспоненциальная зависимость скоростей сдвигов по СС от энергии активации Гиббса и температуры. Описан алгоритм включения предлагаемых моделей в конечно-элементную процедуру.

Развитие предложенного подхода на случай больших градиентов перемещений содержится в работе [74]. Рассматривается общий вид термодинамических потенциалов (функции свободной и накопленной упругой энергии, диссипативная функция), приведена формулировка вариационного термодинамического принципа в скоростной форме. Значительная часть работы посвящена анализу работ по обобщенным физическим теориям пластичности, основанных на рассмотрении СИД и ГИД. Показано, что часть из предлагаемых моделей может быть получена как частные случаи предлагаемого в статье формализма.

Вариант градиентной модели вязкопластичности предложен в работе [34]. В мультипликативное разложение градиента места авторами вводится промежуточный член F g , переводящий пластически деформированную конфигурацию в промежуточную (разгруженную),

F = F e • F g • F p . Указанный член разложения связан с наличием ГНД и определяется по градиентам сдвигов в активированных СС; при этом ГНД порождают дальнодействующие поля внутренних напряжений. Скорости сдвигов в СС определяются степенным вязкопластическим законом, включающим как изотропное упрочнение, так и кинематическое, при этом оба члена в комбинированном законе упрочнения зависят от градиентов накопленных сдвигов. Детально описан алгоритм решения задачи. Для решения задачи на макроуровне применен МКЭ. Для анализа влияния градиентных членов рассмотрен пример одноосного циклического нагружения (растяжение-сжатие) образца из монокристаллического алюминия с сужением в центральной части. Отмечается, что учет градиентных членов ведет к более быстрому формированию шейки и повышению неоднородности пластических деформаций по образцу.

В последнее десятилетие весьма интенсивно работает над созданием градиентных физических моделей M.E.Gurtin с соавторами [19, 35-44, 53]. Остановимся подробнее на одной из последних работ этой группы исследователей [37]. Рассматривается случай малых градиентов перемещений, используется аддитивное разложение градиента скорости перемещений. Пластическая составляющая последнего определяется скоростями сдвигов по СС. В основу модели положен принцип виртуальной мощности. Наряду с обычными силовыми факторами (распределенными поверхностными и объемными силами, тензором напряжений Коши) в рассмотрение вводятся силовые факторы микроуровня: скалярное напряжение л^{( к} ) на к -й СС (сопряженное с соответствующей скоростью сдвига), вектор микроскопических напряжений ^ ^{( к} ) (сопряженная переменная - градиент скорости сдвигов), скалярная распределенная поверхностная нагрузка %^{( к )} , сопряженная со скоростью сдвига по к -й СС.

Формулируя принцип виртуальной мощности для произвольной части монокристалла (равенство мощности работы внутренних и внешних сил на виртуальных скоростях макро- и микроуровня), производя типовые преобразования с использованием теоремы Гаусса-Остроградского, авторы записали условия Коши и уравнения равновесия для макропеременных, а также соответствующие уравнения для микропеременных:

X ⁽ k ) ( n ) = § ⁽ k ) . n , div ^ ⁽ k ) + т ⁽ k ) - л ⁽ k ) = 0,

где n - единичная внешняя нормаль к рассматриваемой области, т⁽ k ) -сдвиговое напряжение на к -й СС. Для анализа физического смысла ^ ⁽ k ) в рассмотрение вводятся краевые и винтовые дислокации, залегающие в СС; плотность дислокаций выражается через градиенты сдвигов в СС. Вектор микроскопических напряжений ^ ⁽ k ) представляется суммой упругих и диссипативных напряжений, § ⁽ k ) = ^ ^ k ) + § d k ) . Из рассмотрения свободной энергии Гельмгольца, определенной как сумма энергии на упругих макродеформациях и энергии дислокаций, следует, что ^ ^к )

суть распределенные силы Печа-Колера на краевых и винтовых дислокациях.

Определяющие соотношения для диссипативных микронапряжений л⁽ k ) и ^ d k ) строятся по аналогии с физическими вязкопластическими уравнениями. Для этого вводится «эффективная скорость течения»

d^(к ) = ^| у ⁽ k )|² + 1 2 |v ^{( к} ) у ^{( к} )|

I , где V(к) - градиент, определенный в плоско- сти к-й СС, 1 - характерный масштаб. После этого диссипативные напряжения определяются следующими соотношениями:

у ( ^к ) „ (» = _т < k >  R ( dt > ) d_ ,

V ⁽ k )У⁽ k ) s d S = т k ) r ( d< ^{k )} ) i ^-L- , d ⁽ )

где R ( d ^{( k} ) )- индикаторная функция ( R (0)=0, R ( d ^{( k} ) )>0 при d ^{( k} ) ^0), т С ) - сопротивление сдвигу на к -й СС. Благодаря подстановке (26) в (25) в конечном счете получили закон течения, связывающий т ^{( к} ) со скоростями сдвигов, их первыми и вторыми градиентами на каждой СС. Приведены результаты решения тестовой двумерной задачи при различных параметрах упрочнения и характерных масштабах.

В работе [63] модель [40] в упругопластическом варианте применена для анализа деформирования тонкой (с толщинами 0,25, 0,5 и 1 мкм) пленки на упругом полупространстве. В начальный момент времени пленка и подложка нагреты до некоторой температуры, после чего система равномерно охлаждается; контакт предполагается идеальным, задача поставлена для условий ПДС; пластические деформации возникают вследствие разницы коэффициентов температурного расширения. В пленке существуют три СС, симметрично расположенные относительно нормали к поверхности. Симметрия СС и бесконечная протяженность пленки и подложки вдоль линии их сопряжения (в плоскости моделирования) позволяют перейти к краевой задаче для обыкновенных дифференциальных уравнений второго порядка относительно скорости сдвига; получено аналитическое решение редуцированной задачи. Результаты ее решения сопоставляются с данными, полученными авторами ранее с помощью методов дислокационной динамики.

В [78] для вывода разрешающих соотношений градиентной модели упруговязкопластичности используется принцип виртуальных мощностей и линейная неравновесная термодинамика (неравенство Клаузиуса-Дюгема). Особое внимание уделяется межфазным границам (в частности, границам зерен), играющим важную роль в описании поведения субмикро- и нанокристаллических материалов. Для описания различных механизмов неупругого деформирования и упрочнения предлагается разделить обобщенные термодинамические силы на «энергетические» (связанные с возрастанием энергии дефектов и сопряженные с пластическими деформациями и их градиентами) и «диссипативные» (описывающие диссипацию энергии и сопряженные со скоростями пластических деформаций и их градиентами). При этом возникает необходимость во введении четырех характерных масштабов - двух («энергетического» и «диссипативного») для внутренних областей кристаллитов и двух - для межфазных границ.

Вариант основанной на термодинамическом подходе градиентной упруговязкопластической модели предложен в [79]. Для ясности изложение ведется на примере одномерной модели; в качестве независимых термодинамических переменных используются упругие деформации, сдвиги по СС и градиенты сдвигов. Из неотрицательности диссипации энергии получен общий вид определяющих соотношений, устанавливающих форму зависимости сопряженных термодинамических сил и содержащих производные свободной энергии по термодинамическим переменным. Рассмотрены два варианта выбора функции свободной энергии, выпуклой и невыпуклой; в первом случае свободная энергия зависит от квадратов упругой деформации и градиента сдвига; во втором случае добавляется степенной ряд по величине сдвига (до четвертой степени включительно), отмечается аналогия данного подхода с моделью фазового поля Гинсбурга-Ландау. На численных примерах одноосного монотонного нагружения стержня показаны качественные отличия результатов, полученных с применением выпуклой и невыпуклой функции свободной энергии. В частности, для невыпуклой функции на диаграмме напряжение-деформация имеет место участок разупрочнения, наблюдается локализация пластических сдвигов; при этом результаты существенно зависят от скорости деформирования и граничных условий.

Обширный обзор работ по градиентным моделям физических теорий пластичности содержится в статье [59]. Значительной внимание уделяется мультипликативному разложению градиента места на разных масштабных уровнях (монокристалла и поликристалличе-ского агрегата) и связи его пластической составляющей с плотностью ГНД.

В последние 10-15 лет отмечается существенное повышение интереса к обобщенным континуумам типа Коссера [22], их обобщению на упругопластические среды и введение в физические теории пластичности [28-29]. В работах этого направления в духе континуума Коссера материальные частицы наделяются тремя дополнительными (к трансляционным) степенями свободы, которые обычно связываются с кривизнами-кручениями кристаллической решетки (которые, как и в градиентных моделях, порождаются геометрически необходимыми дислокациями); вводится энергетически сопряженный тензору кривизн-кручений тензор моментных напряжений. Для тензоров деформаций и кривизн-кручений (или их скоростей) часто принимается аддитивное разложение на упругую и пластическую составляющие. Для определения неупругих деформаций и искажений кристаллической решетки применяются вязкопластические законы, связывающие соответственно скорости сдвигов и поворотов с тензором напряжений Коши и тензором моментных напряжений. Модифицированная физическая модель использована для исследования устойчивости пластического деформирования монокристаллов, анализа поведения одно- и двухфазных поликристаллических материалов при различной величине среднего размера зерна.

В работе [49] рассматривается модификация вязкопластической модели [16, 62]. Описание трансляционной моды деформации анало- гично принятым в большинстве работ (мультипликативное разложение градиента места, степенной вязкопластический закон); при этом упругими деформациями пренебрегается и упругая составляющая градиента места полагается ортогональным тензором. Выделяются симметричные и антисимметричные части скоростей сдвигов и напряжений Коши. Из уравнения момента количества движения в пренебрежении массовыми моментами следует

2° (A)+ е<^7 • р) = 0, где °(A) = 12 (° _ °T ) — антисимметричная часть тензора напряжений Коши, р - тензор моментных напряжений. Получено следующее выражение принципа виртуальной мощности:

j°(S): 5DdV + jр: 5/dV = jt • 5vd5 + Jр • Sod5,(28)

V    VSS где °(S)- симметричная часть тензора напряжений Коши, o - вектор скорости «материального поворота» (ассоциированный с тензором вихря W), / = VoT , t - вектор поверхностных сил, р - вектор поверхностных моментов. Для понижения порядка аппроксимации предлагается модификация уравнения (28), в которое вводится добавочный поверхностный интеграл, позволяющий учесть разрывы в моментных напряжениях на границах элементов. Приведен вывод конечноэлементных соотношений. Отдельный раздел посвящен определяющим соотношениям для ротационной моды, в качестве которых предлагается линейное уравнение

1 Л = L Л, Н e     % e

где L - константа   пропорциональности,

µ _e

1/2

= (Xр:р ) ,

%e = (L/:/T) ; здесь нужно отметить некоторую непоследователь ность при введении константы L. С одной стороны, при подстановке интенсивностей в соотношение (29) эта величина сокращается, с другой стороны, в цитируемой работе эта величина «для определенности» принимается равной 1. Эффективные моментные напряжения и кри- визны-кручения полагаются связанными линейным соотношением й e = C % e ■

С использованием предлагаемой модели решены задачи исследования поведения моно- и бикристалла с ГЦК-решетками при осадке в условиях плоско-деформированного состояния. Расчеты проводились как с учетом моментных напряжений, так и без них; во втором случае проведено сопоставление с моделью Бишопа-Хилла; отмечается, что при уменьшении показателя скоростной чувствительности вязкопластической модели результаты приближаются к полученным по жесткопластической модели (Бишопа-Хилла). Показано, что учет ротационной моды и моментных напряжений существенно влияет на форму свободной поверхности образца (особенно вблизи контактной поверхности и поверхности раздела в бикристалле), на зависимость нагрузки от деформации.

В работах [3-5, 13] предлагается упруговязкопластическая физическая теория, построенная на несимметричных мерах напряженного и деформированного состояния, предназначенная для описания эволюции мезо- и микроструктуры моно- и поликристаллических материалов в процессах интенсивных пластических деформаций (ИПД), в том числе для описания формирования текстуры. Показано, что при использовании несимметричных мер напряженного и деформированного состояния в математической модели мезоуровня некоторые из проблемных вопросов физических теорий (неоднозначность в определении активных СС; внесение в основные соотношения теорий физически необоснованных величин; противоречия в уравнениях баланса при рассмотрении процессов, связанных с интенсивными ротациями кристаллической решетки) можно разрешить без введения дополнительных гипотез [3]. Предлагается общая структура двухуровневой (мезо- и макроуровни) математической модели для описания деформирования поликристаллического агрегата в процессах ИПД: задается схема деформирования на макроуровне, на мезоуровне (зерно, субзерно) принимается модифицированная гипотеза Фойгта для меры скорости деформации. На макроуровне используется симметричный закон Гука в скоростной релаксационной форме; скорость пластических деформаций определяется из модели мезоуровня по скоростям сдвигов по активным системам скольжения (СС), для поиска которых, в свою очередь, используется определяющее соотношение вязкого типа. Предполагается, что процессы деформирования являются квазистатическими и протекают при низких гомологических температурах. Рассматриваются несимметричные меры скорости деформации и напряжений на мезоуровне; в качестве меры скорости деформации предлагается использовать транспонированный градиент скорости перемещений £ = vV . Мера деформированного состояния на мезоуровне q определяется коротационным интегрированием соотношения qr = q - w • q + q • w = ^ = vV. В качестве спина на мезоуровне предлагается использовать спин решетки w, то есть тензор, ассоциированный с вектором мгновенной скорости вращения кристаллической решетки. В качестве меры напряженного состояния используется тензор напряжений Коши без дополнительного предположения о его симметрии. Показано, что кривая, соответствующая несимметричному случаю, всегда лежит ниже кривой, соответствующей симметричной теории.

Отдельно обсуждаются вопросы построения несимметричного закона упругости на мезоуровне. Из классического вывода закона упругости можно утверждать симметрию тензора 4-го ранга c , описывающего упругие свойства материала, по парам индексов, c ijkl = c klij . Утверждать симметрию c внутри пар индексов нельзя в силу несимметрии на мезоуровне мер напряженного и деформированного состояний. Показано, что для материала с кубической симметрией тензор упругих свойств c имеет 4 независимые ненулевые компоненты - С 1111 , c ₁₁₂₂, c ₁₂₁₂, c ₁₂₂₁; предлагается методика численной идентификации компонент c ₁₂₁₂, c ₁₂₂₁, полагающихся в классической теории совпадающими [4].

Предложен новый способ описания эволюции ориентаций решеток зерен как следствия несовместности пластических деформаций в соседних элементах ротации, а также несбалансированных усилий на границе элемента ротации вследствие несимметрии тензора напряжений Коши. Отдельно рассмотрены вопросы перехода от величин мезоуровня на макроуровень, в частности подходы к определению макроповорота [13].

Результаты моделирования, в том числе эволюция функции распределения ориентаций решеток зерен, для поликристалла при нагружениях, соответствующих осадке, стесненной осадке и равноканаль- ному угловому прессованию, удовлетворительно согласуются с известными теоретическими и экспериментальными результатами.

К направлению, связанному с понятием «геометрически необходимой дислокации» (ГНД, GND), относится работа [54]. Отмечается, что основанные на однородности деформирования (сдвигом) модели и связанные с ней однородности распределения дислокаций в системах скольжения оказываются недостаточно адекватными при описании поведения материала на более малых масштабах. Для описания локальных искажений (кривизн-кручений) кристаллической решетки требуется введение неоднородных дислокационных субструктур, которые авторы также относят к «геометрически необходимым дислокациям». В связи с этим приведенная в [57] модель модифицируется введением дополнительной внутренней переменной - тензора плотности ГНД и кинетического уравнения для него, определяющего скорость изменения тензора ГНД через градиент скорости сдвигов. Последнее при использовании предлагаемой модели совместно с конечно-элементным пакетом требует вычисления в каждой гауссовой точке интегрирования вычисления указанных градиентов, что существенно усложняет процедуру интегрирования, в связи с чем значительная часть работы посвящена описанию предлагаемого авторами эффективного алгоритма интегрирования. Разработанный алгоритм встроен в коммерческий конечно-элементный пакет MSC.Marc200x и использован для анализа деформирования простым сдвигом монокристаллического алюминиевого образца. Сопоставление результатов расчета (кривые сдвиговые напряжения - сдвиговые деформации, интенсивности деформаций на боковой поверхности образца, сдвиговая деформация - до 55 %) с полученными авторами экспериментальными данными показывает хорошее соответствие. Для анализа влияния масштабного фактора проведены расчеты для образцов с уменьшенной высотой (1/2 и 1/10 от исходного), показано, что с уменьшением высоты образца повышаются сдвиговые напряжения и существенно изменяются поля плотности дислокаций и разориентаций решетки.

В статье [56], являющейся развитием рассмотренных выше работ авторов, отмечается важность учета в моделях поликристаллов границ зерен, которые могут служить мощными препятствиями для мобильных дислокаций. Предполагается, что подвижные дислокации могут пересекать границу зерен, оставляя в ней дислокации ориентационного несо- ответствия (ДОН), параметры которых авторы предлагают определять из условия минимума энергии ДОН. Для моделирования влияния границ предлагается использовать, как и для внутренности зерен, вязкопластическую модель с дополнительной энергией активации, пропорциональной энергии образования ДОН. Для численной реализации модели также применяется конечно-элементный пакет MSC.Marc200x и специальные элементы для учета границ зерен.

Разработанная модель применена для анализа процесса деформирования бикристалла с ГЦК-решеткой (алюминий) для трех разориен-тировок (авторы называют их «малой», «средней» и «большой»). В проведенных экспериментах и численных расчетах (простой сдвиг до 50 %) показано, что по мере увеличения разориентировок возрастает неоднородность интенсивности деформаций в кристаллах, составляющих бикристалл, что обусловлено возрастающим сопротивлением движению дислокаций границы кристаллов. Сопоставление результатов экспериментально измеренных на боковой поверхности образца интенсивностей деформаций и ориентировок с данными расчетов показывает хорошее соответствие.

В статье [55] рассматривается модификация предложенной авторами модели [54, 56] для описания поведения моно- и поликристаллов с ОЦК-решеткой. В отличие от ГЦК-кристаллов, где барьер Пайерлса мал по сравнению с сопротивлением дислокаций леса движению мобильных дислокаций, для ОЦК-кристаллов, напротив, можно пренебречь напряжениями от леса дислокаций в сравнении с напряжением Пайерлса; в остальном модель не отличается от изложенной в цитируемых выше работах. Модифицированная модель использована для анализа деформирования бикристалла ниобия при выдавливании образца через прямоугольную матрицу. Результаты расчетов сопоставляются с данными проведенных авторами экспериментов. Отмечается, что лучшее соответствие достигается при использовании для ОЦК-решетки в качестве потенциально активных систем скольжения <111>, {110} и <111>, {112}.

Отдельную группу составляют модели, являющиеся, по сути, развитием теории скольжения Батдорфа-Будянского [1-2], которые представляется возможным назвать «квазифизическими». Остановимся на одной из последних работ [68], содержащей краткий обзор моделей данной группы.

В цитируемой работе предполагается, что механическое поведение поликристаллического материала с хорошей точностью может быть описано небольшим (от 5 до 10) числом структурных элементов (СЭ), называемых авторами «зернами» (следует подчеркнуть, что в общем случае СЭ не являются зернами в обычном смысле, каждый СЭ может описывать поведение конгломерата зерен). СЭ выбираются в форме куба (хотя форма особого значения не имеет), в котором назначаются 6 независимых «систем скольжения»; заметим, что к СС в монокристаллах в общем случае (если СЭ действительно не представляет собой зерно) эти «системы скольжения» никакого отношения не имеют. Как и в физических теориях упруговязкопластичности, пластические деформации полагаются изохорическими, реализующимися сдвигом по введенным «системам скольжения». Используется неизотропный закон упрочнения (деформационное и латентное упрочнения определяются отличающимися модулями упрочнения); кроме того, для «систем скольжения» СЭ учитывается кинематическое упрочнение.

Модель ориентирована на совместное использование с МКЭ с высокой степенью аппроксимации и применением численного интегрирования по конечным элементам. Каждой точке интегрирования «приписывается» один или несколько (с использованием процедуры осреднения) СЭ с определенной ориентацией; ориентации СЭ определяются в соответствии с полюсными фигурами материала исследуемой области. На уровне конечных элементов (макроуровень) в качестве ОС используется закон Гука в релаксационной скоростной форме; скорости пластической деформации определяются в каждой точке интегрирования из упомянутых выше вязкопластических соотношений для соответствующих (одного или нескольких) СЭ.

Предложенная модель использована для решения нескольких тестовых задач (растяжение и простой сдвиг образцов, растяжение тонкой пластины с круговым отверстием). Сопоставление результатов с экспериментальными данными и результатами, полученными с помощью классической теории течения и физической теории упруговязкопластичности (40 зерен на КЭ) показывает их хорошее соответствие. При этом время расчетов по предлагаемой модели сопоставимо (превосходит не более чем на порядок при использовании 7 СЭ на точку интегрирования) время решения по теории течения и в 10-15 раз меньше времени расчета по физической теории.

• 7.    Структурно-аналитическая теория

Значительный вклад в развитие физических теорий внесен работами В.А. Лихачева и В.Г. Малинина. Обобщающие результаты многолетней работы по созданию модели, названной авторами структурно-аналитической теорией прочности и пластичности, содержатся в монографии [6], где приведен также весьма обширный список публикаций авторов.

Анализируя состояние физических теорий пластичности, авторы отмечают, что основным концептуальным недостатком этих теорий являлась попытка описать процессы деформирования, основываясь на рассмотрении поведения самой малой части, которую можно выделить в материале (например, субзерно, фрагмент), неучет самоорганизованной многомасштаб-ности процессов неупругого деформирования и разрушения.

В основу теории авторами положены следующие положения:

• 1.    Для описания поведения материала используется двухуровневая модель (микро- и макроуровень), для каждого из уровней вводится представительный объем; в пределах представительного объема соответствующие параметры каждого из уровней полагаются однородными.

• 2.    Все микрообъемы взаимодействуют друг с другом через микронапряжения. При этом вводится дополнительное поле микронапряжений, разделенное на две составляющие - ориентированные и неориентированные микронапряжения. Поля ориентированных микронапряжений порождаются неоднородными неупругими макродеформациями и не исчезают при снятии внешней нагрузки (в макросмысле). Поля неориентированных микронапряжений обусловливаются многими причинами, к числу которых относятся: несовместности температурных деформаций микрообъемов, неоднородности упругих характеристик на микроуровне, неоднородностей магнитострикционных и электрострикционных микродеформаций, неоднородность неупругих микродеформаций.

• 3.    Процессы деформирования на микро- и макроуровнях связаны между собой через соответствующие поля напряжений и деформаций.

• 4.    Физические константы теории являются фундаментальными характеристиками материала и не зависят от способа их калибровки в макроэкспериментах (принцип локальной калибровочной инвариантности).

В качестве процедуры осреднения принимается ориентационное и статистическое осреднение (по некоторым параметрам).

Детально анализируются большинство из известных механизмов упругого и неупругого деформирования (температурные, магнитострикционные, электрострикционные, диффузионные, вязкие (деформации ползучести), сдвиговые (за счет скольжения дислокаций), деформации двойникования, деформации за счет мартенситных реакций. Для каждого из указанных механизмов записываются определяющие напряжения микроуровня, связывающие скорости микродеформаций со скоростями и полными эффективными микронапряжениями. Для тензора скорости микродеформаций принимается гипотеза об аддитивности скоростей микродеформаций по всем реализующимся механизмам.

Учитывая тот факт, что основными механизмами неупругого деформирования моно- и поликристаллических металлов являются кристаллографический сдвиг и двойникование, рассмотрение этих механизмов выделено в отдельную главу. Приведены соотношения конститутивной модели для описания пластического деформирования, деформаций ползучести (с разделением их на деформации ползучести, обусловленные возвратом, и деформации термоактивируемой ползучести). Приведены результаты численных расчетов для различных пропорциональных и сложных нагружений, отмечается их хорошее качественное соответствие экспериментальным данным. Значительная часть монографии посвящена анализу прочности и разрушения поликристаллов, а также рассмотрению деформирования материалов с мартенситным механизмом неупругого деформирования (в частности, материалов, обладающих эффектом памяти формы). Указанные вопросы выходят за рамки тематики предлагаемой работы; интересующийся читатель может найти сведения о моделях материалов, описывающих твердотельные фазовые переходы, и чрезвычайно обширные экспериментальные данные в справочнике [8].