Физическое моделирование динамики структурированных частиц

Развитие современной прикладной теории управления (СПТУ) целесообразно проводить в направлении абстрагирования от второстепенных физических свойств объекта управления и в то же время сосредоточить основное внимание на основополагающих свойствах исследуемого материала. Другими словами, в физической и математической модели объекта управления необходимо выделить основные, базовые физические факторы, которые определяют сущность исследуемого вещества, материала, явления [1].

В качестве объекта исследования (управления) будем рассматривать материал как твердое тело. Это может быть металл, каменистая порода и другое. Современные передовые технологии, связанные с деформацией твердого тела, всё чаще используют знания о более низких масштабных уровнях вещества, таких, как микро, мезо и нано. Очевидно, что изменение свойств целого (макроуровень) можно получить за счет изменений на более низких масштабных уровнях [2]. При этом энергетические затраты на деформацию твердого тела могут быть намного меньше по сравнению с аналогичными затратами, сделанными для получения такого результата на макроуровне. Следовательно, процессом деформации материала желательно управлять на более низком масштабном уровне, управлять его внутренними свойствами (элементами, структурой, процессом самоорганизации и др.) [3]. Целенаправленным изменением процесса самоорганизации сложных систем (технических, экономических, социальных) занимается синергетическая теория управления, одной из ключевых проблем которой является математическое моделирование нелинейных динамических систем [1]. 2

Для понимания процессов, происходящих в различных материалах при их деформации (упругой, пластической и разрушающей) после внешнего воздействия, необходимо провести исследование. Для этого требуется создать некоторый условный образ – модель. Построение физической, а затем и математической моделей является одной из узловых проблем при описании объекта управления в задачах СПТУ. В действительности, полу-

ченная модель должна наилучшим образом отражать реальные процессы, происходящие при деформации материала.

В настоящее время в мире существуют два основных подхода (две основные концепции), описывающих реальные процессы в материи – это концепции непрерывности [4] и дискретности [5, 6]. Однако развиваются эти направления далеко не равномерно. Это можно объяснить в том числе неоднородностью развития составляющих технического прогресса – постепенными успехами в фундаментальных науках и скачкообразными достижениями в технике, связанными с развитием инструментальных средств, аппаратнопрограммных информационных технологий и вычислительной техники.

Реальный окружающий нас мир – дискретный. Это доказано, как на микро масштабном уровне (атомы, молекулы и др.), так и на мегауровне (планеты галактики и др.). Феноменологический подход, заложенный в основу непрерывной концепции вещества в основном на макромасштабном уровне, идеализирует его реальную дискретную основу. Этот подход базируется на понятии материального континуума и соответствующей этому понятию гипотезе сплошности. При определенных ограничениях и упрощениях на этой основе развита теория «Механика сплошной среды», на базе которой созданы многие прикладные технические науки: обработка металлов давлением, движение жидкости и газа, волновые движения в твердых телах и жидкости и др. [4]

Цель данной работы: построение дискретной физической модели деформации материала (металла) и исследование механизма внутренней его реакции после внешнего воздействия в свете задач СПТУ.

Физическая модель динамики структурированных частиц

Известно, что деформация материала подразделяется на упругую и неупругую. Свойство неупругой деформации материала подразделяется на хрупкую и пластическую. При исследовании как хрупкой (разрушительной), так и неупругой (пластической) деформации континуальная механика вынуждена делать ряд ограничений и в этих условиях производить расчеты. Это существенно усложняет решение задач автоматического управления инструментом процесса деформации во время обработки металла (материала) давлением. Следовательно, идеализация дискретной системы сплошной средой, в частности в процессах управления, не всегда удовлетворительна.

Концепция дискретности в описании процессов деформации материала на первый взгляд более удовлетворительна, хотя имеет ряд сложностей и трудностей при физическом и математическом моделировании. Одним из наиболее перспективных подходов для решения совместных задач де- формации и управления можно считать метод динамики частиц, который с успехом развивается на нано- и микромасштабных уровнях вещества (метод молекулярной динамики). Исследование процесса управления технологией деформации материала методом молекулярной динамики довольно сложно и нецелесообразно из-за большого количества частиц, которые приводят к лишним вычислениям, что явно нежелательно в процессе управления в реальном времени.

Однако концепция дискретности удобна для описания процессов деформации материала, так как наилучшим образом отвечает реальности и, при некоторой адекватности, удовлетворяет быстродействию принятия решения автоматической системой [7].

В качестве физической модели будем рассматривать материал как целое (макромасштабный уровень) и как систему структурированных частиц, состоящую из частиц 1, 2, 3… n, имеющую внутренние U и внешние G, F, Y связи (рис. 1) [7]. Целостность системы сохраняется благодаря внешним связям в пространстве, времени и масштабе (триада) [8]. Однако мы ограничиваем целое полнотой системы и исследуем деформацию твердого тела при граничных и начальных условиях на определенном масштабном уровне.

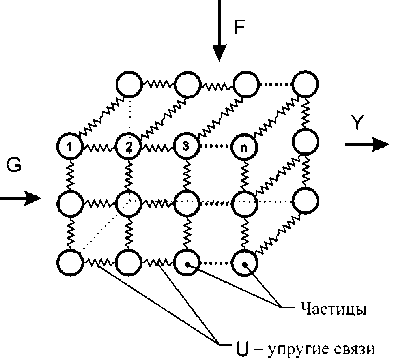
Рис. 1. Система структурированных частиц – Кластер

Опускаясь по масштабной лестнице ниже, имеем дело с мезоуровнем, который характеризует структурообразование целого. Для металла это может быть уровень зерен и их образований, для других материалов уровень гранул, одним словом, уровень частиц, которые формируют структуру вещества. Уровнем ниже расположены молекулы и атомы. Следует отметить, что каждый уровень имеет свое время активной «жизни» параметров частиц и их совокупности, свою скорость и частоту собственных колебаний. Для оценки свойств вещества вводятся базовые параметры: масса, расстояние и время [4].

Эта триада параметров и будет определять «жизненный цикл», «жизненную деятельность» частицы или группы частиц. В этом случае любую составляющую частицу в поле частиц целого можно рассматривать как осциллятор со своей массой, амплитудой, частотой, а при взаимодействии с другими частицами можно добавить и фазу. Выделение мезочастиц в форме зерен в металле, гранул в камне и т.д. удобно для исследования процессов деформации материала. При этом на вычисления будет потрачено времени намного меньше, чем при исследовании материала методом молекулярной динамики. Однако для оперативного управления процессом деформации этого тоже недостаточно. Рассматривая процесс разрушения структуры металла при гидроабразивной резке, было замечено, что металл распадается не только на зерна, но и на небольшие группы крепко связанных между собой зерен. Такое сильное объединение зерен в группы наблюдается и в обработке металлов давлением при прокатке полос толщиной примерно 0,5 мм и меньше. На поверхности листа образуются неровности, которые методом механики сплошных сред сложно как описать, так и управлять процессом пластической деформации. Дефекты поверхности прокатываемых полос, такие как «поперечная ребристость» и «поперечные теневые полосы» объясняются вибрацией прокатного оборудования в работах ученых Э.А. Гарбера, Г.Э. Аркулиса, В.М. Синицкого, и др. Однако объяснения причин появления названных дефектов у проката именно тонких полос нет.

Причины появления некоторых видов неровностей в тонких полосах проката, отрыва целых групп при гидродинамической резке можно объяснить наличием в материале (металле) отдельных групп структурированных частиц. Эти группы объединены какой-то закономерностью, например, уплотнением или разряжением структуры. Следовательно, при появлении уплотнений структуры в процессе прокатки может появиться утолщение. Во время гидродинамической резки такая структура может вызвать изменение некоторых механических свойств материала, что вызовет резонанс не частицы, а структурированной группы.

Таким образом, выдвинем предположение, удобное для описания механики тел (металл, материал, вода, воздух), состоящих из отдельных групп структурированных частиц, назовем их системой кластеров структурированных частиц (СКСЧ). Кластер (англ. cluster – группа, связка, скопление, гроздь) – группа объектов, выделенных в большую совокупность по определенному признаку. Например, из всего множества зерен металла выделим группы (совокупность) с уплотненной структурой, а другие группы имеют разряженную структуру зерен. У таких групп имеется характерный признак – плотность среды. Такой признак существенно сказывается на механических свойст- вах материала. Материал с таким характерным признаком называется неоднородным.

На рис. 2 представлена схема системы кластеров структурированных частиц. Эти кластеры имеют определенные размеры и некоторую самостоятельность. При внешнем воздействии G (прокатка, гидрорезка) на макротело, один из параметров которого, например толщина полосы при прокатке (расстояние) или площадь пятна гидрорезки, а следовательно, и уплотнения (масса), соизмерим с кластером структурированных частиц. Самостоятельные группы СКСЧ имеют свою массу, размеры и время активной «жизни» при внешнем воздействии. С помощью групп СКСЧ можно объяснить образование некоторых неровностей (шероховатостей) при прокате тонкого листа толщиной менее 0,5 мм.

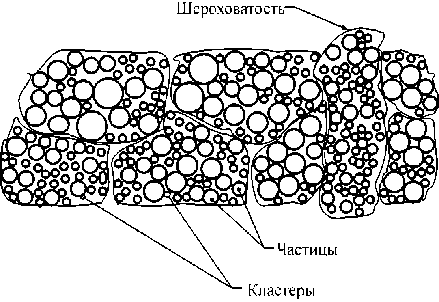
Рис. 2. Система кластеров структурированных частиц

Однако устранение этих неровностей обычным процессом прокатки не приведет к положительному результату, так как образование размеров кластеров частиц кроется в другом металлургическом процессе. Например, на прокатных станах ООО «Северсталь» при прокатке тонкого автолиста толщиной менее 0,5 мм до сих пор до конца не устранена причина неровностей. Для того чтобы ее устранить, необходимо определить основную причину, формирующую ключевую проблему образования разнотолщинности. Наличие СКСЧ и их размеров определяет наименьшую толщину листа при прокатке с удовлетворительным качеством. Исследуя процесс деформации материала целесообразно проанализировать и структуру воздействий.

Рассмотрим физику процесса разрушения материала при водоструйной резке (гидрорезка, гид-роабразивная резка), взяв за основу наличие в материале групп СКСЧ (рис. 2).

Физическая модельсверхзвуковой струи жидкости

Описание процесса гидрорезки и гидроабра-зивной резки материала привлекает ученых многих отраслей наук: физических, математических и технических. Эта передовая технология резки все больше и больше пользуется спросом при механической обработке материала. Достоинств много, но имеются и недостатки. Для того чтобы наилучшим образом оценить работу таких систем обработки материала, необходимо проанализировать физику, а затем и математику процесса деформации разрушения при гидрорезке и гидроабразив-ной резке.

Рассмотрим процесс деформации (разрушения) материала с физической точки зрения. На рис. 3 представлена схема водоструйной резки материала с использованием физической модели СКСЧ. Инструментом такой технологии является определенным образом сформированная струя воды (рис. 3), исходящая из специального сопла (имеющая катеноидальный профиль диаметром 0,08… 0.5 мм) со сверхзвуковой скоростью истечения до 1200 м/с. При этом давление воды в гидростате создается в пределах от 140 МПа до 420 МПа. На некоторых прогрессивных установках создается давление до 630 МПа. Возникает вопрос: почему вода даже без абразива режет камень, металл (лист до 3 мм толщиной), бумагу, пенопласт? Ответ на этот вопрос кроется в физике как структуры струи воды, так и процесса ее истечения, а также в структуре обрабатываемого ей материала.

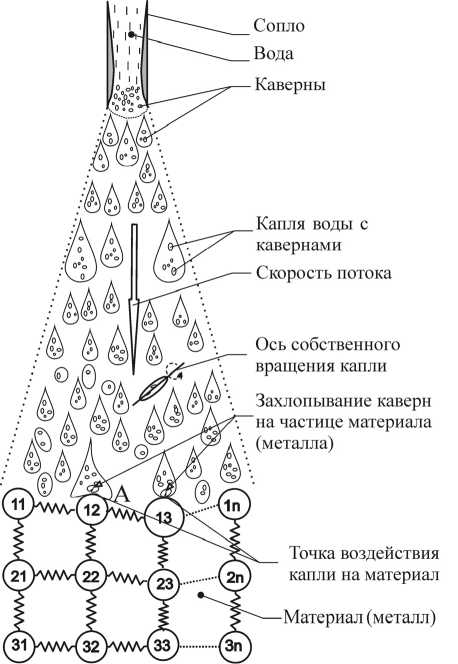
Рис. 3. Кинематическая схема водоструйной резки

Рассмотрим физику процесса гидрорезки материала более подробно. Вода для гидроабразивной резки предварительно проходит высокую очистку от солей и примесей. В установке (гидростате) создается давление, которое достигает 400 МПа и более. При выходе воды из сопла образуется струя. Наружное давление вокруг сопла – 0,1 МПа.

Струя воды, выходя из сопла, попадает в переменное поле давления, т. е. из высокого давления в низкое. При этом давление в воде падает и становится ниже некоторого критического P _кр, что является причиной появления кавитационных пузырьков – каверн, которые образуются в расширяющей части катеноидального профиля (рис. 3).

В начальной стадии струи, на выходе из критического сечения катеноидального сопла, происходит интенсивная парогазовая кавитация [9, 10]. Вода, попадая в свободное пространство (освобождаясь от стенок сопла), имеет градиент давления и, практически, происходит перераспределение энергии. Потенциальная энергия, заложенная в воду гидростатом, из-за перепада давления переходит в кинетическую энергию струи и в давление внутри пузырька (каверны) газа или пара. Таким образом, вода, вытекая из сопла, приобретает высокую скорость и имеет кавитационные пузырьки, внутри которых формируется очень высокое давление.

Двухфазный поток жидкости после катенои-дального сечения (вода и кавитационные пузырьки) на срезе сопла и далее в свободном состоянии образует две отдельные среды: капельную и парогазовую.

Рассмотрим капельную. Сплошной водяной поток в свободном состоянии разрушается и благодаря наличию у жидкости независимой поверхности натяжения, которая, замкнувшись, создает каплю. Сама жидкость при различной скорости свободного движения ведет себя по-разному. Например, вода при малых скоростях (намного меньше скорости звука) обладает эластичностью, гибкостью, т. е. обладает свойствами, характерными для жидкости, а при больших скоростях становиться прочной и порой обладает свойством твердого тела. При этом размеры капли с увеличением скорости ее движения существенно уменьшаются.

Форма капли воды в зависимости от скорости ее движения имеет различный вид. Под действием сил поверхностного натяжения капля стремится сохранить сферическую форму. Двигаясь в свободном падении, когда отсутствуют внешние боковые силы, капля приобретает форму сфероида – вытянутого эллипсоида вращения. При появлении неравномерных боковых внешних сил (силы давления и трения) капля воды начинает вращение, и форма ее может иметь как вытянутый, так и сплющенный эллипсоид вращения. Эти силы и еще кавитация снижают устойчивость капли и большая капля разбивается на более мелкие.

Рассмотрим движение капли воды, двигающейся со сверхзвуковой скоростью (примерно 1000 м/с). Как было отмечено ранее при выходе из катеноидного сопла струя жидкости (вода), за счет кавитации, образует капли и парогазовую оболочку (рис. 3). Капля, двигаясь с большой скоростью в парогазовой среде, частично испаряется и дробится на более мелкие капли за счет трения о воздух, скорости движения и кавитационных каверн внутри нее.

Кавитация на выходе из катеноидального сечения, отрыв и формирование капли воды на срезе сопла, а также соударение с другими каплями создают неравномерность действия на нее сил, которые в свою очередь придают рассматриваемой капле вращение. Большая скорость, маленький объем и высокое внутреннее давление воды (благодаря поверхностному натяжению) позволяют рассматривать форму капли как сферическую. При этом условный диаметр такой капли может составлять десятки и сотни микрон.

Траектория движения капли в парогазовой среде со сверхзвуковой скоростью довольно сложная. Под действием внешних сил (инерции, трения, центробежных и центростремительных) капля совершает собственное вращение относительно своей оси, которая может быть вертикальной, горизонтальной либо под углом по отношению направления скорости движения потока (рис. 3). От положения собственной оси вращения в пространстве будет зависеть окончательная траектория движения капли: поступательная или вращательная относительно какой-нибудь другой оси, кроме собственной. Следовательно, имеет место сложное движение капли. В результате чего капли могут изменять свое направление и рассеиваться.

Таким образом, рассматривая модель сверхзвуковой струи жидкости, делаем вывод: большая скорость движения капель в струе и ряд приложенных к ним сил увеличивают площадь рассеивания капель, что существенно снижает эффективность работы гидрорезки материала.

Механизм разрушения материала капельной жидкостью

Предлагается новый подход описания физического процесса разрушения материала гидравлической струей (капельной жидкостью). Он основывается на методе динамики частиц, составляющих гидравлическую струю (капли жидкости), и частиц, из которых состоит материал, подвергающийся разрушению.

Рассмотрим более подробно, как капля воды воздействует и разрушает материал. Сосредоточим внимание на капле, движущейся со сверхзвуковой скоростью и достигающей поверхности материала (металла). Скорость движения капли в этом случае будет составлять примерно от 600 до 1000 м/с, а ее диаметр – от 10 мкм до 500 мкм.

Небольшой размер и большая скорость движения капли позволяют сделать следующие допущения и условия: 1) движущуюся каплю в момент ее контакта с разрушаемым материалом, будем рассматривать как твердое тело; 2) размер капли соизмерим с мезочастицами (зерна металла, гранулы камня и т.д.) или с размером кластера структурированных частиц материала; 3) в капле имеются кавитационные каверны; 4) на разрушающий материал действует непрерывный капельный поток; 5) капли в капельном потоке имеют различную массу.

Будем рассматривать механизм разрушения материала на примере с металлом. Металл состоит из зерен, которые, как уже отмечалось, имеют различную массу и размер. Каждое зерно жестко связанно с соседними зернами и, следовательно, имеет определенную собственную частоту. Как предполагалось ранее, совокупность зерен образует кластер структурированных частиц. В этом случае металл, состоящий из структурированных частиц и кластеров, можно рассматривать как систему осцилляторов с широким диапазоном частот.

Капля, движущаяся с большой скоростью, сталкиваясь с металлом, производит удар, который приходится на зерно или на кластер структурированных частиц. Зерно металла от такого воздействия начинает совершать колебательные движения на своей собственной частоте. Так как капельный поток не снижается, а капли имеют различную массу и скорость, то капли воздействуют с различной частотой, в том числе и с частотой, совпадающей с осциллятором-зерном (см. рис. 3). Если частота внешнего воздействия совпала с собственной частотой осциллятора, то имеет место явление резонанса.

Частица (зерно, кластер) в результате резонанса отрывается от соседних и увлекается капельным потоком вниз. Эти частицы, в свою очередь, имея массу больше чем у капель воды, приобретают скорость и становятся тоже инструментом, который воздействует на другие частицы. Происходит лавинное разрушение.

Следует отметить еще одно физическое явление, которое происходит при контакте капельки воды с частицей металла (зерно, кластер). Как было отмечено ранее, в процессе формирования капли воды на срезе сопла в ней образовывались и сохранялись кавитационные каверны. При контакте капли и частицы металла каверны захлопываются и при этом выделяется большая энергия, которая направлена на частицу. Такое дополнительное воздействие на частицу увеличивает процесс резонансного разрушения.

Заключение

Представленная физическая модель системы кластеров структурированных частиц существенно упрощает как описание, так и процесс пластической и разрушительной деформации материала. Эта модель дает возможность не только рассматривать дефекты, возникшие при прокатке тонкого листа (толщиной не более 0,5 мм), но и отыскивать пути их устранения. Причина неровностей проката кроется не в резонансе части оборудования прокатной клети, а в физической структуре обрабатываемого давлением металла. В том случае, если размер кластера структурированных частиц соизмерим с толщиной прокатного листа, то на поверхности появятся неровности, что существенно снижает качество проката. Если уменьшить силу взаимодействия между частицами металла, определяющую структурную связь, то можно добиться улучшения качества поверхности и проката в целом.

С помощью физической модели СКСЧ легко объясняется гидрорезка и гидроабразивная резка материала. В настоящей работе СКСЧ рассматривается как система осцилляторов. Струйный поток парогазовой среды с каплями воды движется со сверхзвуковой скоростью и воздействует на СКСЧ материала. В результате энергия капли, абразива и кавитационной корпускулы, воздействуя на частицу или кластер материала в широком частотном диапазоне, вызывает в последнем резонанс. Последствия резонанса – лавинное разрушение материала. При этом продукты разрушения материала в последующем так же, как и капля, являются инструментом гидроабразивной резки.