Физико-химические основы технологического процесса подземное выщелачивание

Технологические процессы подземного выщелачивания по своей структуре являются сложными техническими многосвязными системами, охватывающими несколько подсистем (пласт-скважина - насосные станции - концентрации реагентов и т.д.). Все эти подсистемы взаимосвязаны, и нарушение технологического режима хотя бы одной из подсистем приводит к остановке всего цикла работы системы в целом. Поэтому в настоящее время большое внимание уделяется прогрессивным методам разработки многокомпонентных систем, одним из которых является метод подземного выщелачивания (ПВ). Метод ПВ по сравнению с другими методами наиболее экономичный и безвредный, а его использование не приводит к нарушению окружающей среды.

Сложность процесса, протекающего в реальных подземных условиях, обусловливает необходимость разработки математических моделей и программного обеспечения для изучения всего цикла технологического процесса ПВ в реальных условиях и принятия решений в соответствии с целью управления. Основная цель создания модели – характеристика и прогнозирование некоторых объектов и технологических процессов. Модели, основанные на математической интерпретации проблемы, помогают в поиске необходимой информации для принятия решений с помощью определенных алгоритмов. Таким образом, разработка моделей для решения проблем анализа и принятия решений в управлении технологическими процессами подземного выщелачивания при добыче полезных ископаемых в рудных месторождениях, а также создание соответствующих вычислительных алгоритмов и программного обеспечения являются актуальными на сегодняшний день.

Растворение полезного компонента в недрах земли и последующее движение образовавшихся соединений происходят в основном в соответствии с гидродинамическими законами, законами массопереноса и химической кинетики. Сложность процесса, протекающего в реальных подземных условиях, обусловливает необходимость разработки математических моделей и программного обеспечения для изучения всего цикла технологического процесса ПВ в реальных условиях и принятия решений в соответствии с целью управления. Основная цель создания модели – характеристика и прогнозирование некоторых объектов и технологических процессов. Модели, основанные на математической интерпретации проблемы, помогают в поиске необходимой информации для принятия решений с помощью определенных алгоритмов. Математическая модель управления для принятия решений при анализе технологического процесса ПВ предлагается в следующем уравнении, отображающем характер изменения фильтрационного потока:

д ( kh дH У

--- дx ^ м дx )

д( kh дH У +

дУ I М дУ J

N                     д H

+ V^8(x - x, y - У,) Qi(t) = mhp—

7 = 1                                д t

в области G = { ( x , y , t)/ a <  x <  b , c <  y <  d, 0 <  t <  T_k } , удовлетворяющей граничным

, д H

( a —— + (1 - a )H ) / Г = ^ ( x, y ) и начальным H ( x , y ,0) = H ₀ ( x , y ) условиям. д n

После решения задачи (1) и определения напора Н находится скорость фильтрации по закону Дарси: vx

^{— k} i

дH дx ’

v y

^{— k} 2

д H дy '

С целью определения концентрации полезного компонента в пласте рассматривается уравнение конвективной диффузии:

Af D де Y AfD дС^дУС)-SM-YC - C_)= m дС, дx V  дx J  дy у  дy J    дx      дy                 дt

— = Y(C)f (C, N, L, Г), N(x, y,0) = Nо (x, y) дt в области G с начальным С(x, y,0) = С0 и граничным дС

( a    + (1 - a )C )

д n

= y/( x , y , t ) , а также внутренними

Г

= с ,

^{( x} , y ) = ^{( x} i , y i )          i

д С

д n

^{( x} , y ) = ^{( x} j , y j )

условиями.

Главная задача состоит в обеспечении целесообразных действий с помощью управления процессом ПВ и выборе параметров, гарантирующих осуществление следующих основных целей: минимизация притока реагента через рудоносные границы пласта; обеспечение равномерного гидродинамического выщелачивания; максимизация значений концентрации полезного компонента; оптимальное расположение скважин.

Эти цели реализуются путём минимизации целевой функции R выбором критерия оптимизации (U), т.е. решением задачи

T N t

R ( U ) = £ [ C ( X , U ) - C ib ( X , U )]² dt , R * = min R ( U ), R ( U *) <  s , U ₀ <  U <  U n ,

U∈Ω о i=1

ⁿ = ^{ Y , q o , q K ^}

Здесь C (X, U ) – решение задачи (1)-(2) в точке (x,y) в заданный момент времени t, С_b(X, U ) – требуемое оптимальное значение полезной компоненты,

ε – заданная точность, U – вектор с компонентами, γ – концентрация кислоты в закачиваемом растворе, q0, qk – дебиты скважин, ν – скорость фильтрации и др.

Вводятся следующие критерии управления для решения этой задачи.

Допускается,

что уравнение фильтрационного потока описывается уравнением d 2 H d 2 H  1 dH

+      =       + f (x, У, t) , dx2   dy    x dt удовлетворяющим

начальному     H ^{( x} , У , t ) _t = ₀ = H o ^{( x} , У )

и граничному

d H ( x , y , t )

∂ n

µ ^N

= 0 условиям. Здесь, f(x,y,t) = ^^qi(t)^(x x,y yi).

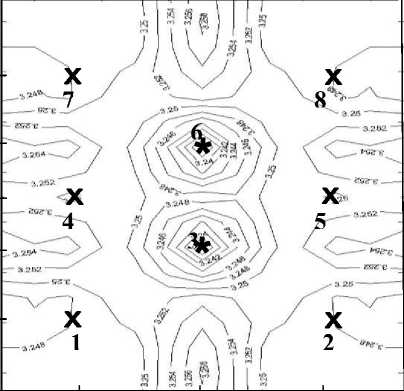
По результатам вычислений ниже показано изолинии напора :

^e.

60        80

Итак, для принятия необходимых решений в целях управления технологическим процессом ПВ решаются следующие задачи: системное исследование объекта ПВ, обработка данных, математическое моделирование, создание вычислительных алгоритмов, объектно-ориентированное программирование.

А также получение результатов на вычислительной машине, системный анализ полученных результатов для принятия решений в управлении процессом.

Из-за сложности процесса ПВ выбор параметров происходит не одновременно, а по отдельности. Гидродинамические параметры выбираются с использованием гидродинамической модели для процесса ПВ. В качестве экспериментальных значений используются динамические величины, примененные в предыдущей разработке. После этого выбираются кинетические параметры. В этом случае выходящими параметрами или последней целью является максимизация значений концентрации откачной скважины.