Физико-математическое моделирование эффективной площади отражения местности с учетом различных типов подстилающих поверхностей

В связи с ростом интереса, к освоению Арктики, оптимизации природных ресурсов, оценки качества, транспортных магистралей, введению разработок РЛС комплексов возникает необходимость усовершенствования средств мониторинга, ледовых покрытий, обширных лесных массивов, состояний искусственных покрытий. К настоящему времени накоплен богатый опыт зондирования и разработаны эффективные методы обработки рассеянных сигналов с целью опознания объекта [1-6].

В настоящей работе использованы некоторые из этих методов в целях создания программного комплекса, моделирующего сложную подстилающую поверхность.

Известно, что моделирование ЭПО сопряженно с большими трудностями ввиду непредсказуемости рельефа подстилающей поверхности, а также физико-химических свойств материала. облучаемого объекта. В этой ситуации моделирование ЭПО отраженного сигнала, возможно только статистически или полуэмпирически.

«Московский физико-технический институт (государственный университет)», 2018

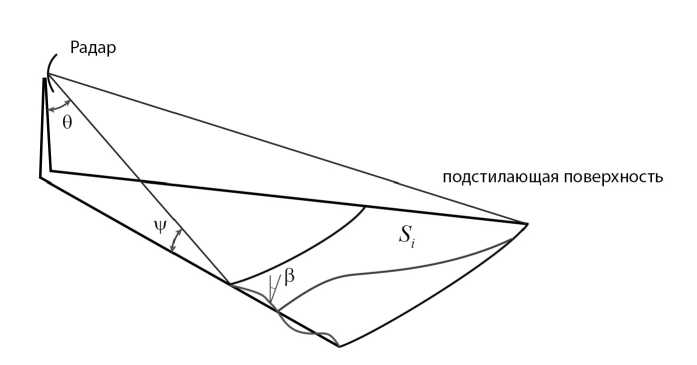
Рис. 1. Схема облучения подстилающей поверхности радаром

• 2.    Моделирование ЭПО водной и ледовой поверхности

Статистическое определение ЭПО шероховатой подстилающей поверхности имеет вид [1]:

/ pS ps* \ арq = 4^R2         ,

Р ^{4         0} Е^г_дЕ^г д * ,

где р и q - индексы поляризации, Е ^ - падающее электромагнитное поле, Е р - отраженное поле, Ro - расстояние от излучателя (приемника) до облучаемой цели, скобки означают осреднение по поверхности. Ясно, что в зависимости от величины амплитуды неровностей по отношению к длине волны могут быть использованы различные подходы.

Ниже рассмотрены два метода моделирования ЭПО воды и льда [1, 2]: приближение Кирхгофа и метод малых возмущений. Первый из них годится для шероховатых поверхностей большой амплитуды, второй - соответственно для шероховатой поверхности малой амплитуды.

ЭПО отраженного сигнала по Кирхгофу имеет вид

_ лк² ||^Q||²         2

^apq =      4     • Epq I • P^{rob( q} x ^/q z . ^q y ^{/ q} z ^).

q z

Входящие сюда величины определены в работе [1, 2]; сомножитель Prob(—q_x/q_z, — q_y/q_z ) - двумерная функция вероятности шероховатой поверхности, в частном случае волнистой поверхности воды.

Скорость ветра Пщ измеряется на высоте 10 м над уровнем моря. В этом случае

Prob«. ц) = ^(^ ^ ) 2ла с о_и

exp(-

(^/^ с )² + (рҚ )²

) .

Приведенные здесь величины имеют следующий вид:

а с = V0.003 + 0.00192П10. Q u = V0.00316Пщ.

G4 (фц) = 1 — 0.5А21 (е2 — 1)ц — 1/6Аоз(^3 — 3ц) + 1/24А40 (£4 — 6^2 + 3)+ +1/4А22«2 — 1)(ц2 — 1) + 1/24А04(ц4 — 6ц2 + 3),

А21 = 0.01 — 0.0086П10. А03 = 0.04 — 0.033Пщ. А40 = 0.4.

А₂₂ = 0.12. А₀₄ = 0.23.

Данная модель применима для скоростей ветра в диапазоне от 1 до 15 м/с.

Далее рассмотрим метод малых возмущений. В этом случае ЭПО сигнала имеет вид apq = 8к3 |cos Өі cos Ө®apq|2 S(кх. ку).

Входящие в это выражение величины определены в [1, 2]. S(k_x, к у ) - спектр высот морских возмущений. Приведем вкратце описание этого спектра, подробно рассмотренного в работе [3].

Выражение для S (к_х, к у ) имеет вид в полярных координатах (к_ж = к cosy, к у = к sin у.):

S(k, y_s) = к"3(В₁ + B_h)(1 + А(к) cos2y_s).

Здесь В/(к) = 0.003П⁰'⁵⁵/(£)Ғ_р(к), с_р « 1.17U10 - фазовая скорость на спектральном пике, с(к) = д/к (д=9.81) - фазовая скорость волны.

Далее, Ғ р (к) = ехр(—4(кр/к)²)7р(к)ехр(-^L (^к/к р — 1)), П « Uio/cp' J р (k) = 7 ^г(к\ 7 = 1.7 + 6ln(Q), Г(к) = ехр(—(^ к/к_р — 1)2/2ст²), ст = 0.08(1 + 4П^-3), к_р = gQ²/U2o -волновое число на спектральном пике.

Функция В^(к) = 0.5а_т^)Ғ^(к). Здесь «_т = 0.014и*/с_т, и* ^ 0.4м/с - скорость турбулентных пульсаций у поверхности моря, с_т ~ 0.23м/с - фазовая скорость на спектральном минимуме: Ғ_т(к) = ехр(—0.25(к/к_т — 1)2), к_т ~ 378м^-1 - волновое число на спектральном минимуме.

А(к) = th[«o + ар(с(к)/ср)²'⁵ + ат(ст/с(к))²'⁵], «о = (ln 2)/4, «р = 4.

Видно, что данный спектр сильно зависит от волнового числа к падающей волны, а также от скорости ветра Uio, как и в модели Кирхгофа.

Расчет ЭПО ледовой поверхности проводился согласно однослойной модели ледового пласта [4]. Общие выражения для двух поляризаций электромагнитной волны имеют вид

.31     2         2 (^)2             1

СТ ҺҺ = ^8к I ^cos Ө з «мД ^ (1 + (2к sin 0/)2)1.5 ’

^CTvv = ^{8к 1 cos Ө}3«vv ¹        73          . т\₂\1 5 ^.

4л (1 + (2кsin ӨІ)²)¹ . ⁵

Здесь һ - среднеквадратичная высота неровностей ледовой поверхности, I - корреляционная длина неровностей. Коэффициенты а_рч - такие же, как и в выражении (1).

• 3.    Моделирование ЭПО асфальтовых и бетонных дорог

Расчет ЭПО асфальтовых и бетонных дорог можно провести при помощи метода, аналогичного методу малых возмущений, в силу того что размеры характерных шероховатостей этих поверхностей можно считать много меньшими длины облучающей волны для сантиметровых диапазонов. Выражение для ЭПО сигнала в этом случае имеет вид [5]:

sb=78 ,T <г2)к4/0

∞

р(г) Jo(2kr cos 0)rdr, где Ө - угол падения, отсчитываемый от горизонтали, /г2/ - среднеквадратичная высота неровное той. р(т) - автокорреляционная функция неровностей на поверхности. Jo (ж) -функция Бесселя нулевого порядка. Коэффициенты Френеля при вертикальной и горизонтальной поляризации соотвественно имеют вид

T = г__________ ^Е1 ^{+ гЕ}2 ^{— 1} __________]2

^һ    {sin Ө + (Е1 + ге₂ — cos² Ө)¹/² }² ’

T v = [

(Е1 + іе ₂ — 1)[(Е1 + іе₂ )(1 + cos² Ө) — cos² Ө] {(Е1 + %е ₂ ) sin Ө + (Е1 + гЕ₂ — cos² Ө)¹/²}²

]2,

где Е1 + гЕ2 - комплексная диэлектрическая проницаемость.

Выражение автокорреляционной функции и диэлектрической проницаемости для бетона имеют вид

р(г) = exp(—7r)r, см, г² = 2, 6 * 10 ⁴ см 2, Е1 + ze₂ та 6, 5 + г1.5;

для асфалвта:

р(г) = [1 + 20r²] ^3/2, см, г² = 1, 6 * 10 ³ см², Е1 + ІЕ2 та 4.3 + г0.1.

• 4.    Моделирование ЭПО сложной местности

Таким образом, выше были рассмотрены аналитические методы расчета слабошероховатых поверхностей. Однако в случае отражения от сложного релвефа, например местности, покрытой лесом, трудно построить аналитическую модель. В связи с этим предлагается полуэмпирический метод, так называемый «постоянной у».

Выражение ЭПО некоторой местности (без учета поляризации) в данном подходе имеет вид [6]:

ст0 = сҒД = у sin Д ҒД, где Д - угол падения, отсчитываемый от горизонтали, у - параметр, описывающий отражающую способность покрова (определяется эмпирически); Ғд (pattern propagation factor) - поправка, вводимая для принимаемого радаром сигнала вследствие присутствия подстилающей поверхности. Для небольших углов Д можно записать:

^{Д 4}лст_һ

Ғ та Д ■

Ri

R ,

где Д_с - критический угол падения, щ - среднеквадратичная высота неровностей на поверхности. Для углов, больших Д_с, полагают Ғ_с та 1.

Таблица!

Параметры подстилающей поверхности

Тип поверхности	Коэффициент у (Дб)	щ, ср. кв. высота	Ср. кв. Скат 5»
Горы	-5	100	0,1
Городская местность	-5	10	0,1
Лестные холмы	-10	10	0,05
Горные холмы	-12	10	0,05
Пустынная местность	-15	3	0,03
Равнины	-20	1	0,02
Плоская местность	-25	0,3	0,01.

При стремлении Д ^ л/2 ЭПО описывают с помощью выражения «квазизеркального» отражения [6]:

. =  Р2 е^52 ] ^ 52 + 0.36Ө@     52 + 0.36Ө@ где 5 ~ угол падения, отсчитываемый от вертикали, 5» ~ среднеквадратичный угол ската неровностей на поверхности. Ө@ - угловая ширина сигнала, посылаемая радаром, р = рор8ру - коэффициент отражения, определяемый через коэффициент Френеля р», эффективный коэффициент отражения от шероховатой поверхности р8 и коэффициент поглощения в присутствии растительности ру.

Формулы для расчета этих коэффициентов для вертикальной и горизонтальной поляризации соотвественно имеют вид [6]:

^ sin Д — Е_с — cos² Д sin Д + Е_с — cos² Д

Е_с sin ф —   Е_с — cos² ф

Е_с sin ф + л/Е_с — cos² ф

Здесь Е_с = Е_г — г60Асу - комплексная диэлектрическая проницаемость.

p_s = exp[—0.5(

4ттщ. А

sin ф)2],

Т а б л и ц а 2

Диэлектрическая и магнитная проницаемости различных типов материалов подстилающих поверхностей

Материал	Е г	се
Влажна почва	25	0,02
Почва	15	0,005
Сухая почва	3	0,001
Снег, лед	3	0,001
Пресная вода (А = 1m)	81	0,7
Пресная вода (А = 0, 03ттг)	65	15
Соленая вода (А = 1m.)	75	5
Соленая вода (А = 0, 03ттг)	60	15

• — 5 Дб, тонкая трава,

  Р у ~

  
  

• —    15 Дб, низкие кустарники,

• — 25 Дб, густые деревья.

• 5.    Основные результаты моделирования

Сшивка функций т⁰ и с ® проводится из условия и0(фо) = т®(фо).

Рассмотренные выше математические модели легли в основу программного комплекса по моделированию отраженного радиосигнала от земной поверхности. Пример распределения ЭПО отраженного сигнала по углу Ө (см. рис. 1), отсчитываемого от вертикали, представлен на рис. 2, 3 для водной и ледовой поверхностей.

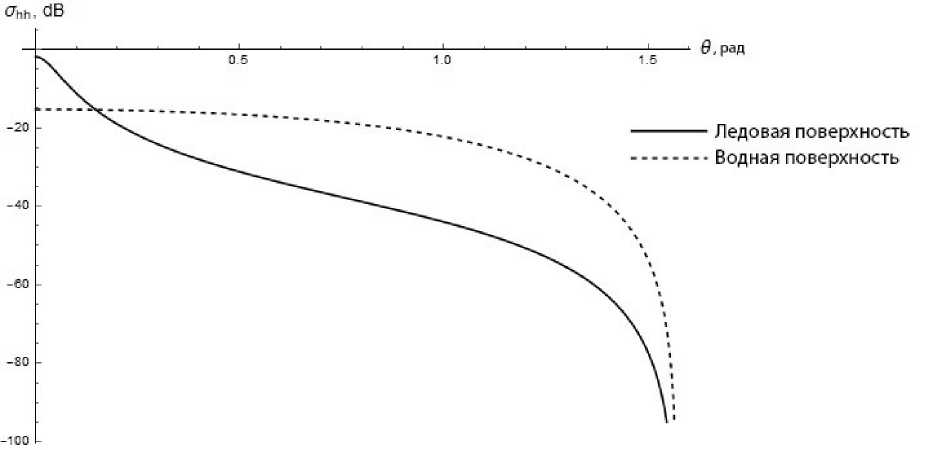
Рис. 2. ЭПО водной поверхности при U 10 = 10 м/с, А = 1м/с

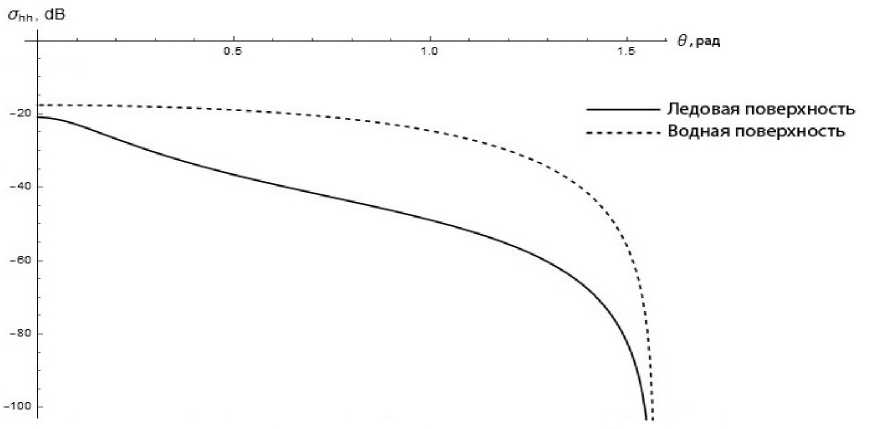
Рис. 3. ЭПО водной поверхности при U 10 = 10 м/с, А = 3 м/с

Видно, что при увеличении угла Ө происходит монотонное падение ЭПО отраженного сигнала. Аналогичная картина наблюдается и в распределении для других типов поверхностей.

В разработанном программном комплексе задается высота установки радара над уровнем моря и облучаемый сектор (рис. 1), в который, вообще говоря, входят различные виды поверхностей (например, леса и водоемы). Для определения ЭПО отраженного сигнала от смешанного типа поверхности применяется следующее соотношение:

= EaS а    Е, S, ’ где а, - ЭПО данного тина поверхности, S, - его площадь. Таким образом удается определить приближенное ЭПО для данного облучаемого сектора.

• 6.    Заключение

На основе известных аналитических и полуэмпирических моделей ЭПО отраженного сигнала создан программный комплекс моделирования ЭПО местности. Приведены иллюстрации расчетов для некоторых типов поверхности. Разработанный комплекс имеет практический интерес для виртуального испытания проектируемых РЛС установок.

Статья подготовлена по государственному заданию № 8.12870.2018/12.1.