Физико-математическое моделирование особенностей формирования угловых швов мостовых металлоконструкций при дуговой сварке под флюсом

УДК 621.791.75:004.942                                   

Введение . Традиционные методы строительства мостов предусматривают укрупненную сборку объемных сварных металлоконструкций на месте строительства [1]. Поэтому на самом объекте сварочные работы проводятся по минимуму. Они выполняются, в основном, на заводах мостовых металлических конструкций [2], и бо_́льшая их часть связана со сваркой протяженных швов. Из них на угловые приходится от 40 % до 70 %. Угловые швы при малой толщине свариваются без разделки кромок. При толщинах до 50 мм применяются асимметричная и симметричная разделки с углом раскрытия 45–60°. Оптимальны угловые швы с плоской поверхностью в поперечном сечении и плавными переходами к основному металлу по зонам сплавления без наплывов и подрезов, газовых полостей и шлаковых включений. Помимо этого сварные соединения должны обладать высокой пластичностью и ударной вязкостью при низких температурах. Недопустимы дефекты формирования швов. Бездефектное воспроизведение максимально возможного катета при сварке угловых швов является основным резервом повышения производительности [3].

Для минимизации дефектов и повышения производительности процессов сварки мостовых металлоконструкций угловые швы с максимально возможным размером катета желательно сваривать в один проход. Поэтому актуальной задачей является увеличение катета, свариваемого за один проход [4]. Этого можно достичь:

— оптимизацией параметров процессов сварки,

— использованием новых источников нагрева,

— сокращением вспомогательного времени,

— повышением легкоплавкости электродной проволоки.

В первую очередь следует рассмотреть возможность бездефектного воспроизведения в заводских условиях максимально возможного катета при использовании традиционной технологии сварки под флюсом плавящимся электродом.

Цель настоящей работы — изучение возможностей увеличения производительности процесса дуговой сварки угловых швов с учетом особенностей их формирования.

Материалы и методы. Как отмечается в [5], помимо общеизвестных параметров режима сварки (ток дуги, скорость сварки) на производительность процесса сварки под флюсом влияют напряжение дуги и диаметр электродной проволоки. Пространственное положение при сварке и позиционирование электрода в разделке также существенно влияют на формирование угловых швов [6]. Рассмотреть влияние всей совокупности перечисленных факторов на производительность процесса сварки и качество угловых швов без использования современных методов исследования — крайне трудоемкая задача.

Для существенного сокращения объема экспериментальных исследований сварки угловых швов применяют физико-математическое моделирование напряжений и особенностей формообразования и провара [7–9]. Рассмотрим последовательность компьютерного моделирования особенностей формирования угловых швов — от создания модели до ее визуализации. Основное отличие способа дуговой сварки под флюсом от дуговой сварки в защитном газе состоит в том, что дуга горит в парогазовой полости, возникающей из-за плавления и испарения флюса. Вторая важная особенность: физические явления, определяющие формирование сварочной ванны и шва, протекают в разных средах [9]. Это следует учесть в физикоматематической модели формирования шва при сварке под флюсом.

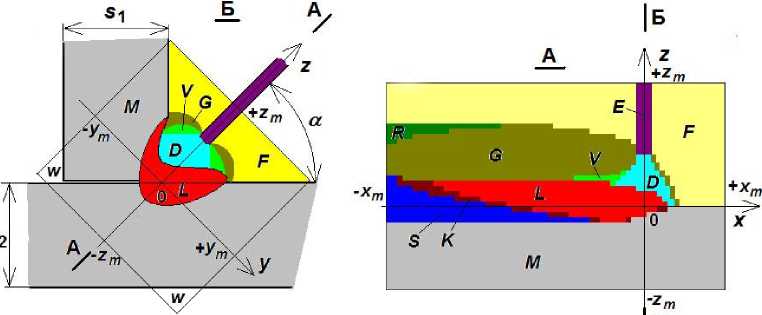
Координаты пространства моделирования. При моделировании обозначают пространство, в котором происходит сварка угловых швов, и геометрические размеры качественных швов. На рис. 1 а выделена область пространства, охватывающая свариваемые кромки и зоны горения дуги, плавления флюса и металла, а на рис. 1 б — геометрические размеры угловых швов, по которым можно оценить качество их формирования в соответствии с рекомендациями [5].

Б

а )

б )

Рис. 1. Строение пространства моделирования процесса сварки ( а ) и геометрические размеры угловых швов ( б ), определяющие качество их формирования

Машиностроение и машиноведение

Пространство моделирования включает зоны: M — исходный металл, E — электрод, D — сварочная дуга, F — сыпучий флюс, V — пар флюса, G — расплавленный флюс, R — затвердевший флюс, L — жидкий металл, K — твердожидкий металл, S — металл шва, W — воздух. Внутренние межзонные поверхности обозначены как пересечения множеств точек, принадлежащих соответствующим зонам. Например, поверхность сварочной ванны ZL (x, y) обозначена Ln(DиVaG). Она отделяет сварочную ванну L от сварочной дуги D, парообразного V и жидкого G флюса. Размеры зон V, G, L, K и расположение поверхностей раздела между ними неизвестны. Их необходимо определить при моделировании. Эти показатели зависят от результатов решения системы уравнений, описывающих физические явления сварки под флюсом. Такую задачу удобнее решать в неподвижной Декартовой системе координат, в которой металл свариваемого стыка неподвижен, а электрод и дуга перемещаются со скоростью сварки vw по направлению координаты x. Соответственно, координаты оси электрода xj и yj определяются:

M^H ^ t-x), (1) где t — время с момента возбуждения.

При сварке поверхности углового шва и раздела зон ориентированы преимущественно в плоскости, соединяющей катеты углового шва. Такие поверхности удобно описывать как отклонение от этой плоскости. Поэтому координата z направлена по биссектрисе а угла между листами (или угла разделки кромок).

Теплоперенос является общим процессом для всех выделенных зон . При моделировании рассматривается термодинамическое состояние сред с разными теплофизическими свойствами, в которых действуют несколько внутренних объемно распределенных источников теплоты. Скорость изменения и распределение энтальпии следует описывать уравнением [10]:

д^А^дП+А^дП + А^^ х y _Z/1). (2) dt дх V дх) ду V ду/ dz V dz/ ^{4 4 J J v} ’

Здесь H = H ( x , y , z , t ) — объемная энтальпия, Дж/см ³ ; Z = Z( Т ) — коэффициент теплопроводности, зависящий от температуры и материала среды, Вт/(см^°С); q — объемный источник теплоты. Температура T ( x , y , z , t ) связана с энтальпией H ( x , y , z , t ) нелинейной функцией T ( H ), учитывающей зависимость теплоемкости от температуры и теплоты фазовых и агрегатных превращений. В начальный момент времени сварочная ванна отсутствует, флюс находится в сыпучем состоянии, температура во всех точках пространства одинакова и равна температуре окружающей среды. С учетом этого теплообмен зоны моделирования с внешним пространством

можно описать граничными условиями:

g=0, x =±х т ,                               (3) 2 ^=0, у =±У т ,                               (4) У2=0, Z =±z m .                                        (5)

Источники теплоты. Основные источники теплоты: электрическая дуга qarc, действующая в зоне D, и теплота, выделяемая при вылете электрода [11, 12]. Тепловыделение в жидком флюсе практически отсутствует, так как он не имеет прямого контакта с электродом, температура которого меньше температуры плавления флюса, а электрическое сопротивление порошкового флюса очень велико. С учетом этих обстоятельств скорость нагревания металла в вылете электрода (в зоне E) можно описать соотношением:

dry _ р_ер z_m-z dz     cp y V y

4/ ⁿd 2 _f

плотность тока I в

где Tj — температура вылета; рe = рe(Tf) — удельное электрическое сопротивление; j = электроде диаметром dj; срf — объемная теплоемкость материала электрода; vj — скорость подачи электродной проволоки.

Тепловыделение в анодной области дуги на поверхности E n D описано как тепловой поток:

Z=u,(7)

где U_a — падение напряжения в анодной области дуги.

Тепловыделение в плазменном факеле дуги учтено как распределение излучения столба дуги по поверхности дуговой каверны L n ( D и V ):

g2=0,y = ±y„,.(8)

Тепловой поток, создаваемый тепловыделением в катодной области дуги на поверхности L n D , равен:

2 = U2ex₽(=5#)

где U k — катодное напряжение дуги, R — эффективный радиус дуги, r ₀ — расстояние между точкой поверхности L n D и точкой пересечения оси дуги с этой поверхностью.

Теплоперенос каплями электродного металла учитывается тепловым потоком через поверхность L n D [13]:

q = 22LexX)(-!i dn nR2 exp ( R2 )

где Tk — температура капель, принятая равной полусумме температур плавления и кипения материала электрода.

Теплопередача парами флюса описана как тепловой поток через поверхность сварочной ванны Ln V и а2т флюса Gn V: — = 0, z = ±zm. Коэффициент теплопередачи определяется из баланса мощностей испарения и конденсации пара:

J ₇ q ^dS z Р vap^va^^{0 ,                                 (11)}

Z dn где Sz — площадь указанных поверхностей Ln VоGn V.

Уравнение равновесия поверхности сварочной ванны. Расположение поверхности сварочной ванны

Z ( x , у ), разграничивающей зоны L n ( D о V и G ), определено решением уравнения равновесия давлений на ней: — капиллярного p _а,

— гравитационного P g ,

— потока капель электродного металла p f ,

— гидродинамического давления потока металла сварочной ванны p_v ,

— электродинамического давления дуги P a ,

— внутреннего давления жидкого металла p m . ^dT/ _ РеР z_m-z dz = cp_f  v_f .

Капиллярное давление определяется кривизной поверхности Z ( x , у ) и при малых прогибах вычисляется:

(a2z , a2z\

^{P a} = ^-а ЛЛ ⁺ аЛ)’

где о — коэффициент поверхностного натяжения.

Гравитационное давление определяется весом столба вещества над точкой поверхности сварочной

ванны:

P g = g(^p(Z - ^z max ) + P h^ )’                                     ⁽¹⁴⁾

где g — ускорение свободного падения; p, p h — плотности металла и шлака; z_max — максимальная высота поверхности сварочной ванны; Z h — толщина слоя жидкого шлака.

Электродинамическое давление сварочной дуги определяется током дуги:

P ^ ■ pl ' У + |                                      (15)

nRp             Rp где ka — электродинамический коэффициент, Rp — силовой радиус дуги.

Давление потока капель электродного металла определяется скоростью и массой потока:

У Т       ^- Cr o ^+v w t ⁾²⁺ y ²

Pf = Р 2 exp [     R2      J .

Гидродинамическое давление потока металла сварочной ванны определяется темпом изменения площади сечения сварочной ванны S L :

dS

Pv = -PV 2-^.

Эта составляющая увеличивает давление перед дугой и уменьшает позади дуги.

Внутреннее давление в расплаве p m определяется из равенства площади наплавленного металла количеству израсходованного металла электрода:

SsuM(-Xm) - SM(+Xm)Pm = vrП ff ^,(18)

где ^им(-^т) — площадь поперечного сечения металла в конце области моделирования при x = -xm; 5м 00 — начальная площадь поперечного сечения разделки кромок при x = xm.

Ток и расположение сварочной дуги. Ток сварочной дуги I задается скоростью подачи V f и диаметром d f электрода:

I = v' ^ d-^c p _f (T _k - T _f )+ H_LS ),                                  (19)

где T_k — температура капель электродного металла; H_LS — объемная удельная теплота плавления.

Длина l сварочной дуги задается напряжением U ₀ источника питания и зависит от электрического сопротивления токоведущих элементов R 0 и вылета электрода R f :

l = 1/ E ( U о - U a - U k -1 ( R o + Rf- )).                                      (20)

Длина дуги определяется градиентом потенциала E в столбе дуги, значение которого зависит от свойств пара флюса. При криволинейной поверхности LnD катодного пятна понятие длины дуги нуждается в уточнении. Если рассматривать столб дуги как множество параллельных проводников, то плотность тока будет тем больше, чем меньше расстояние от конца электрода до точки поверхности металла. Среднюю длину l множества таких проводников можно определить решением уравнения:

1-jS^ dS = - .

-у s ^J0 г²         I

Машиностроение и машиноведение

Здесь r — расстояние от конца электрода до рассматриваемой точки поверхности сварочной ванны; S — площадь сечения столба, определяемая эффективным радиусом R дуги. Последний зависит от тока I дуги [13]:

'■■■ 2• где j — плотность тока в дуге в парах флюса.

Электрическое сопротивление вылета зависит от его длины L f и температуры T f , распределенной по длине:

R _f = n d- 2 S ^L _Q^fP e (T _f (z)dz).                                       (22)

Алгоритм численного решения системы уравнений физико-математической модели. Изначально неизвестно геометрическое строение зоны формирования сварочной ванны. Это требует непрерывной корректировки расположения межзонных поверхностей в зависимости от результатов решения уравнений теплопроводности и равновесия сварочной ванны. Расположение поверхностей, разграничивающих твердое, жидкое и газообразное состояние флюса и металла, уточняется по положению соответствующих изотерм в результате решения уравнения теплопроводности. Для корректировки расположения поверхности сварочной ванны решается уравнение равновесия давлений на данной поверхности Z ( x , у ). В этом случае необходимо изменить размеры зон L , V , G , D . Принимается, что температуры металла и шлака в зоне перемещения равны температуре поверхности на момент выполнения решения, а их энтальпии изменяются в соответствии с этой температурой. При трансформации возникают погрешности, которые определяются как скорости изменения энтальпии при изменении объемов v_L , v_G зон L и G :

al=    d ) и Л       d)(23)

Эти погрешности компенсируются изменением энтальпии зон L и G в зависимости от распределения в них температуры:

• -H((x,y z)EL) = Al , r T(x'y^-П----,(24)

• dt            1     yJ^X,y,z)-TlWl’

где T L — температура ликвидуса.

По мере приближения термодинамического состояния к установившемуся состоянию погрешность трансформации Л _L ^0. Условием окончания моделирования является стабилизация длины изотермы солидуса:

— (maxx Е 5) ^ 0.(25)

Система уравнений модели решается распределением температуры T ( x , у , z , t ) и геометрического строения зоны моделирования. Это позволяет воспроизвести начальную стадию процесса с момента возбуждения дуги до достижения установившихся размеров сварочной ванны . Для решения уравнений теплопроводности и равновесия поверхности сварочной ванны использован метод конечных разностей на сопряженных сетках. На межфазных поверхностях коэффициент теплопроводности определяли как среднегармоническое значение теплопроводности соседних фаз.

Ниже схематично представлен алгоритм численного моделирования процесса сварки.

Исходные данные: геометрия разделки кромок после выполнения предшествующего прохода, теплофизические свойства стали и флюса, параметры сварки

Определение начальной геометрии области численного решения

Расчет параметров плавления электродной проволоки и энергетических характеристик сварочной дуги

Цикл нестационарного численного моделирования термодинамического состояния области формирования сварочной ванны

Определение распределения тепловых потоков по поверхностям металла и шлака

Решение уравнения теплопроводности

Решение вариационной задачи о расположении сварочной дуги в разделке кромок

Решение уравнения равновесия поверхности сварочной ванны при воздействии капиллярного, гравитационного, электродинамического, гидродинамического и внутреннего давлений

Расчет внутреннего давления сварочной ванны по условию баланса масс шва и подачи электрода до равенства масс наплавки и подачи электрода

Корректировка расположения межфазовых границ «пар — шлак — сыпучий флюс — твердый шлак», «твердый — жидкий металл» по решениям уравнения теплопроводности и равновесия поверхности сварочной ванны до стабилизации длины изотермы температуры солидуса

Формирование протокола результатов моделирования по распределению температур, геометрии области формирования сварочной ванны, энергетических характеристик процесса сварки

Рис. 2. Алгоритм численного моделирования формирования шва при дуговой сварке под флюсом

Результаты исследования. Для виртуального исследования взяли сведения о теплофизических свойствах сталей из [13]. Кроме того, использовали данные группы компаний «Трансстрой» о конкретных применяемых марках сталей и технологических материалах, режимах сварки под флюсом угловых швов мостовых металлоконструкций 1 .

Виртуальное воспроизведение процесса сварки « в лодочку ». Для проверки разработанной модели выполнили компьютерное моделирование процесса сварки таврового соединения Т1 листов из стали 15ХСНД толщиной 12 мм. Режим сварки выбрали в соответствии с рекомендациями [14]: проволока Св08ГА диаметром 5 мм, напряжение дуги — 34 В, скорость сварки — 18 м/час (5 мм/с), вылет электрода — 25 мм. Скорость подачи электрода, рассчитанная в модели, — 10 мм/с, что соответствует данным работы [14], рекомендующей эти значения в диапазоне 55–61 м/час.

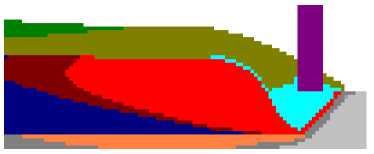
На рис. 3 представлены результаты моделирования процесса сварки при наклоне листов 45о (в

«лодочку»).

а )

б )

в )

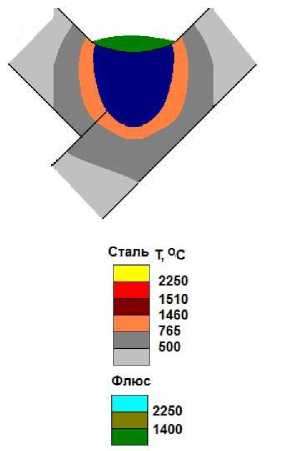
г )

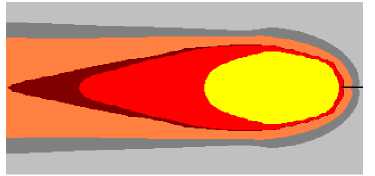
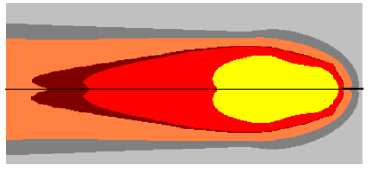
Рис. 3. Распределение температуры при моделировании процесса сварки углового шва под флюсом при наклоне листов 45^о (в «лодочку»): а ― продольное сечение сварочной ванны в плоскости симметрии стыка ; б ― поверхность металла под флюсом; в ― поверхность свариваемых листов; г ― расчетный профиль поперечного сечения шва

В результате получены значения: длина дуги — 6,8 мм; эффективное падение анодного напряжения — 5,9 В, катодного — 8,5 В; градиент потенциала в столбе дуги — 4,4 В/мм; диаметр столба дуги — 18 мм. Общая мощность процесса — 23 кВт, из нее на излучение приходится 12,9 кВт. Дуга выделяет на электроде 4,3 кВт; на поверхности стыка — 5,8 кВт. Мощность тепловыделения в вылете электрода — 0,2 кВт; температура его нагрева током дуги — 152 ^оС. Площадь плана дуговой каверны — 135 мм 2 ; объем каверны — 519 мм 3 . Глубина кратера под дугой — 16 мм. Длина сварочной ванны на поверхности по ликвидусу — 38 мм, по солидусу — 52 мм. Масса сварочной ванны — 150 г. Ширина шва — 15 мм; катет — 10,7 мм; глубина проплавления стыка — 6 мм; площадь поперечного сечения — 158 мм 2 . Шов формируется с мениском до 1,3 мм.

Виртуальное воспроизведение процесса сварки «в угол». При сварке конструкций большого размера невозможно использовать кантователи. В этом случае выполняется сварка «в угол». Результат моделирования формирования шва при таком положении и тех же условиях показан на рис. 4.

Машиностроение и машиноведение

1 СТО - ГК «Трансстрой» -012- 2007. Стальные конструкции мостов. Заводское изготовление / Трансстрой. М., 2007. 174 с.

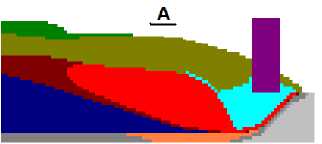
а )

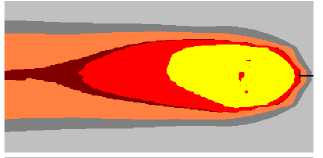
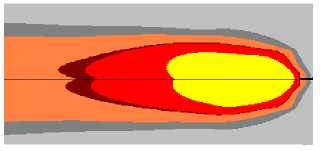
в )

б )

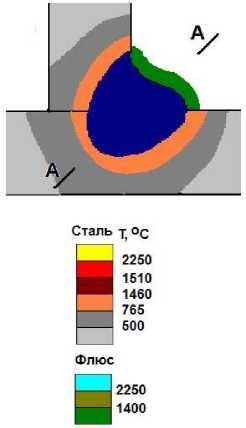
Рис. 4. Результат компьютерного моделирования формирования углового шва при сварке «в угол» с приваркой вертикальной стенки к горизонтальному основанию: а — продольное сечение сварочной ванны в плоскости симметрии стыка; б — поверхность металла под флюсом; в — поверхность свариваемых листов;

г — расчетный профиль поперечного сечения шва

Заметное стекание расплава со стенки стыка на полку при сварке «в угол» обусловлено большой массой сварочной ванны. Отклонение поверхности шва от плоскости, соединяющей стенки, — ±1,5 мм. Расплав стекает с вертикальной стенки на горизонтальное основание, поэтому сварной шов получается асимметричным, а расплав в верхней части шва уменьшается на 2 мм.

Максимально возможный размер катета. Необходимо выяснить, при каком максимальном размере катета (сварка «в лодочку» и «в угол») формируется качественный шов. С этой целью выполнили моделирование сварки углового шва листов толщиной 8 мм проволокой диаметром 2 мм при токе дуги 350 А. Варьировали скорость сварки и напряжение дуги. Результаты представлены на рис. 5.

б )

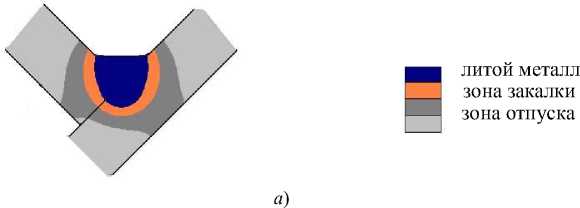
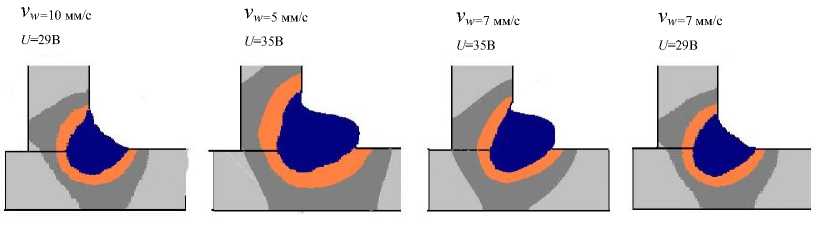
Рис. 5. Результат компьютерного моделирования формирования шва: а — «в лодочку», б — «в угол»

Если соблюдать рекомендуемую в работе скорость сварки «в лодочку» (рис. 5 а ), формируется шов с равными катетами 6 мм. Это меньше требуемого, но без наплыва и мениска. При сварке «в угол» на том же режиме (рис. 5 б ) формируется шов с мениском. Для увеличения катета выполнили моделирование при меньшей скорости сварки и большем значении напряжения дуги. При скорости 5 мм/с и напряжении 35 В площадь сечения литой зоны и ее размеры существенно увеличиваются, но формируется шов с подрезом и натеком. Увеличение скорости сварки до 7 мм/с уменьшает натек. Если снизить напряжение, приемлемый шов формируется при катетах около 7 мм.

Эти результаты показывают, что рекомендуемые режимы сварки под флюсом являются наиболее производительными для получения катетов заданных размеров. Для получения катетов большего размера при однодуговой сварке необходимы дополнительные проходы. Однако общая производительность сварки в этом случае значительно снижается.

Обсуждение и заключение. Трудоемкость изготовления элементов мостовых конструкций в значительной мере определяется трудоемкостью сварки. Рациональным способом повышения производительности является использование автоматической сварки под флюсом. Для оптимизации технологии методами компьютерного анализа разработана физико-математическая модель формообразования угловых швов при сварке под флюсом. Основа модели — система уравнений теплопроводности и равновесия поверхности сварочной ванны. В данной системе формирование дуговой каверны определено по изотерме кипения флюса под действием излучения столба дуги. Учтены теплоперенос парами флюса внутри дуговой каверны и влияние пространственного положения на формирование сварочной ванны. Численно решены уравнения модели сварки под флюсом углового соединения при толщине металла, типичной для мостовых конструкций. Решение показало, что при выполнении сварки «в лодочку» соединение формируется в один проход. По данным моделирования, при сварке углового шва «в угол» возможно неудовлетворительное формирование из-за стекания жидкого металла с вертикальной стенки. В этом случае для получения качественного шва необходимы дополнительные подварочные проходы.

Исследования показали, что традиционная технология однодуговой сварки под флюсом угловых швов с формированием катетов увеличенного размера уже достигла своей максимальной производительности. Для дальнейшего ее повышения необходимо использовать более сложные специальные приемы. Среди таких нетрадиционных технологий:

— многодуговые и многоэлектродные способы сварки [14, 15],

— введение в сварочную ванну нетоковедущей (холодной) присадочной проволоки [16], гранулированной металлической присадки (крупки) или металлического порошка [17].